求解思路：

中缀表达式转成后缀表达式，根据后缀表示式生成二叉表达式数，在根据上树生成导函数树。牛顿迭代法求解一元多次方程

牛顿迭代法：

http://www.devacg.com/?post=351
一元非线性方程的求解是高等数学研究的重要课题之一，早在2000多年前，古巴比伦的数学家就能解一元二次方程了，中国的《九章算术》也有对一元二次方程求解的记载。目前人们普遍认为低阶（5阶以下）元非线性方程可以通过求根公式求解，但是高于或等于5阶的一元非线性方程不存在求根公式，要精确求解非常困难。对高阶方程，一般采用迭代法近似求解，牛顿迭代法因为方法简单，迭代收敛速度快而被广泛使用。

牛顿迭代法（Newton’s method）又称牛顿-拉弗森方法（Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数（x）的泰勒级数的前面几项来寻找方程（x）-0的根。
牛顿迭代法逼近示意图：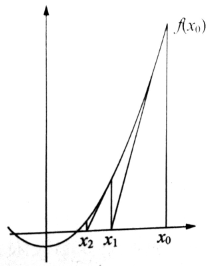
求解一元多次方程 - 图1
首先，选择一个接近函数（x）零点的x0作为迭代初始值，计算相应的（x0）和切线斜率（xO）（这里（x）是函数（x）的一阶导函数）。然后我们经过点（xO，f（x））做一条斜率为f（x0）的直线，该直线与x轴有一个交点，可通过以下方程的求解得到这个交点的x坐标：

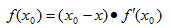
求解一元多次方程 - 图2

求解这个方程，可以得到：

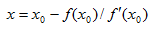
求解一元多次方程 - 图3

我们将新求得的点的x坐标命名为x1，通常x1会比x0更接近方程（X）-0的解。因此我们现在可以利用x1开始下一轮迭代。根据上述方程中x1和x0的关系，可以得到一个求解x的迭代公式：

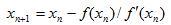
求解一元多次方程 - 图4

这就是牛顿迭代公式。目前已经证明，如果（x）的一阶导函数（x）是连续函数，并且待求的零点x是孤立的，则在零点x周围存在一个区间，只要初始值x0位于这个区间，牛顿迭代必定收敛。并且，只要（x）0，牛顿送代法具有平方收敛的性能。这意味着每迭代一次，结果的有效数字将增加一倍，这比二分逼近法的线性收敛速度快了一个数量级。

导函数的求解与近似公式

  1. using System;
  3. namespace NewtonTest
  4. {
  5.     class Program
  6.     {
  7.         public delegate double Function(double x);
  8.         const double PRECISION = 0.1;//计算精度
  10.         static void Main(string[] args)
  11.         {
  12.             double x = NewtonRaphson(TestFun, -8);
  13.             Console.WriteLine("f({0})={1}", x, TestFun(x));
  14.             Console.Read();
  16.         }
  18.         //示例方程：一元二次方程
  19.         //求解y=0时,x的值.
  20.         public static double TestFun(double x)
  21.         {
  22.             //注意：要确保这个方程是有解的。
  23.             double y = 5 * Math.Pow(x, 2) + 8 * x + 2;
  24.             return y;
  25.         }
  27.         /// <summary>
  28.         /// 计算函数f在x附近的一阶导数值
  29.         /// </summary>
  30.         /// <param name="f">原函数</param>
  31.         /// <param name="x">x值</param>
  32.         /// <returns></returns>
  33.         public static double CalcDerivative(Function f, double x)
  34.         {
  35.             return (f(x + 0.000005) - f(x - 0.000005))/0.00001;
  36.         }
  38.         /// <summary>
  39.         /// 牛顿迭代法
  40.         /// 用于求解一元非线性方程
  41.         /// </summary>
  42.         /// <param name="f">原函数</param>
  43.         /// <param name="x0">迭代初始值</param>
  44.         /// <returns></returns>
  45.         public static double NewtonRaphson(Function f, double x0)
  46.         {
  47.             double x1 = x0 - f(x0) / CalcDerivative(f, x0);
  48.             while(Math.Abs(x1 - x0) > PRECISION)
  49.             {
  50.                 x0 = x1;
  51.                 x1 = x0 - f(x0) / CalcDerivative(f, x0);
  52.             }
  53.             return x1;
  54.         }
  55.     }
  56. }

中缀表达式转后缀表达式—C#代码实现

https://blog.csdn.net/Czhenya/article/details/78067542
版主没用递归来实现，有些繁琐

  1. namespace 玩嗨的练习
  2.     {
  3.         class Program
  4.         {
  5.             static void Main(string[] args)
  6.             {
  7.                 //运行时用建议输入空格
  8.                 Console.WriteLine("请输入您要转换的表达式：");
  9.                 string inputstr = Console.ReadLine();
  10.                 //测试用
  11.                 //string inputstr = "9 * (3 - 1) + (10 - 1) / 2";
  12.                 //string inputstr = "1 - 2 - 3 * 4 + 10 / 5";
  13.                 Console.WriteLine("您转换后的结果为：");
  14.                 Change(inputstr);
  16.                 Console.ReadKey();
  17.             }
  19.             private static void Change(string inputstr)
  20.             {
  21.                 Stack<char> arrStark = new Stack<char>();
  23.                 char[] arrChar = inputstr.ToCharArray();
  26.                 int a = 4;  //默认状态是什么都没有,这里是4状态，，
  28.                 for (int i = 0; i < arrChar.Length; i++)
  29.                 {
  30.                     //数字空格就直接输出
  31.                     if (arrChar[i] <= '9' && arrChar[i] >= '0')
  32.                     {
  33.                         Console.Write(arrChar[i]);
  34.                     }
  35.                     if (arrChar[i] == ' ')
  36.                     {
  37.                         Console.Write(" ");
  38.                     }
  40.                     //运算符走状态机
  41.                     switch (a)
  42.                     {
  43.                         //=============================状态1 * / ====================================
  44.                         case 1:  //表示当前是+- 状态
  45.                             if (arrChar[i] == '+' || arrChar[i] == '-')
  46.                             {
  47.                                 a = 1;
  48.                                 Console.Write(arrStark.Pop());
  49.                                 arrStark.Push(arrChar[i]);
  50.                             }
  51.                             else
  52.                             if (arrChar[i] == '*' || arrChar[i] == '/')
  53.                             {
  54.                                 a = 2;
  55.                                 arrStark.Push(arrChar[i]);
  56.                             }
  57.                             else
  58.                             if (arrChar[i] == '(')
  59.                             {
  60.                                 a = 3;
  61.                                 arrStark.Push(arrChar[i]);
  62.                             }
  63.                             else
  64.                             if (arrChar[i] == ')')
  65.                             {
  66.                                 a = 4;
  67.                                 for (int j = 0; j < arrStark.Count; j++)
  68.                                 {
  69.                                     //输出括号中间的符号，，，
  70.                                     if (arrStark.Peek() == '(')
  71.                                     {
  72.                                         //把左括号，，弹出栈外
  73.                                         arrStark.Pop();
  74.                                         break;
  75.                                     }
  76.                                     else
  77.                                     {
  78.                                         Console.Write(arrStark.Pop());
  79.                                     }
  80.                                 }
  81.                             }
  82.                             break;
  83.                         //=============================状态2 * / ====================================
  84.                         case 2:  //表示当前是* / 状态
  85.                             if (arrChar[i] == '+' || arrChar[i] == '-')
  86.                             {
  87.                                 a = 1;
  88.                                 for (int j = 0; j <= arrStark.Count; j++)
  89.                                 {
  90.                                    //Console.Write(arrStark.Count);
  91.                                    Console.Write(arrStark.Pop());
  92.                                 }
  93.                                 arrStark.Push(arrChar[i]);
  94.                             }
  95.                             else
  96.                             if (arrChar[i] == '*' || arrChar[i] == '/')
  97.                             {
  98.                                 a = 2;
  99.                                 Console.Write(arrStark.Pop());
  100.                                 arrStark.Push(arrChar[i]);
  101.                             }
  102.                             else
  103.                             if (arrChar[i] == '(')
  104.                             {
  105.                                 a = 3;
  106.                                 arrStark.Push(arrChar[i]);
  107.                             }
  108.                             else
  109.                             if (arrChar[i] == ')')
  110.                             {
  111.                                 a = 4;
  112.                                 for (int j = 0; j < arrStark.Count; j++)
  113.                                 {
  114.                                     if (arrStark.Peek() == '(')
  115.                                     {
  116.                                         //把左括号，，弹出栈外
  117.                                         arrStark.Pop();
  118.                                         break;
  119.                                     }
  120.                                     else
  121.                                     {
  122.                                         //输出括号中间的符号，，，
  123.                                         Console.Write(arrStark.Pop());
  124.                                     }
  125.                                 }
  126.                             }
  127.                             break;
  128.                         //=============================状态3 ） ====================================
  129.                         case 3:  //表示当前是( 状态
  130.                             if (arrChar[i] == '+' || arrChar[i] == '-')
  131.                             {
  132.                                 arrStark.Push(arrChar[i]);
  133.                             }
  134.                             else
  135.                             if (arrChar[i] == '*' || arrChar[i] == '/')
  136.                             {
  137.                                 arrStark.Push(arrChar[i]);
  138.                             }
  139.                             else
  140.                             if (arrChar[i] == '(')
  141.                             {
  142.                                 a = 3;
  143.                                 arrStark.Push(arrChar[i]);
  144.                             }
  145.                             else
  146.                             if (arrChar[i] == ')')
  147.                             {
  148.                                 a = 4;
  149.                                 for (int j = 0; j < arrStark.Count; j++)
  150.                                 {
  151.                                     if (arrStark.Peek() == '(')
  152.                                     {
  153.                                         //把左括号，，弹出栈外
  154.                                         arrStark.Pop();
  155.                                         break;
  156.                                     }
  157.                                     else
  158.                                     {
  159.                                         //输出括号中间的符号，，，
  160.                                         Console.Write(arrStark.Pop());
  161.                                     }
  162.                                 }
  163.                             }
  164.                             break;
  165.                         //=============================状态4 （ ====================================
  166.                         case 4:  //表示当前是 )  状态
  167.                             if (arrChar[i] == '+' || arrChar[i] == '-')
  168.                             {
  169.                                 if (arrStark.Count == 0)
  170.                                 {
  171.                                     a = 1;
  172.                                     arrStark.Push(arrChar[i]);
  173.                                 }
  174.                                 else
  175.                                 {
  176.                                     if (arrStark.Peek() == '+' || arrStark.Peek() == '-')
  177.                                     {
  178.                                         a = 1;
  179.                                         arrStark.Push(arrChar[i]);
  180.                                     }
  181.                                     else
  182.                                     if (arrStark.Peek() == '*' || arrStark.Peek() == '/')
  183.                                     {
  184.                                         a = 1;
  185.                                         for (int j = 0; j < arrStark.Count; j++)
  186.                                         {
  187.                                             Console.Write(arrStark.Pop());
  188.                                         }
  189.                                         arrStark.Push(arrChar[i]);
  191.                                     }
  192.                                 }
  193.                             }
  194.                             else
  195.                             if (arrChar[i] == '*' || arrChar[i] == '/')
  196.                             {
  197.                                 if (arrStark.Count == 0)
  198.                                 {
  199.                                     a = 2;
  200.                                     arrStark.Push(arrChar[i]);
  201.                                 }
  202.                                 else
  203.                                 {
  204.                                     if (arrStark.Peek() == '+' || arrStark.Peek() == '-')
  205.                                     {
  206.                                         a = 2;
  207.                                         arrStark.Push(arrChar[i]);
  209.                                     }
  210.                                     else if (arrStark.Peek() == '*' || arrStark.Peek() == '/')
  211.                                     {
  212.                                         a = 2;
  213.                                         arrStark.Push(arrChar[i]);
  215.                                     }
  216.                                 }
  217.                             }
  218.                             else
  219.                             if (arrChar[i] == '(')
  220.                             {
  221.                                 a = 3;
  222.                                 arrStark.Push(arrChar[i]);
  223.                             }
  224.                             if (arrChar[i] == ')')
  225.                             {
  226.                                 a = 4;
  227.                                 for (int j = 0; j < arrStark.Count; j++)
  228.                                 {
  229.                                     if (arrStark.Peek() == '(')
  230.                                     {
  231.                                         //把左括号，，弹出栈外
  232.                                         arrStark.Pop();
  233.                                         break;
  234.                                     }
  235.                                     else
  236.                                     {
  237.                                         //输出括号中间的符号，，，
  238.                                         Console.Write(arrStark.Pop());
  239.                                     }
  240.                                 }
  241.                             }
  242.                             break;
  243.                         default:
  244.                             Console.WriteLine("Wrong");
  245.                             break;
  247.                     }
  248.                 }
  249.                 //遍历栈中剩余的符号输出，并清空栈，
  250.                 foreach (char item in arrStark)
  251.                 {
  252.                     Console.Write(" " + item);
  253.                 }
  254.                 arrStark.Clear();
  256.             }
  258.       }
  259. }
  260. ————————————————
  261. 版权声明：本文为CSDN博主「Czhenya」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
  262. 原文链接：https://blog.csdn.net/Czhenya/article/details/78067542

表达式树及其实现

https://www.chaoswork.cn/904.html