1 超参数
1.1 什么是超参数,参数和超参数的区别?
区分两者最大的一点就是是否通过数据来进行调整,模型参数通常是有数据来驱动调整,超参数则不需要数据来驱动,而是在训练前或者训练中人为的进行调整的参数。例如卷积核的具体核参数就是指模型参数,这是有数据驱动的。而学习率则是人为来进行调整的超参数。这里需要注意的是,通常情况下卷积核数量、卷积核尺寸这些也是超参数,注意与卷积核的核参数区分。
1.2 神经网络中包含哪些超参数?
通常可以将超参数分为三类:网络参数、优化参数、正则化参数。
网络参数:可指网络层与层之间的交互方式(相加、相乘或者串接等)、卷积核数量和卷积核尺寸、网络层数(也称深度)和激活函数等。
优化参数:一般指学习率(learning rate)、批样本数量(batch size)、不同优化器的参数以及部分损失函数的可调参数。
正则化:权重衰减系数,丢弃法比率(dropout)
1.3 为什么要进行超参数调优?
本质上,这是模型优化寻找最优解和正则项之间的关系。网络模型优化调整的目的是为了寻找到全局最优解(或者相比更好的局部最优解),而正则项又希望模型尽量拟合到最优。两者通常情况下,存在一定的对立,但两者的目标是一致的,即最小化期望风险。模型优化希望最小化经验风险,而容易陷入过拟合,正则项用来约束模型复杂度。所以如何平衡两者之间的关系,得到最优或者较优的解就是超参数调整优化的目的。
1.4 超参数的重要性顺序
- 首先, 学习率,损失函数上的可调参数。在网络参数、优化参数、正则化参数中最重要的超参数可能就是学习率了。学习率直接控制着训练中网络梯度更新的量级,直接影响着模型的有效容限能力;损失函数上的可调参数,这些参数通常情况下需要结合实际的损失函数来调整,大部分情况下这些参数也能很直接的影响到模型的的有效容限能力。这些损失一般可分成三类,第一类辅助损失结合常见的损失函数,起到辅助优化特征表达的作用。例如度量学习中的Center loss,通常结合交叉熵损失伴随一个权重完成一些特定的任务。这种情况下一般建议辅助损失值不高于或者不低于交叉熵损失值的两个数量级;第二类,多任务模型的多个损失函数,每个损失函数之间或独立或相关,用于各自任务,这种情况取决于任务之间本身的相关性,目前笔者并没有一个普适的经验由于提供参考;第三类,独立损失函数,这类损失通常会在特定的任务有显著性的效果。例如RetinaNet中的focal loss,其中的参数γ,α,对最终的效果会产生较大的影响。这类损失通常论文中会给出特定的建议值。
- 其次,批样本数量,动量优化器(Gradient Descent with Momentum)的动量参数β。批样本决定了数量梯度下降的方向。过小的批数量,极端情况下,例如batch size为1,即每个样本都去修正一次梯度方向,样本之间的差异越大越难以收敛。若网络中存在批归一化(batchnorm),batch size过小则更难以收敛,甚至垮掉。这是因为数据样本越少,统计量越不具有代表性,噪声也相应的增加。而过大的batch size,会使得梯度方向基本稳定,容易陷入局部最优解,降低精度。一般参考范围会取在[1:1024]之间,当然这个不是绝对的,需要结合具体场景和样本情况;动量衰减参数β是计算梯度的指数加权平均数,并利用该值来更新参数,设置为 0.9 是一个常见且效果不错的选择;
- 最后,Adam优化器的超参数、权重衰减系数、丢弃法比率(dropout)和网络参数。在这里说明下,这些参数重要性放在最后并不等价于这些参数不重要。而是表示这些参数在大部分实践中不建议过多尝试,例如Adam优化器中的β1,β2,ϵ,常设为 0.9、0.999、10−8就会有不错的表现。权重衰减系数通常会有个建议值,例如0.0005 ,使用建议值即可,不必过多尝试。dropout通常会在全连接层之间使用防止过拟合,建议比率控制在[0.2,0.5]之间。使用dropout时需要特别注意两点:一、在RNN中,如果直接放在memory cell中,循环会放大噪声,扰乱学习。一般会建议放在输入和输出层;二、不建议dropout后直接跟上batchnorm,dropout很可能影响batchnorm计算统计量,导致方差偏移,这种情况下会使得推理阶段出现模型完全垮掉的极端情况;网络参数通常也属于超参数的范围内,通常情况下增加网络层数能增加模型的容限能力,但模型真正有效的容限能力还和样本数量和质量、层之间的关系等有关,所以一般情况下会选择先固定网络层数,调优到一定阶段或者有大量的硬件资源支持可以在网络深度上进行进一步调整。
1.5 部分超参数如何影响模型性能?
| 超参数 | 如何影响模型容量 | 原因 | 注意事项 | | —- | —- | —- | —- | | 学习率 | 调至最优,提升有效容量 | 过高或者过低的学习率,都会由于优化失败而导致降低模型有效容限 | 学习率最优点,在训练的不同时间点都可能变化,所以需要一套有效的学习率衰减策略 | | 损失函数部分超参数 | 调至最优,提升有效容量 | 损失函数超参数大部分情况都会可能影响优化,不合适的超参数会使即便是对目标优化非常合适的损失函数同样难以优化模型,降低模型有效容限。 | 对于部分损失函数超参数其变化会对结果十分敏感,而有些则并不会太影响。在调整时,建议参考论文的推荐值,并在该推荐值数量级上进行最大最小值调试该参数对结果的影响。 | | 批样本数量 | 过大过小,容易降低有效容量 | 大部分情况下,选择适合自身硬件容量的批样本数量,并不会对模型容限造成。 | 在一些特殊的目标函数的设计中,如何选择样本是很可能影响到模型的有效容限的,例如度量学习(metric learning)中的N-pair loss。这类损失因为需要样本的多样性,可能会依赖于批样本数量。 | | 丢弃法 | 比率降低会提升模型的容量 | 较少的丢弃参数意味着模型参数量的提升,参数间适应性提升,模型容量提升,但不一定能提升模型有效容限 | | | 权重衰减系数 | 调至最优,提升有效容量 | 权重衰减可以有效的起到限制参数变化的幅度,起到一定的正则作用 | | | 优化器动量 | 调至最优,可能提升有效容量 | 动量参数通常用来加快训练,同时更容易跳出极值点,避免陷入局部最优解。 | | | 模型深度 | 同条件下,深度增加,模型容量提升 | 同条件,下增加深度意味着模型具有更多的参数,更强的拟合能力。 | 同条件下,深度越深意味着参数越多,需要的时间和硬件资源也越高。 | | 卷积核尺寸 | 尺寸增加,模型容量提升 | 增加卷积核尺寸意味着参数量的增加,同条件下,模型参数也相应的增加。 | |
1.6 部分超参数合适的范围
| 超参数 | 建议范围 | 注意事项 |
|---|---|---|
| 初始学习率 | SGD: [1e-2, 1e-1] momentum: [1e-3, 1e-2] Adagrad: [1e-3, 1e-2] Adadelta: [1e-2, 1e-1] RMSprop: [1e-3, 1e-2] Adam: [1e-3, 1e-2] Adamax: [1e-3, 1e-2] Nadam: [1e-3, 1e-2] |
这些范围通常是指从头开始训练的情况。若是微调,初始学习率可在降低一到两个数量级。 |
| 损失函数部分超参数 | 多个损失函数之间,损失值之间尽量相近,不建议超过或者低于两个数量级 | 这是指多个损失组合的情况,不一定完全正确。单个损失超参数需结合实际情况。 |
| 批样本数量 | [1:1024] | 当批样本数量过大(大于6000)或者等于1时,需要注意学习策略或者内部归一化方式的调整。 |
| 丢弃法比率 | [0, 0.5] | |
| 权重衰减系数 | [0, 1e-4] | |
| 卷积核尺寸 | [7x7],[5x5],[3x3],[1x1], [7x1,1x7] |
1.7 网络训练中的超参调整策略
1.7.1 如何调试模型?
在讨论如何调试模型之前,我们先来纠正一个误区。通常理解如何调试模型的时候,我们想到一系列优秀的神经网络模型以及调试技巧。但这里需要指出的是数据才是模型的根本,如果有一批质量优秀的数据,或者说你能将数据质量处理的很好的时候,往往比挑选或者设计模型的收益来的更大。那在这之后才是模型的设计和挑选以及训练技巧上的事情。
1、探索和清洗数据。探索数据集是设计算法之前最为重要的一步,以图像分类为例,我们需要重点知道给定的数据集样本类别和各类别样本数量是否平衡,图像之间是否存在跨域问题(例如网上爬取的图像通常质量各异,存在噪声)。若是类别数远远超过类别样本数(比如类别10000,每个类别却只有10张图像),那通常的方法可能效果并不显著,这时候few-shot learning或者对数据集做进一步增强可能是你比较不错的选择。再如目标检测,待检测目标在数据集中的尺度范围是对检测器的性能有很大影响的部分。因此重点是检测大目标还是小目标、目标是否密集完全取决于数据集本身。所以,探索和进一步清洗数据集一直都是深度学习中最重要的一步。这是很多新手通常会忽略的一点。
2、探索模型结果。探索模型的结果,通常是需要对模型在验证集上的性能进行进一步的分析,这是如何进一步提升模型性能很重要的步骤。将模型在训练集和验证集都进行结果的验证和可视化,可直观的分析出模型是否存在较大偏差以及结果的正确性。以图像分类为例,若类别间样本数量很不平衡时,我们需要重点关注少样本类别在验证集的结果是否和训练集的出入较大,对出错类别可进一步进行模型数值分析以及可视化结果分析,进一步确认模型的行为。
3、监控训练和验证误差。首先很多情况下,我们忽略代码的规范性和算法撰写正确性验证,这点上容易产生致命的影响。在训练和验证都存在问题时,首先请确认自己的代码是否正确。其次,根据训练和验证误差进一步追踪模型的拟合状态。若训练数据集很小,此时监控误差则显得格外重要。确定了模型的拟合状态对进一步调整学习率的策略的选择或者其他有效超参数的选择则会更得心应手。
1.7.2 为什么要做学习率调整?
学习率可以说是模型训练最为重要的超参数。通常情况下,一个或者一组优秀的学习率既能加速模型的训练,又能得到一个较优甚至最优的精度。过大或者过小的学习率会直接影响到模型的收敛。我们知道,当模型训练到一定程度的时候,损失将不再减少,这时候模型的一阶梯度接近零,对应Hessian 矩阵通常是两种情况,一、正定,即所有特征值均为正,此时通常可以得到一个局部极小值,若这个局部极小值接近全局最小则模型已经能得到不错的性能了,但若差距很大,则模型性能还有待于提升,通常情况下后者在训练初最常见。二,特征值有正有负,此时模型很可能陷入了鞍点,若陷入鞍点,模型性能表现就很差。以上两种情况在训练初期以及中期,此时若仍然以固定的学习率,会使模型陷入左右来回的震荡或者鞍点,无法继续优化。所以,学习率衰减或者增大能帮助模型有效的减少震荡或者逃离鞍点。
参考链接
2 梯度下降
2.1 方向导数和梯度
2.1.1 方向导数
方向导数指的是函数z=f(x,y)z=f(x,y)在某一点PP沿某一方向的变化率,其表示形式为
∂f∂l∂f∂l
其中ll表示变换的方向。
设函数z=f(x,y)z=f(x,y)在点P(x,y)P(x,y)的某一邻域U(p)U(p)内有定义。自点PP处引射线ll,设射线ll和XX轴正向的夹角为θθ,并且假定射线ll与函数z=f(x,y)z=f(x,y)的交点为P′(x+Δx,y+Δy)P′(x+Δx,y+Δy)。则函数在P,P′P,P′的增量为f(x+Δx,y+Δy)−f(x,y)f(x+Δx,y+Δy)−f(x,y),两点之间的距离为ρ=(Δx)2+(Δy)2−−−−−−−−−−−−√ρ=(Δx)2+(Δy)2,当P′P′沿着ll趋近于PP时,如果函数增量和两点距离的比值的极限存在,则称这个极限为函数f(x,y)f(x,y)在点PP沿方向ll的方向导数,记为∂f∂l∂f∂l,即
∂f∂l=limρ→0f(x+Δx,y+Δy)−f(x,y)ρ∂f∂l=limρ→0f(x+Δx,y+Δy)−f(x,y)ρ
假设,函数z=f(x,y)z=f(x,y)在点P(x,y)P(x,y)可微,则有:
f(x+Δx,y+Δy)−f(x,y)=∂f∂x⋅Δx+∂f∂y⋅Δy+o(ρ)f(x+Δx,y+Δy)−f(x,y)=∂f∂x⋅Δx+∂f∂y⋅Δy+o(ρ)
将上式的左右两边同时除以ρρ
f(x+Δx,y+Δy)−f(x,y)ρ=∂f∂x⋅cosθ+∂f∂y⋅sinθ+o(ρ)ρf(x+Δx,y+Δy)−f(x,y)ρ=∂f∂x⋅cosθ+∂f∂y⋅sinθ+o(ρ)ρ
取极限有
∂f∂l=limρ→0f(x+Δx,y+Δy)−f(x,y)ρ=fx⋅cosθ+fy⋅sinθ∂f∂l=limρ→0f(x+Δx,y+Δy)−f(x,y)ρ=fx⋅cosθ+fy⋅sinθ
2.1.2 梯度
梯度是和方向导数相关的一个概念。
假设函数z=f(x,y)z=f(x,y)在平面区域内DD内具有一阶连续偏导数,则对每一点(x,y)∈D(x,y)∈D,都可得到一个向量,
∂f∂xi+∂f∂yj∂f∂xi+∂f∂yj
该向量就称为函数z=f(x,y)z=f(x,y)在点(x,y)(x,y)处的梯度,记为gradf(x,y)gradf(x,y),即
∇f=gradf(x,y)=∂f∂xi+∂f∂yj∇f=gradf(x,y)=∂f∂xi+∂f∂yj
那么梯度和方向导数,有什么样的关系呢。
设,向量e=cosθi+sinθje=cosθi+sinθj是与ll同向的单位向量,则有方向导数的计算公式可知,
∂f∂l=∂f∂xcosθ+∂f∂ysinθ=[∂f∂x,∂f∂y][cosθ,sinθ]T=∇f⋅e=∣∇f∣cos<∇f,e>∂f∂l=∂f∂xcosθ+∂f∂ysinθ=[∂f∂x,∂f∂y][cosθ,sinθ]T=∇f⋅e=∣∇f∣cos<∇f,e>
cos<∇f,e>cos<∇f,e>表示梯度 ∇f∇f 与 ee的夹角,当方向向量的方向ll的方向与梯度一致时,方向导数∂f∂l∂f∂l达到最大值,也就是说函数沿着梯度的方向增长最快。
函数在某点的梯度是一个向量,在该点沿着梯度方向的方向导数取得最大值,方向导数的最大值为梯度的模。
∣∇f∣=f2x+f2y−−−−−−√∣∇f∣=fx2+fy2
梯度的方向由梯度向量相对于xx轴的角度给出,
α(x,y)=arctan(fyfx)α(x,y)=arctan(fyfx)
也就是说,一个函数在某点沿着梯度的方向增长最快,而逆着梯度的方向则减小最快。
2.2 梯度下降优化算法
在复杂函数求最小值的优化问题中,通常利用上面描述的梯度的性质,逆着梯度的方向不断下降,来找到函数的极小值。
以进行一个线性回归的批量梯度下降为例,描述下梯度下降方法的过程
hθ(xi)=θ1xi+θ0hθ(xi)=θ1xi+θ0
其目标函数为:
J(θ0,θ1)=12m∑i=1m(hθ(xi)−yi)2J(θ0,θ1)=12m∑i=1m(hθ(xi)−yi)2
其中,i=1,2,⋯,mi=1,2,⋯,m为第ii个样本。这里的目标函数是所有样本误差和的均值。
则使用梯度下降进行优化时,有以下步骤
- 求目标函数的导数
ΔJ(θ0,θ1)Δθj=1m∑i=1m(hθ(x(i))−y(i))x(i)jΔJ(θ0,θ1)Δθj=1m∑i=1m(hθ(x(i))−y(i))xj(i)
i=1,2,⋯,mi=1,2,⋯,m为样本数。
- 利用上述样本更新参数
θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))x(i)jθj:=θj−α1m∑i=1m(hθ(x(i))−y(i))xj(i)
其中,αα是每次下降的步长。
梯度下降中的几个基本概念:
- 假设模型,上面线性回归中使用函数hθ(xi)=θ1xi+θ0hθ(xi)=θ1xi+θ0作为训练集的拟合函数。在深度学习中,可以将整个神经网络看着一个复杂的非线性函数,作为训练样本的拟合模型。
- 目标函数,也称为损失函数(loss function)。使用该函数的值来评估假设的模型的好坏,目标函数的值越小,假设模型拟合训练数据的程度就越好。使用梯度下降,实际就是求目标函数极小值的过程。上述线性回归中,使用模型预测值和真实数据的差值的平方作为目标函数J(θ0,θ1)=12m∑mi=1(hθ(xi)−yi)2J(θ0,θ1)=12m∑i=1m(hθ(xi)−yi)2,前面乘以1212是为了求梯度方便。
步长αα,超参数步长值的设定在梯度下降算法中是很重要的。目标函数的梯度只是指明了下降的方向,而步长则是每次迭代下降的距离多少。过小的步长,则会导致训练时间过长,收敛慢;而过大的步长则会导致训练震荡,而且有可能跳过极小值点,导致发散。
2.3 梯度下降的形式
梯度下降是机器学习的常用优化方法,根据每次使用的样本的数据可以将梯度下降分为三种形式:批量梯度下降(Batch Gradient Descent),随机梯度下降(Stochastic Gradient Descent)以及小批量梯度下降(Mini-batch Gradient Descent)。
以进行一个线性回归为例:
hθ(xi)=θ1xi+θ0hθ(xi)=θ1xi+θ0
其目标函数为:
J(θ0,θ1)=12m∑i=1m(hθ(xi)−yi)2J(θ0,θ1)=12m∑i=1m(hθ(xi)−yi)2
其中,i=1,2,⋯,mi=1,2,⋯,m为第ii个样本。这里的目标函数是所有样本误差和的均值。
则目标函数与参数(θ0,θ1)(θ0,θ1)之间关系为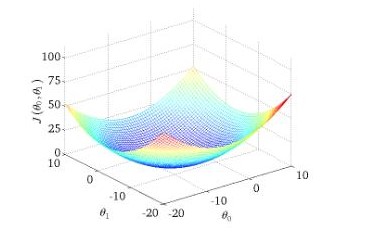
在上图中,使用梯度下降的方法,求得最低位置的(θ0,θ1)(θ0,θ1)即为所求。2.3.1 批量梯度下降
批量梯度下降是最原始的形式,它指的是每一次迭代时使用说有样本的数据进行梯度更新.
求目标函数的导数
ΔJ(θ0,θ1)Δθj=1m∑i=1m(hθ(x(i))−y(i))x(i)jΔJ(θ0,θ1)Δθj=1m∑i=1m(hθ(x(i))−y(i))xj(i)
i=1,2,⋯,mi=1,2,⋯,m为样本数。
- 利用上述样本更新参数
θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))x(i)jθj:=θj−α1m∑i=1m(hθ(x(i))−y(i))xj(i)
批量梯度下降算法的优缺点都很明显:
- 优点 每次更是时使用了全部的样本数据,能更准确地朝向极值所在的方向。
- 缺点 当样本很多时,每次都是用所有的样本,训练时每轮的计算量会很大。
从迭代次数来说,批量梯度下降迭代次数较少。对于凸误差函数,批量梯度下降法能够保证收敛到全局最小值,对于非凸函数,则收敛到一个局部最小值。
2.3.2 随机梯度下降 SGD
不同于批量梯度下降,随机梯度下降,每次只用要给样本进行梯度更新,这样训练的速度快上不少。
其目标函数为
J(i)(θ0,θ1)=12(hθ(x(i))−y(i))2J(i)(θ0,θ1)=12(hθ(x(i))−y(i))2
- 目标函数求导
ΔJ(i)(θ0,θ1)θj=(hθ(x(i))−y(i))x(i)jΔJ(i)(θ0,θ1)θj=(hθ(x(i))−y(i))xj(i)
- 梯度更新
θj:=θj−α(hθ(x(i))−y(i))x(i)jθj:=θj−α(hθ(x(i))−y(i))xj(i)
随机梯度下降每次只是用一个样本,其训练速度快。 但是在更新参数的时候,由于每次只有一个样本,并不能代表全部的训练样本,在训练的过程中SGD会一直的波动,这就使得要收敛某个最小值较为困难。不过,已经有证明缓慢减小学习率,SGD与批梯度下降法具有相同的收敛行为,对于非凸优化和凸优化,可以分别收敛到局部最小值和全局最小值。
2.3.3 小批量梯度下降,也称为随机批量梯度下降
在深度学习中,最常用的优化方法就是小批量梯度下降。 小批量下降是对批量梯度下降和随机梯度下降两种方法的中和,每次随机的使用batch_size个样本进行参数更新,也可以称为随机批量梯度下降。(batch_size是一个超参数)。
- 优点 算是对上面两种方法均衡,即有SGD训练快的优点,每次更新参数时使用多个样本,在训练的过程中较为稳定。
- 确定 batch_size是一个超参数,需要手动的指定。过大和过小的batch_size会带来一定的问题。
通常,小批量数据的大小在50到256之间,也可以根据不同的应用有所变化。在一定范围内,一般来说batch_Size越大,其确定的下降方向越准,引起训练震荡越小。但是,batch_size增大到一定程度后,其确定的下降方向并不会改变了,所以,过大的batch_size对训练精度已经帮助不大,只会增加训练的计算量。
2.4 梯度下降的难点
梯度下降的难点:
- 学习率的设置
- 极小值点,鞍点
梯度下降优化中的第一个难点就是上面提到的,学习率的设置问题。学习速率过小时收敛速度慢,而过大时导致训练震荡,而且可能会发散。
而非凸误差函数普遍出现在神经网络中,在优化这类函数时,另一个难点是梯度下降的过程中有可能陷入到局部极小值中。也有研究指出这种困难实际上并不是来自局部最小值,而更多的来自鞍点,即那些在一个维度上是递增的,而在另一个维度上是递减的。这些鞍点通常被具有相同误差的点包围,因为在任意维度上的梯度都近似为0,所以SGD很难从这些鞍点中逃开。
鞍点(Saddle point)在微分方程中,沿着某一方向是稳定的,另一条方向是不稳定的奇点,叫做鞍点。对于拥有两个以上变量的曲线,它的曲面在鞍点好像一个马鞍,在某些方向往上曲,在其他方向往下曲。由于鞍点周围的梯度都近似为0,梯度下降如果到达了鞍点就很难逃出来。下图是z=x2−y2z=x2−y2图形,在x轴方向向上曲,在y轴方向向下曲,像马鞍,鞍点为(0,0)(0,0)
另外,在梯度平坦的维度下降的非常慢,而在梯度较大的维度则有容易发生抖动。
2.5 梯度下降的算法的进化
理想的梯度下降算法要满足两点:收敛速度要快;而且能全局收敛。所以就有各种梯度算法的变种。
2.5.1 动量梯度下降
基于动量的梯度下降是根据指数加权平均来的,首先要了解下指数加权平均。
2.5.1.1 指数加权平均
指数加权平均(exponentially weighted averges),也称为指数加权移动平均,是常用的一种序列数据的处理方法。设在tt时刻数据的观测值是θtθt,在tt时刻的移动平均值为vtvt,则有
vt=βvt−1+(1−β)θtvt=βvt−1+(1−β)θt
其中,βvt−1βvt−1是上一时刻的移动平均值,也看着一个历史的积累量。通常设v0=0v0=0,ββ是一个参数,其值在(0,1)(0,1)之间。动平均值实际是按比例合并历史量与当前观测量,将上述递推公司展开
v0v1v2⋮vt=0=βv0+(1−β)θ1=βv1+(1−β)θ2=β(βv0+θ1)+(1−β)θ2=βvt−1+(1−β)θt=∑i=1tβt−i(1−β)θtv0=0v1=βv0+(1−β)θ1v2=βv1+(1−β)θ2=β(βv0+θ1)+(1−β)θ2⋮vt=βvt−1+(1−β)θt=∑i=1tβt−i(1−β)θt
展开后可以发现,在计算某时刻的vtvt时,其各个时刻观测值θtθt的权值是呈指数衰减的,离当前时刻tt越近的θtθt,其权值越大,也就是说距离当前时刻越近的观测值对求得移动平均值的影响越大,这样得到的平均值的会比较平稳。由于权重指数衰减,所以移动平均数只是计算比较相近时刻数据的加权平均数,一般认为这个时刻的范围为11−β11−β,例如β=0.9β=0.9,可以认为是使用距离当前时刻之前10时刻内的θtθt的观测值,再往前由于权重值国小,影响较小。
2.5.1.2 指数加权平均例子
下面是伦敦一年中每天的温度,使用指数加权平均的方法,来表示其温度的变化趋势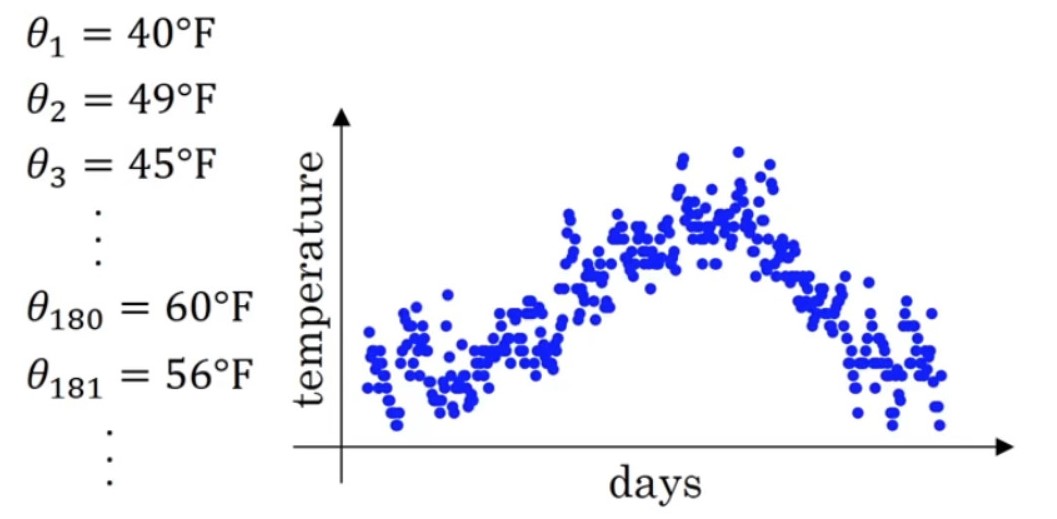
计算其各个时刻的移动品均值,设β=0.9β=0.9
v0v1v2⋮vt=0=0.9v0+0.1θ1=0.9v1+0.1θ2=0.9vt−1+0.1θtv0=0v1=0.9v0+0.1θ1v2=0.9v1+0.1θ2⋮vt=0.9vt−1+0.1θt
将移动平均值即每日温度的指数加权平均值的曲线图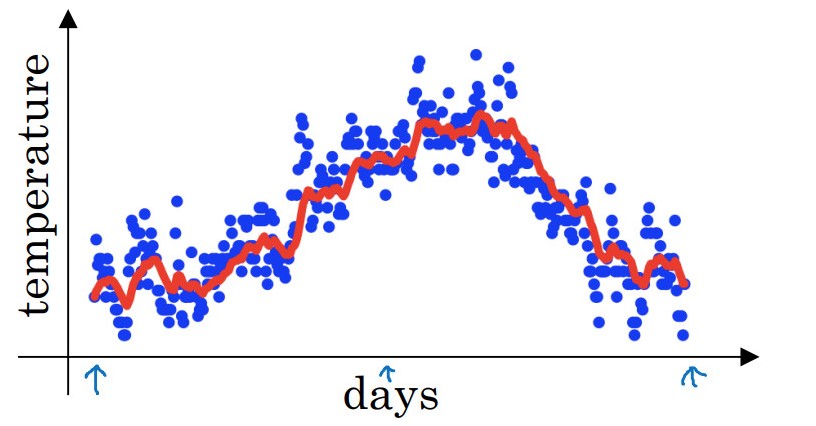
上图的 β=0.9β=0.9,也就是近10天的加权平均值。设β=0.98β=0.98,也就是近50天的加权均值,可以得到如下曲线(绿色)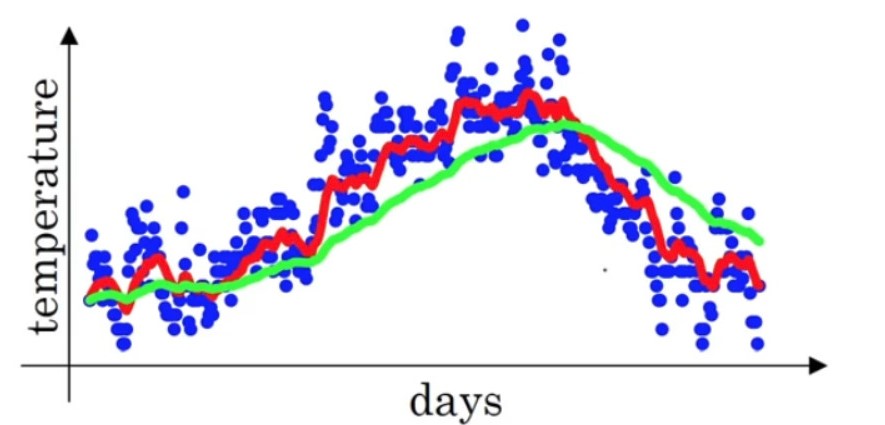
相比于红色曲线,绿色曲线更为平坦,因为使用50天的温度,所以这个曲线,波动更小,更加平坦,缺点是曲线进一步右移,因为现在平均的温度值更多,要平均更多的值,指数加权平均公式在温度变化时,适应地更缓慢一些,所以会出现一定延迟。而且β=0.98β=0.98给历史积累量的权值过多,而给当前量权值仅为0.02过少。
那如果平均过少的天数呢,比如β=0.5β=0.5只使用2天内的温度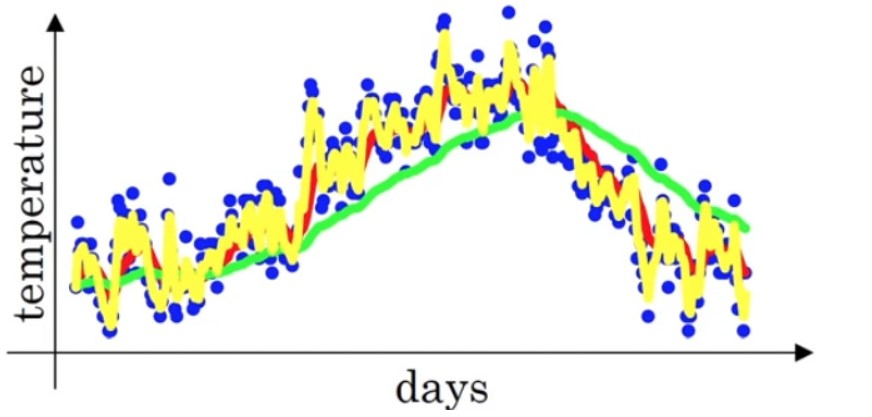
可以看到黄色曲线波动较大,有可能出现异常值,但是这个曲线能够更快适应温度变化。
参数ββ的选择较为重要,不能过大或者国小。在本例中,β=0.9β=0.9取得的红色曲线,显然更能表示温度变化的趋势。
2.5.1.3 动量梯度下降
动量梯度下降算法是Boris Polyak在1964年提出的,其基于这样一个物理事实:将一个小球从山顶滚下,其初始速率很慢,但在加速度作用下速率很快增加,并最终由于阻力的存在达到一个稳定速率。
mθ←γ⋅m+η⋅∇J(θ)←θ−mm←γ⋅m+η⋅∇J(θ)θ←θ−m
可以看到,在更新权值时,不仅仅使用当前位置的梯度,还加入了一个累计项:动量,多了也给超参数γγ。
动量梯度下降,实际上是引入了指数加权平均,在更新参数时不仅仅的只考虑当前梯度的值,还要考虑前几次梯度的值。
vtθ=βvt−1+(1−β)∇J(θ)t=θ−αvtvt=βvt−1+(1−β)∇J(θ)tθ=θ−αvt
将学习速率αα整合到第一个式子中,更简洁一些
vtθ=γvt−1+η∇J(θ)t=θ−vtvt=γvt−1+η∇J(θ)tθ=θ−vt
在进行参数更新时,使用当前的vtvt移动平均值来代替当前的梯度,进行参数更新。所谓的动量,也就是近几次的梯度加权移动平均。例如,通常有β=0.9β=0.9,也就是当前时刻最近的10次梯度做加权平均,然后用次平均值更新参数。
如下图,红点代表最小值的位置
原始的梯度下降算法,会在纵轴上不断的摆动,这种波动就就减慢了梯度下降的速度。理想情况是,在纵轴上希望学习的慢一点,而在横轴上则要学习的快一点,尽快的达到最小值。 要解决这个问题有两种思路:
- 纵轴方向和横轴方向设置不同的学习率,这是自适应学习速率算法的方法。后面会说到,这里先不提。
- 带动量的梯度下降。
如上图,在纵轴方向其每次的梯度摇摆不定,引入动量后,每次使用一段时间的梯度的平均值,这样不同方向的梯度就会相互抵消,从而减缓纵轴方向的波动。而在,横轴方向,由于每次梯度的方向都指向同一个位置,引入动量后,其平均后的均值仍然指向同一个方向,并不会影响其下降的速度。
动量梯度下降,每一次梯度下降都会累积之前的速度的作用,如果这次的梯度方向与之前相同,则会因为之前的速度继续加速;如果这次的方向与之前相反,则会由于之前存在速度的作用不会产生一个急转弯,而是尽量把路线向一条直线拉过去,这样就减缓的波动。
2.5.2 Nesterov Accelerated Gradient,NAG
球从山上滚下的时候,盲目地沿着斜率方向,往往并不能令人满意。我们希望有一个智能的球,这个球能够知道它将要去哪,以至于在重新遇到斜率上升时能够知道减速。
NAG算法是Yurii Nesterov在1983年提出的对冲量梯度下降算法的改进版本,其速度更快。其变化之处在于计算“超前梯度”更新冲量项。
在动量梯度下降中,使用动量项γvt−1γvt−1来更新参数θθ,通过计算θ−γvt−1θ−γvt−1能够大体预测更新后参数所在的位置,也就是参数大致将更新为多少。通过计算关于参数未来的近似位置的梯度,而不是关于当前的参数的梯度位置
vtθ=γvt−1+η∇J(θ−γvt−1)=θ−vtvt=γvt−1+η∇J(θ−γvt−1)θ=θ−vt
如下图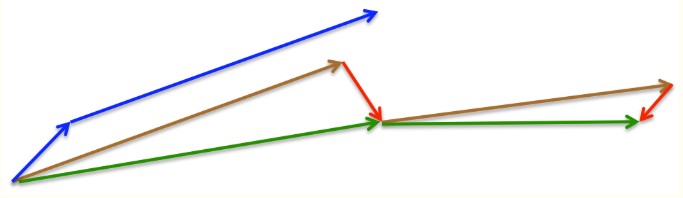
动量梯度下降,首先计算当前的梯度项,上图的蓝色小向量;然后加上累积的动量项,得到大蓝色向量,在改方向上前进一步。
NAG则首先在之前累积的动量项(棕色向量)前进一步,计算梯度值,然后做一个修正(绿色的向量)。这个具有预见性的更新防止我们前进得太快,同时增强了算法的响应能力。
直观想象下这个过程,就像骑一辆自行车向下冲。一般的动量下降,就像骑到某一个地方,然后根据当前的坡度,决定往那个方向拐。而NAG则是首先判断下前方的坡度,然后根据前方的坡度决定往那个方向拐。也就是预判下一个位置的坡度,对当前下降的方向进行修正,避免走冤枉路。
2.5.3 AdaGrad
在基本的梯度优化算法中,有个常见问题是,要优化的变量对于目标函数的依赖是不相同的。有些变量,已经优化到极小值附近,但是有些变量仍然离极小值很远,位于梯度较大的地方。这时候如果对所有的变量都使用同一个全局的优学习速率就有可能出现问题,学习率太小,则梯度很大的变量就会收敛的很慢;如果梯度很大,已经优化的差不多的变量可能会不稳定。
针对这个问题,Jhon Duchi提出了AdaGrad(Adaptive Gradient),自适应学习速率。AdaGrad的基本思想是对每个变量使用不同的学习率。在最初,学习速率较大,用于快速下降。随着优化过程的进行,对于已经下降很多的变量,则减小学习率;对于没有怎么下降的变量,则仍保持大的学习率。
AdaGrad对每个变量更新时,利用该变量历史积累的梯度来修正其学习速率。这样,已经下降的很多的变量则会有小的学习率,而下降较少的变量则仍然保持较大的学习率。基于这个更新规则,其针对变量θiθi的更新
θ(t+1,i)=θ(t,i)−η∑tτ=1∇J(θi)τ+ϵ−−−−−−−−−−−−−−√⋅∇J(θi)t+1θ(t+1,i)=θ(t,i)−η∑τ=1t∇J(θi)τ+ϵ⋅∇J(θi)t+1
其中,∇J(θi)t∇J(θi)t表示t时刻变量θiθi的梯度。∑tτ=1∇J(θi)τ∑τ=1t∇J(θi)τ就表示变量θiθi历史累积的梯度值 ,用来修正学习率。加上很小的值ττ是为了防止0的出现。
AdaGrad虽然能够动态调整变量的学习率,但是其有两个问题:
- 仍然需要手动的设置一个初始的全局学习率
- 使用变量的历史累积梯度来调整学习率,这就导致其学习率是不断衰减的,训练后期学习速率很小,导致训练过早停止。
后面的几种自适应算法都是对AdaGrad存在的上述问题进行修改.
2.5.4 RMSprop
RMSprop是Hinton在他的课程上讲到的,其算是对Adagrad算法的改进,主要是解决学习速率过快衰减的问题。其思路引入了动量(指数加权移动平均数)的方法,引入了超参数γγ,在累积梯度的平方项近似衰减:
s(t,i)θ(t,i)=γs(t−1,i)+(1−γ)∇J(θi)t⊙∇J(θi)t=θ(t−1,i)−ηs(t,i)+ϵ−−−−−−−√⊙∇J(θi)ts(t,i)=γs(t−1,i)+(1−γ)∇J(θi)t⊙∇J(θi)tθ(t,i)=θ(t−1,i)−ηs(t,i)+ϵ⊙∇J(θi)t
其中,ii表示第ii个变量,tt表示tt时刻更新,γγ是超参数通常取γ=0.9γ=0.9。s(t,i)s(t,i)表示梯度平方的指数加权移动平均数,用来代替AdaGrad中不断累加的历史梯度,有助于避免学习速率衰减过快的问题。同时Hinton也建议将全局的学习率ηη设置为0.001。
2.5.5 AdaDelta
AdaDelta对AdaGrad进行两方面的改进:
- 学习率衰减过快
- 全局学习率超参数问题
针对学习率衰减过快的问题,其思路和RMSprop一样,不在累积所有的历史梯度,而是引入指数加权平均数,只计算一定时间段的梯度。
s(t,i)θ(t,i)=γs(t−1,i)+(1−γ)∇J(θi)t⊙∇J(θi)t=θ(t−1,i)−ηs(t,i)+ϵ−−−−−−−√⊙∇J(θi)ts(t,i)=γs(t−1,i)+(1−γ)∇J(θi)t⊙∇J(θi)tθ(t,i)=θ(t−1,i)−ηs(t,i)+ϵ⊙∇J(θi)t
为了解决学习率超参数的问题,AdaDelta维护了一个额外的状态变量ΔθtΔθt,根据上面的公式有
Δθt=−ηs(t,i)+ϵ−−−−−−−√⊙∇J(θi)tΔθt=−ηs(t,i)+ϵ⊙∇J(θi)t
上述使用的是梯度平方的指数加权移动平均数,在AdaDelta中作者又定义了:每次参数的更新值ΔθΔθ的平方的指数加权移动平均数
E(Δθ2)t=γE(Δθ2)t−1+(1−γ)Δθ2tE(Δθ2)t=γE(Δθ2)t−1+(1−γ)Δθt2
因此每次更新时,更新值的均方根(Root Mean Squard,RMS)
RMS(Δθ)t=E(Δθ2)t+ϵ−−−−−−−−−−√RMS(Δθ)t=E(Δθ2)t+ϵ
使用RMS(Δθ)t−1RMS(Δθ)t−1来近似更新tt时刻的学习速率ηη,这样可以得到其更新的规则为
θ(t,i)=θ(t−1,i)−RMS(Δθ)t−1s(t,i)+ϵ−−−−−−−√⊙∇J(θi)tθ(t,i)=θ(t−1,i)−RMS(Δθ)t−1s(t,i)+ϵ⊙∇J(θi)t
设初始的RMS(Δθ)0=0RMS(Δθ)0=0,这样就不用设置默认的学习速率了。 也就是,AdaDelta和RMSprop唯一的区别,就是使用RMS(Δθ)t−1RMS(Δθ)t−1来代替超参数学习速率。 至于为什么可以代替,使用牛顿迭代的思想,这里不再说明,有兴趣可以参看原始论文ADADELTA: An Adaptive Learning Rate Method 。
2.5.6 Adam
Adaptive moment estimation,Adam 是Kingma等在2015年提出的一种新的优化算法,其结合了Momentum和RMSprop算法的思想。相比Momentum算法,其学习速率是自适应的,而相比RMSprop,其增加了冲量项。所以,Adam是两者的结合体。
Adam不只使用梯度平方的指数加权移动平均数vtvt,还使用了梯度的指数加权移动平均数mtmt,类似动量。
mtvt=β1mt−1+(1−β1)gt=β2vt−1+(1−β2)g2tmt=β1mt−1+(1−β1)gtvt=β2vt−1+(1−β2)gt2
可以看到前两项和Momentum和RMSprop是非常一致的, 由于和的初始值一般设置为0,在训练初期其可能较小,需要对其进行放大
m^tv^t=mt1−βt1=vt1−βt2m^t=mt1−β1tv^t=vt1−β2t
这样就得到了更新的规则
θt+1=θt−ηv^t−−√+ϵm^tθt+1=θt−ηv^t+ϵm^t
作者建议β1β1设置为0.9,β2β2设置为0.999,取ϵ=10−8ϵ=10−8。
2.6 Summary
下图给出各个梯度下降算法的可视化下降过程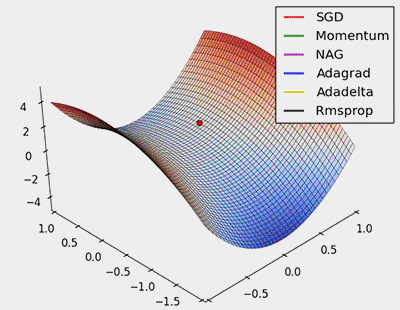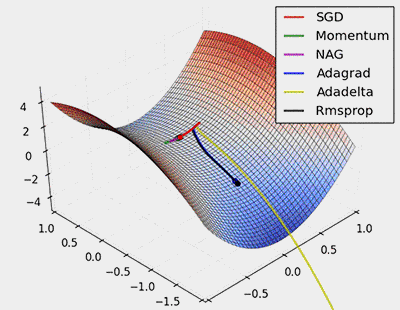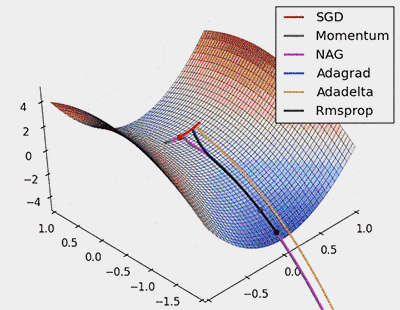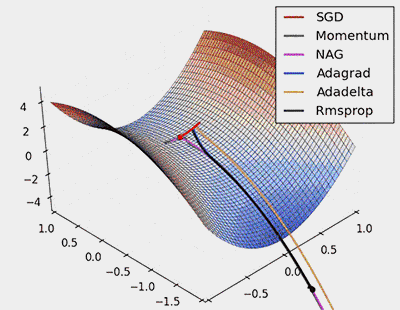
本文综述了一些常见的梯度下降方法,主要是自适应梯度下降。 由于超参数学习速率的难以设定,自适应梯度下降有很好的实用价值。除了使用自适应梯度下降算法外,也可以手动的设定学习速率的自适应过程,例如学习速率的多项式衰减等。
参考文献
3 语义信息、高层特征和底层特征
3.1 图像的语义信息
图像的语义分为视觉层、对象层和概念层,视觉层即通常所理解的底层,即颜色、纹理和形状等等,这些特征都被称为底层特征语义;对象层即中间层,通常包含了属性特征等,就是某一对象在某一时刻的状态;概念层是高层,是图像表达出的最接近人类理解的东西。通俗点说,比如一张图上有沙子,蓝天,海水等,视觉层是一块块的区分,对象层是沙子、蓝天和海水这些,概念层就是海滩,这是这张图表现出的语义。
3.2 图像的底层、高层特征
3.2.1 图像的低层特征
图像底层特征指的是:轮廓、边缘、颜色、纹理和形状特征。<br /> 边缘和轮廓能反映图像内容;如果能对边缘和关键点进行可靠提取的话,很多视觉问题就基本上得到了解决。图像的低层的特征语义信息比较少,但是目标位置准确;
3.2.2 图像的高层特征
图像的高层语义特征值得是我们所能看的东西,比如对一张人脸提取低层特征我们可以提取到连的轮廓、鼻子、眼睛之类的,那么高层的特征就显示为一张人脸。高层的特征语义信息比较丰富,但是目标位置比较粗略。<br /> 愈深层特征包含的高层语义性愈强、分辨能力也愈强。我们把图像的视觉特征称为视觉空间 (visual space),把种类的语义信息称为语义空间 (semantic space)<br />[参考链接](https://blog.csdn.net/qq_30121457/article/details/108918519)
4 特征类型:工程特征和基于学习的特征
4.1 分类
根据特征类型,分为:工程特征和基于学习的特征。
4.1.1对于工程特征,分为基于纹理的局部特征、基于几何的全局特征和混合特征。
(1)基于纹理的特征主要有SIFT[49]、HOG[14]、LBP[52]直方图、Gabor小波系数[39]等。
(2)基于几何的特征主要是基于鼻子、眼睛和嘴周围的地标点。
(3)混合特征提取:将两个或两个以上的工程特征结合起来,即混合特征提取,可以进一步丰富表示形式。
4.1.2对于学习到的特征,Fasel[22]发现一个浅CNN是稳健的面对姿势和规模。
4.2 后续
Tang[57]和Kahou et al.[29]利用深度cnn进行特征提取,分别赢得了FER2013和Emotiw2013的挑战。Liu等人提出了一种基于CNN结构的面部动作单元(Facial Action Units)用于表情识别。在特征提取之后,下一步是将特征输入到一个有监督的分类器中,如支持向量机(Support Vector Machines, svm)、softmax层和逻辑回归,以分配表达式类别。为了避免在小的面部表情数据集上过拟合,最近的许多研究[45],[2],[56],[33],[72],[20]利用人脸识别数据集对网络进行预训练,然后对目标表情数据集进行微调。Levi和Hassner[33]利用CASIA-WebFace[63]人脸识别数据集来预训练四个不同的VGGNet[53]和googlet[55]。
4.3 参考文献
[2] Samuel Albanie, Arsha Nagrani, Andrea Vedaldi, and Andrew Zisserman. Emotion recognition in speech using cross-modal transfer in the wild. arXiv preprint arXiv:1808.05561, 2018. 2
[14] N. Dalal and B. Triggs. Histograms of oriented gradients for human detection. In CVPR, 2005. 2
[20] H. Ding, S. K. Zhou, and R. Chellappa. Facenet2expnet: Regularizing a deep face recognition net for expression recognition. In 2017 12th IEEE International Conference on Automatic Face Gesture Recognition (FG 2017), pages 118–126, May 2017. 2
[22] B. Fasel. Robust face analysis using convolutional neural networks. In ICPR, pages 40–43, 2002. 2
[29] Samira Ebrahimi Kahou, Christopher Pal, Xavier Bouthillier, Pierre Froumenty, Roland Memisevic, Pascal Vincent, Aaron Courville, Yoshua Bengio, and Raul Chandias Ferrari. Combining modality specifific deep neural networks for emotion recognition in video. In International Conference on Multimodal Interaction, pages 543–550, 2013. 1, 2
[33] Gil Levi and Tal Hassner. Emotion recognition in the wild via convolutional neural networks and mapped binary patterns. In Proceedings of the 2015 ACM on international conference on multimodal interaction, pages 503–510. ACM, 2015. 2
[39] Chengjun Liu and H. Wechsler. Gabor feature based classifification using the enhanced fifisher linear discriminant model for face recognition. IEEE Transactions on Image Processing, 11(4):467–476, April 2002. 2
[45] Debin Meng, Xiaojiang Peng, Kai Wang, and Yu Qiao. frame attention networks for facial expression recognition in videos. arXiv preprint arXiv:1907.00193, 2019. 2
[49] Pauline C. Ng and Steven Henikoff. Sift: predicting amino acid changes that affect protein function. Nucleic Acids Research, 31(13):3812–3814, 2003. 2
[52] Caifeng Shan, Shaogang Gong, and Peter W. McOwan. Facial expression recognition based on local binary patterns: A comprehensive study. Image and Vision Computing, 27(6):803 – 816, 2009. 2
[53] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014. 2
[55] Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1–9, 2015. 2
[56] Lianzhi Tan, Kaipeng Zhang, Kai Wang, Xiaoxing Zeng, Xiaojiang Peng, and Yu Qiao. Group emotion recognition with individual facial emotion cnns and global image based cnns. In Proceedings of the 19th
ACM International Conference on Multimodal Interaction, pages 549–552. ACM, 2017. 2
[57] Yichuan Tang. Deep learning using linear support vector machines. Computer Science, 2013. 1, 2
[63] Dong Yi, Zhen Lei, Shengcai Liao, and Stan Z Li. Learning face representation from scratch. arXiv preprint arXiv:1411.7923, 2014. 2
[72] Xiangyun Zhao, Xiaodan Liang, Luoqi Liu, Teng Li, Yugang Han, Nuno Vasconcelos, and Shuicheng Yan. Peak-piloted deep network for facial expression recognition. In European conference on computer vision, pages 425–442. Springer, 2016. 2
5 前向传播
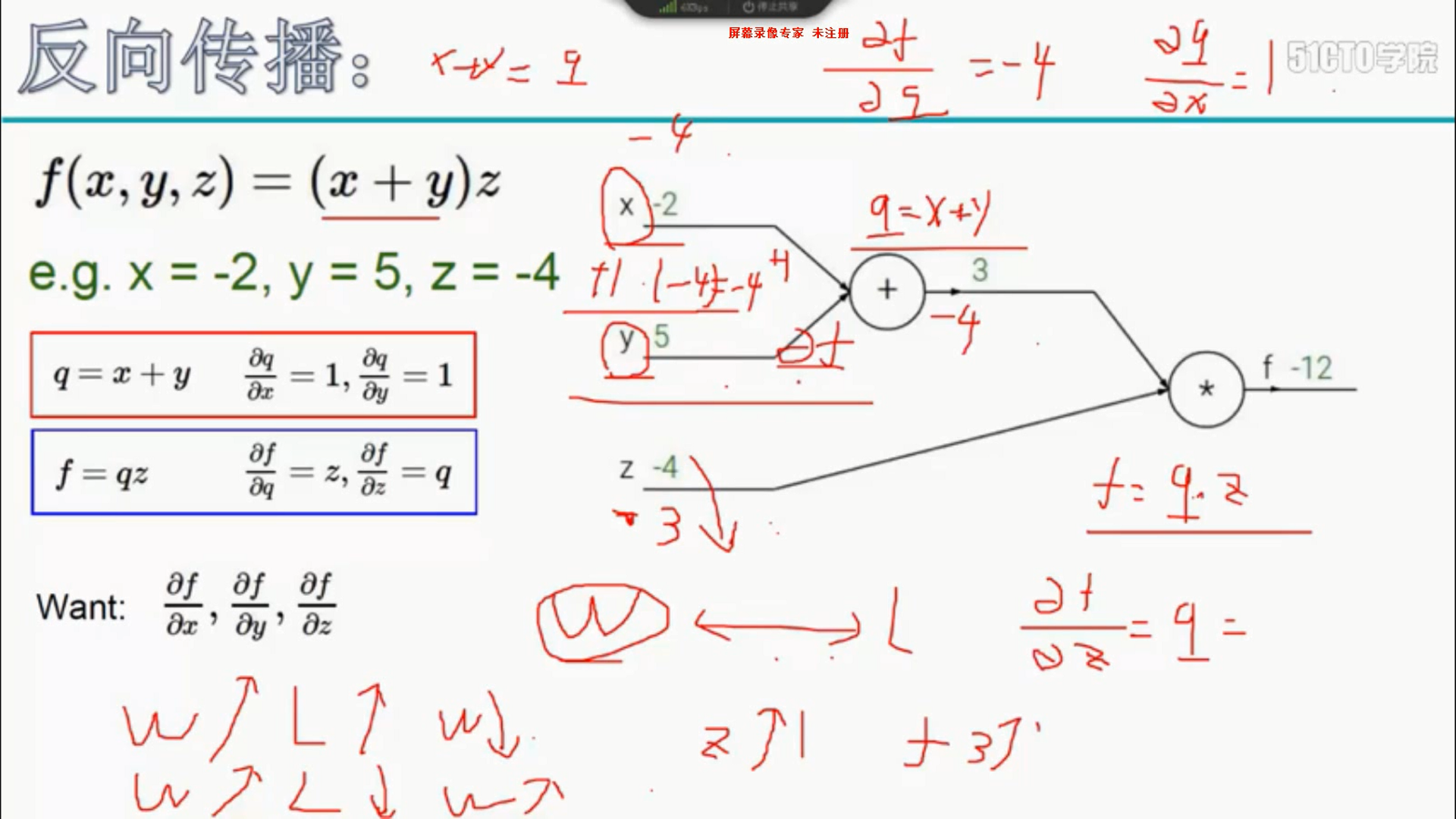
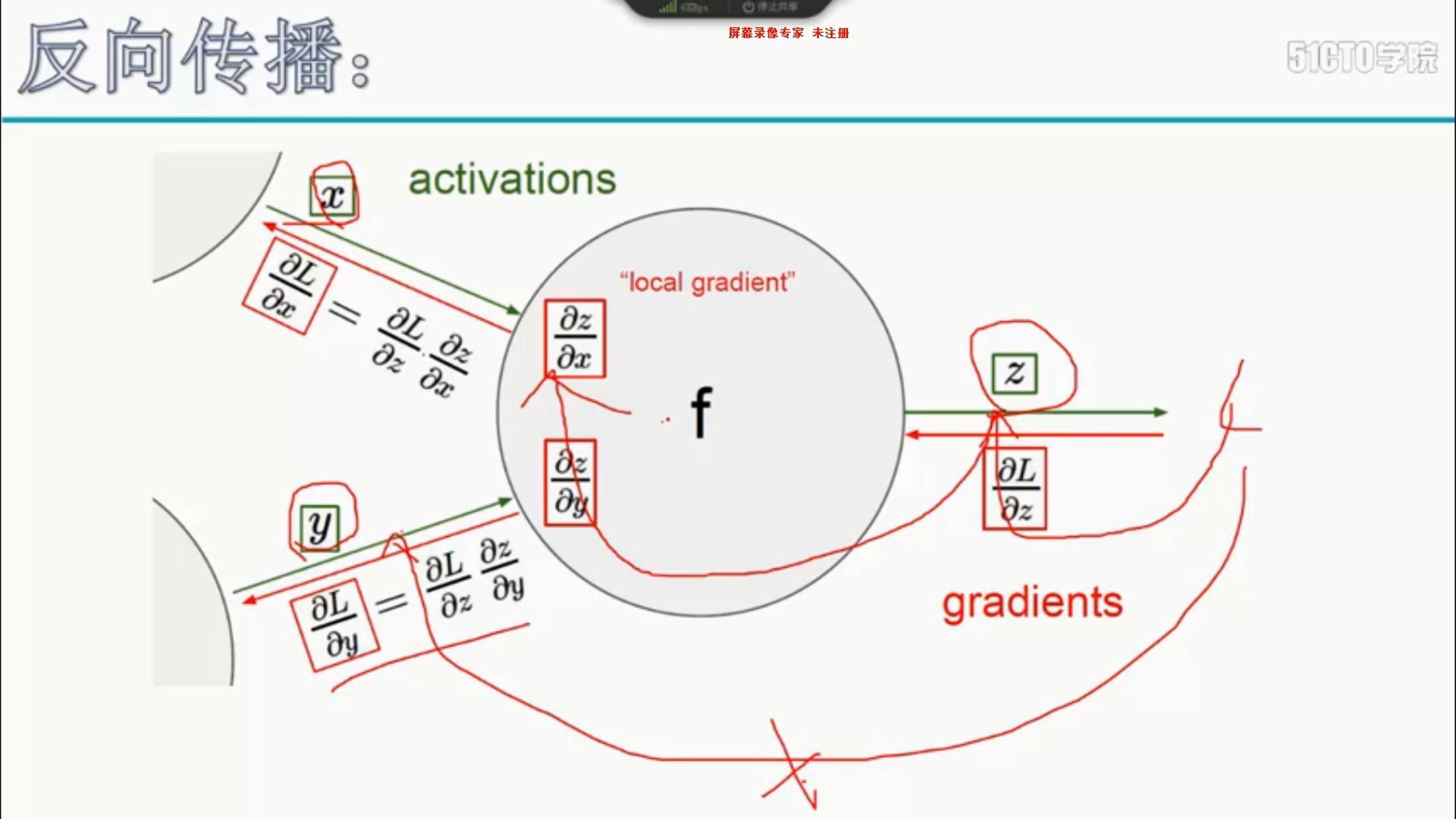
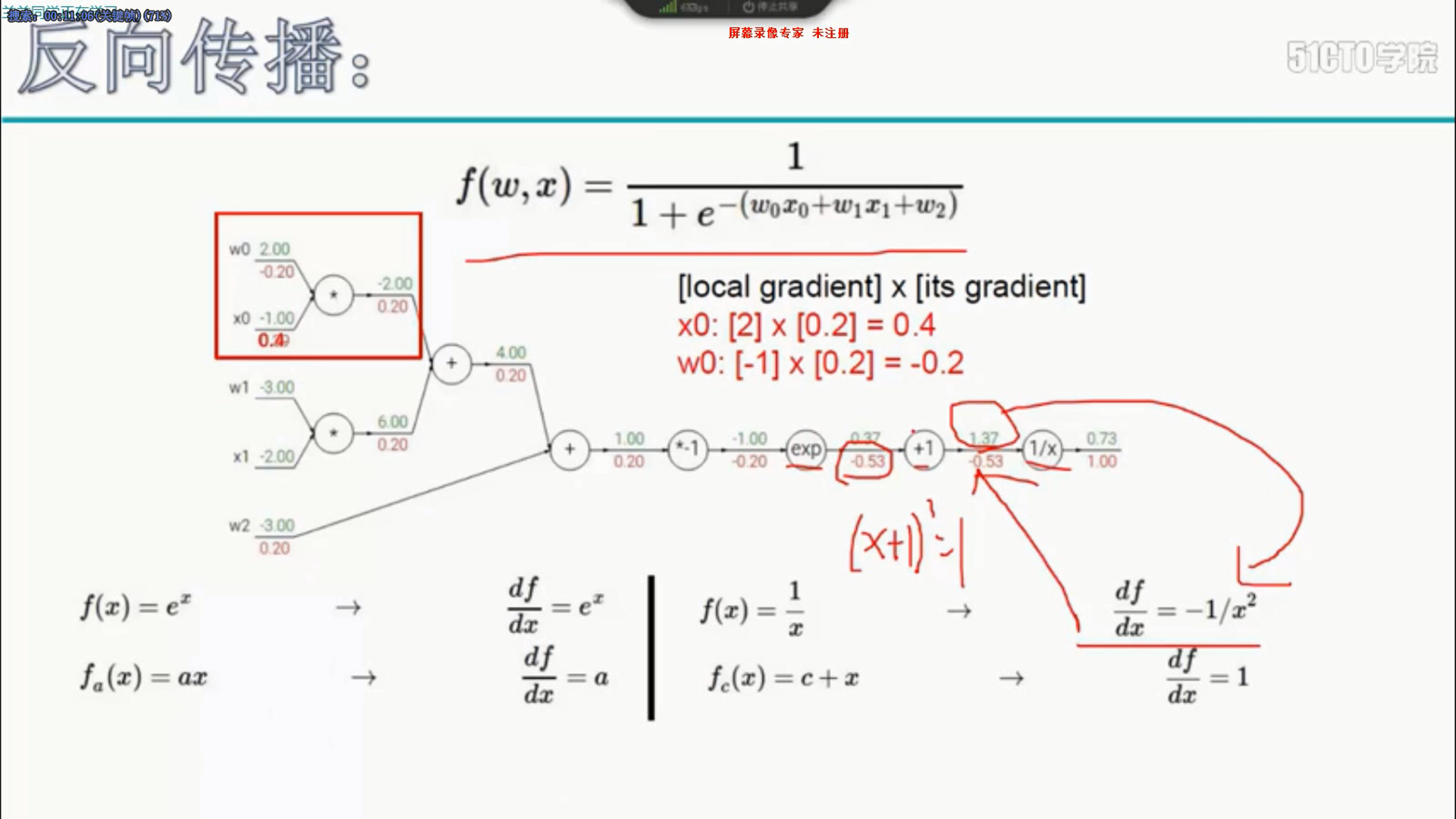
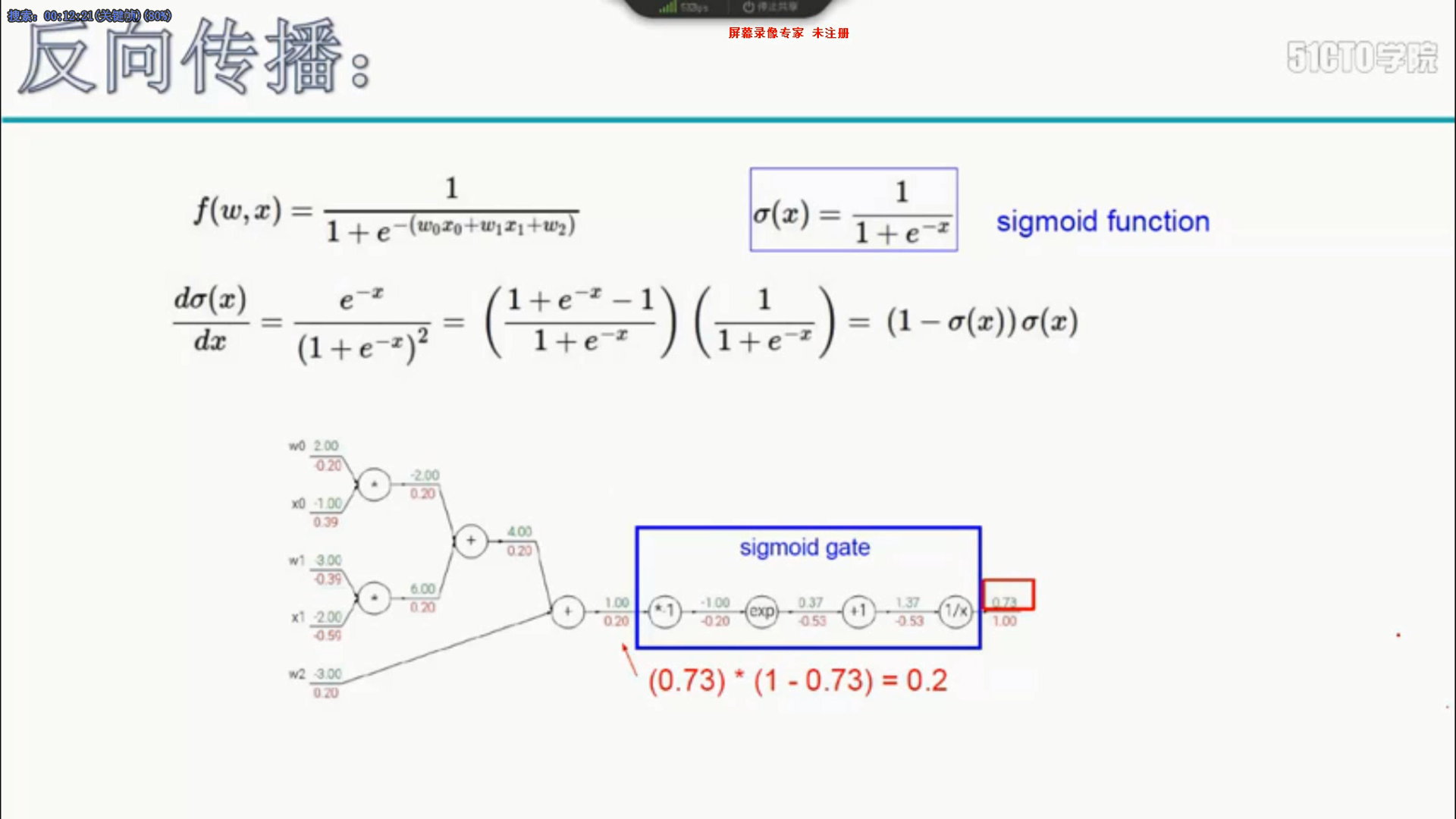
6 反向传播
7 学习率
学习率 (Learning rate) 作为监督学习以及深度学习中重要的超参,其决定着目标函数能否**收敛到局部最小值**以及何时**收敛到最小值**。
8 批次(Batch)
就是只使用训练集中的一小部分样本对模型权重进行一次反向传播的参数更新,这一小部分样本被称作批次(Batch)。例如:对一些数据进行随机排序之后,样本量为1万,如果定义Batch Size = 200,那么1万个随机排序后的数据被以200为基本规格的Batch切割成了50份,这就是50个Batch。
9 Epoch
在做数据优化时,读入第一个Batch,在这个Batch上计算梯度方向,因为Batch是随机的,所以这个方向可能也是随机的。接着参数按照这个方向做一定的更新迭代,再计算下一个Batch。当50个Batch全部做完之后,所有的样本都被遍历了一遍,这叫一个Epoch循环。Batch和Epoch的详细图解如下图所示。在做模型优化时,需要多少个Epoch循环,Batch Size设定为多少,是不容易确定的选择,常常要经过很多尝试,才可能找到一个比较让人满意的组合。
10 批量归一化和动态归一化
10.1 批量归一化(Batch Normalization)
批量归一化(Batch Normalization)的核心就是让像素取值变为均值为0,方差为1。Batch Normalization的核心思想如下图所示:
10.2 动态归一化
11 数据增强或数据增广(Data Augmentation)
Data Augmentation:是通过对数据施加各种变换(放大、缩小、旋转、横纵轴的比例变换了被拉直了(类似于把正方形拉成平行四边形)垂直向下平移、垂直向上平移、水平向左平移、水平向右平移、左右翻转等等)来达到增加样本量的目的。
经过变化后,表达图像的矩阵是不一样的。数据增强最根本的原因是矩阵对图像的表达是不充分的。
12 端对端学习
端到端的学习方法: In end-to-end reinforcement learning, the end-to-end process, in other words, the entire process from sensors to motors in a robot or agent involves a single, layered or recurrent neural network without modularization. 这是wiki对端到端学习的定义,总结起来就是不经过复杂的中间建模过程,从输入端到输出端会得到一个预测的结果,这个预测的结果与标记的真实数据之间会进行计算,得到误差结果。然后我们采用比如梯度下降的方法使得误差结果减少,模型最终达到收敛,输出最终的结果,则就是端到端的学习过程。<br /> 而与传统的机器学习的区别在与:传统的机器学习过程往往由不同的模块和不同的功能组成,比如卡尔曼滤波运用在轨迹数据的标记和运动物标的识别。这整个过程需要进行数据标注,图像数据的转换,卡尔曼滤波方法的运用等一系列的过程,而每个过程又是相互独立的,每一步都需要我们对数据进行单独的标注等工作。其坏处就是会影响结果的准确性。因此,端到端的学习我们只需要进行数据数据的一次性标注,然后送到CNN,RNN 等网络中去,得到最终结果。因此,端到端的学习可以大量的减少人为标注的工作量,同时可以使得预测的结果更能符合预期的要求。<br />[参考链接](https://blog.csdn.net/rechardchen123/article/details/86447621)
13 传统机器学习、深度学习和目前主流的开源算法框架
13.1 传统机器学习
传统机器学习从一些观测(训练)样本出发,试图发现不能通过原理分析获得的规律,实现对未来数据行为或趋势的准确预测。<br />相关算法包括:
- 逻辑回归
- 隐马尔科夫方法
- 支持向量机方法
- K 近邻方法
- 三层人工神经网络方法
- Adaboost算法
- 贝叶斯方法
- 决策树方法 等
传统机器学习平衡了学习结果的有效性与学习模型的可解释性,为解决有限样本的学习问题提供了一种框架,主要用于有限样本情况下的模式分类、回归分析、概率密度估计等。
传统机器学习方法共同的重要理论基础之一是统计学,在自然语言处理、语音识别、图像识别、信息检索和生物信息等许多计算机领域获得了广泛应用。
13.2 深度学习
深度学习是建立深层结构模型的学习方法。<br /> 典型的深度学习算法包括:
- 深度置信网络 DBN,Deep Belief Nets
- 卷积神经网络 CNN,Convolutional Neural Network
- 受限玻尔兹曼机 RBM,Restricted Boltzmann Machine
循环神经网络 RNN,recurrent neural network
深度学习又称为深度神经网络(指层数超过3 层的神经网络)。
深度学习作为机器学习研究中的一个新兴领域,由Hinton 等人于2006 年提出。
深度学习源于多层神经网络,其实质是给出了一种将特征表示和学习合二为一的方式。
深度学习的特点是放弃了可解释性,单纯追求学习的有效性。经过多年的摸索尝试和研究,已经产生了诸多深度神经网络的模型,其中卷积神经网络、循环神经网络是两类典型的模型。卷积神经网络常被应用于空间性分布数据;循环神经网络在神经网络中引入了记忆和反馈,常被应用于时间性分布数据。深度学习框架是进行深度学习的基础底层框架,一般包含主流的神经网络算法模型,提供稳定的深度学习API,支持训练模型在服务器和GPU、TPU 间的分布式学习,部分框架还具备在包括移动设备、云平台在内的多种平台上运行的移植能力,从而为深度学习算法带来前所未有的运行速度和实用性。13.3 目前主流的开源算法框架有
TensorFlow、Caffe/Caffe2、CNTK、MXNet、Paddle-paddle、Torch/PyTorch、Theano 等。
14 特征融合的方法
(1)concat:系列特征融合,直接将两个特征进行连接。两个输入特征x和y的维数若为p和q,输出特征z的维数为p+q;
(2)add:并行策略[36],将这两个特征向量组合成复向量,对于输入特征x和y,z = x + iy,其中i是虚数单位。15 聚类
15.1 聚类的定义
聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
15.2 聚类和分类的区别
聚类(Clustering):是指把相似的数据划分到一起,具体划分的时候并不关心这一类的标签,目标就是把相似的数据聚合到一起,聚类是一种无监督学习(Unsupervised Learning)方法。
- 分类(Classification):是把不同的数据划分开,其过程是通过训练数据集获得一个分类器,再通过分类器去预测未知数据,分类是一种监督学习(Supervised Learning)方法。
15.3 聚类的一般过程
- 数据准备:特征标准化和降维
- 特征选择:从最初的特征中选择最有效的特征,并将其存储在向量中
- 特征提取:通过对选择的特征进行转换形成新的突出特征
- 聚类:基于某种距离函数进行相似度度量,获取簇
- 聚类结果评估:分析聚类结果,如距离误差和(SSE)等
15.4 数据对象间的相似度度量
对于数值型数据,可以使用下表中的相似度度量方法。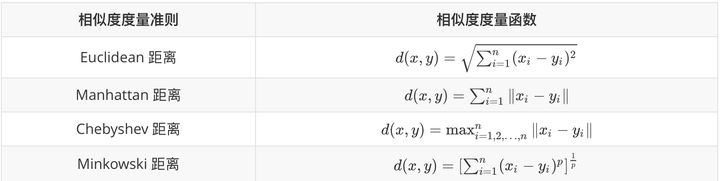
Minkowski距离就是范数(
),而 Manhattan 距离、Euclidean距离、Chebyshev距离分别对应
时的情形。
15.5 cluster之间的相似度度量
除了需要衡量对象之间的距离之外,有些聚类算法(如层次聚类)还需要衡量cluster之间的距离 ,假设和
为两个 cluster,则前四种方法定义的
和
之间的距离如下表所示。

- Single-link定义两个cluster之间的距离为两个cluster之间距离最近的两个点之间的距离,这种方法会在聚类的过程中产生链式效应,即有可能会出现非常大的cluster
- Complete-link定义的是两个cluster之间的距离为两个
`cluster之间距离最远的两个点之间的距离,这种方法可以避免链式效应,对异常样本点(不符合数据集的整体分布的噪声点)却非常敏感,容易产生不合理的聚类 - UPGMA正好是Single-link和Complete-link方法的折中,他定义两个cluster之间的距离为两个cluster之间所有点距离的平均值
- 最后一种WPGMA方法计算的是两个 cluster 之间两个对象之间的距离的加权平均值,加权的目的是为了使两个 cluster 对距离的计算的影响在同一层次上,而不受 cluster 大小的影响,具体公式和采用的权重方案有关。
15.6 数据聚类方法
数据聚类方法主要可以分为划分式聚类方法(Partition-based Methods)、基于密度的聚类方法(Density-based methods)、层次化聚类方法(Hierarchical Methods)等。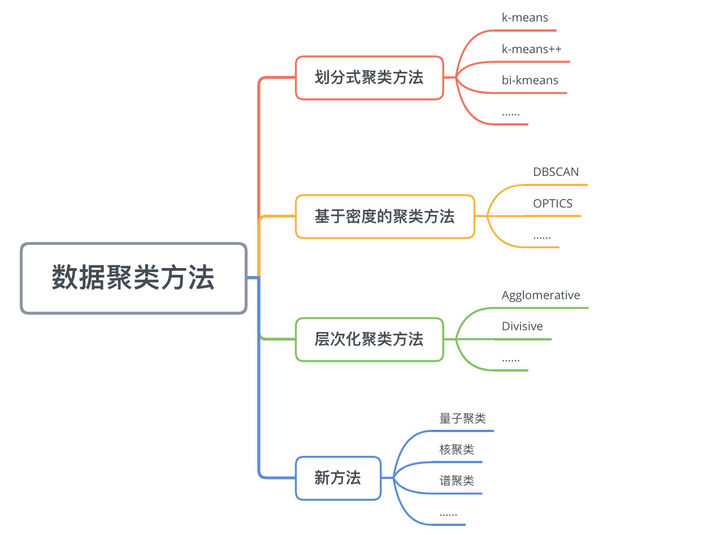
16 有监督、半监督和无监督学习(参考链接)
16.1 有监督学习
[训练集](https://so.csdn.net/so/search?q=%E8%AE%AD%E7%BB%83%E9%9B%86&spm=1001.2101.3001.7020)的每一个数据已经有特征和标签(我们在进行文本分类的时候,训练数据为已经分好类别的语料)<br />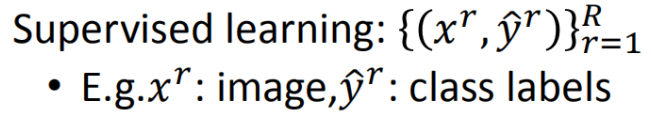<br /> 有输入数据和输出数据通过学习训练集中输入数据和输出数据的关系,生成合适的函数,将输入映射到合适的输出。比如分类、回归。
16.2 半监督学习
训练集中一部分数据有特征和标签,另一部分只有特征(只有输入没有输出),综合两类数据来生成合适的函数。【通常无标签的数据要多于有标签的数据】<br />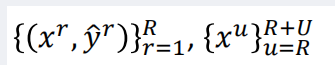
16.2.1 为什么要用半监督学习?
16.2.2 为什么半监督学习有用?
16.3 无监督学习
训练集中的数据只有特征(只有输入没有输出),通过这类数据来生成合适的函数。