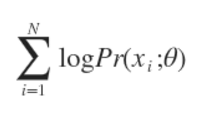机器学习

最大似然估计

最大似然估计。假设有N个数据点，服从某种分布Pr(x;θ)，我们想找到一组参数θ，使得生成这些数据点的概率最大，这个概率就是

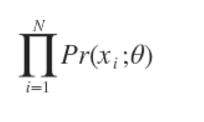
通常单个点的概率很小，连乘之后数据会更小，容易造成浮点数下溢，所以一般取其对数，变成

EM 算法

EM 算法是一种迭代算法，1977 年由 Dempster 等人总结提出，用于含有隐变量（Hidden variable）的概率模型参数的最大似然估计。
每次迭代包含两个步骤：

1. E-step：求期望 for all
2. M-step：求极大，计算新一轮迭代的模型参数

SVM&SVR&SVC

Support Vector Machine(SVM)：求一个间隔最大的划分超平面。
Support Vector Regression(SVR)：找出分类面，解决分类问题.
Support Vector Classification(SVC): 做曲线拟合、函数回归 ，做预测，温度，天气，股票.

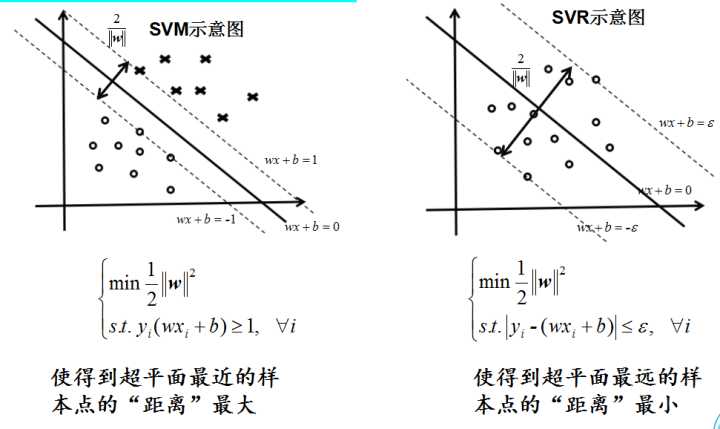
SVM基本式推导

在超平面上对样本进行分类，对于，有如下等式：

对于超平面上任意一点到超平面的距离为：

两个异类支持向量到超平面的距离之和，也称为间隔（margin），为

将找到一个最好的划分超平面转换为了找到样本空间里的最大化间隔的问题。
为了最大化间隔，仅需最大化 ，这等价于最小化 。于是上式我们可以重写为

这就是SVM的基本型。

KL 散度

Kullback-Leibler Divergence：KL 散度，这是一个用来衡量两个概率分布的相似性的一个度量指标

KL 散度，最早是从信息论里演化而来的，所以在介绍 KL 散度之前，我们要先介绍一下信息熵。信息熵的定义如下：

表示事件发生的概率.
在信息熵的基础上，我们定义 KL 散度为：

表示的就是概率 与概率 之间的差异，很显然，散度越小，说明 概率 与概率 之间越接近，那么估计的概率分布于真实的概率分布也就越接近.

H 散度

H divergence:所谓散度就是一个弱化的距离，他不一定具备距离的性质，比如有可能不满足对称性等等，那么所谓H是定义在假设空间的和的距离：

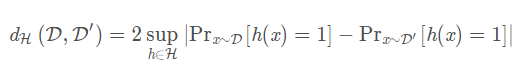
′ 直观来看，这个散度的意思是，在一个假设空间 中，找到一个函数h，使得的概率尽可能大，而的概率尽可能小，也就是说，我们用最大距离来衡量,之间的距离。同时这个h也可以理解为是用来尽可能区分,这两个分布的函数。
参考： Domain Adaptation理论分析

Kmeans

数据之间的相似度可以使用欧氏距离度量
算法步骤如下：

1. 根据设定的聚类数 K，随机地选择 K 个聚类中心（Cluster Centroid）
2. 评估各个样本到聚类中心的距离，如果样本距离第 i 个聚类中心更近，则认为其属于第 i 簇
3. 计算每个簇中样本的平均（Mean）位置，将聚类中心移动至该位置

重复以上步骤直至各个聚类中心的位置不再发生改变。
伪代码如下：

function K-Means(输入数据，中心点个数K)
    获取输入数据的维度Dim和个数N
    随机生成K个Dim维的点
    while(算法未收敛)
        对N个点：计算每个点属于哪一类。
        对于K个中心点：
            1，找出所有属于自己这一类的所有数据点
            2，把自己的坐标修改为这些数据点的中心点坐标
    end
    输出结果：
end

高斯混合模型（GMM）

最大似然估计，高斯分布，高斯混合模型，EM算法
https://zhuanlan.zhihu.com/p/30483076
高斯模型
当样本数据 X 是一维数据（Univariate）时，高斯分布遵从下方概率密度函数（Probability Density Function）：

其中 为数据均值（期望）， 为数据标准差（Standard deviation）。
当样本数据 X 是多维数据（Multivariate）时，高斯分布遵从下方概率密度函数：

高斯混合模型
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型，这 K 个子模型是混合模型的隐变量（Hidden variable）。一般来说，一个混合模型可以满足任何概率分布，这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。

• 表示第 个观测数据，
• 是混合模型中子高斯模型的数量，
• 是观测数据属于第 个子模型的概率， ，
• 是第 个子模型的高斯分布密度函数， 。其展开形式与上面介绍的单高斯模型相同

对于这个模型而言，参数 ，也就是每个子模型的期望、方差（或协方差）、在混合模型中发生的概率。

统计学习

朴素贝叶斯法

基于条件的贝叶斯公式：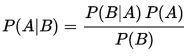

这里叫做先验概率，是条件概率，是后验概率，这三个是贝叶斯统计三要素。
在分类问题中也有别的更明朗的表达：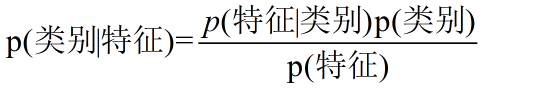

在贝叶斯分类中，对于给定的输入，通过学习模型计算后验概率分布,将后验概率最大化的类作为输出.
后验概率最大化等价于期望风险最小化。具体推导可参考《统计学习方法》

参考： 带你理解朴素贝叶斯分类算法
李航《统计学习方法》

Dirichlet Distribution

什么是狄利克雷分布？狄利克雷过程又是什么
狄利克雷分布(Dirichlet Distribution)
如何通俗理解 beta 分布？

PCA

决策树

HOG方向梯度直方图

SVM

传统检测算子

Conditional Random Field(CRF)