01背包

  • 题意：n个物品，每一个物品只能选一次，体积不超过m能得到的最大价值。

  • 状态方程：

  1. f[i][j]=f[i-1][j];//放不下的情况 
  2. if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//第i个物品选不选
  • 代码：
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define endl '\n'
  4. const int N=1010;
  5. int f[N][N];
  6. int v[N],w[N];
  7. int n,m;
  8. int main(){
  9.     cin>>n>>m;
  10.     for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
  11.     for(int i=1;i<=n;i++){
  12.         for(int j=1;j<=m;j++){
  13.             f[i][j]=f[i-1][j];//放不下的情况 
  14.             if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//第i个物品选不选 
  15.         }
  16.     }
  17.     cout<<f[n][m]<<endl;
  18. }

一维01背包代码

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define endl '\n'
  5. const int N=1010;
  7. int f[N];
  8. int v[N],w[N];
  9. int n,m;
  10. int main(){
  11.     cin>>n>>m;
  12.     for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
  13.     for(int i=1;i<=n;i++){
  14.         for(int j=m;j>=v[i];j--){
  15.             f[j]=max(f[j-v[i]]+w[i],f[j]);
  16.         }
  17.     }
  18.     cout<<f[m]<<endl;
  19. }

完全背包

  • 题意：n种物品，每种物品无限多个，求体积不超过m的最大价值。
  • 动态转移方程：
  1. f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w ,  f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
  2. f[i , j-v]= max(            f[i-1,j-v]   ,  f[i-1,j-2*v] + w , f[i-1,j-2*v]+2*w , .....)
  3. 由上两式，可得出如下递推关系： 
  4.                         f[i][j]=max(f[i,j-v]+w , f[i-1][j])
  • 代码：
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. int n,m,k,V;
  4. int a[N];
  5. int v[N],w[N];//v代表体积，w代表质量
  6. int f[N][N]; //在前i个中选，体积不超过j的最大值
  7. int main(){
  8.     cin>>n>>m;
  9.     for(int i=1;i<=n;i++){
  10.         cin>>v[i]>>w[i];
  11.     }
  12.     for(int i = 1 ; i <=n ;i++)
  13.     for(int j = 0 ; j <=m ;j++)
  14.     {
  15.         f[i][j] = f[i-1][j];
  16.         if(j-v[i]>=0)
  17.         f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
  18.     }
  19.     cout<<f[n][m]<<endl;
  20.     return 0;
  21. }

多重背包

最朴素的做法，枚举选多少个第i个物品，个数有限。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int N = 110;
  4. int n, m;
  5. int v[N], w[N], s[N];
  6. int f[N][N];
  7. int main()
  8. {
  9.     cin >> n >> m;
  11.     for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];
  13.     for (int i = 1; i <= n; i ++ )
  14.         for (int j = 0; j <= m; j ++ )
  15.             for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
  16.                 f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
  18.     cout << f[n][m] << endl;
  19.     return 0;
  20. }

多重背包有一个二进制的优化，
很菜，目前看不懂

分组背包

每一组中只能选择一个，问体积不超过m的最大值。

  2. #include<bits/stdc++.h>
  3. using namespace std;
  5. const int N=110;
  6. int f[N][N];  //只从前i组物品中选，当前体积小于等于j的最大值
  7. int v[N][N],w[N][N],s[N];   //v为体积，w为价值，s代表第i组物品的个数
  8. int n,m,k;
  10. int main(){
  11.     cin>>n>>m;
  12.     for(int i=1;i<=n;i++){
  13.         cin>>s[i];
  14.         for(int j=0;j<s[i];j++){
  15.             cin>>v[i][j]>>w[i][j];  //读入
  16.         }
  17.     }
  19.     for(int i=1;i<=n;i++){
  20.         for(int j=0;j<=m;j++){
  21.             f[i][j]=f[i-1][j];  //不选
  22.             for(int k=0;k<s[i];k++){
  23.                 if(j>=v[i][k])     f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);  
  24.             }
  25.         }
  26.     }
  27.     cout<<f[n][m]<<endl;
  28. }

线性dp

转态转移方程通常是线性的。

数字三角形

  • 状态方程：
  1. //每一个状态都可以由他左上角和上方转移
  2. f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);

代码：

  1. //这个题目也可以采用逆序的处理，不用处理边界
  2. #include<bits/stdc++.h>
  3. using namespace std;
  4. int a[1010][1010];
  5. int f[1010][1010];
  6. int n;
  7. int main(){
  8.     cin>>n;
  9.     for(int i=1;i<=n;i++){
  10.         for(int j=1;j<=i;j++){
  11.             cin>>a[i][j];
  12.         }
  13.     }
  14.     for(int i=1;i<=n;i++){
  15.         for(int j=0;j<=i+1;j++){//初始化，注意边界初始化，因为当遍历到最右边的点时可能判断得到。
  16.             f[i][j]=-1e9;
  17.         }
  18.     }
  19.     f[1][1]=a[1][1];
  20.     for(int i=2;i<=n;i++){
  21.         for(int j=1;j<=i;j++){
  22.             f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);
  23.         }
  24.     }
  25.     int ans=-1e9;
  26.     for(int i=1;i<=n;i++) ans=max(ans,f[n][i]);//问的是到最后一行的和最大值是多少。
  27.     cout<<ans<<endl;
  28. }

最长上升子序列

  • 题意：给一个长度为N的数列，问严格单调递增的子序列的长度最长是多少。
  • 转移方程：
  1. f[i] = max(f[i], f[j] + 1);
  • 代码：
  1. #include <iostream>
  2. using namespace std;
  3. const int N = 1010;
  4. int n;
  5. int w[N], f[N];
  6. int main() {
  7.     cin >> n;
  8.     for (int i = 0; i < n; i++) cin >> w[i];
  9.     int mx = 1;    // 找出所计算的f[i]之中的最大值，边算边找
  10.     for (int i = 0; i < n; i++) {
  11.         f[i] = 1;    // 设f[i]默认为1，找不到前面数字小于自己的时候就为1
  12.         for (int j = 0; j < i; j++) {
  13.             if (w[i] > w[j]) f[i] = max(f[i], f[j] + 1);    // 前一个小于自己的数结尾的最大上升子序列加上自己，即+1，如果是非递减可以改成>=
  14.         }
  15.         mx = max(mx, f[i]);
  16.     }
  17.     cout << mx << endl;
  18.     return 0;
  19. }

最长上升子序列II

  • 相比上一题，题意是一样的的，但是数据范围更强了，DP的做法DP基础 - 图1#card=math&code=O%28n%5E2%29),会超时。

  • 数据范围DP基础 - 图2

  • 思路：这一题贪心+二分 DP基础 - 图3#card=math&code=O%28nlogn%29)

我们可以用一个数组DP基础 - 图4,记录当前长度的上升序列的最后一位的最小值，维护这个数组使他最长，这部分就是贪心的策略，只有让前一位的最小，后面才能接上更多的数，让上升序列的长度更大，最后这个数组的长度就是答案。
我们可以分成两种情况：

  1. 如果接下来的数DP基础 - 图5,那么他就可以直接接到数组的最后，长度+1；
  2. 如果接下来的数DP基础 - 图6,那么就找到DP基础 - 图7中第一个大于DP基础 - 图8的数DP基础 - 图9,并将DP基础 - 图10更新为DP基础 - 图11;

代码：

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int  N=1000010;
  4. int a[N],f[N];
  5. int n,cnt=0;
  7. int find(int x){//f[cnt]是一个单调递增的数组所以可以采用二分查找。
  8.     int l=1,r=cnt;
  9.     while(l<r){
  10.         int mid=(l+r)>>1;
  11.         if(f[mid]>=x) r=mid;
  12.         else l=mid+1;
  13.     }
  14.     return  l;
  15. } 
  16. int main(){
  17.     ios::sync_with_stdio(false);
  18.     cin>>n;
  19.     for(int i=1;i<=n;i++) cin>>a[i];
  20.     f[++cnt]=a[1];
  21.     for(int i=2;i<=n;i++){
  22.         if(a[i]>f[cnt]) f[++cnt]=a[i];//大于最后一个最小的值，那么就直接加在最后面。
  23.         else {
  24.             int temp=find(a[i]);//更新前面的值，保存最小的那个值
  25.             f[temp]=a[i];
  26.         }
  27.     }
  28.     cout<<cnt<<endl;
  29.     return 0;
  30. }

最长公共子序列

  • 题意：给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
  • 动态转移方程：

图片标题

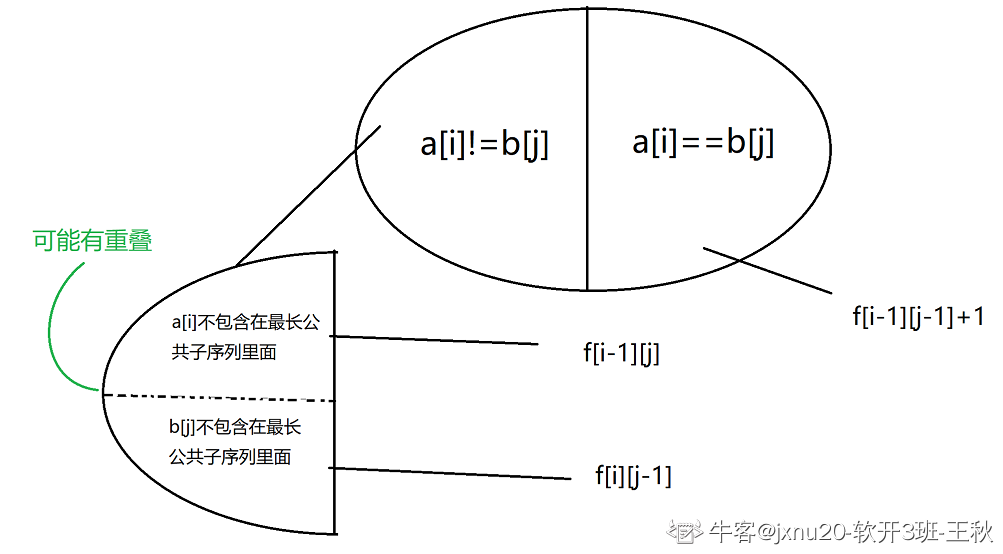
  1. if(a[i]==b[j])   f[i][j]=f[i-1][j-1]+1;
  2. else             f[i][j]=max(f[i-1][j],f[i][j-1]);
  • 代码 ：
    时间、空间复杂度：DP基础 - 图13#card=math&code=O%28n%5E2%29)
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. const int N=10010;
  5. char a[N],b[N];
  6. int f[N][N];
  8. int main(){
  9.     int n,m;
  10.     cin>>n>>m>>a+1>>b+1;
  11.     for(int i=1;i<=n;i++){
  12.         for(int j=1;j<=m;j++){
  13.            if(a[i]==b[j]) f[i][j]=f[i-1][j-1]+1;
  14.            else {
  15.                f[i][j]=max(f[i-1][j],f[i][j-1]);
  16.            }
  17.         }
  18.     }
  19.     cout<<f[n][m]<<endl;
  20.     return 0;    
  21. }

最短编辑距离

图片标题

思路

状态表示

DP基础 - 图15

表示1~ a[i],编辑成1~ b[j]的最小操作步数

状态转移方程

三种操作：
1.删除操作
DP基础 - 图16
2.插入操作
DP基础 - 图17
3.替换操作
DP基础 - 图18

代码

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define bug(x) cerr<<#x<<" : "<<x<<endl;
  4. const int N=1e3+20;
  5. const int mod=1e9+7;
  6. const int INF=2e9;
  7. typedef long long ll;
  10. char a[N],b[N];
  11. int n,m,dp[N][N];
  15. int main(){
  16.     //int T;cin>>T;while(T--){}
  17.     scanf("%d",&n);
  18.     scanf("%s",a+1);
  19.     scanf("%d",&m);
  20.     scanf("%s",b+1);
  22.     for(int i=1;i<=n;i++){
  23.         for(int j=1;j<=m;j++){
  24.             dp[i][j]=INF;//因为要去最小值，应该赋初值为极大值，不然会出问题
  25.         }
  26.     }
  27.     for(int i=1;i<=n;i++) dp[i][0]=i;//处理边界，
  28.     for(int i=1;i<=m;i++) dp[0][i]=i;
  31.     for(int i=1;i<=n;i++){
  32.         for(int j=1;j<=m;j++){
  33.             dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//插入、删除
  34.             if(a[i]==b[j]) dp[i][j]=min(dp[i-1][j-1],dp[i][j]);
  35.             else dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);//替换
  36.         }
  37.     }
  38.     cout<<dp[n][m]<<endl;
  40. }
  42. /*
  43. 状态表示
  44. dp[i][j]
  45. 表示1~a[i],编辑成1~b[j]的最小操作步数
  47. 状态转移方程
  48. 三种操作：
  49. 1.删除操作
  50. dp[i][j]=dp[i-1][j]+1;
  51. 2.插入操作
  52. dp[i][j]=dp[i][j-1]+1;
  53. 3.替换操作
  54. dp[i][j]=dp[i-1][j-1]+1;
  55.  */

区间DP

石子合并

题意：合并 N 堆石子，每次只能合并相邻的两堆石子，求最小代价。

思路：
合并一定是左边连续的一部分，和右边连续的一部分进行合并。

状态表示：
DP基础 - 图19表示合并DP基础 - 图20堆的石子所需要花费的最小体力。
属性：Min
状态转移方程：
当DP基础 - 图21时，DP基础 - 图22
当DP基础 - 图23时，DP基础 - 图24
时间复杂度：DP基础 - 图25#card=math&code=O%28n%5E%7B3%7D%29)

代码：

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. #define bug(x) cerr<<#x<<" : "<<x<<endl;
  4. #define x first
  5. #define y second
  6. const int N=2e3+10; 
  7. typedef long long ll;
  9. int a[N],s[N];
  11. int f[N][N];
  13. int main(){
  14.     int n;
  15.     cin>>n;
  16.     for(int i=1;i<=n;i++){
  17.         cin>>a[i];
  18.         s[i]=s[i-1]+a[i];//求前缀和，求合并i~j堆石子的消耗体力 
  19.     }
  20.     for(int len=1;len<=n;len++){
  21.         for(int i=1;i+len<=n;i++){
  22.             int j=i+len;
  23.             f[i][j]=1e9;
  24.             for(int k=i;k<=j-1;k++){
  25.                  f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
  26.             }
  27.         }
  28.     }
  29.     cout<<f[1][N]<<endl;
  31. }

区间DP模板：

  1. for (int i = 1; i <= n; i++) {
  2.     dp[i][i] = 初始值
  3. }
  4. for (int len = 2; len <= n; len++)           //区间长度
  5.     for (int i = 1; i + len - 1 <= n; i++) { //枚举起点
  6.         int j = i + len - 1;                 //区间终点
  7.         for (int k = i; k < j; k++) {        //枚举分割点，构造状态转移方程
  8.             dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
  9.         }
  10.    }

数位DP

计数问题

求a~b，1 ~ 9各出现了多少次。

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. #define bug(x) cerr<<#x<<" : "<<x<<endl;
  4. #define x first
  5. #define y second
  6. const int N=2e4+10; 
  7. const int mod=1e9+7;
  8. typedef long long ll;
  10. int dgt(int n){
  11.     int res=0;
  12.     while(n){
  14.         res++;
  15.         n/=10;
  16.     }
  17.     return res;
  18. }
  20. int cnt(int n,int i){
  21.     int res=0,d=dgt(n);
  22.     for(int j=1;j<=d;j++){
  23.         int p=pow(10,j-1),l=n/p/10,r=n%p,dj=n/p%10;
  24.         if(i) res += l*p;
  25.         if(!i && l) res += (l-1)*p;
  26.         if( (dj > i) && (i || l)) res += p;
  27.         if( (dj == i) && (i || l)) res += r+1; 
  28.     }
  29.     return res;
  30. }
  32. int main(){
  33.     int a,b;
  34.     while(cin>>a>>b,a){
  35.         if(a>b) swap(a,b);
  36.         for(int i=0;i<=9;i++){
  37.             cout<<cnt(b,i)-cnt(a-1,i)<<" ";
  38.         }
  39.         cout<<'\n';
  40.     }
  41.     return 0;
  42. }