一、什么是HashMap?
HashMap 数据结构为 数组+链表(JDk1.7),JDK1.8中增加了红黑树,其中:链表的节点存储的是一个 Entry 对象,每个Entry 对象存储四个属性(hash,key,value,next)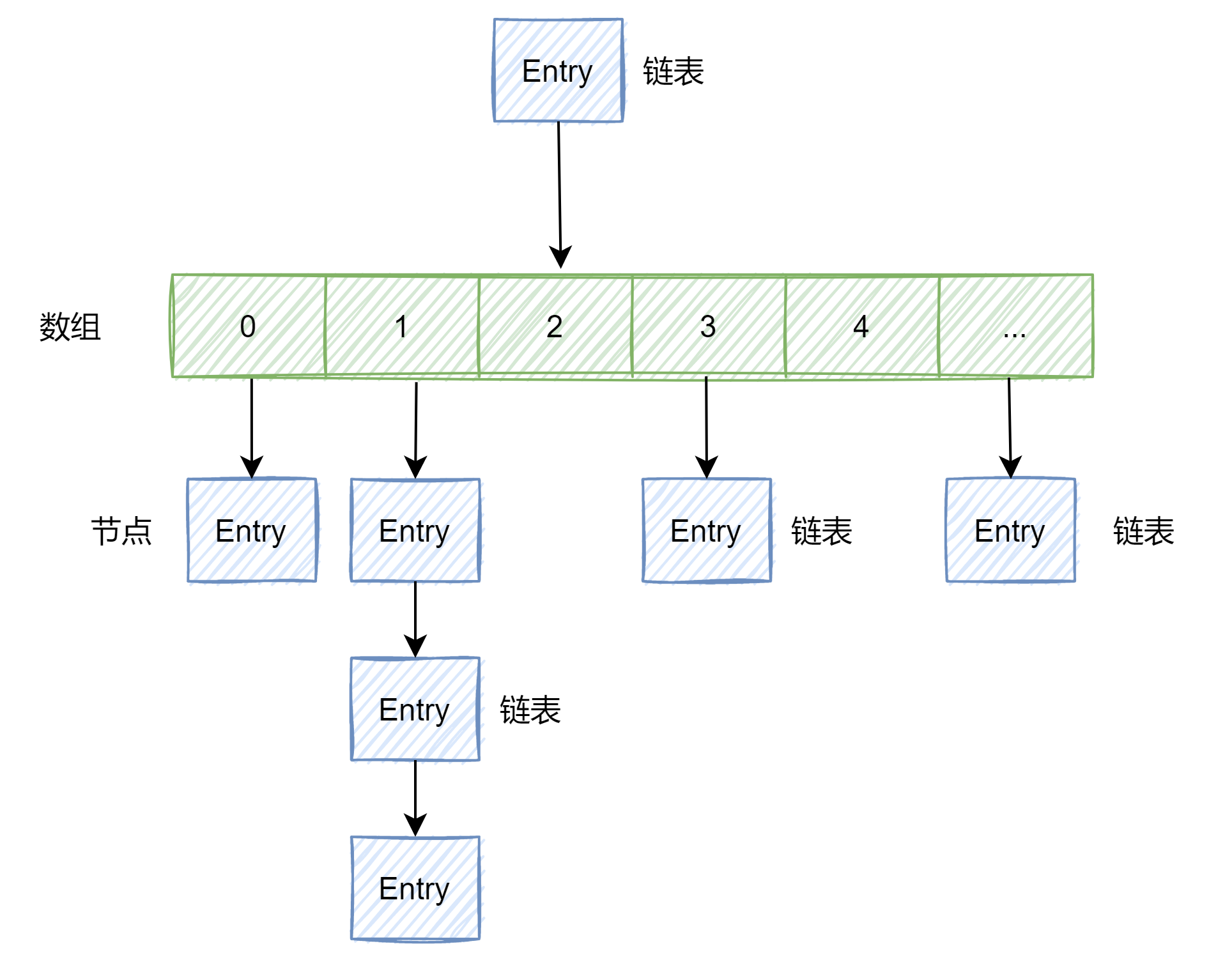
二、为什么要使用HashMap?
对于要求查询次数特别多,查询效率比较高同时插入和删除的次数比较少的情况下,通常会选择ArrayList,因为它的底层是通过数组实现的。
对于插入和删除次数比较多同时在查询次数不多的情况下,通常会选择LinkedList,因为它的底层是通过链表实现的。
但现在同时要求插入,删除,查询效率都很高的情况下我们该如何选择容器呢?
那么就有一种新的容器叫HashMap,他里面既有数组结构,也有链表结构,所以可以弥补相互的缺点。而且HashMap主要用法是get()和put() 。
三、HashMap扩容为什么总是2的次幂?
总结:因为2的N次幂的二进制是1000000000…. 而2的N次幂 - 1是0111111111…..,当hash算法得到的值与
0111111111111进行&运算的时候,只有都是1结果才为1,能够充分散列,减少hash碰撞;
HashMap的扩容公式:initailCapacity loadFactor = HashMap
其中initailCapacity是初始容量:默认值为16(懒加载机制,只有当第一次put的时候才创建)
其中loadFactor是负载因子:默认值为0.75
也就是说当16 0.75 = 12时,HashMap就会开始扩容,值得提醒的是初始容量和负载因子也可以自己设定的。 使用的是位运算进行扩容,因为用乘法会影响CPU的性能,计算机不支持乘法运算,最终都会转化为加法运算。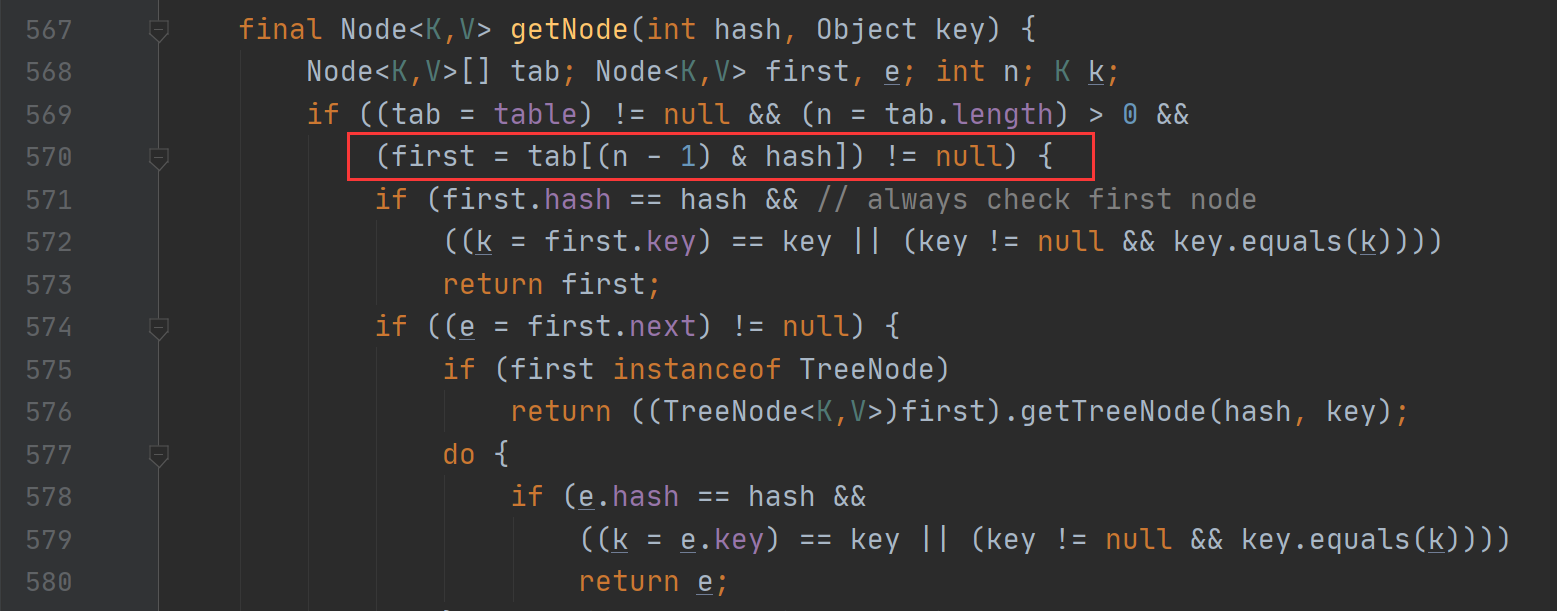
HashMap扩容主要是给数组扩容的,因为数组长度不可变,而链表是可变长度的。从HashMap的源码中可以看到HashMap在扩容时选择了位运算,向集合中添加元素时,会使用(n - 1) & hash的计算方法来得出该元素在集合中的位置。只有当对应位置的数据都为1时,运算结果也为1,当HashMap的容量是2的n次幂时,(n-1)的2进制也就是1111111*111这样形式的,这样与添加元素的hash值进行位运算时,能够充分的散列,使得添加的元素均匀分布在HashMap的每个位置上,减少hash碰撞,下面举例进行说明。
当HashMap的容量是16时,它的二进制是10000,(n-1)的二进制是01111,与hash值得计算结果如下: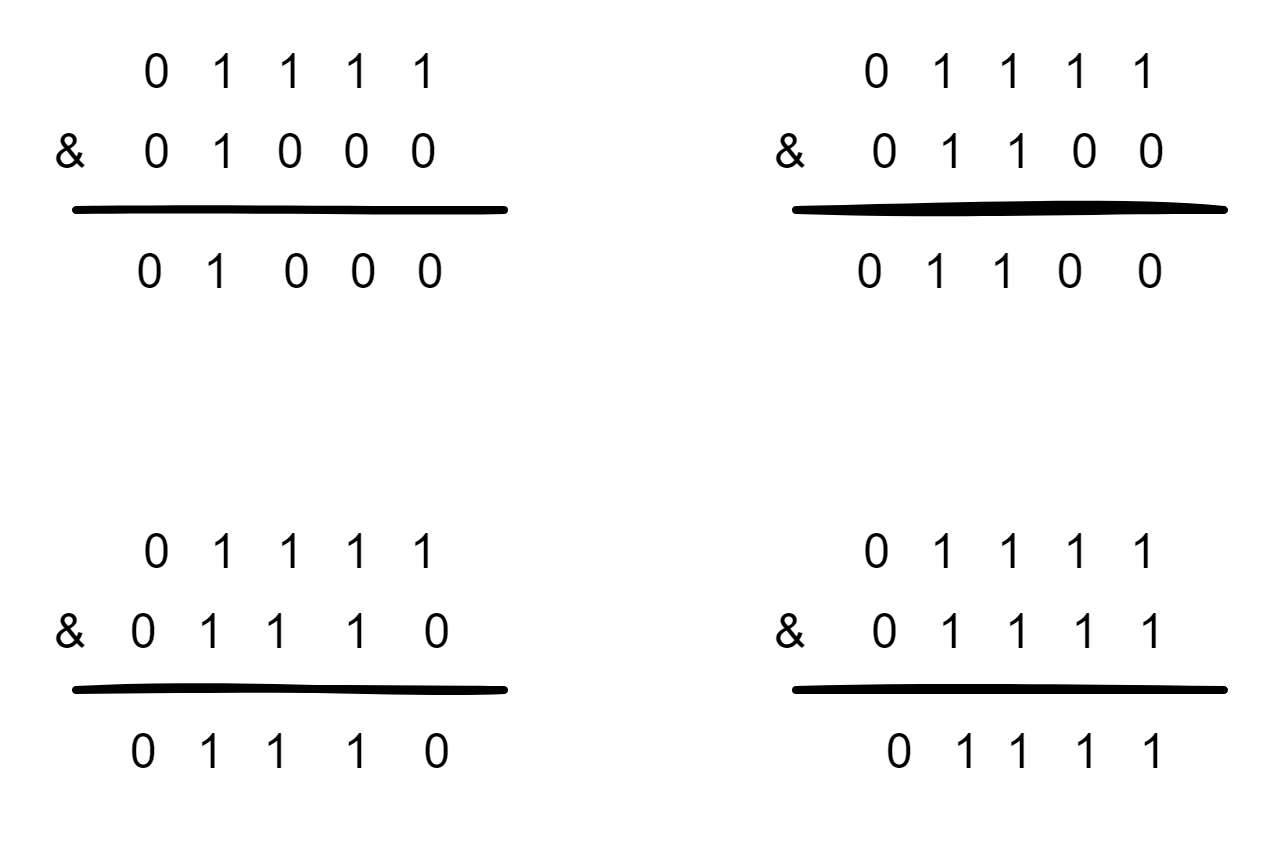
上面四种情况我们可以看出,不同的hash值,和(n-1)进行位运算后,能够得出不同的值,使得添加的元素能够均匀分布在集合中不同的位置上,避免hash碰撞。
下面就来看一下HashMap的容量不是2的n次幂的情况,当容量为10时,二进制为01010,(n-1)的二进制是01001,向里面添加同样的元素,结果为: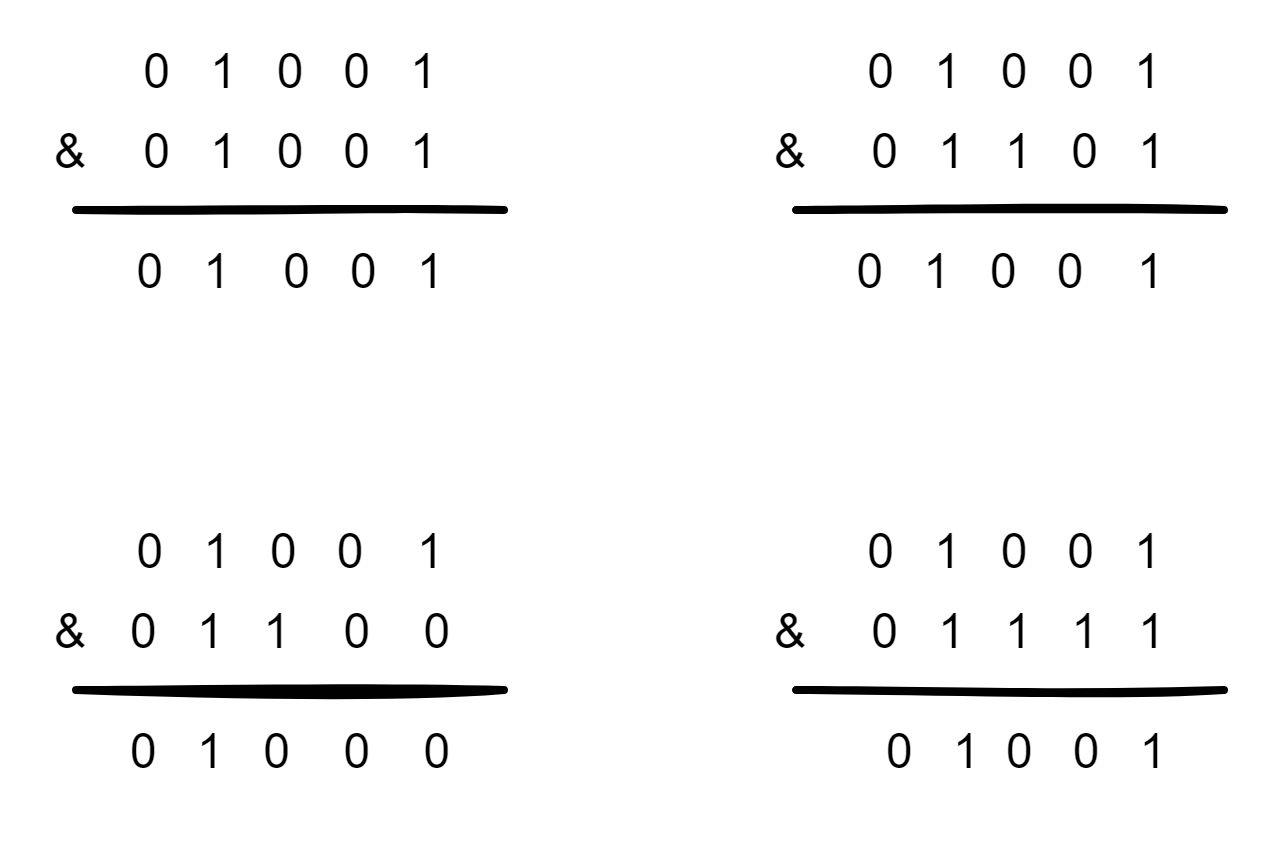
可以看出,有三个不同的元素经过&运算得出了同样的结果,严重的hash碰撞了。导致某一个链表的长度特别长,影响查询的效率。
终上所述,HashMap计算添加元素的位置时,使用的位运算,这是特别高效的运算;另外,HashMap的初始容量是2的n次幂,扩容也是2倍的形式进行扩容,是因为容量是2的n次幂,可以使得添加的元素均匀分布在HashMap中的数组上,减少hash碰撞,避免形成链表的结构,使得查询效率降低!
有个问题:为啥不使用取模呢?因为取模运算速度比较低。
四、JDk1.7HashMap扩容死循环问题
HashMap是一个线程不安全的容器,在最坏的情况下,所有元素都定位到同一个位置,形成一个长长的链表,这样get一个值时,最坏情况需要遍历所有节点,性能变成了O(n)。
JDK1.7中HashMap采用头插法拉链表,所谓头插法,即在每次都在链表头部(即桶中)插入最后添加的数据。
死循环问题只会出现在多线程的情况下。
假设在原来的链表中,A节点指向了B节点。
在线程1进行扩容时,由于使用了头插法,链表中B节点指向了A节点。
在线程2进行扩容时,由于使用了头插法,链表中A节点又指向了B节点。
在线程n进行扩容时,…
这就容易出现问题了。。在并发扩容结束后,可能导致A节点指向了B节点,B节点指向了A节点,链表中便有了环!!!
导致的结果:CPU占用率100%
五、JDK1.8的新结构——红黑树
为了解决JDK1.7中的死循环问题, 在jDK1.8中新增加了红黑树,即在数组长度大于64,同时链表长度大于8的情况下,链表将转化为红黑树。同时使用尾插法。当数据的长度退化成6时,红黑树转化为链表。
1.为什么非要使用红黑树呢?
这个选择是综合各种考虑之下的,既要put效率很高,同时也要get效率很高,红黑树就是其中一种。
2.什么是红黑树?
首先讲一下二叉查找树:
1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树。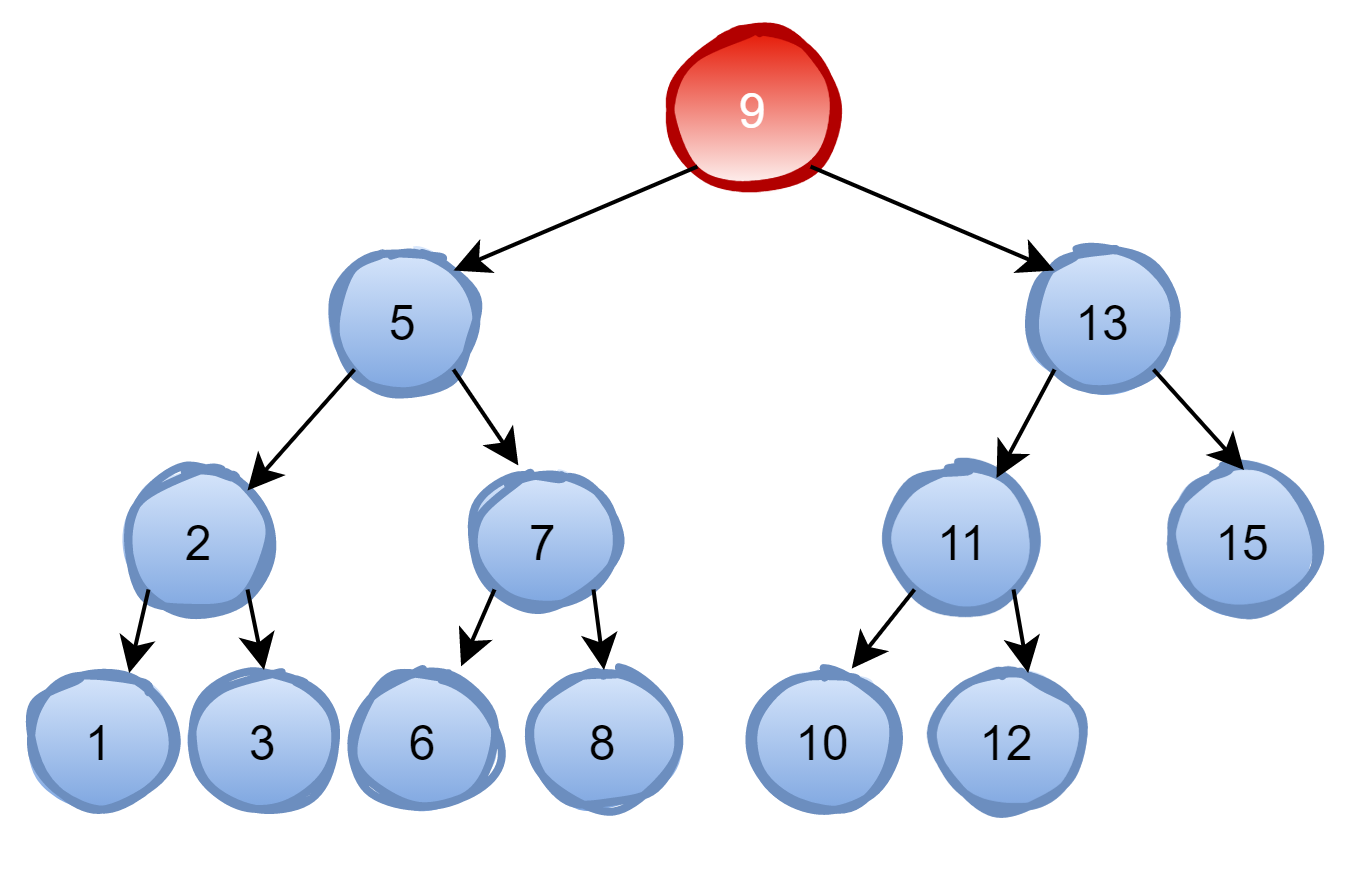
如果要查找10。先看根节点9,由于10 > 9,因此查看右孩子13;由于10 < 13,因此查看左孩子11;由于10 < 11,因此查看左孩子10,发现10正是要查找的节点;这种方式查找最大的次数等于二叉查找树的高度。 复杂度为O(log n),但是二叉查找树也有他的缺点,如果二叉树有如下的三个节点: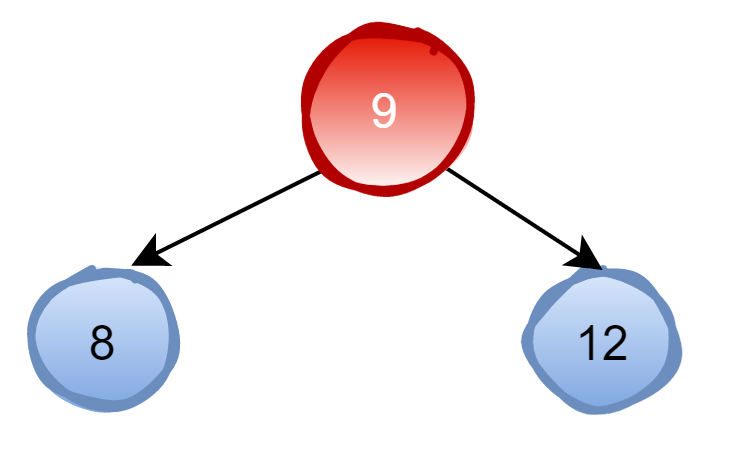
当插入7,6,5,4这四个节点时: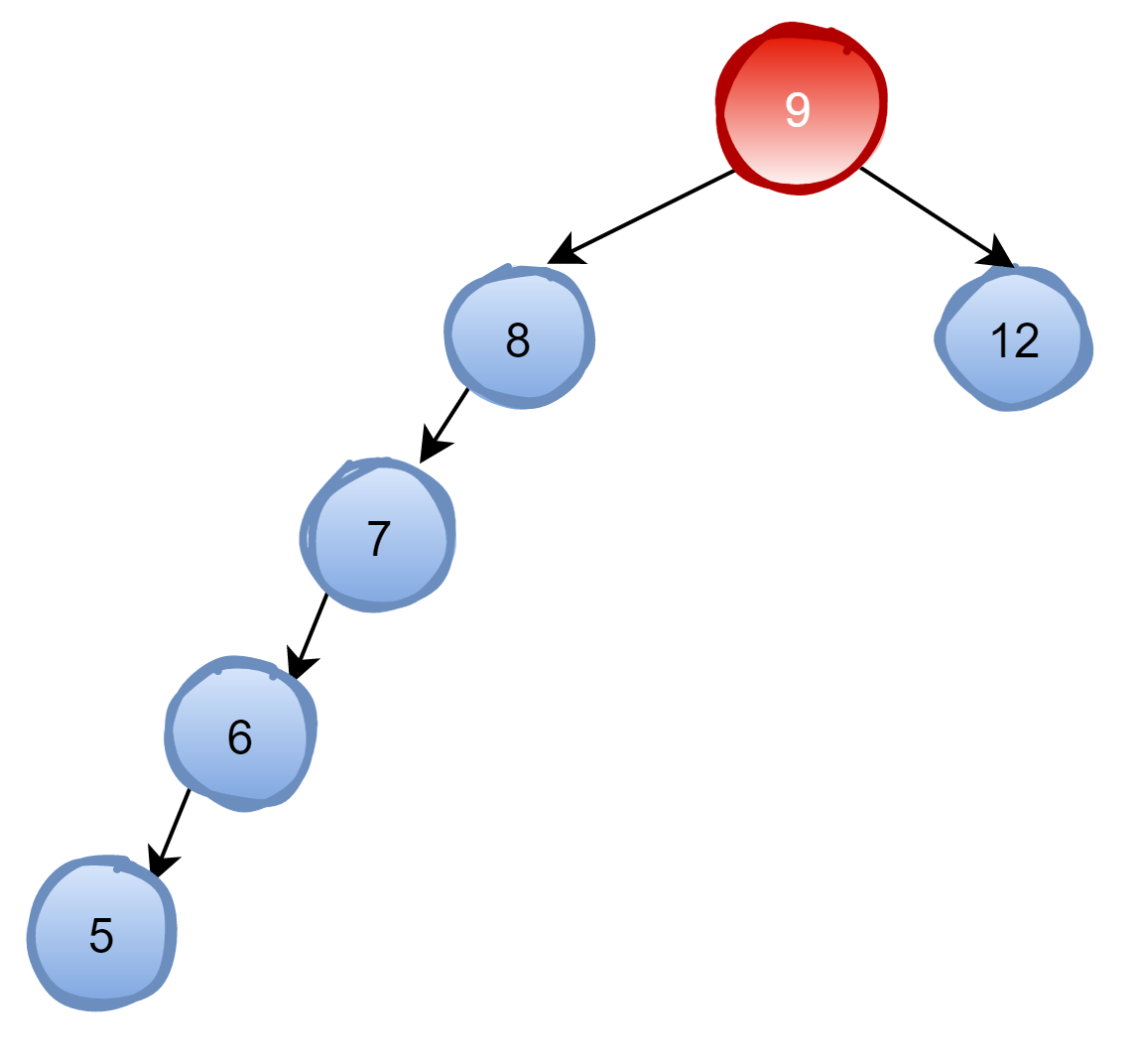
随着树的深度增加,那么查找的效率就变得非常差了,变成了O(n),就不具有二叉查找树的优点了。
那么红黑树就诞生了,红黑树是一种自平衡的二叉查找树。
3.红黑树的特性
1.节点是红色或黑色;
2.根节点是黑色;
3.每个叶子节点都是黑色的空节点(NIL节点);
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点);
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点;
6.每次新插入的节点都必须是红色。
如图就是一颗红黑树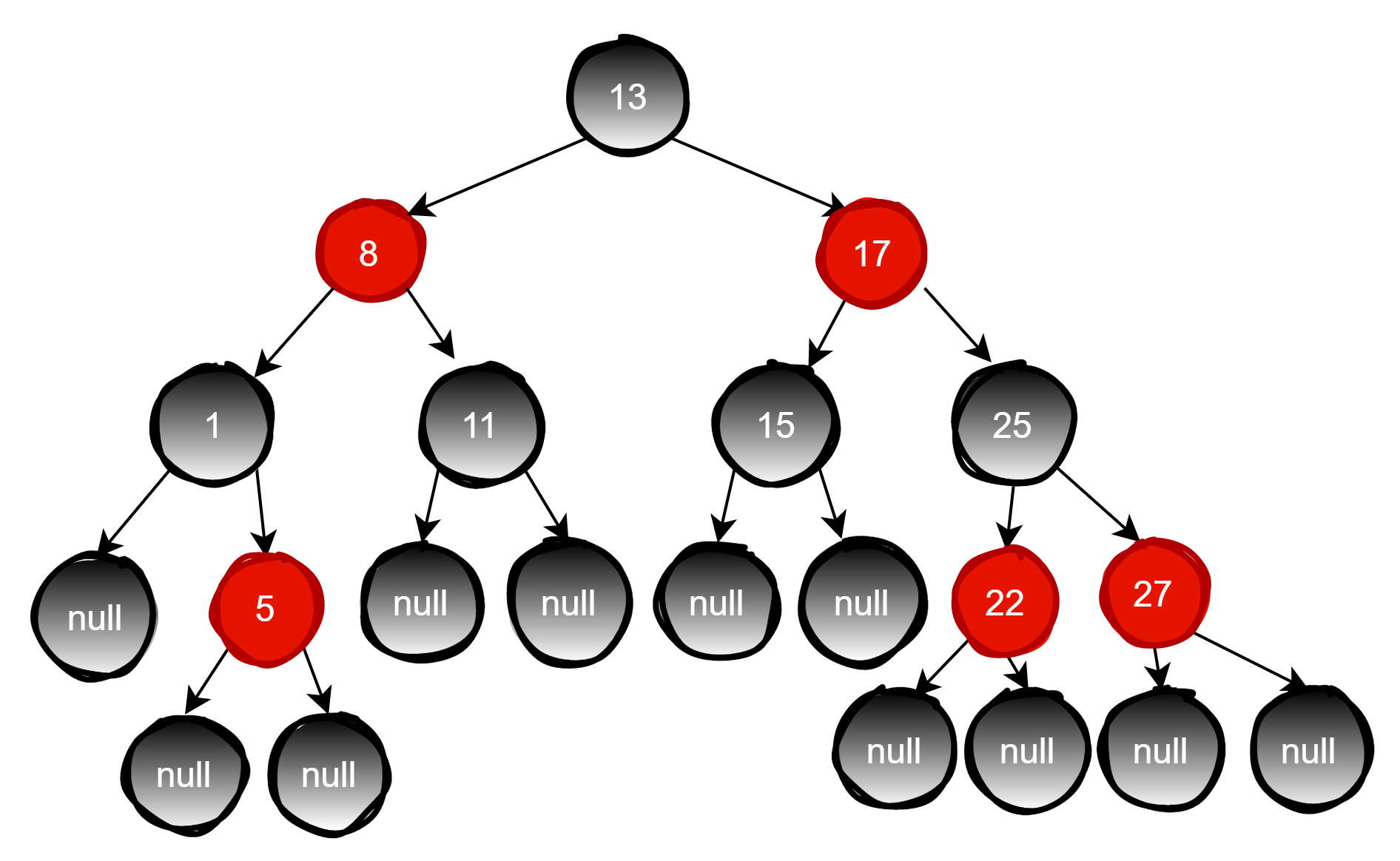
红黑树从根节点到叶子节点的最长路径不会超过最短路径的两倍。但是红黑树有时候在插入和删除过程中会破坏自己的规则,比如插入节点26,如下图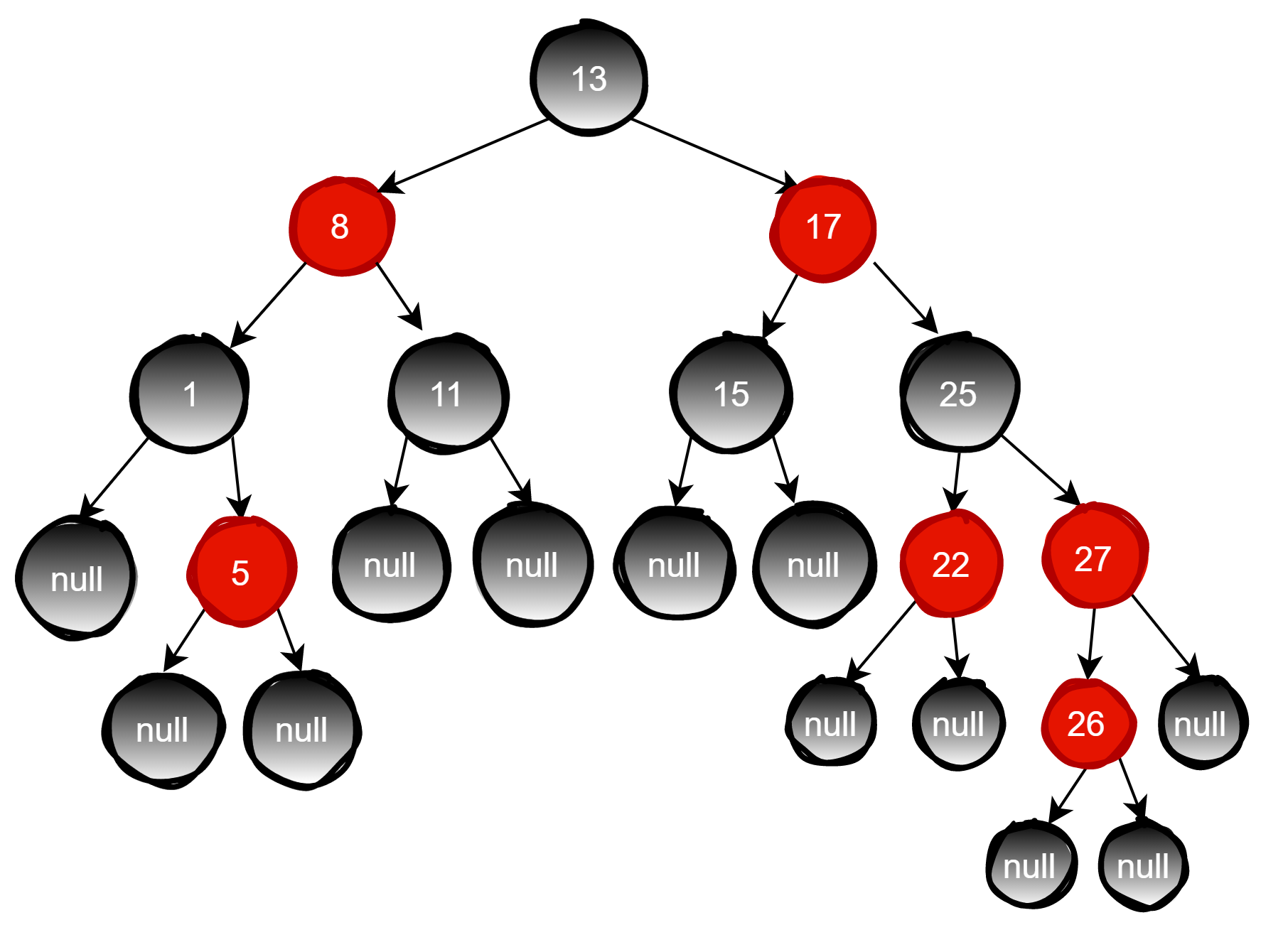
由于父节点27是红色节点,因此这种情况打破了红黑树的规则4(每个红色节点的两个子节点都是黑色),必须进行调整,使之重新符合红黑树的规则。
常用的调整方法有三种:

