一、最小路径和
给定一个包含非负整数的 _m_ x _n_ 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
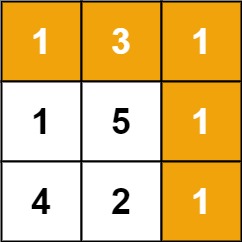
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]输出:7解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 200-
Solution:
class Solution { public int minPathSum(int[][] grid) { int m = grid.length; int n = grid[0].length; int[][] dp = new int[m][n]; dp[0][0] = grid[0][0]; for(int i = 1; i < m; i++){ dp[i][0] = dp[i-1][0] + grid[i][0]; } for(int j = 1; j < n; j++){ dp[0][j] = dp[0][j-1] + grid[0][j]; } for(int i = 1; i < m; i++){ for(int j = 1; j < n; j++){ dp[i][j] = Math.min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]); } } return dp[m-1][n-1]; } }二、打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
Solution
class Solution {
// 动态规划
public int rob(int[] nums) {
if (nums.length == 0)
return 0;
if (nums.length == 1)
return nums[0];
int n = nums.length;
int[] dp = new int[n];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < n; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[n - 1];
}
}
三、打家劫舍Ⅱ
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [0]
输出:0
提示:
1 <= nums.length <= 1000 <= nums[i] <= 1000
class Solution {
public int rob(int[] nums) {
if (nums.length == 0)
return 0;
if (nums.length == 1)
return nums[0];
if (nums.length == 2)
return Math.max(nums[0], nums[1]);
int n = nums.length;
return Math.max(robRange(nums, 0, n - 2), robRange(nums, 1, n - 1));
}
public int robRange(int[] nums, int start, int end) {
int first = nums[start], second = Math.max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
int temp = second;
second = Math.max(first + nums[i], second);
first = temp;
}
return second;
}
}
四、买卖股票的最佳时机Ⅱ
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 3 * 10<sup>4</sup>0 <= prices[i] <= 10<sup>4</sup>
Solution
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[] dpProfit = new int[n];
int[] dpState = new int[n];
dpProfit[0] = 0;
dpState[0] = -prices[0];
for (int i = 1; i < n; i++) {
// 第i天卖出股票获得最大利润
dpProfit[i] = Math.max(dpProfit[i - 1], dpState[i - 1] + prices[i]);
// 第i天买入股票损失最小利润
dpState[i] = Math.max(dpState[i - 1], dpProfit[i - 1] - prices[i]);
}
return dpProfit[n - 1];
}
}
五、杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
Solution
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> ans = new LinkedList<>();
for (int i = 0; i < numRows; i++) {
List<Integer> row = new LinkedList<>();
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) {
row.add(1);
} else {
row.add(ans.get(i - 1).get(j - 1) + ans.get(i - 1).get(j));
}
}
ans.add(row);
}
return ans;
}
}
六、杨辉三角Ⅱ
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3
输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
Solution
class Solution {
public List<Integer> getRow(int rowIndex) {
List<List<Integer>> triangle = new ArrayList<>();
for (int i = 0; i <= rowIndex; i++) {
List<Integer> row = new ArrayList<>();
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) {
row.add(1);
} else {
row.add(triangle.get(i - 1).get(j - 1) + triangle.get(i - 1).get(j));
}
}
triangle.add(row);
}
return triangle.get(rowIndex);
}
}

