参考文献 https://blog.csdn.net/Xurui_Luo/article/details/106357545 https://blog.csdn.net/Trasper1/article/details/81878892

贝叶斯公式

_

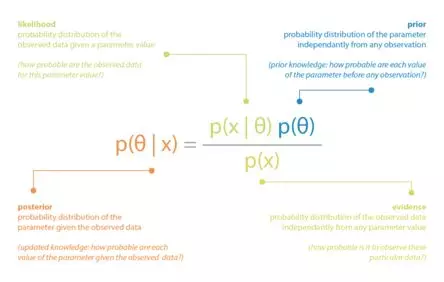
为了更有效了解贝叶斯方法，首先要对贝叶斯公式中的各项有个提前的了解。

• ：后验概率分布 Posterior
• ：似然概率分布 Likelihood
• ：先验概率分布 Prior

对贝叶斯公式的直观理解就是:

通过新一波采样得到数据 ，我们可以计算出新的 概率分布，也就是 也称对 的更新、纠正。通过这个概率分布，我们就可以得到 的值，计算方法就是求 这个分布下， 的均值。

贝叶斯派的基本思想 vs 频率学派基本思想

• 在贝叶斯理论中， 是根据你的观测在不停变的。在这个过程中，每一次的观测，得到的具体数据 则视作固定的。根据观测，会不断地更新 。
• 频率学派则相反。 是一直都固定的。无论你怎样进行采样， 都不会发生改变，因此想要求 就得利用极大似然估计。这个本文不作介绍。

解释

Prior 先验——

之前的知识，我们对它刻板印象，没有基于观测的数据思考而进行的猜测。比如这里 的分布是我们先前根据经验得来的，它的概率分布就是。

由于一般的机器学习中，是没有办法得到关于参数的先验信息的，所以一般无法直接利用先验来做一些事情

Likelihood 似然 ——

顾名思义，似然就是像这样，因此其表达式肯定看着像，但不是真的。像什么呢？就是你得到的这些观测数据，像是根据你的先验知识，估计而来而来的。其含义正是这个公式。它表示在给定 的情况下， 服从的概率分布。

那么既然只是像，哪里有问题呢？

结合之前所说， 是固定的，根本不会随着 的改变而发生任何变化。因此，这里仅仅只是似然，假装是 控制 的生成，假装 对 的分布起作用。

在许多机器学习中，用Loss值的负数来代表似然。

Posterior 后验——

在你有了观测的数据之后，得到的新参数的概率分布。正如贝叶斯的思想所言，控制事务发生概率的参数 是变化的，它会随着新的观测数据到来，不断改变。

有了它以后，可以根据概率分布求期望（均值），从而进行一些估计。

大多数机器学习中，需要对后验概率进行推测，这也是贝叶斯机器学习的目的。
**

贝叶斯分类器

贝叶斯分类器是传统机器学习模型的一种，是在概率框架下利用训练集D观测估计样本属性（feature）与分类结果之间的后验概率关系。后验概率，就是在观测过样本的属性（feature）之后对其分类情况的概率分布（比如0.3的概率是正类，0.7的概率是反类）。贝叶斯分类器直观看就是一个由在样本集D上学习到的后验概率和likelihood组成的计算公式**，在测试阶段，将输入测试样本的feature带入可以计算出各类的分类confidence（confidence即后验）**。