文章:Li S, Jiao J, Han Y, et al. Demystifying ResNet[J]. arXiv preprint arXiv:1611.01186, 2016.
贯穿文章的四个问题:
- 为什么ResNet深和浅结构训练难度是一样的,不会像其他的网络训练难度随着深度增加而递增?
- 为什么2-shortcut的结构最好?
- 为什么要用深层线性网络来说明问题?
- 为什么要零初始化?
先说结论:
- ResNet的海森矩阵计算出的条件数是和深度无关的
- 分三种情况
- 1-shortcut:即结构中只有一层weight的,此种情况条件数将随层数不断增加,反而难以脱离初始点
- 2-shortcuts:即最经典的ResNet结构,此种初始点为strict saddle point,容易脱离
- 3+-shortcuts:三层和三层以上的,此种情况下零初始点是一个高阶驻点,也不容易脱离
- 首先是线性网络,超过一层的线性网络的训练是有非线性变化的;其次线性网络不会因为其深度增加而效果变好,这一点和ResNet不同。
- 为了保证输入和输出的方差不会差别很大
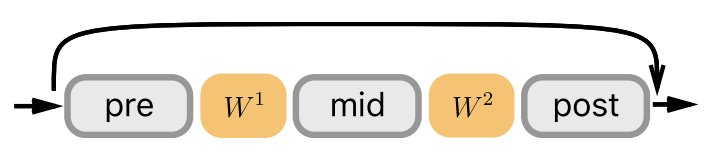
图: 2-shortcuts中间包含两层待训练参数
ResNet好,最近一直在炒,那么为啥好,众说纷纭,也没个准确的。这篇文章从条件数的角度阐述了为什么ResNet好,为什么2-shortcuts的最好。
不同于其他的方法,文章使用了线性方法,为什么用线性方法呢?
在 [1] 里面说明了,线性网络虽然堆叠没用(还是线性),但是只要隐层层数超过一层,那么就会有nonlinear dynamics of training。什么是nonlinear dynamics of training呢?简言之就是训练过程中表现出的非线性的性质。
要研究ResNet为什么好,就要从三个方面研究
- 初始情况
- 训练情况(dynamic)
- 训练结果
初始条件
好的开始是成功的一半,选择正确的初始化也会使得训练效果事半功倍。
常用的参数初始化方法包括:
- 高斯初始化:最常见的初始化方法,参数服从高斯分布
- Xavier初始化:Xavier初始化是基于这样的假设,“如果输入和输出的方差一致,那么信息传递更快”,想要做到这一点,要求初始化权重服从
- 正交初始化:仅限于CNN,其初始化就是其权重矩阵是随机正交矩阵,即满足
- 0初始化:全部取0,可能加些偏置
这里,我们选择对后面三种比较,最终选择了零初始化。理由如下
①从Xavier角度,在线性网络中可以满足
那么只要 和
满足独立同分布,就可以得到
%3DVar(x)%5Cprod%7Bi%3D1%7D%5E%7Bn%7Dn_iVar(W_i)#card=math&code=Var%28y%29%3DVar%28x%29%5Cprod%7Bi%3D1%7D%5E%7Bn%7Dn_iVar%28W_i%29&id=061d7cf1)
所以只要满足
%3D1#card=math&code=%5Cprod_%7Bi%3D1%7D%5E%7Bn%7Dn_iVar%28W_i%29%3D1&id=44d24346)
就能达到Xavier初始化的条件。
但是对于ResNet,原来的网络就变成了
x#card=math&code=y%3D%5Cprod%5ER%7Br%3D1%7D%28%5Cprod%5En%7Bl%3D1%7DW%5E%7Br%2Cl%7D%2BI%29x&id=8ad10b58)
显然,要想还有输入输出方差一致的特性,只有所有权重0初始化。
②从orthogonal角度
正交初始化的初衷就是使得初始化矩阵是正交矩阵,从而其奇异值均为1,即可保证输入和输出的方差一致,问题又回到了Xavier初始化的问题,两个方法解决的是同一个问题,只是途径不同罢了。
下面证明对于,为什么下面两个条件等价
是正交矩阵
在线性网络里面这个奇异值全部为1需要构建,而在ResNet里面,因为包含了identity mapping,不需要构建了,本身就有,那么只要把参数0初始化就可以轻松得到同样效果。
系统优化过程
损失函数
%3D%5Cfrac%7B1%7D%7B2m%7D%5Csum%5Em%7B%5Cmu%3D1%7D%7C%7Cy%5E%7B%5Cmu%7D-Wx%5E%7B%5Cmu%7D%7C%7C%5E2_2%3D%5Cfrac%7B1%7D%7B2m%7D%7C%7CY-WX%7C%7C%5E2_2#card=math&code=L%28%5Cmathbf%7Bw%7D%29%3D%5Cfrac%7B1%7D%7B2m%7D%5Csum%5Em%7B%5Cmu%3D1%7D%7C%7Cy%5E%7B%5Cmu%7D-Wx%5E%7B%5Cmu%7D%7C%7C%5E2_2%3D%5Cfrac%7B1%7D%7B2m%7D%7C%7CY-WX%7C%7C%5E2_2&id=50f2aceb)
使用梯度下降法,我们想要求出其每次更新权重。
关于$W$可以写成关于某一层(第
个residual unit里面的第
个权重矩阵)的形式,注意,仅限于线性连接
W%5Er%7Bafter%7D#card=math&code=W%3DW%5Er%7Bbefore%7D%28W%5E%7Br%2Cl%7D%7Bbefore%7DW%5E%7Br%2Cl%7DW%5E%7Br%2Cl%7D%7Bafter%7D%2BI%7Bd_x%7D%29W%5Er%7Bafter%7D&id=318ee4ec)
那么利用损失函数,求取关于
的导数
可以得到
%5ET(%5CSigma%5E%7BYX%7D-W%5CSigma%5E%7BXX%7D)(W%5E%7Br%2Cl%7D%7Bbefore%7DW%5Er%7Bbefore%7D)%5ET#card=math&code=%5CDelta%20W%5E%7Br%2Cl%7D%3D%5Calpha%28W%5Er%7Bafter%7DW%5E%7Br%2Cl%7D%7Bafter%7D%29%5ET%28%5CSigma%5E%7BYX%7D-W%5CSigma%5E%7BXX%7D%29%28W%5E%7Br%2Cl%7D%7Bbefore%7DW%5Er%7Bbefore%7D%29%5ET&id=5c41d035)
其中和
分别代表input-output相关矩阵和input-input相关矩阵,其表达式如下
%5ET#card=math&code=%5CSigma%5E%7BYX%7D%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em_%7B%5Cmu%3D1%7Dy%5E%7B%5Cmu%7D%28x%5E%7B%5Cmu%7D%29%5ET&id=caff9a1a)
%5ET#card=math&code=%5CSigma%5E%7BXX%7D%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em_%7B%5Cmu%3D1%7Dx%5E%7B%5Cmu%7D%28x%5E%7B%5Cmu%7D%29%5ET&id=19b67088)
0初始化中的条件数
关于为什么要0初始化,在前面已经说明了,那么,我们就要就第一个问题,初识情况来分析ResNet。
要想求条件数,那么首先就要构建海森矩阵,其一般式如下
%2Cind(w2)%7D%3D%5Cfrac%7B%5Cpartial%5E2L%7D%7B%5Cpartial%20w_1%5Cpartial%20w_2%7D#card=math&code=H%7Bind%28w_1%29%2Cind%28w_2%29%7D%3D%5Cfrac%7B%5Cpartial%5E2L%7D%7B%5Cpartial%20w_1%5Cpartial%20w_2%7D&id=99a80859)
对于一个权重值,必然是包含4个小index的,分别是
① :所在residual unit的编号;
② :residual unit里面权重矩阵的编号;
③ :所处权重矩阵的行;
④ :所处权重矩阵的列。
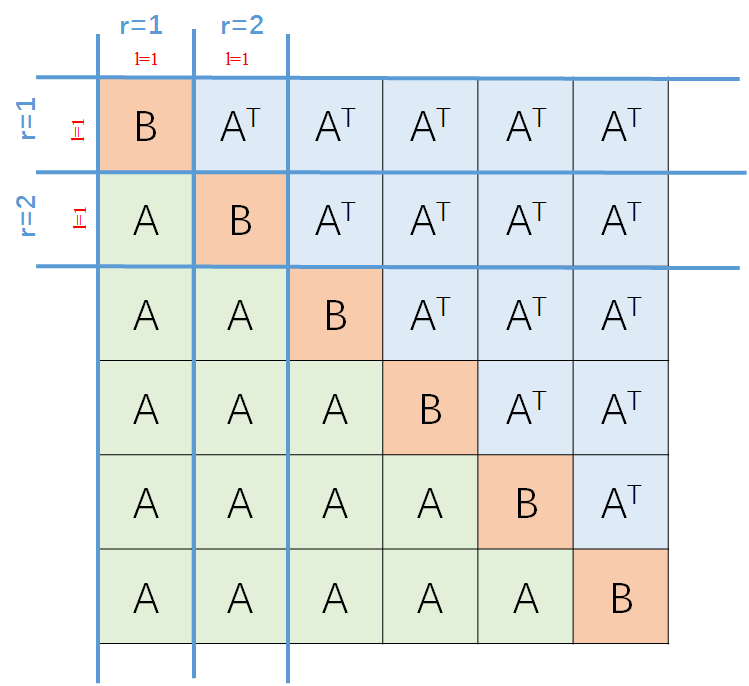
按这四个index将所有权重拉成一条直线,于是就可以得到海森矩阵如下图(假设2-shortcuts)
2+-shortcuts
那么首先从$n\ge 3$说起,此时,取0初始化,这个0点就是损失函数的$n-1$阶驻点。
要了解这个首先从驻点说起。什么是驻点,搬个定义
驻点:函数的一阶导数为0的点
n阶驻点:函数的n阶导数为0的点,意即则
是
的
阶驻点。
那么对于海森矩阵,其中的每一个元素都是关于损失函数L的二阶偏导。
引入定理1:
从n-shortcuts的网络里面,任取N个权重
,假如
对这
个权重的
阶偏导不为0,即
,那么这
个权重中肯定存在
个权重是分别属于一个residual unit里的
个权重矩阵的。
先不考虑证明,定理1说明了什么呢?
首先,N阶偏导不为0,那么在0点的时候就不是L的驻点。其次,一定要最少有n个权重,n-1个就是0,也就是说对于L来说这是个n-1阶驻点。当的时候,最少也是二阶驻点,这已经算是高阶驻点了。理论上说,高阶驻点在做梯度下降法的时候是很难脱离的。
拿上面的海森矩阵为例,就看第一个的情况,对于
来说,
和
都是从第一个residual unit里面随机选的,那么,就只有当
和
分处在不同的
的时候,才会有
。换言之,只有下图中橙色和蓝色的块块才能有非零值的存在(只考虑第一个residual unit)。
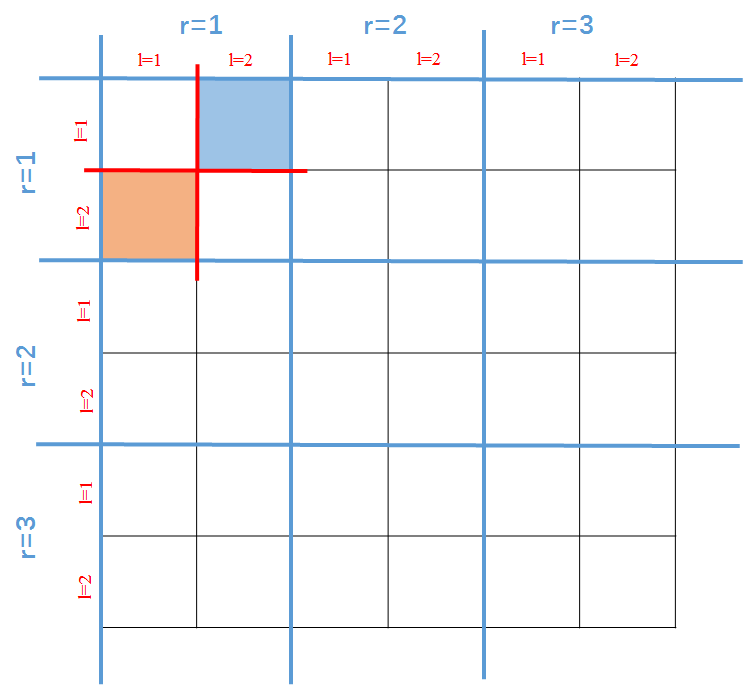
延展到全部的海森矩阵就有下面这些非零的存在。
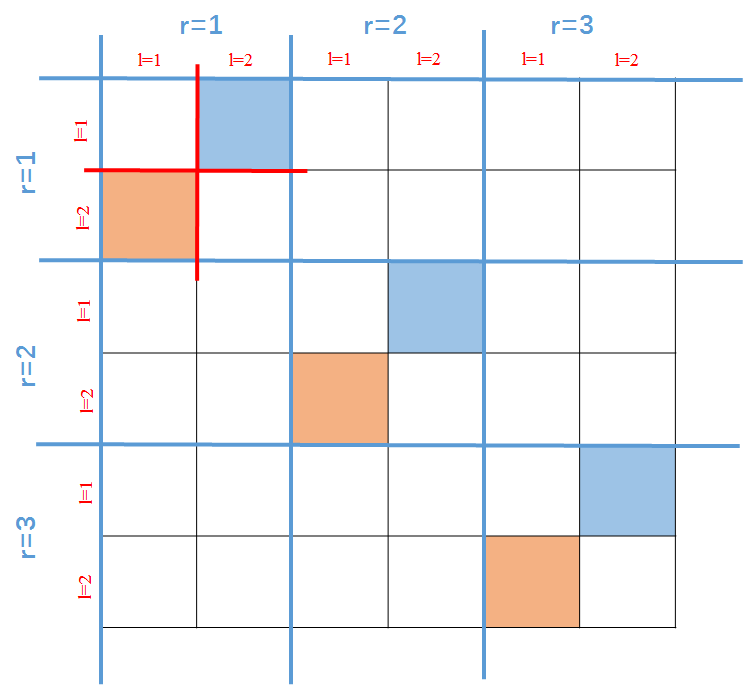
引入定理2:
对于两个在不同residual unit里的权重
,并且有
,定义损失函数
是将
都置0的损失函数。于是
就等于任意满足同样r关系的任意
的
。
这个定理初听很拗口,把它分情况讨论一下
,此时可以保证下图中,0初始化时,所有A都是相等的,所有B都是相等的,所有C都是相等的,所有D都是相等的;当然因为由定理1知道除了A,B其余全部都是0,所以所有B和C都是各自相等且不为零。
,此时考虑的就是我们的微分顺序了。实际上
如果成立,那么必然有下图中的 E 全部相等,又由定理 1 知道,其值全部为 0。同理,如果
,那么下图中所有 F 全部相等,并且为 0。
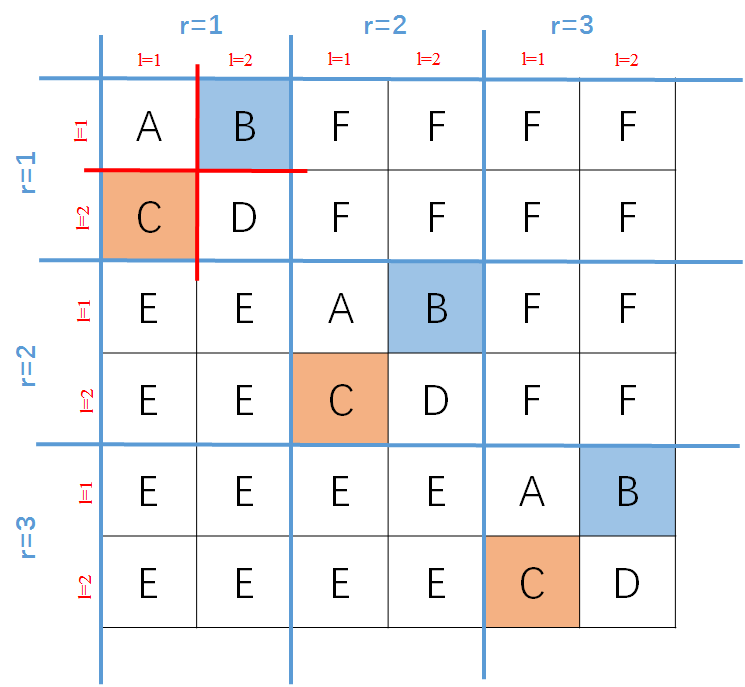
2-shortcuts
综上,我们知道,在2-shortcuts的情况下,根据海森矩阵的对称性,我们得到海森矩阵为
根据分块矩阵的特性,可以知道这个海森矩阵的特征值可以表示为
%0A%3D%5Ctext%7Beigs%7D(h)%0A%3D%5Cpm%20%5Ctext%7Beigs%7D(A%5ETA)%0A%0Ah%3D%5Cbegin%7Bbmatrix%7D%20%0A%5Cmathbf%7B0%7D%26A%5ET%5C%5C%0AA%26%5Cmathbf%7B0%7D%0A%5Cend%7Bbmatrix%7D#card=math&code=%5Ctext%7Beigs%7D%28H%29%0A%3D%5Ctext%7Beigs%7D%28h%29%0A%3D%5Cpm%20%5Ctext%7Beigs%7D%28A%5ETA%29%0A%0Ah%3D%5Cbegin%7Bbmatrix%7D%20%0A%5Cmathbf%7B0%7D%26A%5ET%5C%5C%0AA%26%5Cmathbf%7B0%7D%0A%5Cend%7Bbmatrix%7D&id=dcfd5db6)
所以根据条件数的定义
所以最终其条件数就可以写成
%3D%5Csqrt%7B%5Ctext%7Bcond%7D(A%5ETA)%7D#card=math&code=%5Ctext%7Bcond%7D%28H%29%3D%5Csqrt%7B%5Ctext%7Bcond%7D%28A%5ETA%29%7D&id=54c801f5)
下面考虑A的形式了,看它到底和深度有没有关系。
首先对于权重矩阵中的某一个权重,其坐标大概是这样的
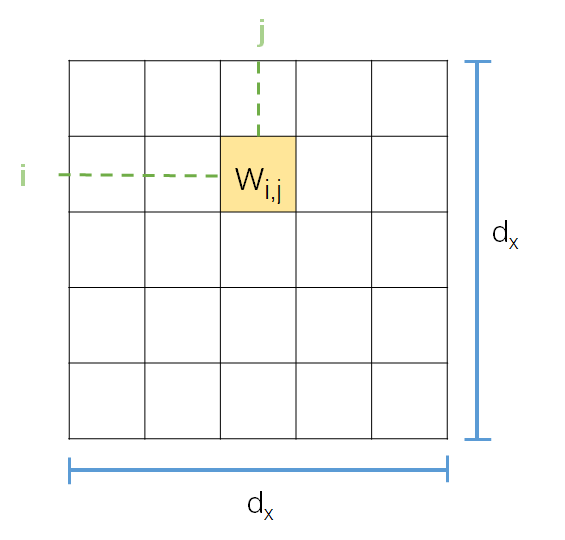
将其拉成一行,其index则变为了 或者
都可以。但是在本文中,是按照前者来的,这一点需要注意。
假设有两个参数,假设我们的
矩阵就是在
上的两个权重矩阵。
那么假设是 的权重矩阵,那么A的造型大概是这样的
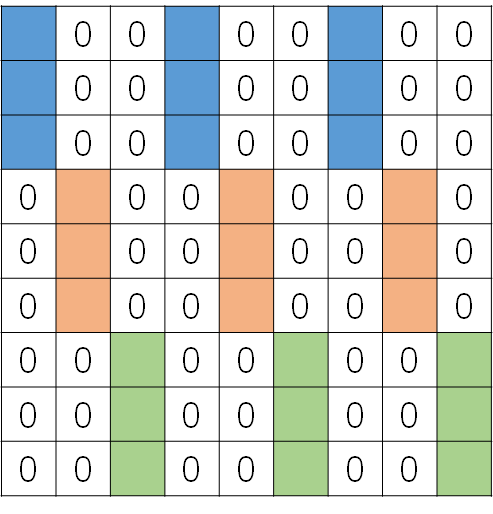
注意,我们是按列展开的。
当 的时候(代表了两个参数连接到了同一个神经元,每一个
在海森矩阵中代表9个参数),我们可以得到
dx%2Bi_1%2C(j_2-1)d_x%2Bi_2%7D%0A%0A%3D%5Cfrac%7B%5Cpartial%5E2%5Csum%5Em%7B%5Cmu%3D1%7D%5Cfrac%7B1%7D%7B2m%7D(y%7Bi_1%7D%5E%7B%5Cmu%7D-x%7Bi1%7D%5E%7B%5Cmu%7D-w_1w_2x%7Bj2%7D%5E%7B%5Cmu%7D)%5E2%7D%7B%5Cpartial%7Bw_1%7D%5Cpartial%7Bw_2%7D%7D%5Cbigg%7C%7B%5Cmathbf%7Bw%7D%3D0%7D%0A%0A%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%7B%5Cmu%3D1%7D%5Em%7Bx%7Bj2%7D%5E%7B%5Cmu%7D(x%7Bi1%7D%5E%7B%5Cmu%7D-y%7Bi1%7D%5E%7B%5Cmu%7D)%7D%0A%0A%3D%5CSigma%5E%7BXX%7D-%5CSigma%5E%7BYX%7D#card=math&code=A%7B%28j1-1%29d_x%2Bi_1%2C%28j_2-1%29d_x%2Bi_2%7D%0A%0A%3D%5Cfrac%7B%5Cpartial%5E2%5Csum%5Em%7B%5Cmu%3D1%7D%5Cfrac%7B1%7D%7B2m%7D%28y%7Bi_1%7D%5E%7B%5Cmu%7D-x%7Bi1%7D%5E%7B%5Cmu%7D-w_1w_2x%7Bj2%7D%5E%7B%5Cmu%7D%29%5E2%7D%7B%5Cpartial%7Bw_1%7D%5Cpartial%7Bw_2%7D%7D%5Cbigg%7C%7B%5Cmathbf%7Bw%7D%3D0%7D%0A%0A%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%7B%5Cmu%3D1%7D%5Em%7Bx%7Bj2%7D%5E%7B%5Cmu%7D%28x%7Bi1%7D%5E%7B%5Cmu%7D-y%7Bi_1%7D%5E%7B%5Cmu%7D%29%7D%0A%0A%3D%5CSigma%5E%7BXX%7D-%5CSigma%5E%7BYX%7D&id=7a4b074a)
其中,关于如何从 推得
稍微有些麻烦。以下推导可以跳过,不影响阅读。
推导过程:
我们知道
并且,我们有
#card=math&code=W%3D%5Cprod%7Br%3D1%7D%5ER%28%5Cprod%5En%7Bl%3D1%7DW%5E%7Br%2Cl%7D%2BI_%7Bd_x%7D%29&id=b5634b4b)
现在我们知道选取的两个参数分别属于同一个residual unit里面相邻的两个权重矩阵。
于是,我们可以将 写成如下形式
)%5D(W%5E%7Br%2C2%7D%2BI%7Bd_x%7D)(W%5E%7Br%2C1%7D%2BI%7Bdx%7D)%5B%5Cprod%7Br0%3Dr%2B1%7D%5E%7BR%7D(%5Cprod%5En%7Bl%3D1%7DW%5E%7Br%2Cl%7D%2BI%7Bd_x%7D)%5D%0A%0A%3DM(W%5E%7Br%2C2%7D%2BI%7Bdx%7D)(W%5E%7Br%2C1%7D%2BI%7Bdx%7D)N#card=math&code=W%3D%5B%5Cprod%7Br0%3D1%7D%5E%7Br-1%7D%28%5Cprod%5En%7Bl%3D1%7D%28W%5E%7Br0%2Cl%7D%2BI%7Bdx%7D%29%29%5D%28W%5E%7Br%2C2%7D%2BI%7Bdx%7D%29%28W%5E%7Br%2C1%7D%2BI%7Bdx%7D%29%5B%5Cprod%7Br0%3Dr%2B1%7D%5E%7BR%7D%28%5Cprod%5En%7Bl%3D1%7DW%5E%7Br%2Cl%7D%2BI%7Bd_x%7D%29%5D%0A%0A%3DM%28W%5E%7Br%2C2%7D%2BI%7Bdx%7D%29%28W%5E%7Br%2C1%7D%2BI%7Bd_x%7D%29N&id=119f3664)
于是我们将 中的
单独取出来,可以得到
(W%5E%7Br%2C1%7D%2BI%7Bd_x%7D)Nx%5E%7B%5Cmu%7D#card=math&code=y%5E%7B%5Cmu%7D-Wx%5E%7B%5Cmu%7D%3Dy%5E%7B%5Cmu%7D-M%28W%5E%7Br%2C2%7D%2BI%7Bdx%7D%29%28W%5E%7Br%2C1%7D%2BI%7Bd_x%7D%29Nx%5E%7B%5Cmu%7D&id=c0dd14c0)
当取 的时候,我们可以知道,该等式变为
,但是,对于求取关于
的偏导,我们就可以先将其余不包含
的部分变为单位矩阵,即
(W%5E%7Br%2C1%7D%2BI%7Bd_x%7D)x%5E%7B%5Cmu%7D%0A%0A%3Dy%5E%7B%5Cmu%7D-(W%5E%7Br%2C2%7DW%5E%7Br%2C1%7D%2BW%5E%7Br%2C1%7D%2BW%5E%7Br%2C2%7D%2BI%7Bdx%7D)x%5E%7B%5Cmu%7D%0A%0A%3Dy%5E%7B%5Cmu%7D-x%5E%7B%5Cmu%7D-(W%5E%7Br%2C2%7DW%5E%7Br%2C1%7D%2BW%5E%7Br%2C1%7D%2BW%5E%7Br%2C2%7D)x%5E%7B%5Cmu%7D#card=math&code=y%5E%7B%5Cmu%7D-%28W%5E%7Br%2C2%7D%2BI%7Bdx%7D%29%28W%5E%7Br%2C1%7D%2BI%7Bdx%7D%29x%5E%7B%5Cmu%7D%0A%0A%3Dy%5E%7B%5Cmu%7D-%28W%5E%7Br%2C2%7DW%5E%7Br%2C1%7D%2BW%5E%7Br%2C1%7D%2BW%5E%7Br%2C2%7D%2BI%7Bd_x%7D%29x%5E%7B%5Cmu%7D%0A%0A%3Dy%5E%7B%5Cmu%7D-x%5E%7B%5Cmu%7D-%28W%5E%7Br%2C2%7DW%5E%7Br%2C1%7D%2BW%5E%7Br%2C1%7D%2BW%5E%7Br%2C2%7D%29x%5E%7B%5Cmu%7D&id=5b1ba5f8)
当的时候,我们有参数
连接到同一个神经元上。此时,必然只有和
对于
的偏导不为0。意即,我们对于上式,将只能考虑和
相连的神经元。
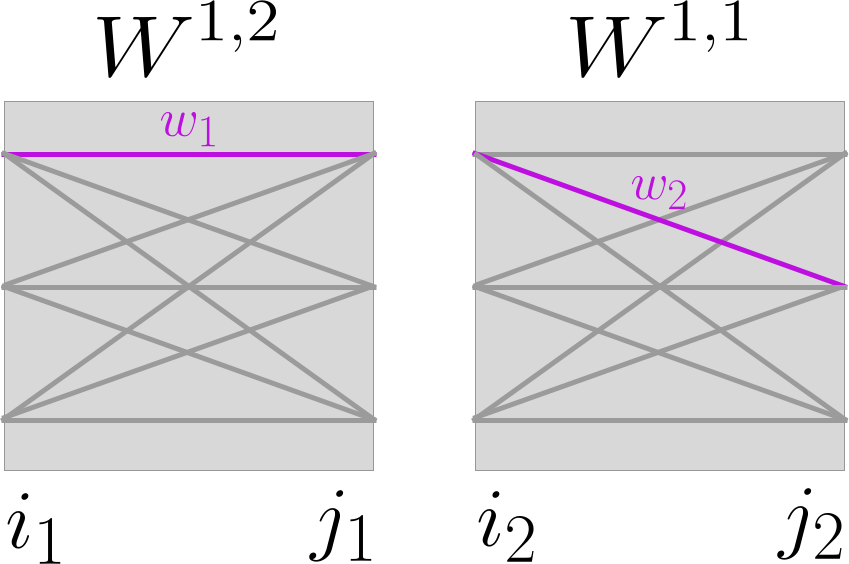
将其变化为
关于这个式子,有以下解释:
代表了shortcut的连接,经过了两个权重矩阵,仍然是
还是
。
- 后面的
,是由
演化而来。
x%5E%7B%5Cmu%7D%0A%0A%3DW%5E%7Br%2C1%7DW%5E%7Br%2C2%7Dx%5E%7B%5Cmu%7D%2BW%5E%7Br%2C1%7Dx%5E%7B%5Cmu%7D%2BW%5E%7Br%2C2%7Dx%5E%7B%5Cmu%7D%0A%0A%3Dw1w_2x%7Bj2%7D%5E%7B%5Cmu%7D-w_1x%7Bj2%7D%5E%7B%5Cmu%7D-w_2x%7Bj2%7D%5E%7B%5Cmu%7D%0A%0A%3Dw_1w_2x%7Bj2%7D%5E%7B%5Cmu%7D#card=math&code=%28W%5E%7Br%2C1%7DW%5E%7Br%2C2%7D%2BW%5E%7Br%2C1%7D%2BW%5E%7Br%2C2%7D%29x%5E%7B%5Cmu%7D%0A%0A%3DW%5E%7Br%2C1%7DW%5E%7Br%2C2%7Dx%5E%7B%5Cmu%7D%2BW%5E%7Br%2C1%7Dx%5E%7B%5Cmu%7D%2BW%5E%7Br%2C2%7Dx%5E%7B%5Cmu%7D%0A%0A%3Dw_1w_2x%7Bj2%7D%5E%7B%5Cmu%7D-w_1x%7Bj2%7D%5E%7B%5Cmu%7D-w_2x%7Bj2%7D%5E%7B%5Cmu%7D%0A%0A%3Dw_1w_2x%7Bj_2%7D%5E%7B%5Cmu%7D&id=fe276102)
单独的和
显然为 0,在求取
偏导,且
的情况下。
综上,得证。
否则, 的元素为0。于是,我们就可以得到上面的那个图。其中,蓝色为
,红色为
,绿色为
。
这个矩阵的特征值怎么求啊,别慌,我们需要借助置换矩阵。什么是置换矩阵?简言之,就是每行每列有且只有一个元素为1,其余都是0的矩阵。
这个置换矩阵是这样定义的,对于置换矩阵 ,其元素
不为0,当且仅当
,以9x9为例,
可以表示为
因此,A可以表示为
注意这里的全是3x3的矩阵
所以,矩阵
置换矩阵有个性质,,根据相似矩阵的特性:特征值相等,可以得到
%3D%5Cpm%5Ctext%7Beigs%7D(A%5ETA)%3D%5Cpm%5Csqrt%7B%5Ctext%7Beigs%7D(%5CSigma%5E%7BXX%7D-%5CSigma%5E%7BYX%7D)%5ET(%5CSigma%5E%7BXX%7D-%5CSigma%5E%7BYX%7D)%7D#card=math&code=%5Ctext%7Beigs%7D%28H%29%3D%5Cpm%5Ctext%7Beigs%7D%28A%5ETA%29%3D%5Cpm%5Csqrt%7B%5Ctext%7Beigs%7D%28%5CSigma%5E%7BXX%7D-%5CSigma%5E%7BYX%7D%29%5ET%28%5CSigma%5E%7BXX%7D-%5CSigma%5E%7BYX%7D%29%7D&id=898f214e)
显然这是一个深度无关的值,可以预见,其海森矩阵的条件数在初始化的时候是一个常数,从而使得无论是深层的还是浅层的ResNet,其初始的训练难度是一样的。
1-shortcut
分析完了2-shortcuts和3+-shortcuts的情况,我们还有最后一个情况,1-shortcut。
1-shortcut 不存在同一个residual unit里面包含2个或以上的权重矩阵,里面只包含1个。在这种情况下,对于上述的定理1和定理2,可以做不同的解读。
首先是定理1,我们我们已经不存在可以满足定理1的子矩阵了,因此,海森矩阵所有的包含的子矩阵全部为非零。
其次是定理2,
时,即对角线上矩阵,只能保证对角线上全部相等,记为
时对角线下方全部一样(记为
),根据海森矩阵对称性,上半部分全是下半部分的矩阵(记为
)
综上,可以知道海森矩阵可以写成
下面来讨论关于 的表达式。
对于 来说,现假设存在两个参数
,注意到它们的residual unit是一样的,所在权重矩阵也是一样的。那么,我们可以得到
dx%2Bi_1%2C(j_2-1)d_x%2Bi_2%7D%3D%5Cbegin%7Bcases%7D%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7Dx%7Bj_1%7D%5E%7B%5Cmu%7Dx%7Bj2%7D%5E%7B%5Cmu%7D%26%20i_1%3Di_2%5C%5C%0A0%26%20i_1%5Cne%20i_2%0A%5Cend%7Bcases%7D#card=math&code=B%7B%28j1-1%29d_x%2Bi_1%2C%28j_2-1%29d_x%2Bi_2%7D%3D%5Cbegin%7Bcases%7D%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7Dx%7Bj_1%7D%5E%7B%5Cmu%7Dx%7Bj_2%7D%5E%7B%5Cmu%7D%26%20i_1%3Di_2%5C%5C%0A0%26%20i_1%5Cne%20i_2%0A%5Cend%7Bcases%7D&id=e20f44d4)
其大概是这也的造型

关于 如何得到的,可选择性看下方推导。
推导过程:
因为针对的是1-shortcut,所有操作在一个residual unit里面进行,所以必须考虑到其自乘的特点。
首先先得到的是
x%5E%7B%5Cmu%7D)%5E2%0A%0A%3D%20(y%5E%7B%5Cmu%7D)%5E2-2(W%5E%7Br%2C1%7D%2BI%7Bd_x%7D)x%5E%7B%5Cmu%7D%2B((W%5E%7Br%2C1%7D%2BI%7Bdx%7D)%5E2x%5E%7B%5Cmu%7D)%5E2%7C%7B%5Cmathbf%7Bw%7D%3D0%7D%0A%0A%3D(W%5E%7Br%2C1%7D)%5ETW%5E%7Br%2C1%7D(x%5E%7B%5Cmu%7D)%5E2%0A%0A%3Dw1w_2x%5E%7B%5Cmu%7D%7Bj1%7Dx%5E%7B%5Cmu%7D%7Bj2%7D#card=math&code=%28y%5E%7B%5Cmu%7D-%28W%5E%7Br%2C1%7D%2BI%7Bdx%7D%29x%5E%7B%5Cmu%7D%29%5E2%0A%0A%3D%20%28y%5E%7B%5Cmu%7D%29%5E2-2%28W%5E%7Br%2C1%7D%2BI%7Bdx%7D%29x%5E%7B%5Cmu%7D%2B%28%28W%5E%7Br%2C1%7D%2BI%7Bdx%7D%29%5E2x%5E%7B%5Cmu%7D%29%5E2%7C%7B%5Cmathbf%7Bw%7D%3D0%7D%0A%0A%3D%28W%5E%7Br%2C1%7D%29%5ETW%5E%7Br%2C1%7D%28x%5E%7B%5Cmu%7D%29%5E2%0A%0A%3Dw1w_2x%5E%7B%5Cmu%7D%7Bj1%7Dx%5E%7B%5Cmu%7D%7Bj_2%7D&id=f5540097)
综上,得证。
同样使用置换矩阵,可以得到
如果说 代表的是同一个residual unit,那么
代表的就是不同的residual unit之间的运算,假设有两个参数
,且
。那么对于A来说:
dx%2Bi_1%2C(j_2-1)d_x%2Bi_2%7D%3D%5Cfrac%7B%5Cpartial%5E2L%7D%7B%5Cpartial%7Bw_1%7D%5Cpartial%7Bw_2%7D%7D%5CBig%7C%7B%5Cmathbf%7Bw%7D%3D0%7D%0A%0A%3D%5Cbegin%7Bcases%7D%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7D(x%7Bi1%7D%5E%7B%5Cmu%7D-y%7Bi1%7D%5E%7B%5Cmu%7D)x%7Bj1%7D%5E%7B%5Cmu%7D%2Bx%7Bj1%7D%5E%7B%5Cmu%7Dx%7Bj2%7D%5E%7B%5Cmu%7D%26j_1%3Di_2%2Ci_1%3Di_2%5C%5C%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7D(x%7Bi_1%7D%5E%7B%5Cmu%7D-y%7Bi1%7D%5E%7B%5Cmu%7D)x%7Bj1%7D%5E%7B%5Cmu%7D%26j_1%3Di_2%2Ci_1%5Cne%20i_2%5C%5C%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7Dx%7Bj_1%7D%5E%7B%5Cmu%7Dx%7Bj2%7D%5E%7B%5Cmu%7D%26j_1%5Cne%20i_2%2Ci_1%3Di_2%5C%5C%0A0%26j_1%5Cne%20i_2%2Ci_1%5Cne%20i_2%0A%5Cend%7Bcases%7D#card=math&code=A%7B%28j1-1%29d_x%2Bi_1%2C%28j_2-1%29d_x%2Bi_2%7D%3D%5Cfrac%7B%5Cpartial%5E2L%7D%7B%5Cpartial%7Bw_1%7D%5Cpartial%7Bw_2%7D%7D%5CBig%7C%7B%5Cmathbf%7Bw%7D%3D0%7D%0A%0A%3D%5Cbegin%7Bcases%7D%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7D%28x%7Bi1%7D%5E%7B%5Cmu%7D-y%7Bi1%7D%5E%7B%5Cmu%7D%29x%7Bj1%7D%5E%7B%5Cmu%7D%2Bx%7Bj1%7D%5E%7B%5Cmu%7Dx%7Bj2%7D%5E%7B%5Cmu%7D%26j_1%3Di_2%2Ci_1%3Di_2%5C%5C%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7D%28x%7Bi_1%7D%5E%7B%5Cmu%7D-y%7Bi1%7D%5E%7B%5Cmu%7D%29x%7Bj1%7D%5E%7B%5Cmu%7D%26j_1%3Di_2%2Ci_1%5Cne%20i_2%5C%5C%0A%5Cfrac%7B1%7D%7Bm%7D%5Csum%5Em%7B%5Cmu%3D1%7Dx%7Bj_1%7D%5E%7B%5Cmu%7Dx%7Bj_2%7D%5E%7B%5Cmu%7D%26j_1%5Cne%20i_2%2Ci_1%3Di_2%5C%5C%0A0%26j_1%5Cne%20i_2%2Ci_1%5Cne%20i_2%0A%5Cend%7Bcases%7D&id=776aba47)
总共有2种情况:
,此种情况下,两个residual unit首尾相连,要求偏导的两个参数连接到同一个神经元上面(同2-shortcut情况)
,此种情况下,两个参数输出的神经元的编号相同(和B相同)
则可以推得上述式子。
也就可以得到$A$的表达式:
显然,此时海森矩阵 是一个Toeplitz矩阵,当网络深度增加的时候,其规模也越大。根据Toeplitz矩阵的性质,我们知道其条件数随着矩阵规模增大而增大,永无止境。可以参考[2]。
由此,得出所有的0初始化时的情况:
- 2+-shortcuts:海森矩阵为0矩阵,且其为高阶驻点,难以逃脱0初始化的情况
- 2-shortcuts:条件数为常数,表现为深度无关
- 1-shortcut:条件数随着深度增加而增加,这为收敛带来了很大难度。
实验结果
我们总共比较3种情况(1-shortcut和第二种类似,在此省略)
- 线性网络-Xavier初始化
- 线性网络-Orthogonal初始化
- 2-shortcuts线性网络-0初始化
效果如下
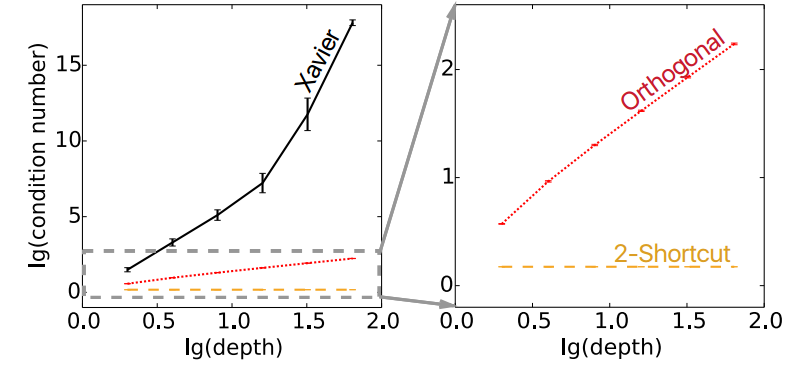
很显然,当2-shortcuts线性网络-0初始化的时候,我们得到的条件数是一个常数,且处于相对较低的位置。
学习过程
初始化好,不代表这个网络就好,我们还要看过程和结果。研究过程中的条件数的变化是研究的目的。
首先,想要求出这样的一个结果,我们就要关注海森矩阵的特征值。在实际实验过程中,很难取得其最小值(不稳定),我们取10%的海森矩阵特征值。
实验结果如下:
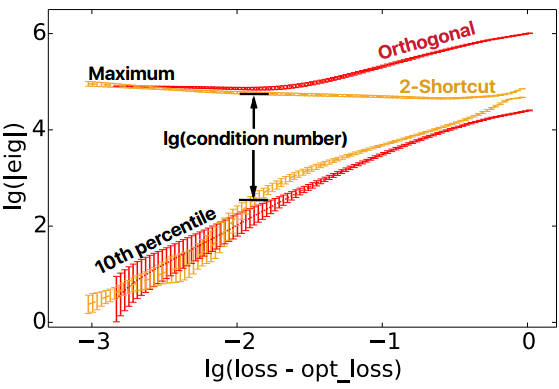
结论是这样的,随着loss越来越接近optimal loss:
- orthogonal和2-shortcut条件数都很小,而且一定程度上相似
- 越到后面2-shortcuut条件数越小,意味着优化越容易
另一个实验观察了负特征值的比率,这是一个非常有用的特性,是临界点的重要特征。这里有两个要注意
- 观察负特征值到底有什么用
- 和临界点有什么关系
loss越大,负特征值比率越大
结果
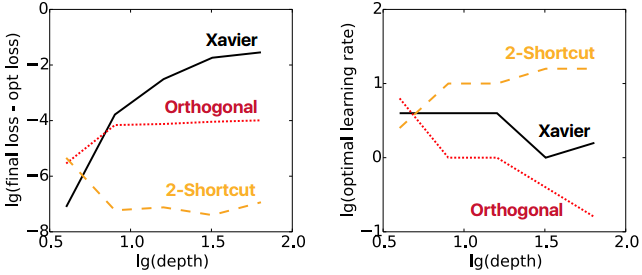
负特征值在开始有一个骤降,作者给出的解释是初始点靠近鞍点,导致其在初始的时候就向负曲率方向移动,这消除了部分负特征值。同时在右图中,可以看出index骤降达到最小值的时候,梯度也骤升达到最大值
训练结果
开始和过程都考虑了,那么最终结果如何?对Xavier线性,Orthogonal线性,2-shortcut线性分别做1000 epoch训练,比较其最终结果和学习率
结果如下
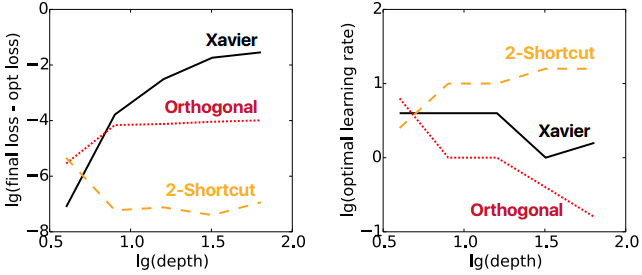
可见,2-shortcut的1000次最终结果都和最优的相差不大,同时可以获得较高的学习率。
我们之前研究过,大于两层hidden的线性网络就会具有非线性的特征,那么我们加入非线性激活函数来验证下和上面的线性是否一致。
显然,类似。