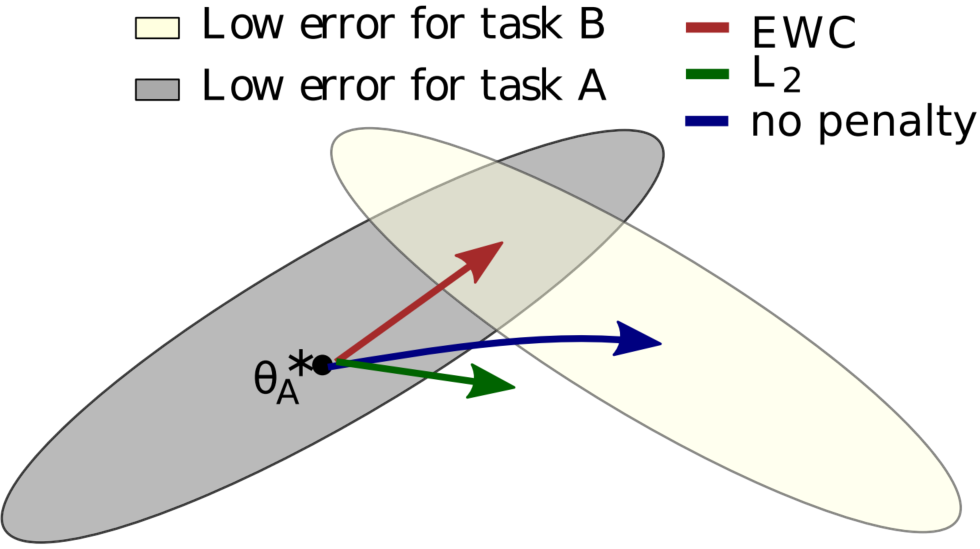
在连续学习的正则化方法中，构建Importance Matrix的方法有很大的影响力。其原理是对参数有关老任务部分进行约束更新。根据方法出现前后顺序，主要存在以下几种方法。

EWC

Kirkpatrick J, Pascanu R, Rabinowitz N, et al. Overcoming catastrophic forgetting in neural networks[J]. Proceedings of the national academy of sciences, 2017, 114(13): 3521-3526.

EWC 作为该类开创方法之一，从小鼠突触通过学习某类知识之后会一直保留的现象，提出Task-specific Synaptic Consolidation的解决方案。出发点是当前的神经网络过参数化严重，让模型中的个部分参数对应不同任务是可以满足的。

参数约束通过二次约束Quadratic Penalty实现，难点在于寻找哪些参数是对哪些任务重要。

Quadratic Penalty

监督学习模型的学习过程可以认为是求的过程，根据贝叶斯公式可以得到

其中，可以由损失函数的相反数得到，即。

假设 ，由两个独立的数据集构成，那么上式可以化为

在连续学习中，如果是先学习任务A再学习任务B，可以认为可以认为是之前任务学习的后验概率，是已知的。

为了衡量哪些参数对任务 A 重要，利用拉普拉斯近似，将该重要性的后验近似为一个高斯分布，均值为上一个任务学得的参数 ，对角精度由费雪矩阵 给定。

费雪矩阵的关键特性：

• 等价于loss的二阶导的局部最小值
• 容易计算，从一阶导求得
• 是半正定的

EWC的损失函数可以定义为

EWC 采用 Fisher 矩阵近似参数的二阶导（海森矩阵）。

解析

根据最大化后验概率的目的，上式 可以化为目标函数：

其中，即参数对数据的条件概率，表现为损失的值，即最大化后验概率等价于，最小化损失函数；则可以看作是任务A训练好的参数。

连续学习在训练任务B的时候，认为是不可见的，因此，无法在训练的时候直接获得后验。常用的近似方法如变分推断、MCMC、拉普拉斯（Laplace）近似之类的，论文用了拉普拉斯近似。

拉普拉斯近似

拉普拉斯近似采用一个高斯分布来近似。假设 ，那么有

上式中， 是参数变量， 是不可见的，如何让 的更新受到该高斯分布的约束。显然，对于任务A， 的期望是 ，在 处展开：

因为 时 取最大值，可以认为其一阶导雅各比矩阵为0。又因为概率密度函数在一维空间上，因此有

代表了海森矩阵，在EWC中代表了重要性矩阵Importance Matrix， 根据约等式可以推得

那么上述优化问题可以化为

能直接算出来，但是这里参数 是 维向量，所以是 的海森矩阵，计算的时间和空间复杂度都比较大。为了减小计算开销，论文把海森矩阵转成了 Fisher 信息矩阵。

Fisher 信息矩阵

Fisher 信息矩阵等于海森矩阵的期望取负（这里是证明过程）：

费雪信息矩阵只需要计算一阶导 (Fisher 定义)，计算量很低。假设各参数之间相互独立，可以只取费雪矩阵的对角线，即

采用蒙特卡洛采样，从数据集中采样来计算Fisher矩阵

在任务A上训练完成之后获得 ，在此基础上重新采样所有数据，得每个样本的梯度平方的期望，就可以得到Fisher 信息矩阵（对角）。

所以，最终的EWC的训练损失函数是

Fisher 信息矩阵也反映了我们对参数估计的不确定度。二阶导越大，说明我们对该参数的估计越确定，同时 Fisher 信息也越大，惩罚项就越大。于是越确定的参数在后面的任务里更新幅度就越小。

EWC针对每个任务都构建一个Fisher矩阵和对应惩罚项，随着任务数目增多，性能会比较大的降低。

MAS

SI

SSR