贝叶斯平滑要解决的问题：商品的历史点击率不能代表真实情况。
例如：
- 历史中商品只出现一次，且被点击了，并不能代表它的点击率就是1.
- 历史中商品没有出现，也不能代表点击率为0。
贝叶斯平滑理论
贝叶斯平滑的核心思想是：假设商品的点击率不仅与观测到的点击率，还与隐含的点击率有关；且假设观测到的点击率服从伯努利分布，隐含的点击率服从Beta分布。其中，Binomail分布和Beta分布互为共轭分布，因此若Binomail分为似然函数，Beta分布为先验分布，则后验分布仍然为Beta分布。如下图1所示，贝叶斯平滑的概率图。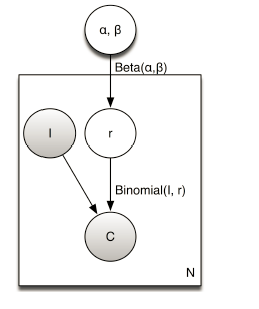
图1 贝叶斯平滑概率图
公式推导
(1)
对其取log，且求导可得
(2)
(3)
令求导后的结果为0，即可得到最优的
和
。
贝叶斯平滑后的点击率，如下公式(4)所示。
(4)
参数估计
后验Beta分布的参数估计可以采取矩估计和Fixed-point iteration。
矩估计
对于Beta分布的矩估计是根据均值和方差进行参数估计，如下式(5)和(6)所示，参数的估计公式。
(5)
(6)
Fixed-point iteration
该方式对参数进行估计的步骤如下:
- 首先给出参数的初始值。
- 在初始值处，构造一个似然函数的下界函数。求得该下届函数的最大值的闭式解，带入到下次迭代。
- 不断重复上述1,2步骤，直至收敛。
该方式类似于EM算法的核心思想。
参考文献
若有收获，就点个赞吧
0 人点赞
