简介
遗传算法(Genetic Algorithm,GA)的算法思想来源于达尔文的进化论学说和Mendel的遗传理论,本质是模拟种群个体不断进化以逐渐适应环境的过程。遗传算法通过自然选择、交叉、变异等遗传操作模拟种群进化过程,使种群中个体的优良基因得以保留,提高个体的适应能力,进而不断增强对环境的适应能力。
遗传算法是以染色体形式对问题的解进行描述,首先需要对问题的解进行编码,编码方式可以使用实数编码、二进制编码、符号编码。
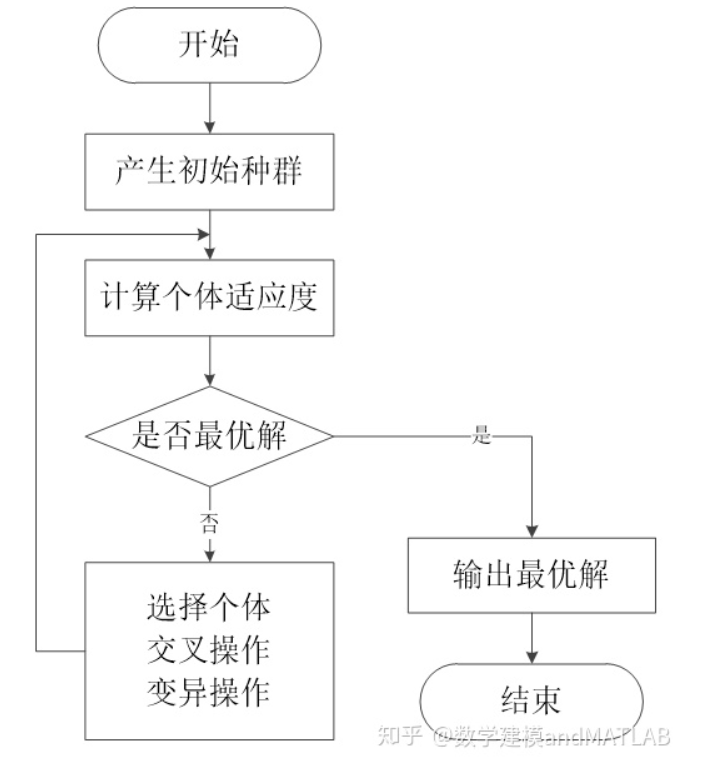
在算法初始化时,首先随机产生一批初始种群,根据适应度函数公式计算种群中各个染色体的适应度值;进一步,按照适者生存、优胜劣汰的法则,选择种群中的个体进行复制、交叉、变异的遗传操作产生出子代染色体,个体适应度越大被选择进行遗传操作的概率越高,从而将种群中的优良基因进行保留同时适应度较差的个体将逐渐被淘汰;最后,进化多代后达到算法终止条件,算法收敛到某个对环境适应性最好的染色体上,这个染色体对应的编码也就是该问题的最优解。遗传算法的算法流程如图所示。
样例
我们以麦当劳积分兑换商品为例,详细介绍一下遗传算法的原理。
假设我们现在有900的麦当劳积分,可以兑换下面这8种商品,每种商品对应售价不同,需要不同的积分,我们希望可以用900积分兑换尽可能贵的商品,该如何兑换呢?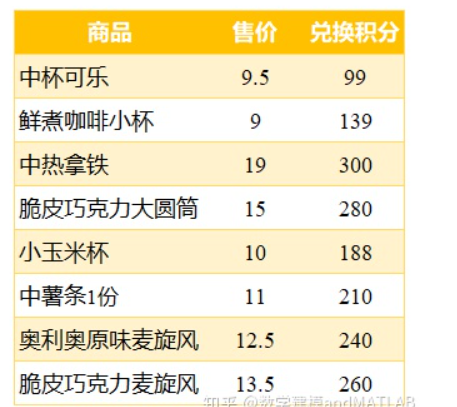
由问题背景可知,该问题的适应度函数为商品总售价,总售价越大越好。
问题转化:设麦当劳积分兑换活动有N个商品,第个商品的价值为vi元,兑换需要wi个积分,每个商品仅能兑换一次。我们总共有W个积分,我们希望用积分兑换的东西越值钱越好,到底应该怎么兑换呢?设xi表示第i件商品的兑换状态,1代表兑换,0代表不兑换,搜索空间为n元一维数组(×1,×2,x3..….xn)。因而解空间的取值范围可表示为(0,0,0,…,0),(0,0,0,..….1),(0,0,0,.….1,0),.….(1,1,1,1.….1)。
以3个商品为例,解(0,1,0)表示(不兑换商品0,兑换商品1,不兑换商品2)。
目标函数:积分兑换的商品总价值z最大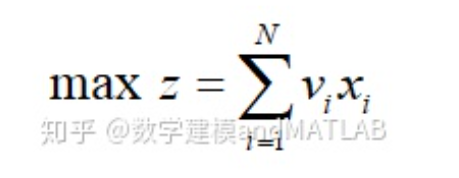
约束条件:兑换商品所用的积分不大于拥有的总积分W;每个商品有兑换和不兑换两种状态,
兑换: xi=1
不兑换:xi=0
数学模型: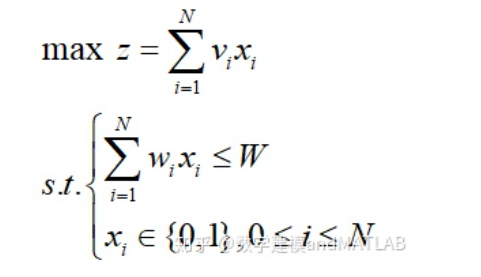
第一步:编码、产生初始种群,计算适应度函数
随机生成初始种群,种群中包含8个个体,每个个体上有8个基因位点,只有0或1两种取值,分别表示是否兑换该商品,进而可以计算出对应的适应度函数,也就是兑换商品的总价值,以及所需积分是否超过阈值,这里取积分最大不超过900,若所需积分超过900,则兑换不成功,适应度函数取值为0。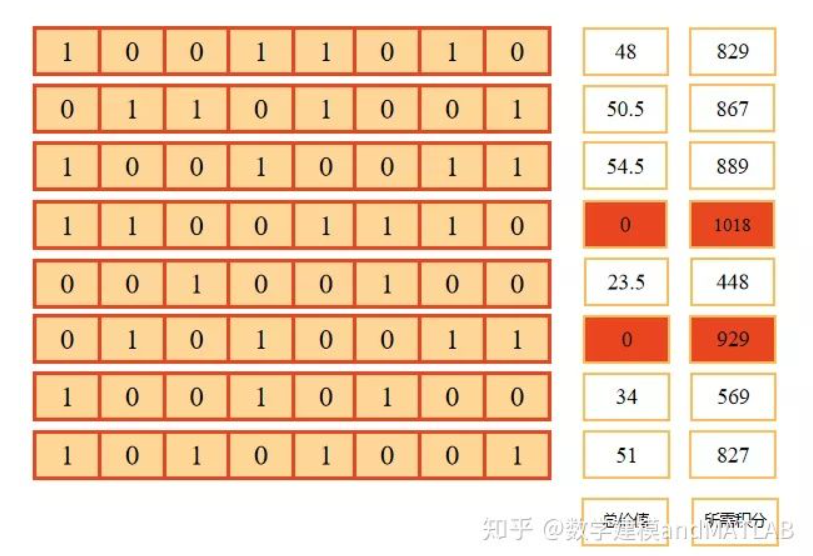
第二步:选择适应度最大的个体,进入下一代,个体被选中的概率可表示为
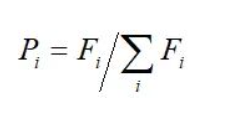
计算累积概率,判断随机数落在哪个区间上,选择该个体进入下一代,重复8次,选择8个个体组成下一代新种群。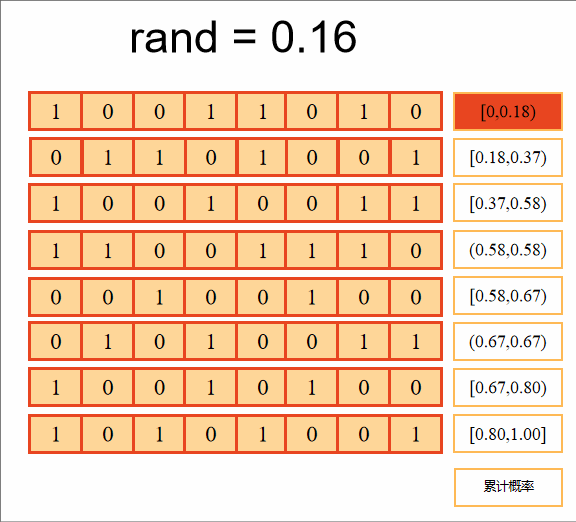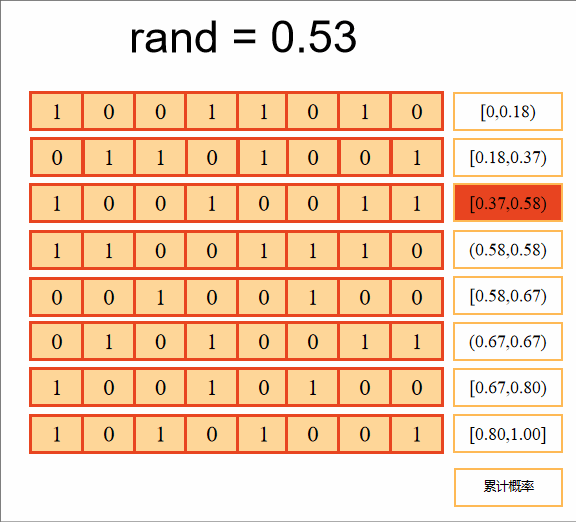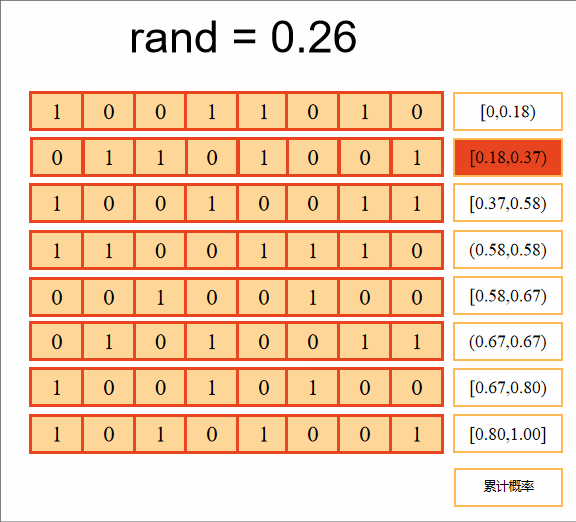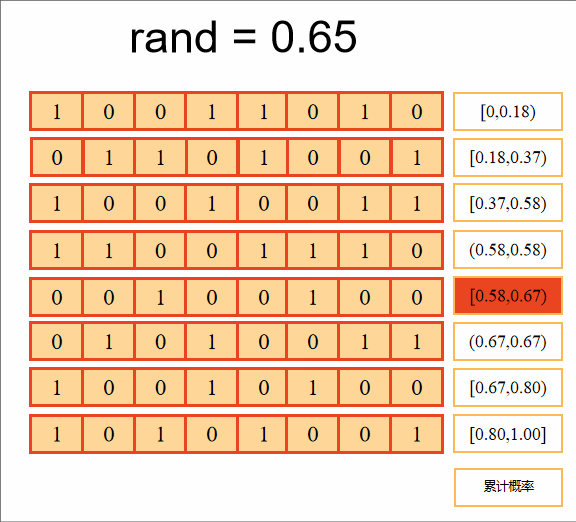
第三步:交叉变异,两两个体匹配,进行交叉判断,判断随机数是否小于交叉概率,如果是则进行交叉,否则不进行交叉,这里取交叉概率为0.7;

染色体交叉过程中,随机选了一段基因序列,将两个体中对应序列交换
[
](https://pic4.zhimg.com/50/v2-e3cc378107ce612279032c535ac4f0a6_hd.webp?source=1940ef5c)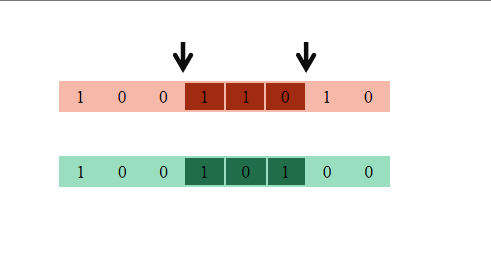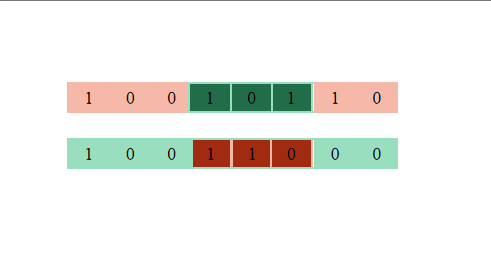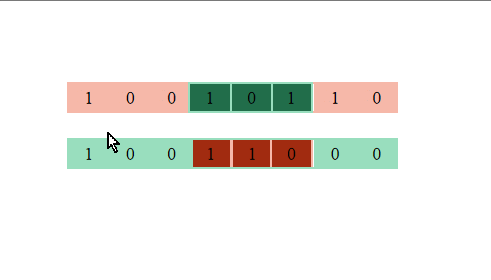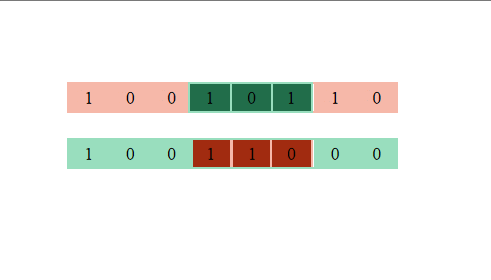
第四步:基因突变,在每个个体的每个基因位点进行判断,判断随机数是否小于突变概率(这里取0.1),如果是则原基因位点取值进行翻转,否则取值不变。

以上,即完成了一代进化,判断是否达到最大进化次数,如果是,输出当前最优解,否则,返回第一步,继续进化。按照上述过程中,我们在matlab中进行求解积分兑换问题,在进行100次进化之后,其适应度函数变化趋势为:
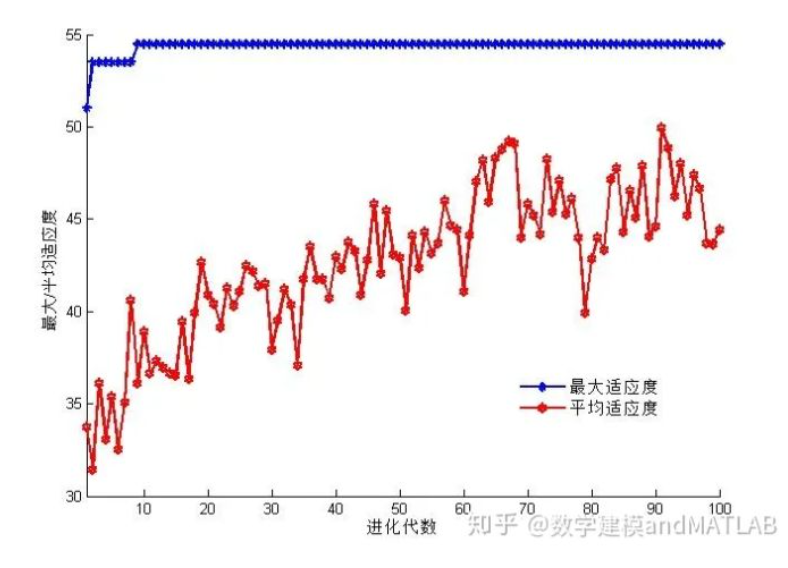
当平均适应度接近最大适应度时,种群中每个个体的基因趋同,再没有进化的必要,可以认为算法收敛,本次求解完成。由求解结果可知,我们在有900个积分的情况下,最多可兑换54.5元的商品,分别是:中杯可乐、中薯条1份、脆皮巧克力大圆筒、中热拿铁。
参考链接:https://www.zhihu.com/question/23293449/answer/1294327812
提交到集群
./bin/spark-submit —class com.example.gene.sample.SparkGA —master spark://202.112.151.58:7077 —executor-memory 10G —total-executor-cores 32 /root/study/20210619_2/gene.jar
ppt:并行遗传算法.pptx
Chromosome.javaGeneticAlgorithm.javaResultVO.javaSparkGA.java