一、优化问题:
优化:是应用数学的一个分支,主要研究在特定情况下最大化或最小化某一特定函数。
优化算法是在建立了数学模型之后不能求偏微分 or 不能通过求导的方式求得最小值时,采用一些优化算法能够解决问题。
二、遗传算法
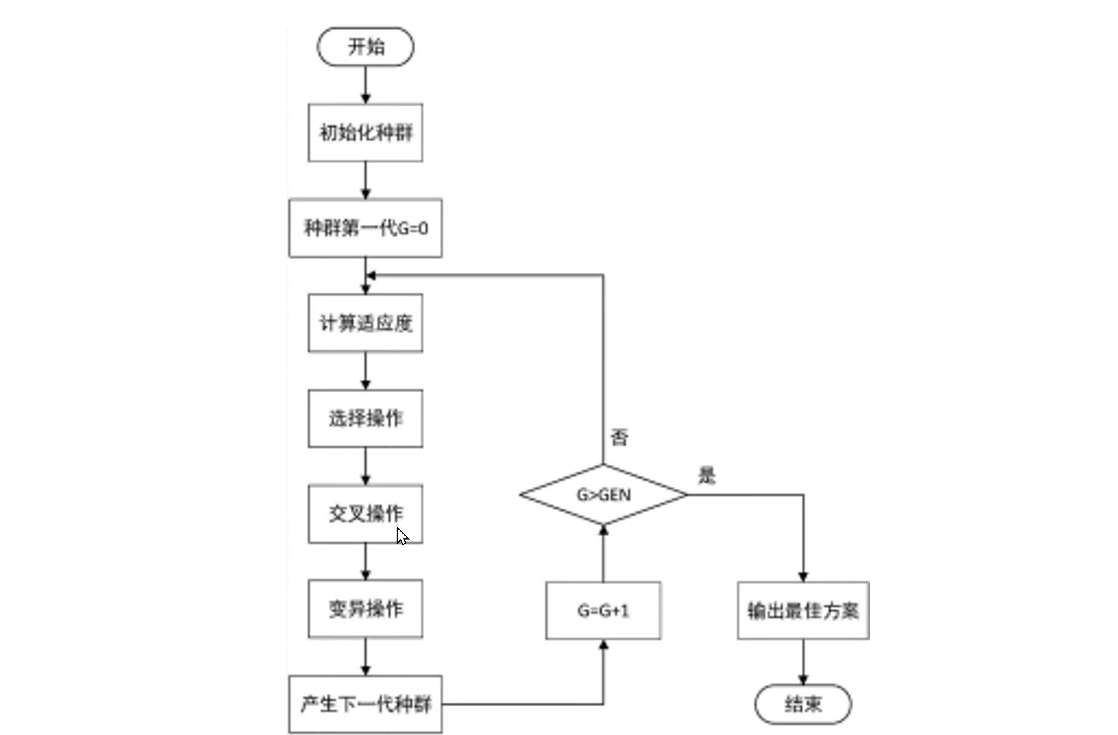
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化论过程的一种搜索(寻优)算法,在人工系统中实现特定目标的优化。实质是通过群体搜索技术,根据适者生存逐代进化最终得到最优解。
遗传算法必须做以下操作:初始群体的产生、求每一个个体的适应度、根据适者生存选择优良个体(选择)、选出的优良个体配对产生下一代群体(交叉、变异)、循环进行逐代进化直到满足中止条件。
| 生物遗传概念 | 遗传算法中的作用 |
|---|---|
| 适者生存 | 算法停止时,最优目标值的可行解有最大的可能被留住 |
| 个体 | 可行解 |
| 染色体 | 可行解的编码 |
| 基因 | 可行解中每一分量的特征 |
| 适应性 | 适应度函数 |
| 种群 | 根据适应度函数选取的一组可行解 |
| 交配 | 通过交配原则产生一组新的可行解 |
| 变异 | 编码的某一分量发生变化的过程 |
1.遗传算法原理
(1)选择操作:
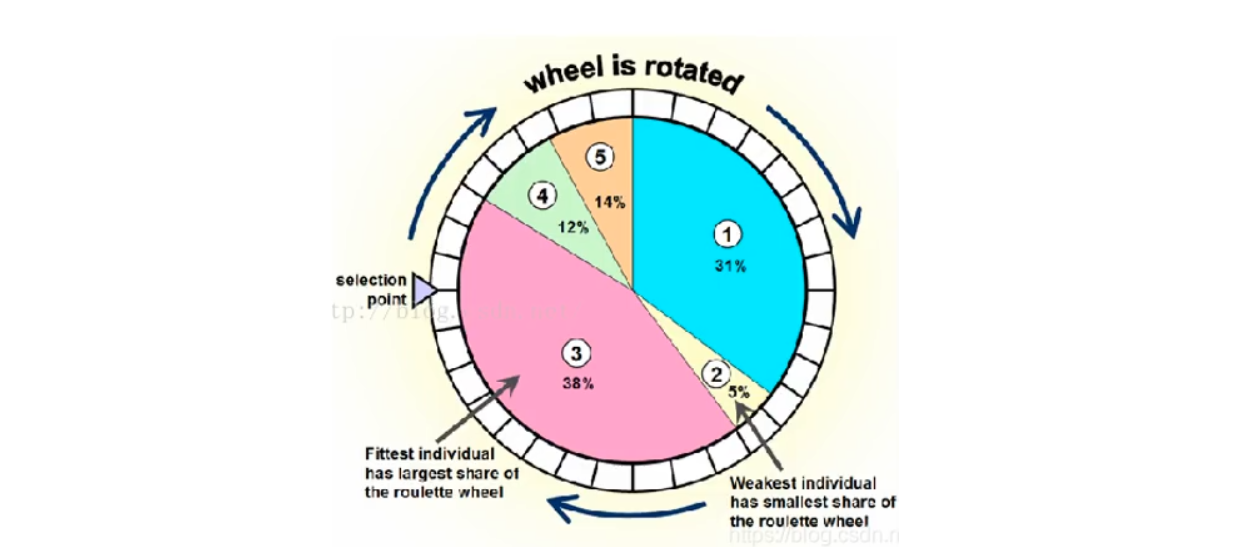
轮盘法,基于适应度比例的选择策略,个体i被选中的概率为:个体被选中的概率 = 个体适应度函数值 / 所有个体适应度函数值总和
(2)交叉操作:
交叉操作采用单点交叉,第k个染色体 ak 和第l个染色体 al 在j位的交叉操作方法为,b为[0, 1]随机数:
%2Ba%7Blj%7D(b)%0A#card=math&code=a%7Bkj%7D%3Da%7Bkj%7D%281-b%29%2Ba%7Blj%7D%28b%29%0A&id=U8iBw)
%2Ba%7Bkj%7D(b)%0A#card=math&code=a%7Blj%7D%3Da%7Blj%7D%281-b%29%2Ba%7Bkj%7D%28b%29%0A&id=aTYL7)
(3)变异操作:
变异是实现群体多样性的一种手段,也是全局寻优的保证。
第i个个体的第j个基因 aij 进行变异操作的方法为,r为[0, 1]随机数,gen为当前迭代次数,genmax为最大迭代次数:
*(1-G(gen))%2C
r%3C%3D0.5%0A#card=math&code=a%7Bij%7D%3Da%7Bij%7D-%28a%7Bij%7D-a%7Bmin%7D%29%2A%281-G%28gen%29%29%2Cr%3C%3D0.5%0A&id=V7a3B)
*(1-G(gen))%2C
r%3E%3D0.5%0A#card=math&code=a%7Bij%7D%3Da%7Bij%7D%2B%28a%7Bmax%7D-a%7Bij%7D%29%2A%281-G%28gen%29%29%2Cr%3E%3D0.5%0A&id=HXAId)
其中关于G(gen)函数有:
%3Dr(1-%5Cfrac%7Bgen%7D%7Bgenmax%7D)%5E2%0A#card=math&code=G%28gen%29%3Dr%281-%5Cfrac%7Bgen%7D%7Bgenmax%7D%29%5E2%0A&id=wUx7o)
2.遗传算法MATLAB实现
(1)主程序Genetic.m
用于求解的遗传算法参数设定如下:
种群大小M=50;最大代数G=1000;
交叉率Pc=1;交叉概率为1能保证种群的充分进化
变异率Pm=0.1;一般而言,变异发生的可能性较小
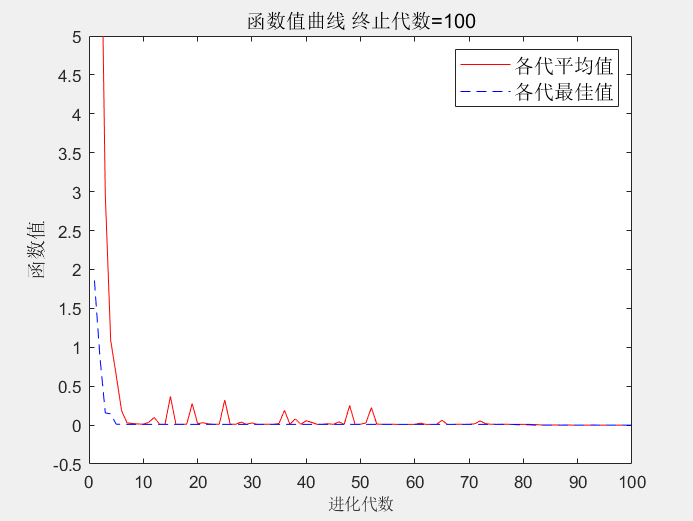
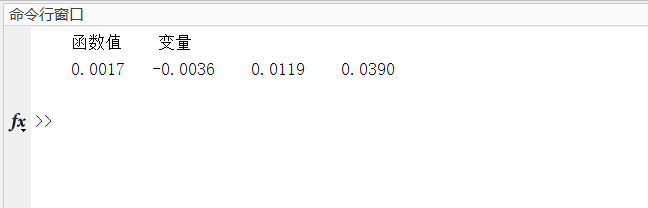
% 前置参数设定maxgen = 100;sizepop = 50;pcross = 0.6;pmutation = 0.01;% 假定目标函数为y = x1^2 + x2^2 + x3^2;lenchrom = [1, 1, 1];% 假定约束条件都为[-5, 5]bound = [-5, 5; -5, 5; -5, 5];% 自定义结构体变量individuals = struct('fitness', zeros(1, sizepop), 'chrom', []);avgfitness = [];bestfitness = [];bestchrom = [];% 1.初始化种群% (1)初始化种群for i = 1 : sizepop% Code函数作用:根据给定的基因的数量和范围初始化种群individuals.chrom(i, :) = Code(lenchrom, bound);% 计算适应度函数x = individuals.chrom(i, :);individuals.fitness(i) = func(x);end% (2)找出目前初始种群中适应度(即目标函数)最小的情况,记录其bestfitness与bestindex[bestfitness, bestindex] = min(individuals.fitness);bestchrom = individuals.chrom(bestindex, :);avgfitness = sum(individuals.fitness) / sizepop;% (3)定义一个变量来记录最好的fitness与avgfitness的变化情况trace = [];% 2.进入程序核心部分for i = 1 : maxgen% (1)利用Select函数进行选择操作individuals = Select(individuals, sizepop);% (2)利用Cross函数进行交叉操作individuals.chrom = Cross(pcross, lenchrom, individuals.chrom, sizepop, bound);% (3)利用Mutation函数进行变异操作individuals.chrom = Mutation(pmutation, lenchrom, individuals.chrom, sizepop, [i,maxgen], bound);% (4)计算适应度函数的值for j = 1 : sizepopx = individuals.chrom(j, :);individuals.fitness(j) = func(x);end% (5)找出目前种群中适应度(即目标函数)最小的情况,并动态更新最优值[temp_bestfitness, temp_bestindex] = min(individuals.fitness);if bestfitness > temp_bestfitnessbestfitness = temp_bestfitness;bestchrom = individuals.chrom(temp_bestindex, :);endavgfitness = sum(individuals.fitness) / sizepop;% (6)记录最好的fitness与avgfitness的变化情况trace = [trace;[avgfitness, bestfitness]];endfigureplot((1 : maxgen)', trace(:,1), 'r-', (1 : maxgen)', trace(:,2), 'b--');title(['函数值曲线 ' '终止代数=' num2str(maxgen)], 'fontsize', 12);xlabel('进化代数', 'fontsize', 10);ylabel('函数值', 'fontsize', 12);legend('各代平均值','各代最佳值','fontsize', 12);ylim([-0.5, 5])disp('函数值 变量');disp([bestfitness, x]);
(2)初始化群体Code.m
% Code——初始化种群函数function ret = Code(lenchrom, bound)flag = 0;while flag == 0% 1.随机生成一个1行3列的随机数数组pick = rand(1, length(lenchrom));% 2.更改随机数组的数据范围为[-5, 5]ret = bound(:, 1)' + (bound(:, 2) - bound(:, 1))' .* pick;% 3.利用test函数检测交叉操作后的数据是否合格flag = test(lenchrom, bound, ret);end
(3)目标函数func.m
% func——目标函数(计算fitness适应度函数)function y = func(x)y = sum(x .^ 2);
(4)选择操作Select.m
% Select——选择操作函数function ret = Select(individuals, sizepop)% 1.个体被选中的概率 = 个体适应度函数值 / 所有个体适应度函数值总和individuals.fitness = 1 ./ individuals.fitness;sumfitness = sum(individuals.fitness);posib = individuals.fitness / sumfitness;% 定义一个index变量用于存放被选中的个体index = [];% 2.利用轮盘法确定选中个体for i = 1 : sizepop% (1)生成一个pick随机数pick = rand;while pick == 0pick = rand;end% (2)判断是否被选中for j = 1 : sizepoppick = pick - posib(j);if pick < 0% 将个体j添加到被选中个体列表中index = [index, j];breakendendend% 3.将选中的所有个体返回individuals.chrom = individuals.chrom(index, :);individuals.fitness = individuals.fitness(index);ret = individuals;
(5)交叉操作Cross.m
% Cross——交叉操作函数function ret = Cross(pcross, lenchrom, chrom, sizepop, bound)% 对个体进行交叉操作for i = 1 : sizepop% 1.生成一个1行2列的随机数,因为是两个个体进行交叉pick = rand(1, 2);while prod(pick) == 0pick = rand(1, 2);end% 2.通过随机生成index实现交叉个体的随机选择index = ceil(pick .* sizepop);% 3.通过随机生成pick与pcross进行比较判定两个体是否进行交叉pick = rand;while pick == 0pick = rand;endif pick > pcrosscontinue;end% 4.选择两个个体在哪一个位点进行交叉flag = 0;while flag == 0%(1)确定两个个体交叉的位点pick = rand;while pick == 0pick = rand;endpos = ceil(pick .* sum(lenchrom));%(2)进行交叉操作pick = rand;v1 = chrom(index(1), pos);v2 = chrom(index(2), pos);chrom(index(1), pos) = pick * v2 + (1 - pick) * v1;chrom(index(2), pos) = pick * v1 + (1 - pick) * v1;%(3)检测交叉操作后的染色体是否合格flag1 = test(lenchrom, bound, chrom(index(1), :));flag2 = test(lenchrom, bound, chrom(index(2), :));if flag1 * flag2 == 0flag = 0;elseflag = 1;endendendret = chrom;
(6)变异操作Mutation.m
% Mutation——变异操作函数function ret = Mutation(pmutation, lenchrom, chrom, sizepop, pop, bound)% 对个体进行变异操作for i = 1 : sizepop% 1.通过随机生成数pick确定变异个体pick = rand;while pick == 0pick = rand;endindex = ceil(pick * sizepop);% 2.通过随机生成pick与pmutation进行比较判定该个体是否进行变异pick = rand;if pick > pmutationcontinue;end% 3.选择个体在哪一个位点进行变异flag = 0;while flag == 0%(1)确定个体变异的位点pick = rand;while pick == 0pick = rand;endpos = ceil(pick * sum(lenchrom));%(2)进行变异操作v = chrom(i, pos);v1 = v - bound(pos, 1);v2 = bound(pos, 2) - v;pick = rand;if pick > 0.5delta = v2 * (1 - pick ^ ((1 - pop(1) / pop(2)) ^ 2));chrom(i, pos) = v + delta;elsedelta = v1 * (1 - pick ^ ((1 - pop(1) / pop(2)) ^ 2));chrom(i, pos) = v - delta;endflag = test(lenchrom, bound, chrom(i, :));endendret = chrom;
(7)test.m
% test——检测函数function flag = test(lenchrom, bound, code)flag = 1;[n, ~] = size(code);for i = 1 : nif code(i) < bound(i, 1) || code(i) > bound(i, 2)flag = 0;endend
3.遗传算法的改进
遗传算法的缺陷出现在交叉、变异操作,这些操作很可能会将优秀基因个体给变异掉(丢失最优解)。
算法改进:采用遗传算法精英库的策略:将交叉、突变后的子代与父代同时保留,对其进行排序比较留下精英部分。
function newPopulation = elitism(population, Er)M = length(population, Chromosomes);Elite_no = round(M * Er);[~, index] = sort(population, Chromosomes(:).fitness, 'descend');for k = 1 : Elite_nonewPopulation.Chromosomes(k).Gene = populationn.Chromosomes(index(k)).Gene;newPopulation.Chromosomes(k).fitness = populationn.Chromosomes(index(k)).fitness;endend
三、粒子群算法
粒子群算法主要是在模拟鸟类觅食的行为:一群鸟在随机搜索食物(在这个区域里只有一块食物、所有鸟都不知道食物位置、但他们知道离食物还有多远),找到食物的最优策略采用搜索离食物最近的鸟的周围区域——粒子群算法。
食物:目标函数的最小值、鸟的位置:代表决策变量、
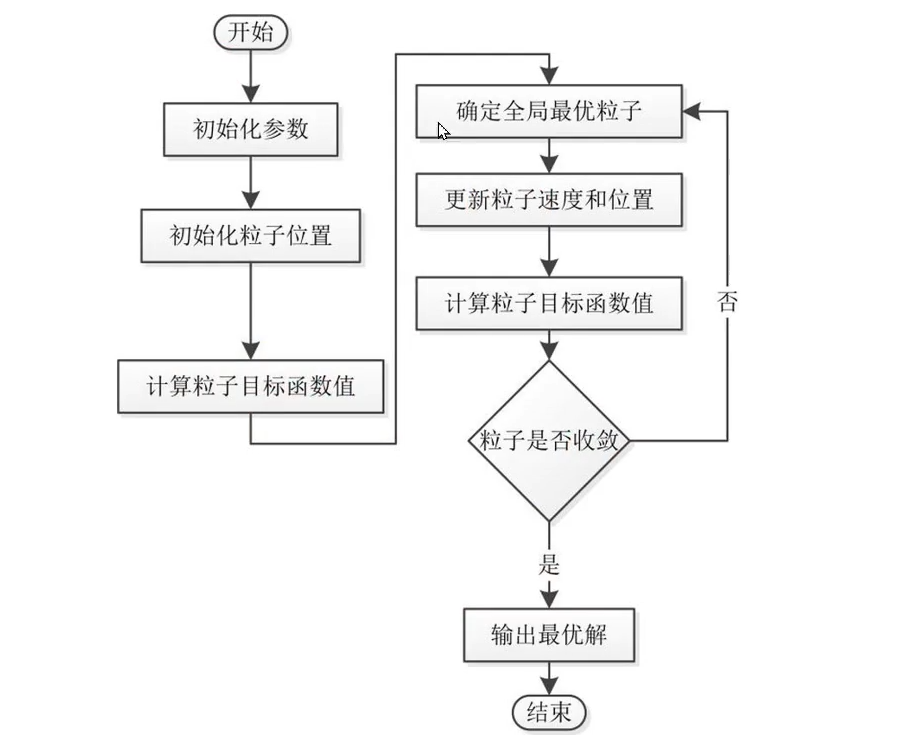
粒子群算法必须做以下操作:初始群体的产生、计算粒子目标函数值、确定全局最优粒子、更新速度和位置(核心操作)、粒子是否收敛(是否满足中止条件)。
1.粒子群算法原理
(1)速度与位置的更新操作:
由n只鸟组成的种群B = (B1, B2, B3, ..., Bn),其中第i只鸟Bi的位置可表示为Xi = [Xi1, Xi2, Xi3, ..., Xid];其速度为Vi = [Vi1, Vi2, Vi3, ..., Vid],则第t + 1次迭代中鸟类的位置与速度可更新为:
t + 1时刻的位置 = t时刻位置+t + 1时刻速度方向
t + 1时刻速度 = ω常数 * t时刻速度(速度惯性向) + 个体自信方向 + 全局最优方向
%2Bc%7B2%7Dr%7B2%7D(G%5Et%7Bbest%7D-X%5Et_i)%0A#card=math&code=V%5E%7Bt~%2B~1%7D_i%3D%CF%89V%5Et_i%2Bc%7B1%7Dr%7B1%7D%28P%5Et%7Bibest%7D-X%5Eti%29%2Bc%7B2%7Dr%7B2%7D%28G%5Et%7Bbest%7D-X%5Et_i%29%0A&id=g0PCm)
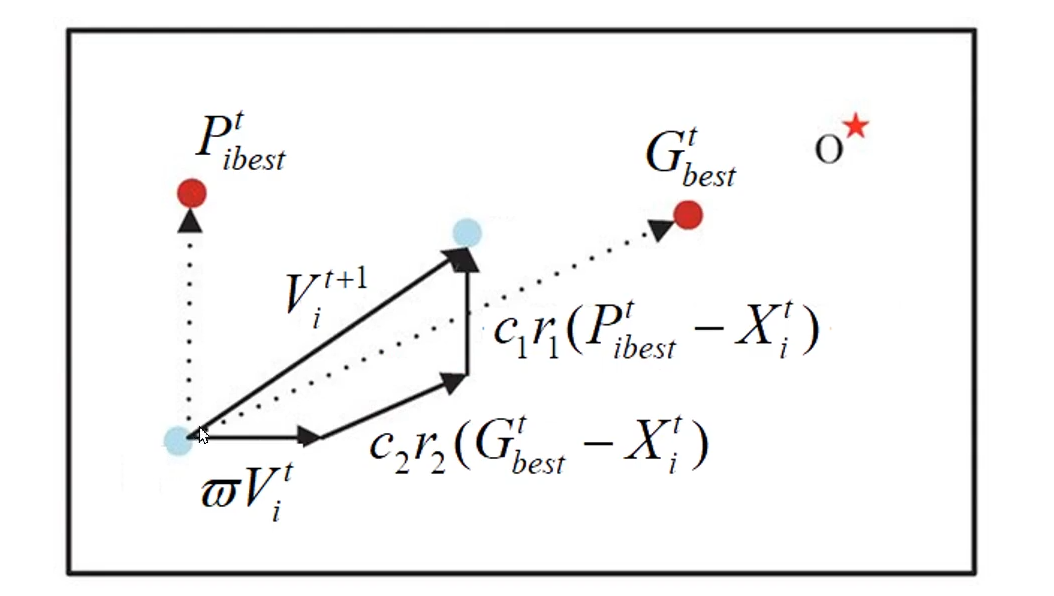
(2)区分全局最优gbest与个体最优pbest的概念:
全局最优:在一个种群中,所有的鸟在某一代中 or 在某个时刻中所能找到的最优值,gbest为1组数字(位置)。
个体最优:针对每一个体,某一只鸟从第1代到第 i 代这个过程中,该鸟所找到的最优值,pbest为n组数字(位置)。
补充:详细可使用matlab查看粒子群算法运行中产生的参数gbest和pbest变量,进行进一步理解
2.粒子群算法MATLAB实现
程序结构:
(1)主程序PSO.m:
clcclearc1 = 1.49445;c2 = 1.49445;w = 1;maxgen = 200;sizepop = 50;nVar = 2; % 变量的数量Vmax = 5; % 速度的范围为[-10, 10],根据popmax进行确定Vmin = -5;popmax = 100; % 搜索的范围为[-100, 100]popmin = -100;% 1.初始鸟群的生成for i = 1 : sizepoppop(i, :) = (popmax - popmin) * rands(1, nVar) + popmin;%(1)初始速度的生成V(i, :) = (Vmax - Vmin) * rands(1, nVar) + Vmin;%(2)计算目标函数fitness(i) = func(pop(i, :));end% 2.找到全局最优与个体最优粒子[bestfitness, bestindex] = max(fitness);%(1)初始更新全局最优与个体最优gbest = pop(bestindex, :);pbest = pop;fitnesspbest = fitness;fitnessgbest = bestfitness;for i = 1 : maxgen% 3.更新粒子速度与位置for j = 1 : sizepop%(1)更新粒子的速度V(j, :) = w .* V(j, :) + c1 * rand * (pbest(j, :) - pop(j, :)) + c2 * rand * (gbest - pop(j, :));%对飞行的最大速度进行限制V(j, find(V(j, :) > Vmax)) = Vmax;V(j, find(V(j, :) < Vmin)) = Vmin;%(2)更新粒子的位置pop(j, :) = pop(j, :) + V(j, :);%对粒子移动的位置进行限制pop(j, find(pop(j, :) > popmax)) = popmax;pop(j, find(pop(j, :) < popmin)) = popmin;%(3)找到目标函数值fitness(j) = func(pop(j, :));end%4.更新适目标函数最优值for j = 1 : sizepopif fitness(j) < fitnesspbest(j)pbest(j, :) = pop(j, :);fitnesspbest(j) = fitness(j);endif fitness(j) < fitnessgbestgbest = pop(j, :);fitnessgbest = fitness(j);endendyy(i) = fitnessgbest;endplot(yy)title('最优个体适应度', 'fontsize', 12);xlabel('进化代数', 'fontsize', 12);ylabel('适应度', 'fontsize', 12);disp('函数值 变量');disp([fitnessgbest, gbest]);
(2)目标函数func.m:
% func——目标函数function y = func(x)y = sum(x .^ 2);
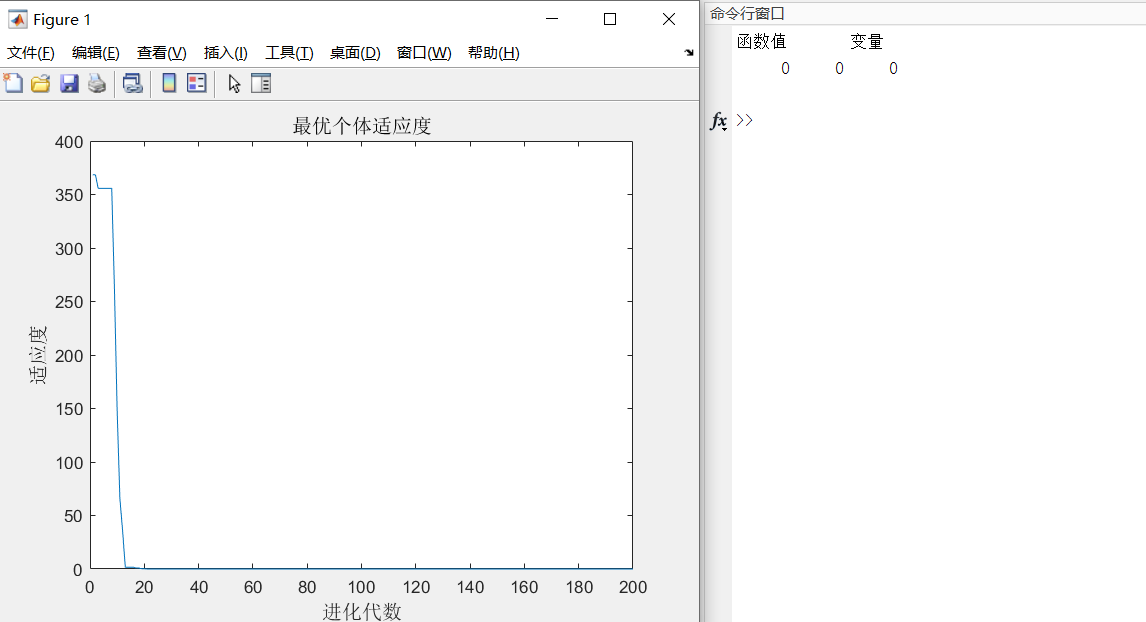
3.粒子群算法的改进
粒子群算法受到初始种群生成的影响较严重,如果初始种群生成不恰当将导致结果陷入局部最优解,而不是全局最优解。
算法改进:为避免粒子群陷入局部最优解,类比遗传算法应考虑为粒子群算法也加入基因变异的操作(粒子位置重新分布)。
4.补充:优化问题约束条件的处理

对于约束条件(包括等式约束、不等式约束)的处理,使用惩罚函数进行操作:
(1)惩罚函数:
用于解决约束条件下的最优化问题,通过惩罚函数可以将现有约束的目标函数转化为无约束的目标函数。
‘%3Df(x)%2BC%0A#card=math&code=f%28x%29%27%3Df%28x%29%2BC%0A&id=qeI79)
其中C为一个非常大的常数,相对于遗传算法、粒子群算法而言当个体被加上常数C时,就会被排除在最优解之外。
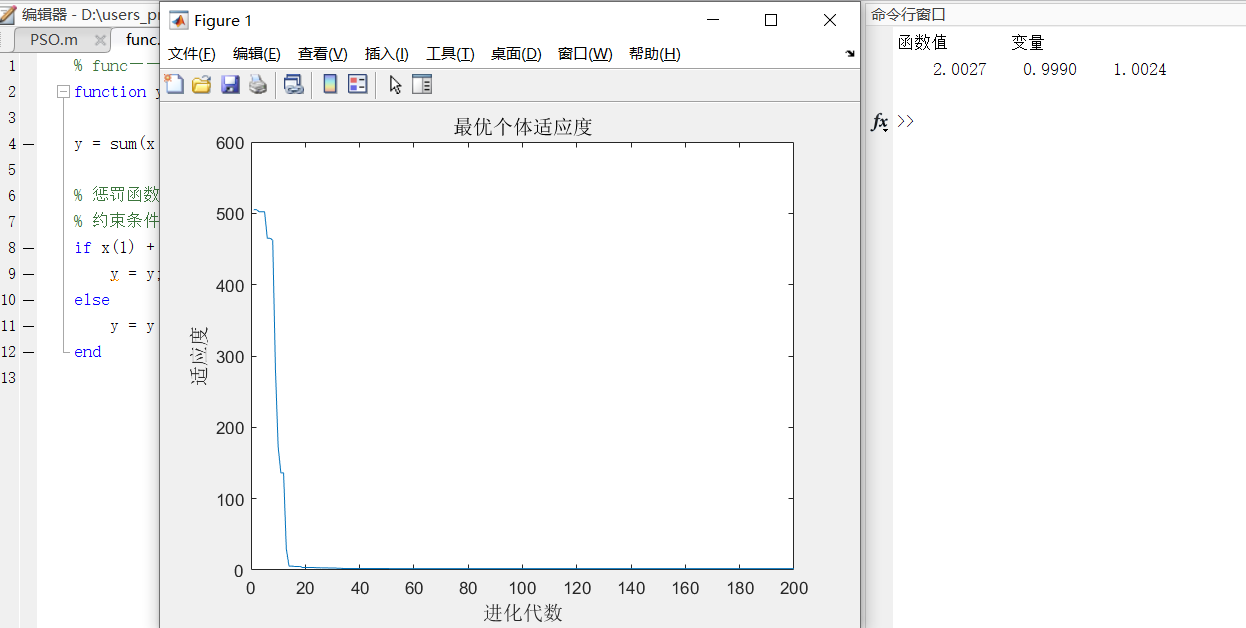
具体在粒子群算法上对程序进行修改后的结果为:
% func——目标函数function y = func(x)y = sum(x .^ 2);% 惩罚函数对约束条件进行处理% 约束条件:要求x1与x2相加的值应大于2,否则排除最优解if x(1) + x(2) > 2y = y;elsey = y + 1000;end
四、多目标优化问题
在实际问题中大都具有多个目标且需要同时满足,即在同一问题模型中同时存在几个非线性目标,而这些目标函数需要同时进行问题优化处理,而这些目标又往往是互相冲突的(必要),这类问题被称为多目标优化问题。
补充:多目标优化问题的解往往是多个解
1.多目标优化
(1)多目标优化关键概念:
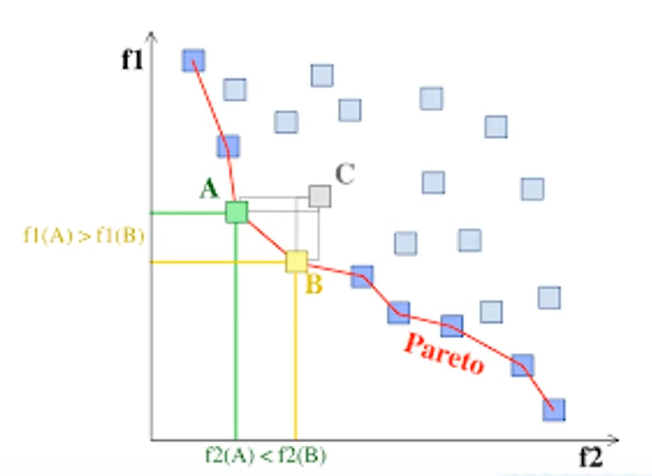
point1:支配
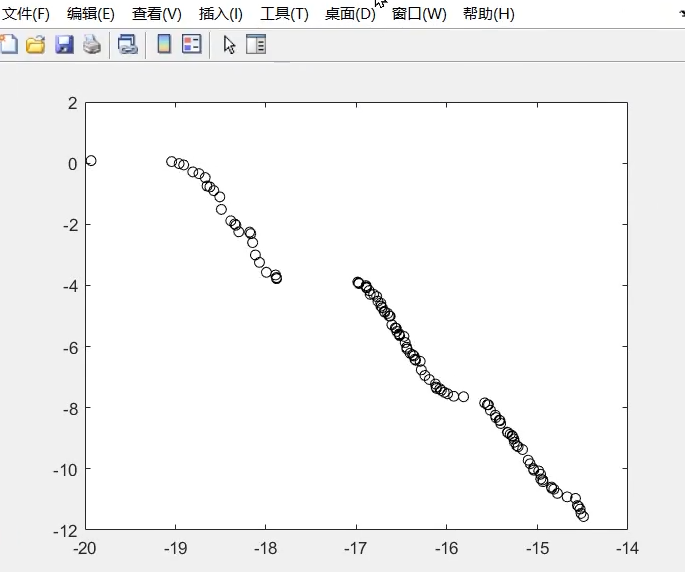
在多目标优化问题中,如果个体p至少有一个目标比个体q好,而且个体p的所有目标都不比个体q差,那么称个体p支配个体q(p>=q)。
如下图图例所示,图中可以看出个体A、B完全支配个体C(个体C将被淘汰),而个体A、B之间不存在支配关系。
point2:序值
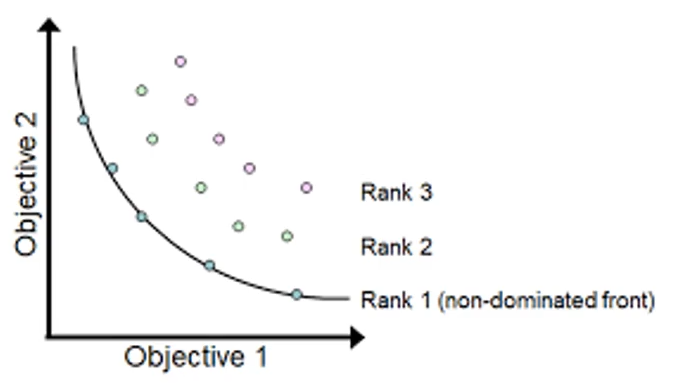
如果p支配q,那么p的序值比q低。如果p和q互补支配,那么p和q有相同的序值。
point3:拥挤距离
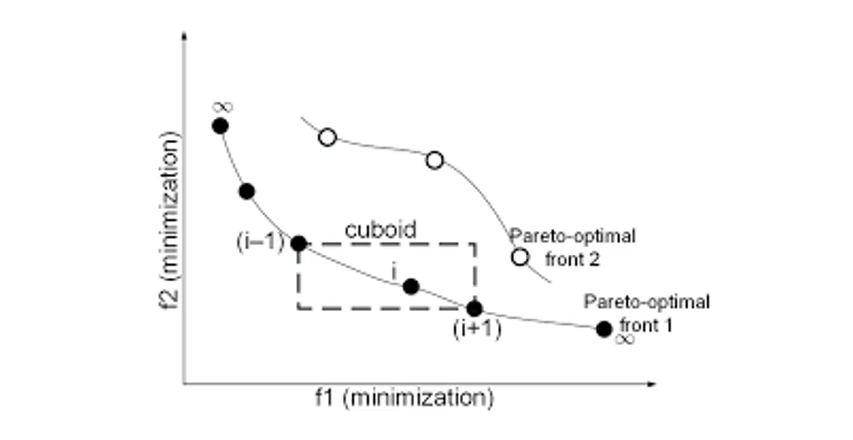
拥挤距离用来计算某前端中的某个体与该前端中其他个体之间的距离,用以表征个体间的拥挤程度。
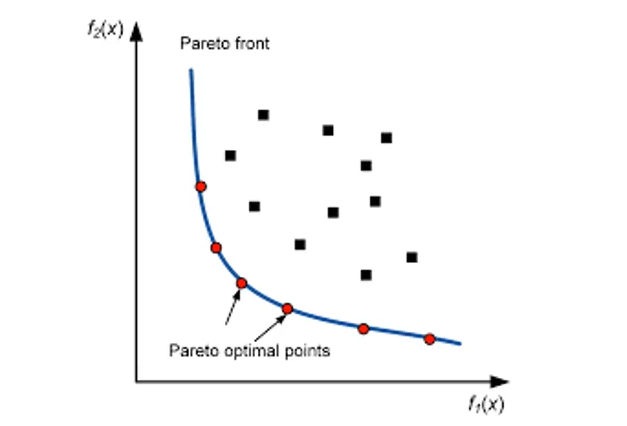
(2)多目标较单目标优化问题的难点:
- 全局最优与局部最优的选择
- 目标函数的计算(多个最优值的筛选与删除),涉及支配、拥挤距离问题,具体实现见代码演示
2.多目标优化代码实现:
以下的多目标优化问题使用粒子群优化算法解决,作为案例
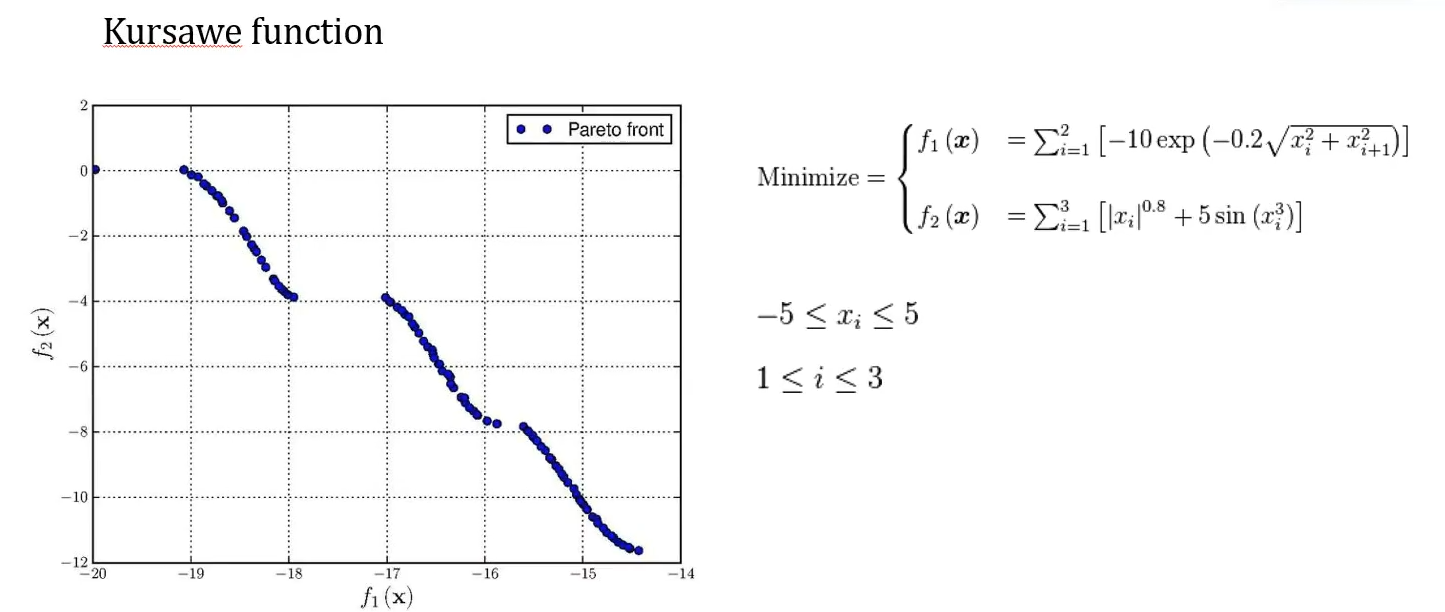
程序结构:
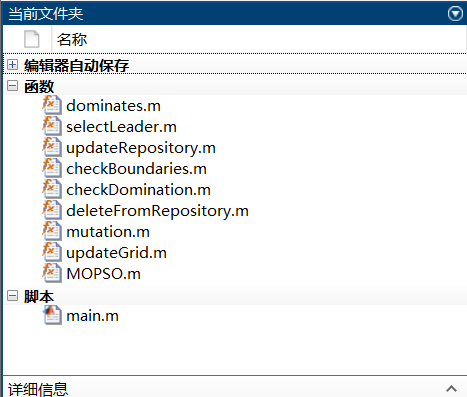
函数调用结构: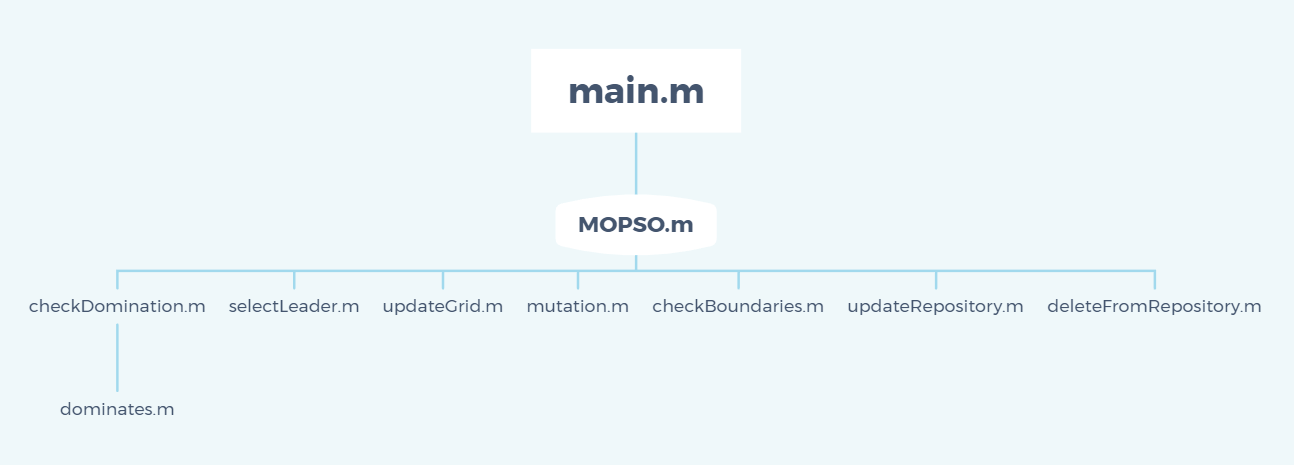
注意:同层次间的函数还存在相互调用的关系,图示中不做详细表示
(1)主程序main.m:
clearclc% 目标函数的表示描述MultiObj.func= @(x) [-10 .* (exp(-0.2 .* sqrt(x(:, 1) .^ 2 + x(:, 2) .^ 2)) + exp(-0.2 .* sqrt(x(:, 2) .^ 2 + x(:, 3) .^ 2))), sum(abs(x) .^ 0.8 + 5 .* sin(x .^ 3), 2)];MultiObj.nVar = 3;MultiObj.var_min = -5 .* ones(1, MultiObj.nVar);MultiObj.var_max = 5 .* ones(1, MultiObj.nVar);% 算法初始参数设置params.maxgen = 300;params.Np = 500;params.W = 0.4;params.C1 = 2;params.C2 = 2;params.maxvel = 5; % 设置最大速度params.u_mut = 0.5; % 设置变异率params.Nr = 40; % pareto前沿上保留的点数(最优值的选择数目)params.ngrid = 40; % 针对多目标优化设置拥挤距离% 将参数和程序传递给粒子群算法程序REP = MOPSO(params, MultiObj);
(2)多目标优化粒子群算法MOPSO.m:
function REP = MOPSO(params, MultiObj)% 粒子群算法本身设置参数的传递Np = params.Np;Nr = params.Nr; % 精英库的最大个体数目maxgen = params.maxgen;W = params.maxgen;C1 = params.C1;C2 = params.C2;ngrid = params.ngrid;maxvel = params.maxvel;u_mut = params.u_mut;% 目标函数的传递func = MultiObj.func;nVar = MultiObj.nVar;var_min = MultiObj.var_min(:);var_max = MultiObj.var_max(:);% 1.初始化种群的参数POS = repmat((var_max-var_min)', Np, 1) .* rand(Np, nVar) + repmat(var_min', Np, 1);% 2.初始化粒子运动速度为0VEL = zeros(Np, nVar);% 3.通过目标函数计算当前位置的适应度情况POS_fit = func(POS);% 4.选出个体最优与全局最优的位置信息及适应度函数PBEST = POS;PBEST_fit = POS_fit;% 5.找出多个最小值(最优解),返回0/1矩阵DOMINATED = checkDomination(POS_fit);% 6.具有支配能力的个体保留REP.pos = POS(~DOMINATED, :);REP.pos_fit = POS_fit(~DOMINATED, :);% 7.种群进行网格更新REP = updateGrid(REP, ngrid);maxvel = (var_max - var_min) .* maxvel ./ 100;gen = 1;display(['Generation #0 - Repository size:' num2str(size(REP.pos, 1))]);% 8.进入循环中进行若目标的位置、速度更新处理stopCondition = false;while ~stopConditionh = selectLeader(REP);%(1)更新速度VEL = W .* VEL + C1 * rand(Np, nVar) .* (PBEST - POS) + C2 * rand(Np, nVar) .* (repmat(REP.pos(h, :), Np, 1) - POS);%(2)更新位置信息POS = POS + VEL;%(3)使用变异操作对粒子群算法进行优化POS = mutation(POS, gen, maxgen, Np, var_max, var_min, nVar, u_mut);%(4)test检测变异后的粒子是否超出限制范围[POS, VEL] = checkBoundaries(POS, VEL, maxvel, var_max, var_min);%(5)计算目标函数POS_fit = func(POS);%(6)更新pareto前沿的记忆库REP = updateRepository(REP, POS, POS_fit, ngrid);if(size(REP.pos, 1) > Nr)% 根据拥挤距离控制精英库中的个体个数% 如果精英库中的个体数目大于设置的最大个体数目Nr,则删除部分个体REP = deleteFromRepository(REP, size(REP.pos, 1) - Nr, ngrid);end%(7)更新个体最优pos_best = dominates(POS_fit, PBEST_fit); %检测支配关系best_pos = ~dominates(PBEST_fit, POS_fit);best_pos(rand(Np, 1) >= 0.5) = 0; %如果没有完全支配关系,则随机选择最优if(sum(pos_best) > 1) % 如果为完全支配关系,则直接替换掉PBEST_fit(pos_best, :) = POS_fit(pos_best, :);PBEST(pos_best, :) = POS(pos_best, :);endif(sum(best_pos) > 1)PBEST_fit(best_pos, :) = POS_fit(best_pos, :);PBEST(best_pos, :) = POS(best_pos, :);enddisplay(['Generation #' num2str(gen) '- Repository size:' num2str(size(REP.pos, 1))]);%(8)迭代次数增加1,判断是否结束循环迭代gen = gen + 1;if gen > maxgenstopCondition = true;endendh_rep = plot(REP.pos_fit(:, 1), REP.pos_fit(:, 2), 'ok');end
(3)根据网格质量选区最优selectLeader.m:
% selectLeader——在网格中随机选择一个个体作为全局最优解function selected = selectLeader(REP)% 计算总和网格质量总和prob = cumsum(REP.quality(:, 2));sel_hyp = REP.quality(find(rand(1, 1) * max(prob) <= prob, 1, 'first'), 1);idx = 1 : 1 : length(REP.grid_idx);% 类似轮盘法生产随机数selected = idx(REP.grid_idx == sel_hyp);selected = selected(randi(length(selected)));end
(4)更新精英库updateRepository.m:
如何更新精英库涉及支配问题、拥挤距离问题
function REP = updateRepository(REP, POS, POS_fit, ngrid)% 更新记忆库实际上就是更新支配%(1)进行第一次支配检验,检验新的个体DOMINATED = checkDomination(POS_fit);REP.pos = [REP.pos; POS(~DOMINATED, :)];REP.pos_fit = [REP.pos_fit; POS_fit(~DOMINATED, :)];%(2)进行第二次支配检验,在包括原始个体的精英库中进行检验DOMINATED = checkDomination(REP.pos_fit);REP.pos_fit = REP.pos_fit(~DOMINATED, :);REP.pos = REP.pos(~DOMINATED, :);%(3)更新网格质量为下一次选择Leader做准备REP = updateGrid(REP, ngrid);end
(5)检测越界函数checkBoundaries.m:
function [POS, VEL] = checkBoundaries(POS, VEL, maxvel, var_max, var_min)Np = size(POS, 1);MAXLIM = repmat(var_max(:)', Np, 1);MINLIM = repmat(var_min(:)', Np, 1);MAXVEL = repmat(maxvel(:)', Np, 1);MINVEL = repmat(-maxvel(:)', Np, 1);VEL(VEL > MAXVEL) = MAXVEL(VEL > MAXVEL);VEL(VEL < MINVEL) = MINVEL(VEL < MINVEL);VEL(POS > MAXLIM) = (-1) .* VEL(POS > MAXLIM);POS(POS > MAXLIM) = MAXLIM(POS > MAXLIM);% 优化:当鸟飞到边界时碰撞,将鸟的速度置反方向VEL(POS < MINLIM) = (-1) .* VEL(POS < MINLIM);POS(POS < MINLIM) = MINLIM(POS < MINLIM);end
(6)检测支配函数checkDomination.m:
function dom_vector = checkDomination(fitness)% checkDomination函数式在目标函数fitness传入后的处理% 最后输出的向量是0/1值,如果个体被支配则输出1,否则输出0% 1.定义种群的个数Np = size(fitness, 1);% 2.定义0/1dom_vector向量用于决定哪些进入精英解中(是否被支配)dom_vector = zeros(Np, 1);% 3.将正常的排列组合与其倒序的组合在一起,用于判定all_perm = nchoosek(1 : Np, 2);all_perm = [all_perm; [all_perm(:, 2), all_perm(:, 1)]];% 4.判断是否为支配关系操作d = dominates(fitness(all_perm(:, 1), :), fitness(all_perm(:, 2), :));% 处理0/1向量中的重复值去掉dominated_particles = unique(all_perm(d == 1, 2));% 留下哪几个个体是优秀的个体dom_vector(dominated_particles) = 1;end
(7)dominates.m:
% dominates——判断两个体是否具有支配关系function d = dominates(x, y)% 根据支配的基本概念进行判断d = all(x <= y, 2) & any(x < y, 2);end
(8)删除精英库个体函数deleteFromRepository.m:
function REP = deleteFromRepository(REP, n_extra, ngrid)% 传入参数解释:REP:精英库、n_extra:多余的个体数量、ngrid:网格% 1.定义一个拥挤距离的初始值全为0的矩阵,代表相邻两个个体之间的距离crowding = zeros(size(REP.pos, 1), 1);for m = 1 : 1 : size(REP.pos_fit, 2)%(1)对第一个维度的目标函数值进行升序排列[m_fit, idx] = sort(REP.pos_fit(:, m), 'ascend');m_up = [m_fit(2 : end); Inf];m_down = [Inf; m_fit(1 : end - 1)];distance = (m_up - m_down) ./ (max(m_fit) - min(m_fit));[~, idx] = sort(idx, 'ascend');%(2)计算拥挤距离相加crowding = crowding + distance(idx);endcrowding(isnan(crowding)) = Inf;% 2.对拥挤距离进行升序排列[~, del_idx] = sort(crowding, 'ascend');%(1)删除精英库中多余的个体(拥挤距离太小的个体)del_idx = del_idx(1 : n_extra);REP.pos(del_idx, :) = [];REP.pos_fit(del_idx, :) = [];REP = updateGrid(REP, ngrid);end
(9)粒子群算法优化*:变异操作mutation.m:
function POS = mutation(POS, gen, maxgen, Np, var_max, var_min, nVar, u_mut)% 1.将整个种群分为3部分fract = Np / 3 - floor(Np / 3);if fract < 0.5sub_sizes = [ceil(Np / 3), round(Np / 3), round(Np / 3)];elsesub_sizes = [round(Np / 3), round(Np / 3), floor(Np / 3)];endcum_sizes = cumsum(sub_sizes);% 2.对于第2阶段个体做均匀变异处理nmut = round(u_mut * sub_sizes(2));if nmut > 0idx = cum_sizes(1) + randperm(sub_sizes(2), nmut);% 粒子群算法的基因变异处理(完全初始化代表基因变异)POS(idx, :) = repmat((var_max - var_min)', nmut, 1) .* rand(nmut, nVar) + repmat(var_min', nmut, 1);end% 3.对于第3阶段进行不均匀变异操作per_mut = (1 - gen / maxgen) ^ (5 * nVar); % 突变率逐渐降低nmut = round(per_mut * sub_sizes(3));if nmut > 0idx = cum_sizes(2) + randperm(sub_sizes(3), nmut);POS(idx, :) = repmat((var_max - var_min)', nmut, 1) .* rand(nmut, nVar) + repmat(var_min', nmut, 1);endend
(10)更新网格操作updateGrid.m:
% updateGrid——更新网格:将所在空间划分成网格,为下一步选择全局最优or局部最优方向做好准备function REP = updateGrid(REP, ngrid)% 1.确定多目标有几个目标函数,确定在画网格空间的维数ndim = size(REP.pos_fit, 2);% 2.选取网格作为全局最优所在的网格REP.hypercube_limits = zeros(ngrid + 1, ndim);% 3.网格划分的格数+1for dim = 1 : ndimREP.hypercube_limits(:, dim) = linspace(min(REP.pos_fit(:, dim)), max(REP.pos_fit(:, dim)), ngrid + 1)';end% 4.判断有多少个pareto前沿上的点(多少个优秀的个体)npar = size(REP.pos_fit, 1);% 5.对优秀的个体进行寻找REP.grid_idx = zeros(npar, 1);REP.grid_subidx = zeros(npar, ndim);for n = 1 : 1 : nparidnames = [];for d = 1 : 1 : ndimREP.grid_subidx(n, d) = find(REP.pos_fit(n, d) <= REP.hypercube_limits(:, d)', 1, 'first') - 1;if(REP.grid_subidx(n, d) == 0)REP.grid_subidx(n, d) = 1;endidnames = [idnames ',' num2str(REP.grid_subidx(n, d))];endREP.grid_idx(n) = eval(['sub2ind(ngrid .* ones(1, ndim)' idnames ');']);end% 6.求算网格的质量,网格中鸟的数量越多质量越低,被选中的概率越低REP.quality = zeros(ngrid, 2);ids = unique(REP.grid_idx);for i = 1 : length(ids)REP.quality(i, 1) = ids(i);REP.quality(i, 2) = 10 / sum(REP.grid_idx == ids(i));endend
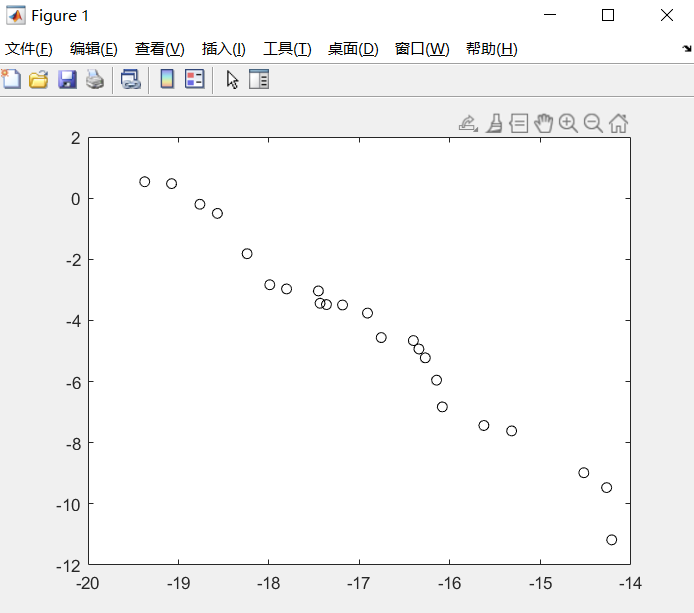
疑问:多目标优化问题粒子算法实现最后的结果与正确结果相差较大?
3.多目标优化结果处理