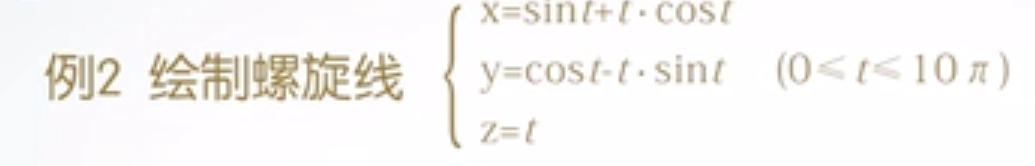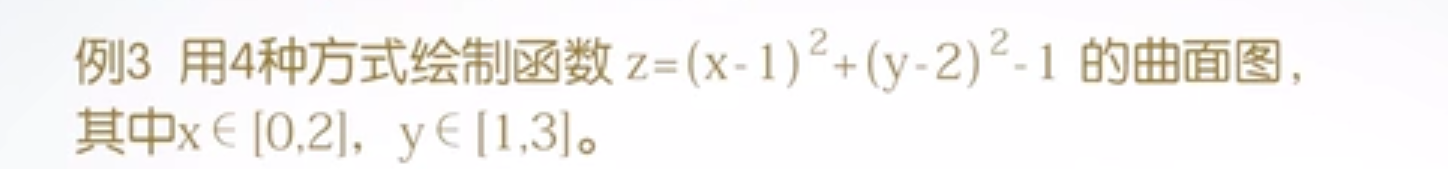三、MATLAB绘图
1.二维曲线
(1)plot函数:
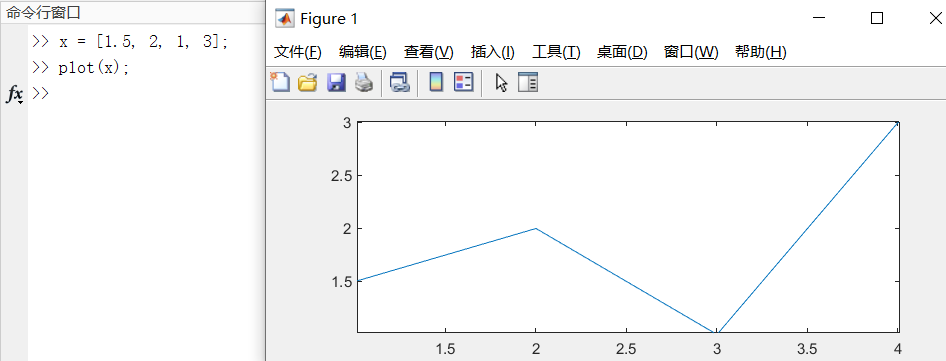
case1:plot(x)
当向量x为实数向量时,plot(x)以该向向量元素的下标为横坐标,元素的值为纵坐标绘制一条曲线。
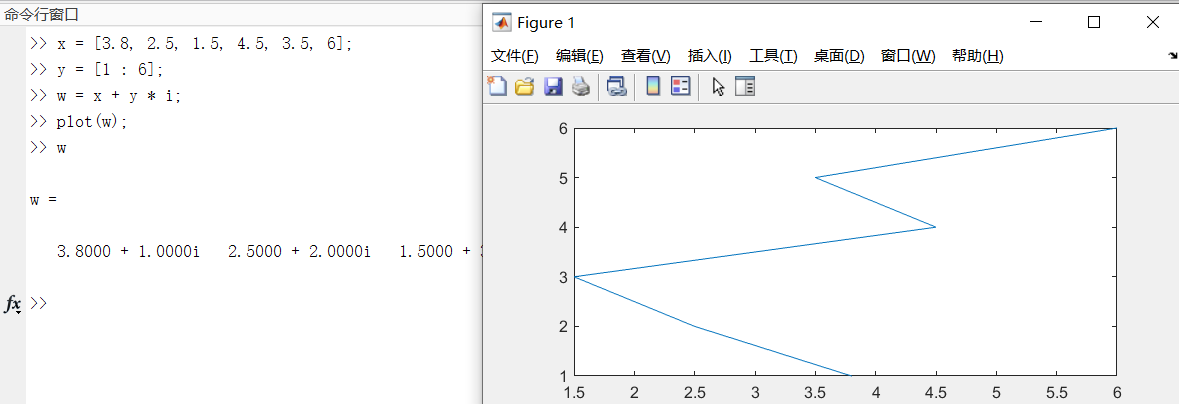
当向量x为复数向量时,plot(x)以该向的实部、虚部为横轴坐标绘制出一条曲线。
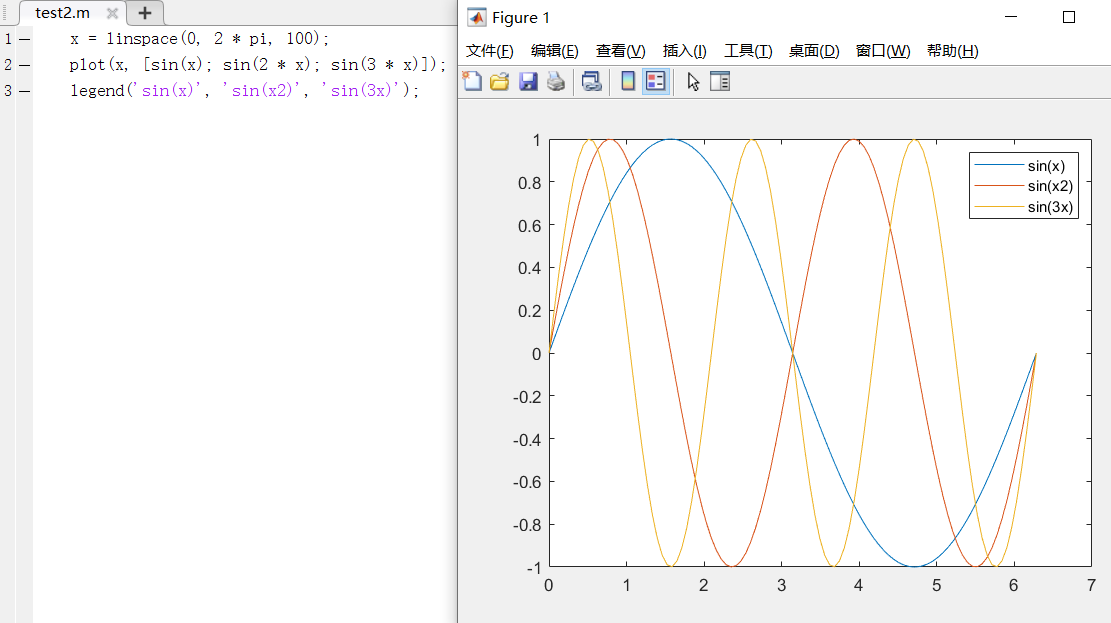
case2:plot(x,y),x、y为向量
当 x 是向量,y 是向量时:
其中x、y的分别用于存储x坐标和y坐标的数据,通常 x 和 y 为长度相等的向量。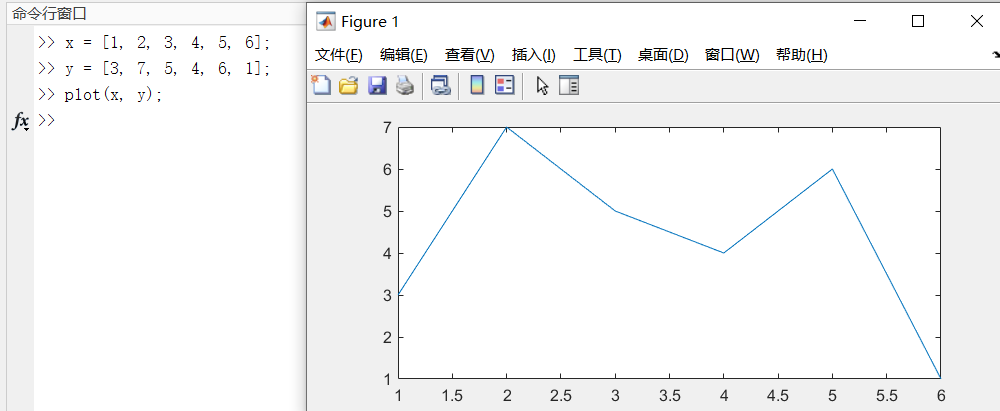
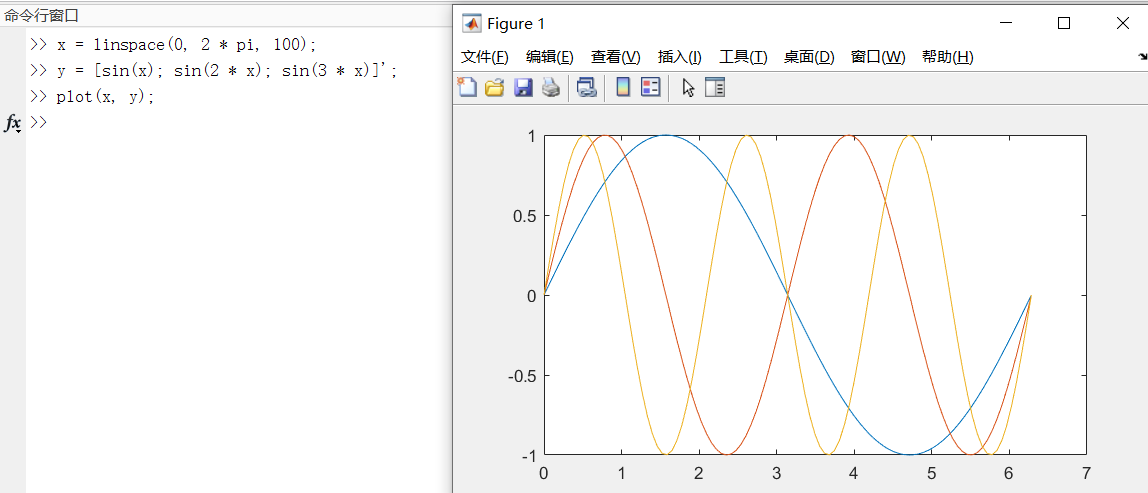
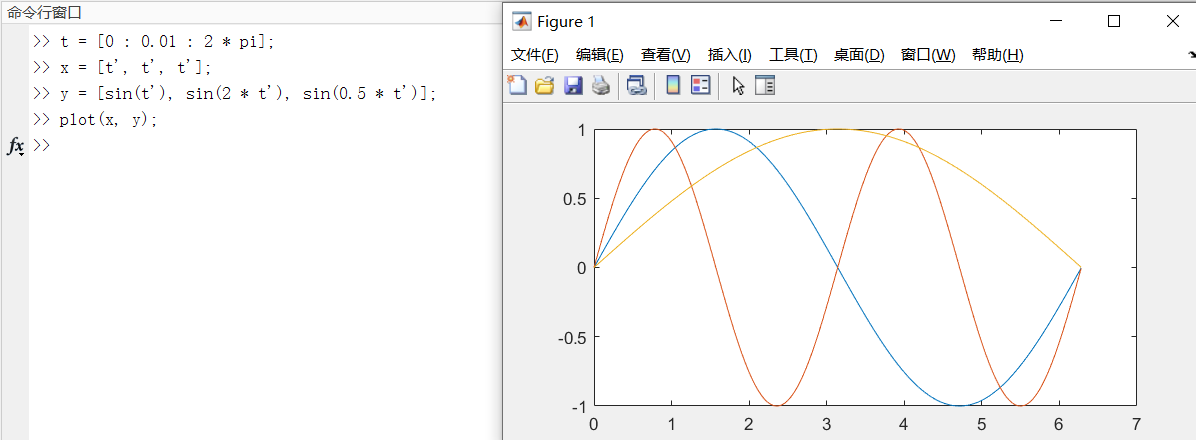
case3:plot(x,y),x、y为向量和矩阵
当 x 是向量,y 是矩阵时:
如下图:矩阵y的行数为3,列数为100;x的长度为100。情况为case1:x的长度 = 矩阵y的列数,则曲线的条数为矩阵y的行数。
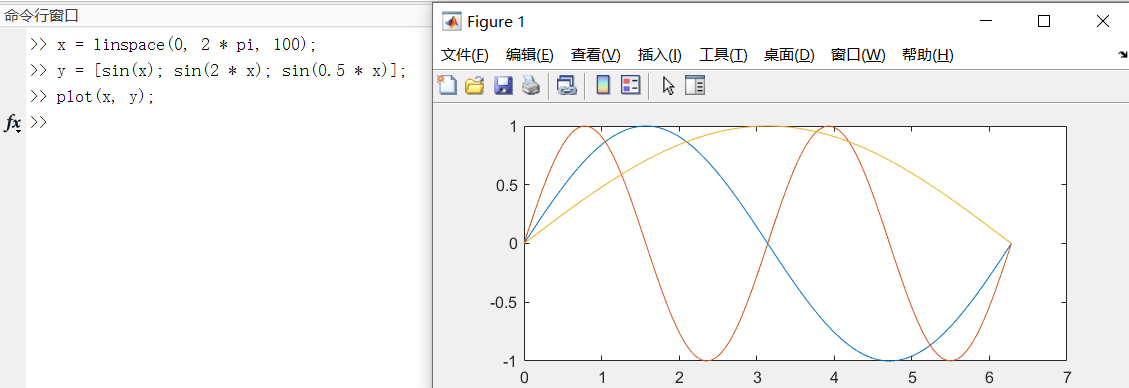
如下图:对
y进行转置操作,矩阵y的行数为100,列数为3;情况为case2:x的长度 = 矩阵y的行数,则曲线的条数为矩阵y的列数。
case4:plot(x,y),x、y为矩阵
当参数 x 为矩阵,参数 y 为矩阵,且为同型矩阵时:
以x、y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
如下图:采用这种方式绘制之前相同的图形
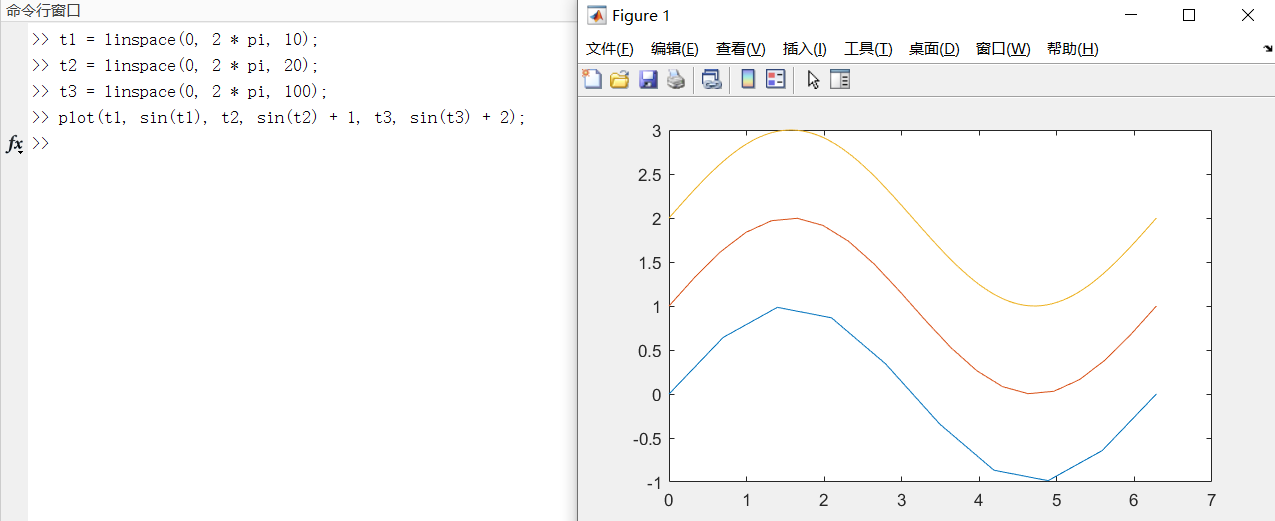
case5:绘制不同长度的曲线
plot(x1, y1, x2, y2, ... , xn, yn);
每一对向量对构成一组数据点的横纵坐标,绘制出一条曲线。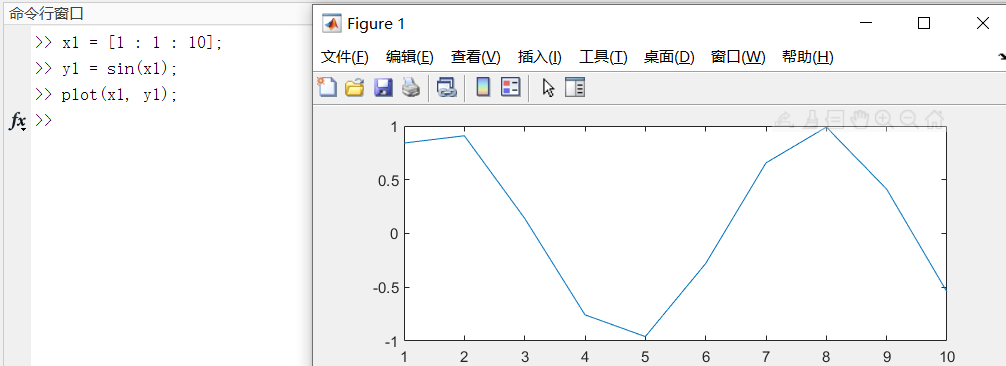
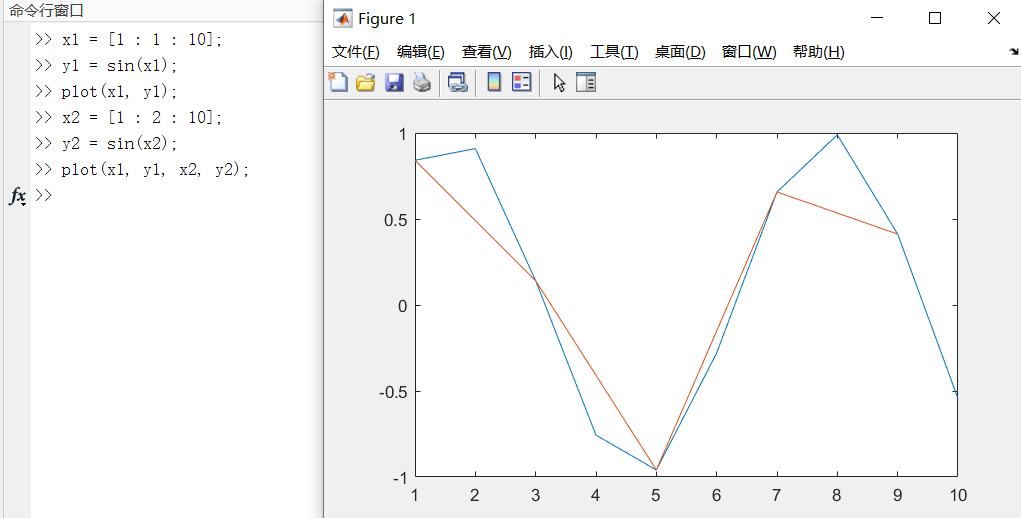
注意:在这里红色曲线在
x = 9时就结束了绘制,而蓝色曲线一直绘制到了x = 10
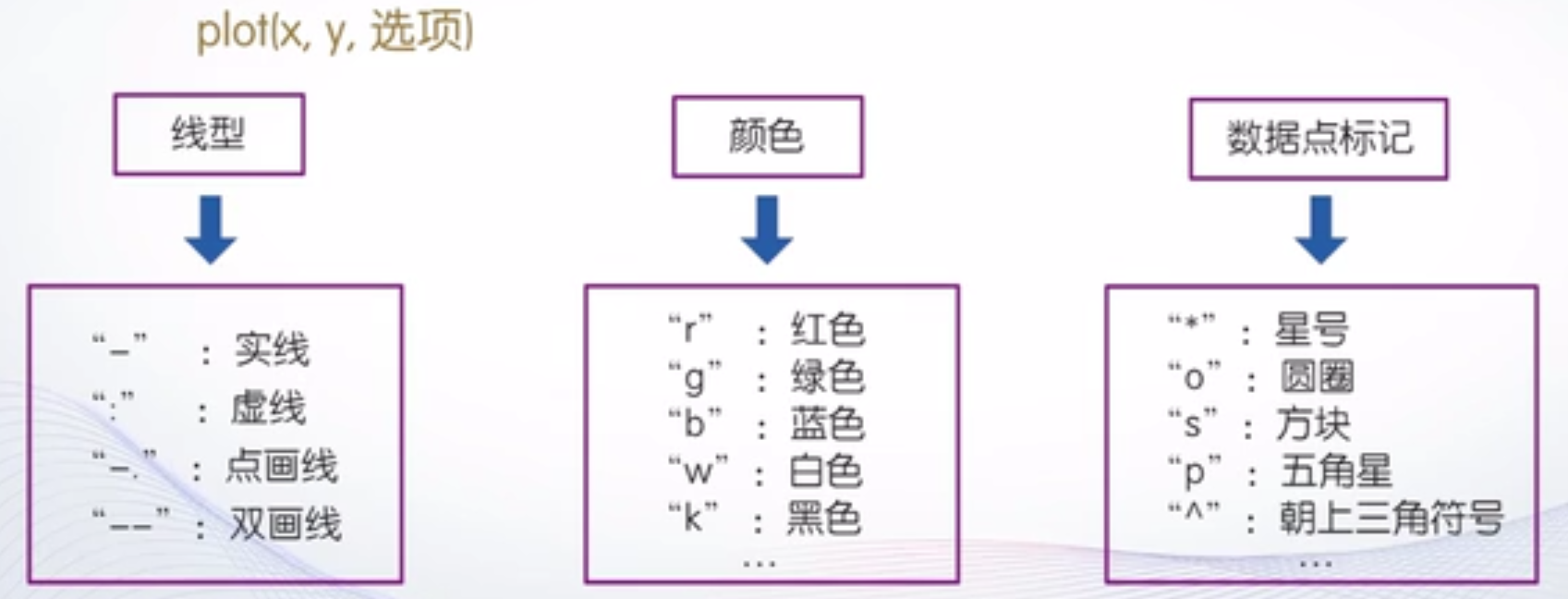
(2)plot(x, y)函数的样式:
(3)fplot函数:
在plot函数中x往往采取等间隔采样,这样导致某些曲线在某些区间无法准确的绘制出来。
使用fplot函数可以自适应的设置某些区间的采样间隔,可以更为准确的反应函数图像。
case1:fplot函数基本用法
调用格式:fplot(f, lims, 选项);
f:代表一个函数,通常采用函数句柄的形式
lims:为x轴的取值范围,用二元向量[xmin, xmax]描述,默认为[-5, 5]
选项与plot函数一致
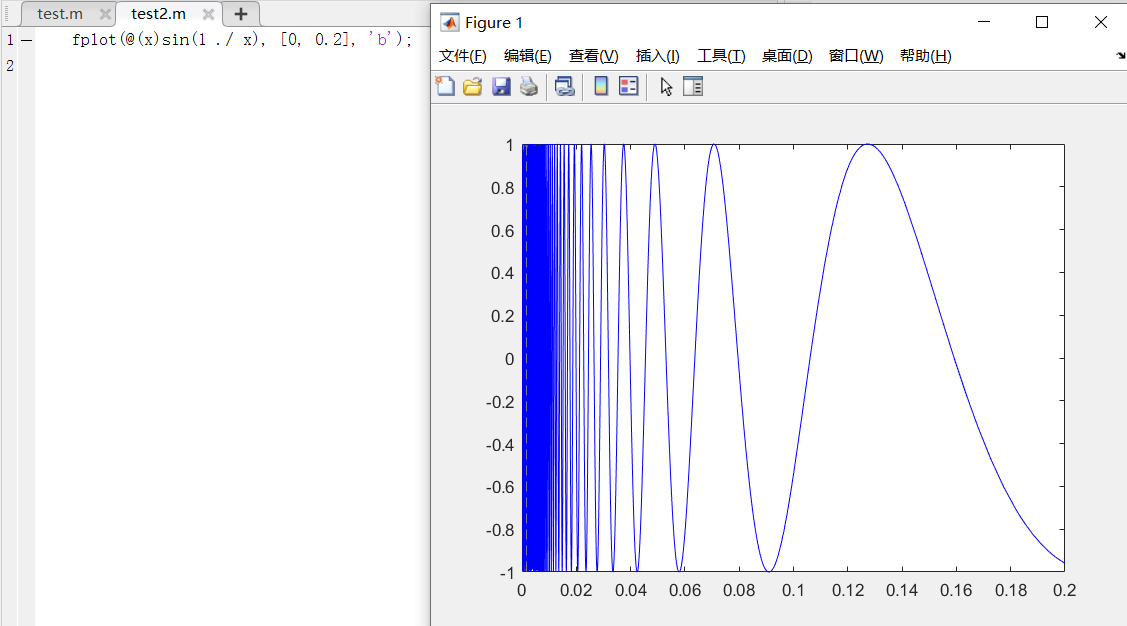
如图所示:fplot函数与plot函数绘制目标函数
f(x) = sin(1/x);图形对比如下所示:
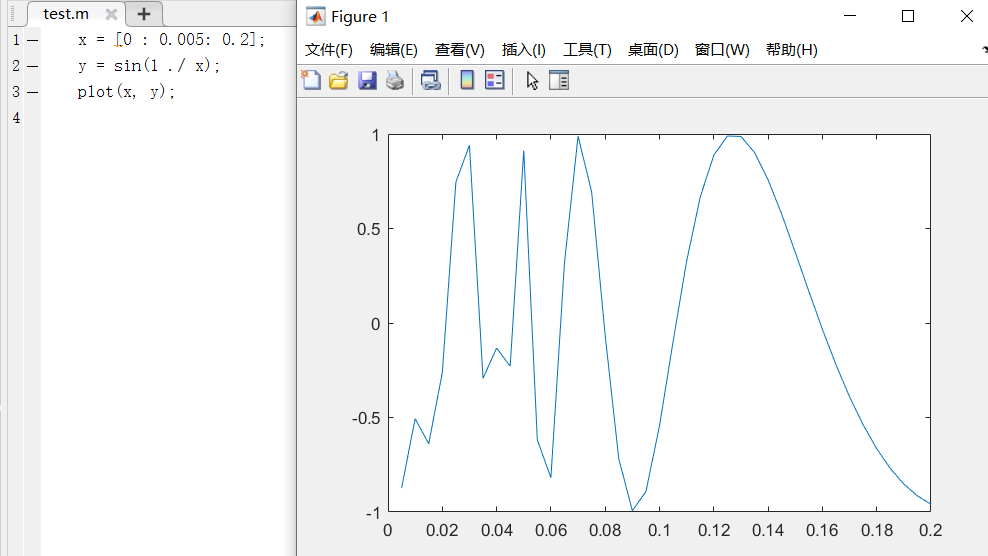
如果将fplot函数中的采样间隔缩小为原来的100分之一,得到的图形如下所示
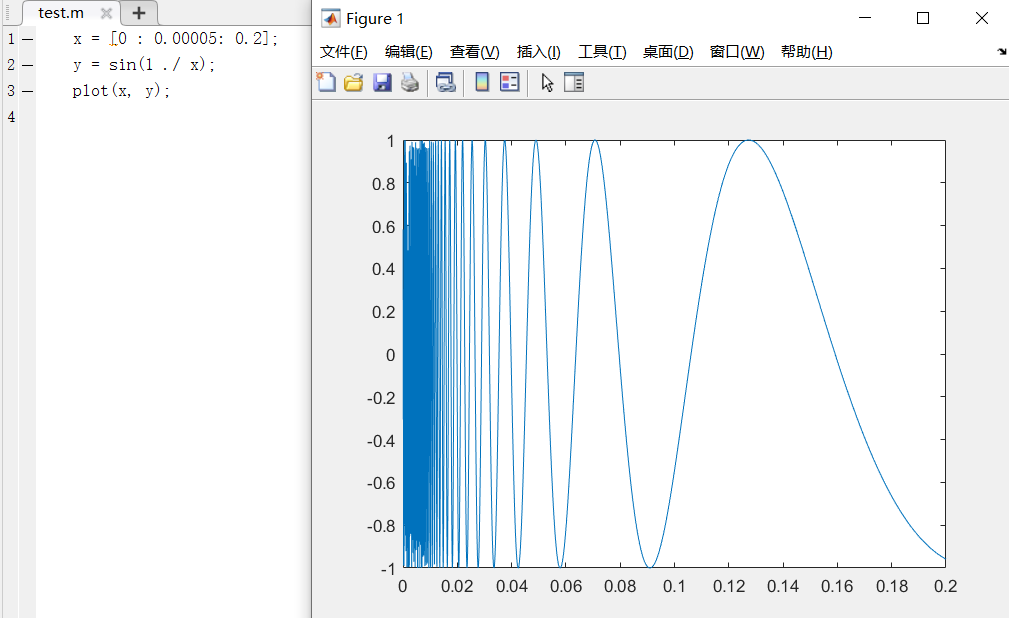
采用fplot函数自适应的设置区间的采样间隔,得到的绘图结果如下
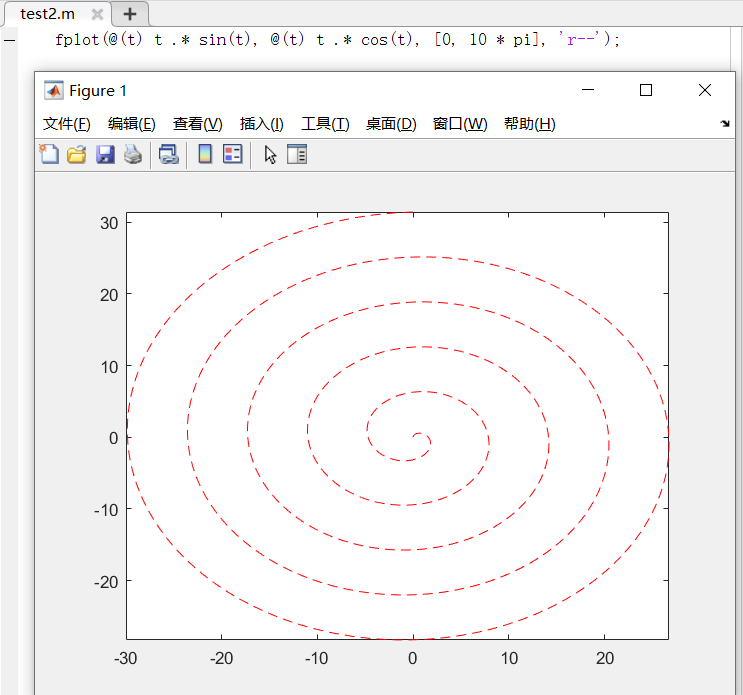
case2:输入双函数参数的用法
调用格式:fplot(funx, funy, tlims, 选项);
funx、funy:代表两个函数,通常采用函数句柄的形式
tlims:为参数函数funx、funy的自变量的取值范围,用二元向量[tmin, tmax]描述
2.绘制图形的辅助操作
(1)图形添加标注:

在各种标题和说明中还可以使用LaTex格式控制符显示数学公式
(2)坐标轴控制:
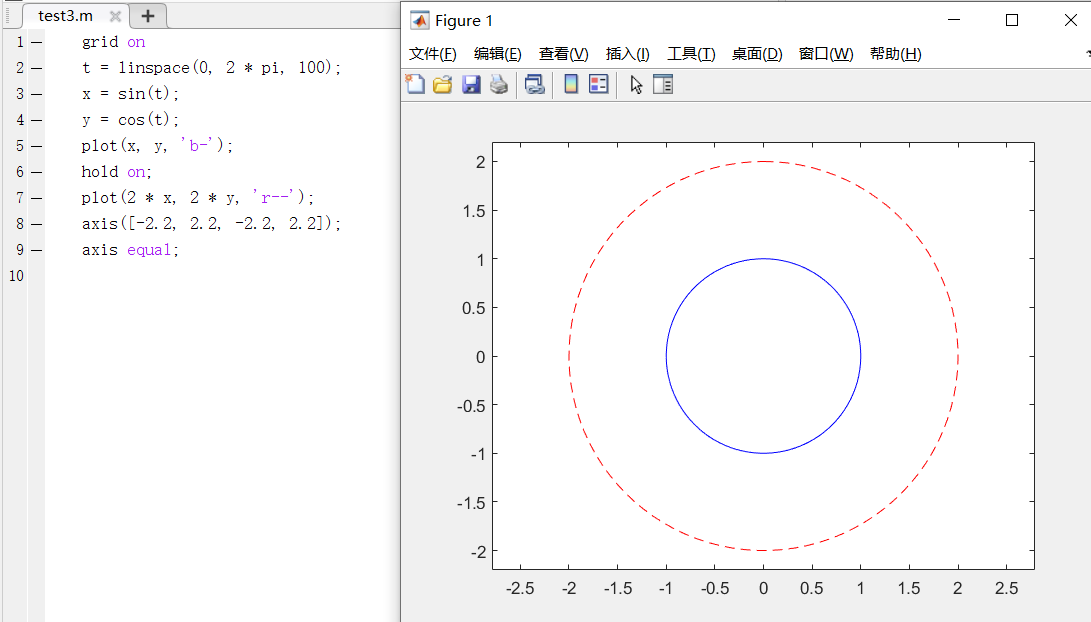
(3)图形保留:
一般情况下,绘图命令每执行一次绘图界面就会被刷新一次。若希望在已经存在的图形上继续叠加新的图形,可使用图形保持命令。
例:使用图形保留功能绘制两个同心圆,并更改坐标轴的原点为圆心、添加绘图网格
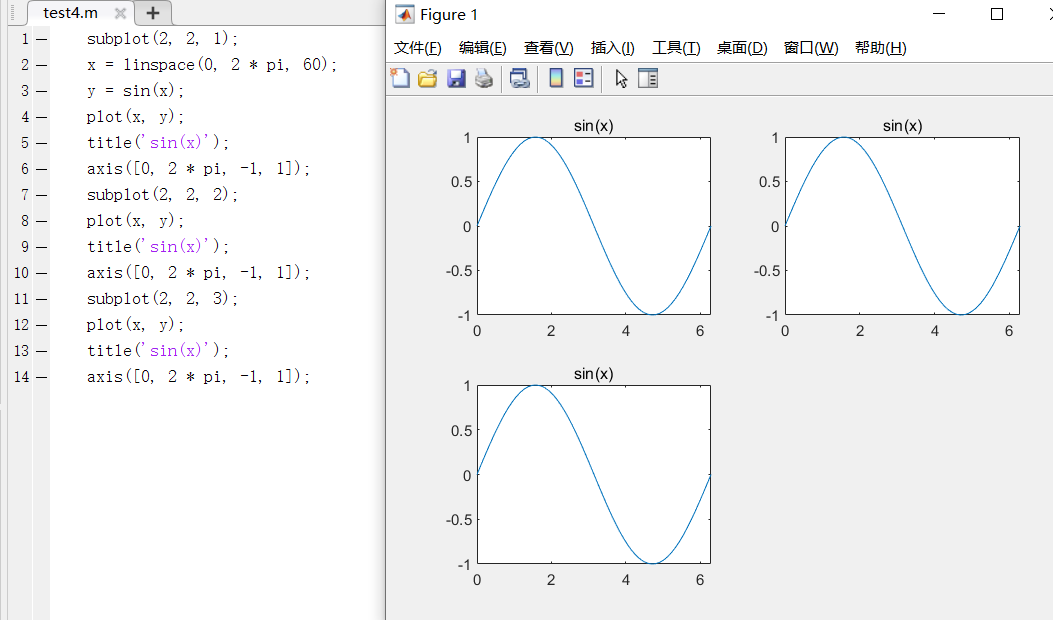
(4)图形窗口的分割:
若需要在一个窗口內绘制若干个独立的图形,便需要对图形窗口进行分割。
同一图形窗口中不同坐标系下的图形称为子图,matlab中提供了subplot函数对其进行处理
3.其他二维图形的绘制
(1)特殊坐标系下的二维曲线:
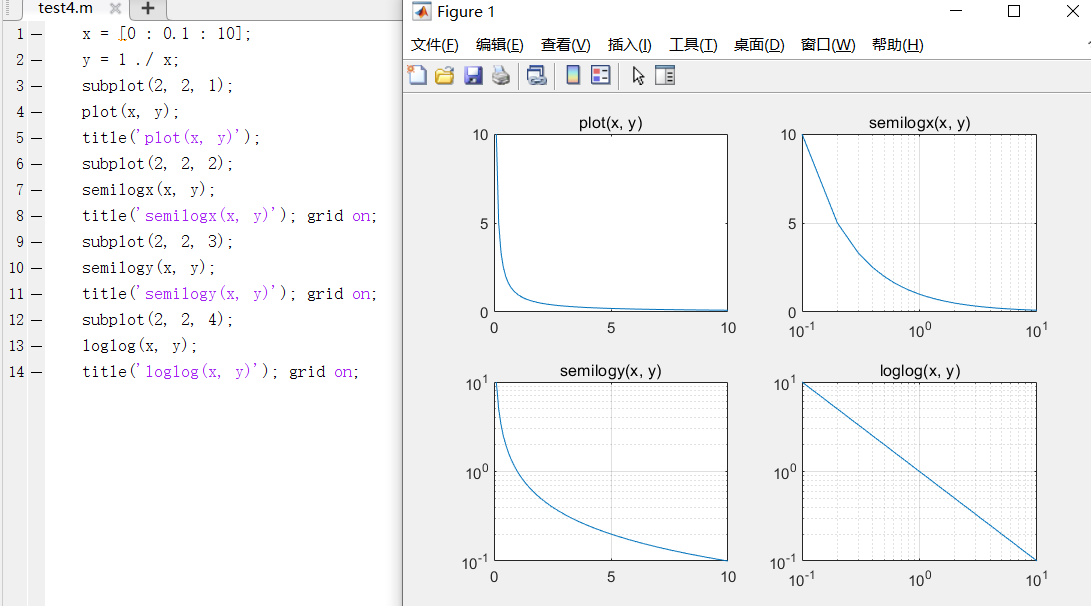
case1:对数坐标绘图

图例:在四种坐标图下绘制
f(x) = 1 / x的图形,包括logx、logy、loglog
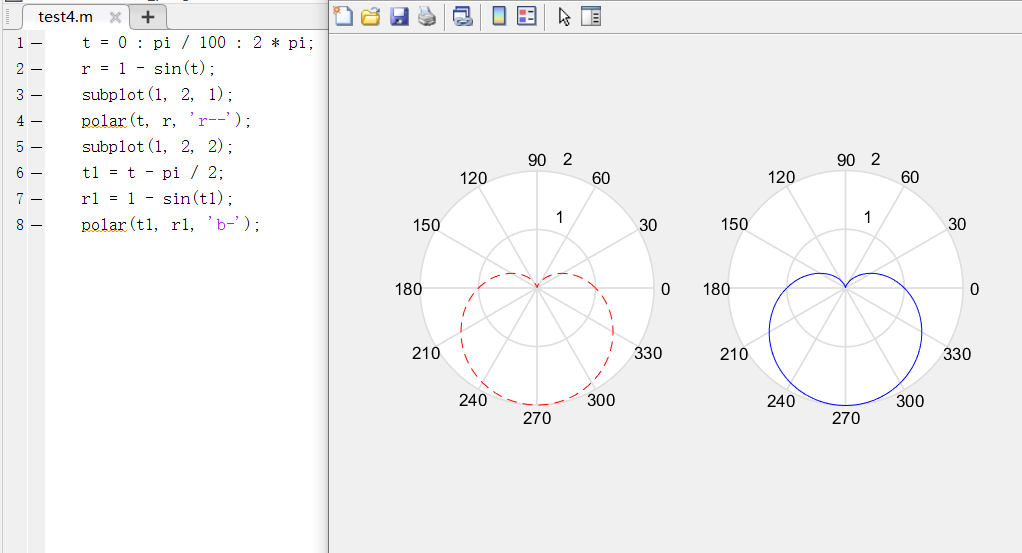
case2:极坐标绘图

图例:在极坐标图下,绘制心型曲线图
(2)统计图绘制:
case1:条形图

参数style中包括
grouped簇装分组和stacked堆积分组两种选项
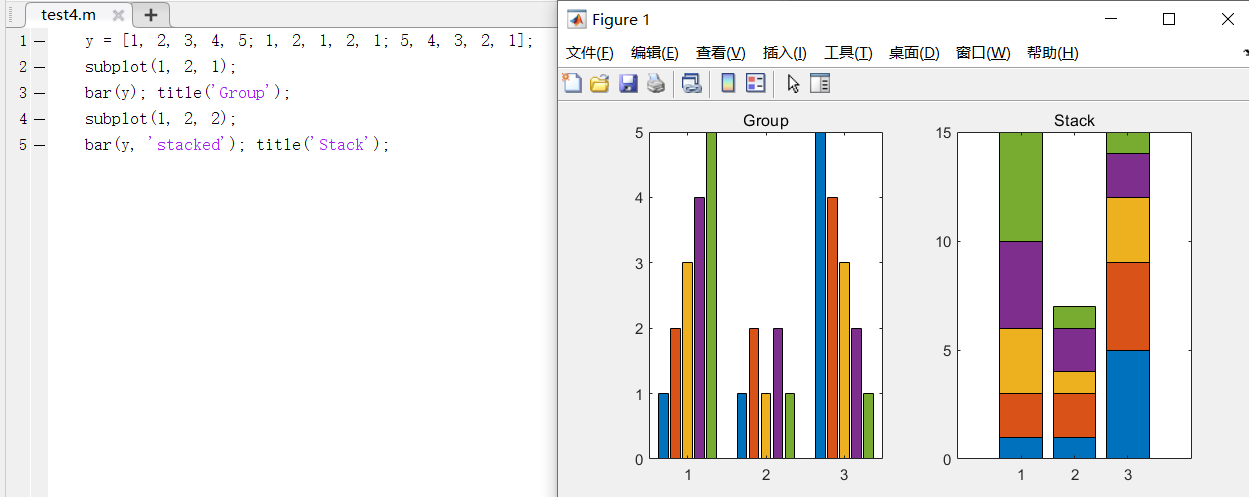
更多命令的使用详见help bar文档
case2:直方图

如果参数x没有指定,则默认划分为10个区间。图例为服从高斯分布的直方图
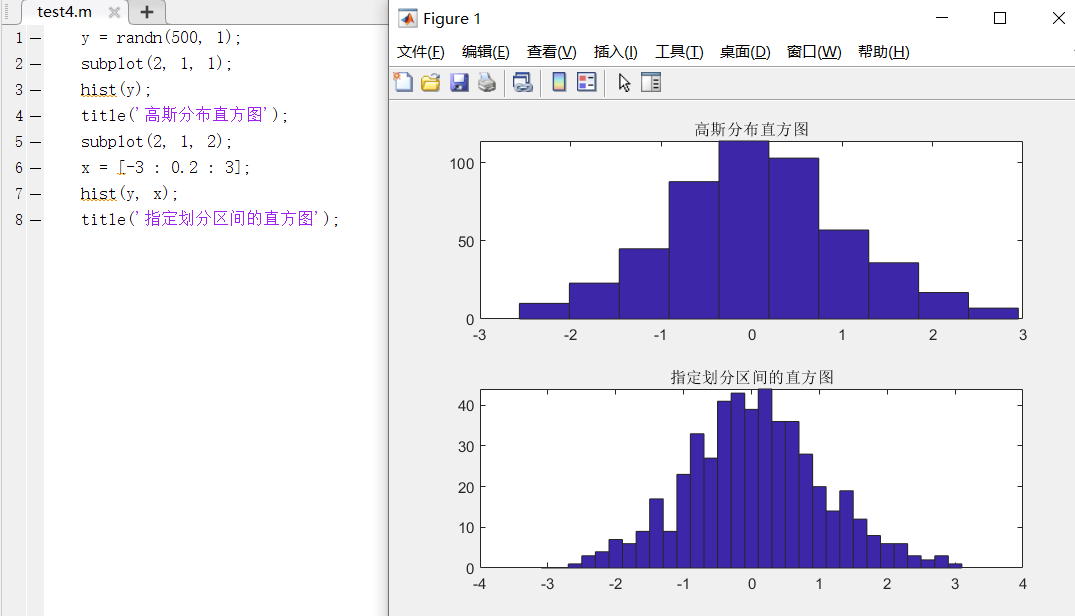

如果参数x没有指定,则默认划分为20个区间。图例为服从高斯分布的直方图在极坐标下的表现
case3:饼图

注意:
explode是与x同等大小的向量,省略explode时饼图是一个整体,图例为不及格人数饼图显示,不及格part需突出显示

注意:最后的
legend两个参数location、eastoutside如果不指定,图例将会显示在图形内部并遮挡一部分显示
case4:散点图
(3)矢量绘制:
3.三维曲线
(1)plot3函数:
case1:plot3(x,y,z)
其中x、y、z分别用于存储 x、y、z 坐标的数据,通常 x、y、z 为长度相等的向量。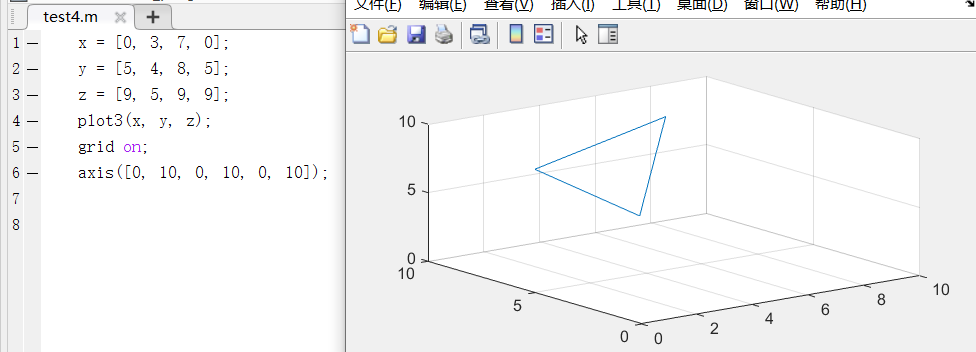
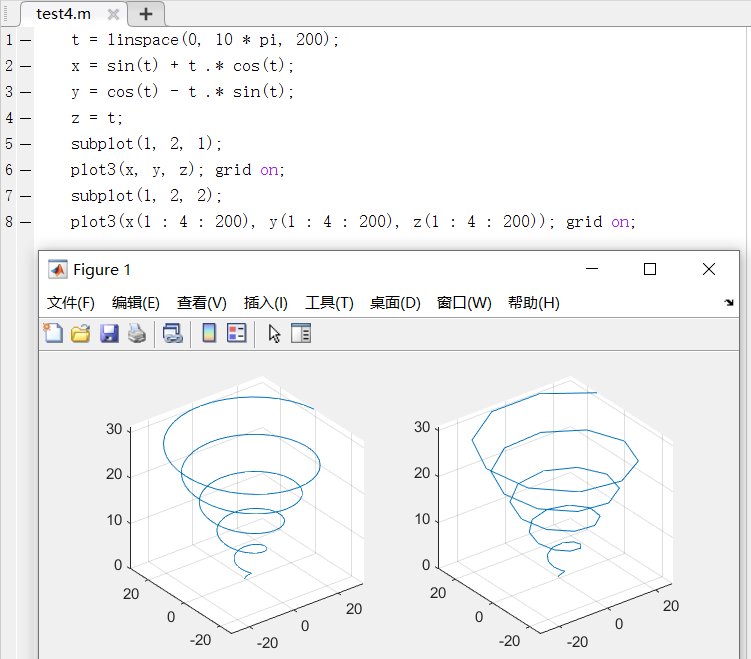
以下图例为使用
plot3函数绘制螺旋线函数图形
case2:plot3(x,y,z)函数参数变化
与
plot()函数类似的,plot3()函数根据参数变化也分为很多情况,具体可通过help plot3查阅说明手册
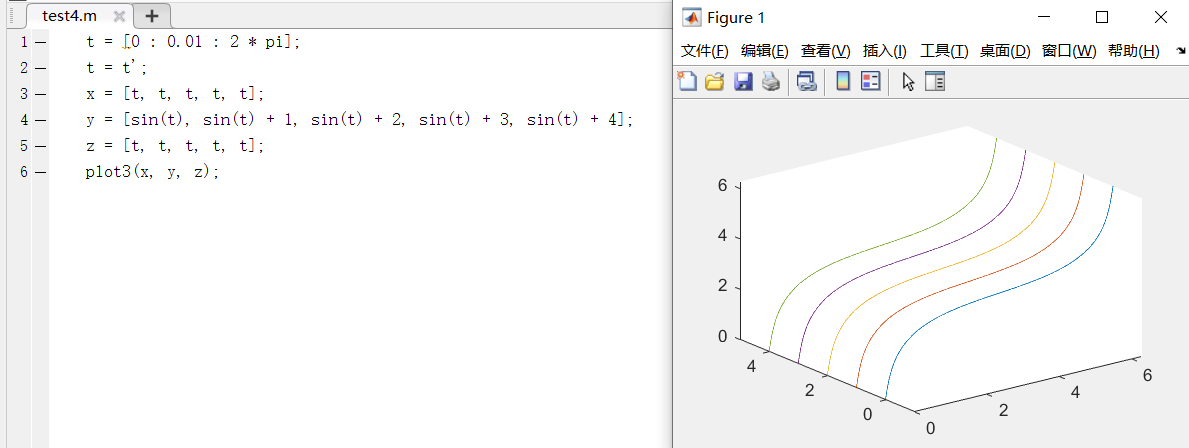
以下图例为在空间中不同位置绘制出5条正弦曲线
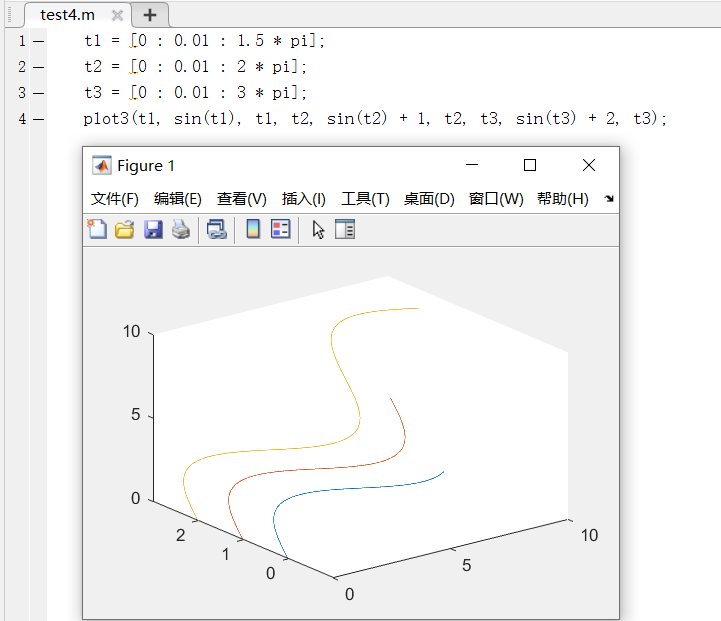
case3:绘制不同长度的曲线
plot(x1, y1, z1, x2, y2, z2 ... , xn, yn, zn);
与plot函数类似,每一对x、y、z向量构成一组数据点的坐标,绘制出一条曲线。
以下图例为绘制3条不同长度的正弦曲线,可以发现终止值不同决定了曲线长度的不同
(2)fplot3函数:
case1:fplot3函数基本用法
调用格式:fplot3(funx, funy, funz, tlims);
funx、funy、funz:代表定义曲线x、y、z坐标的函数,通常采用函数句柄的形式
tlims:为参数函数参数自变量的取值范围,用二元向量[tmin, tmax]描述,默认为[-5, 5];

4.三维曲面
(1)平面网格数据的生成:
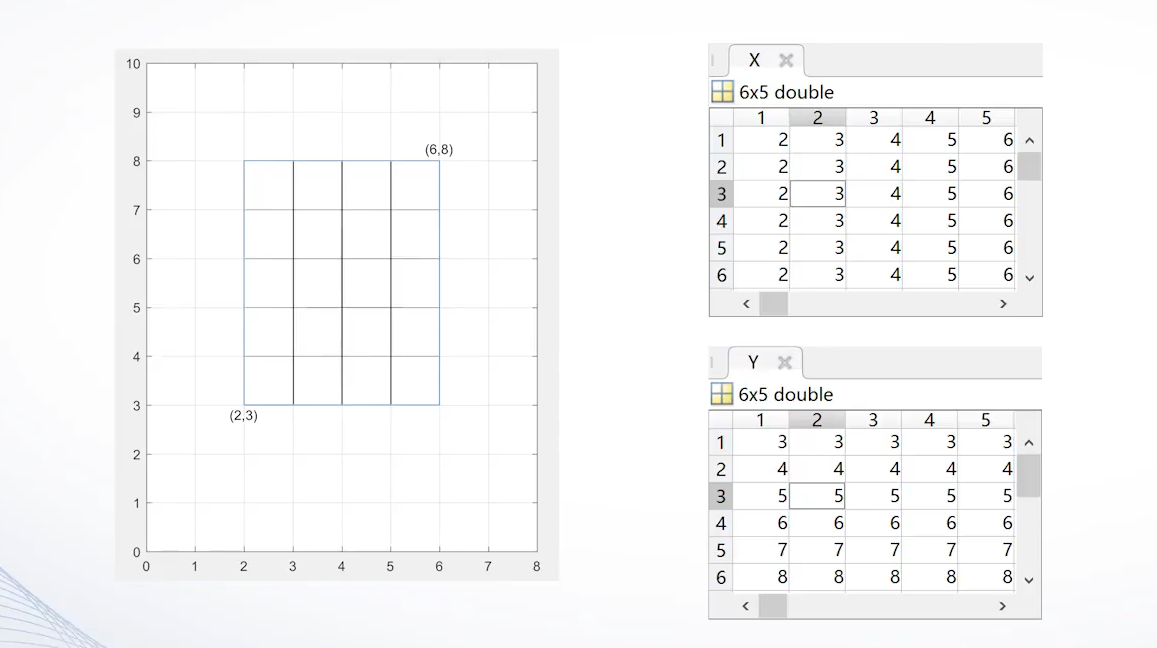
网格数据的定义如下图所示:
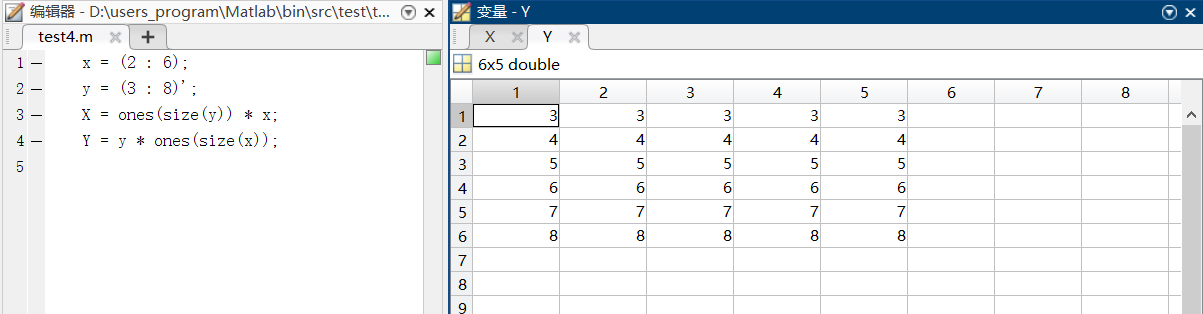
case1:利用矩阵运算生成网格数据
根据线性代数的矩阵运算知识,通过简单的观察和矩阵运算即可得到网格数据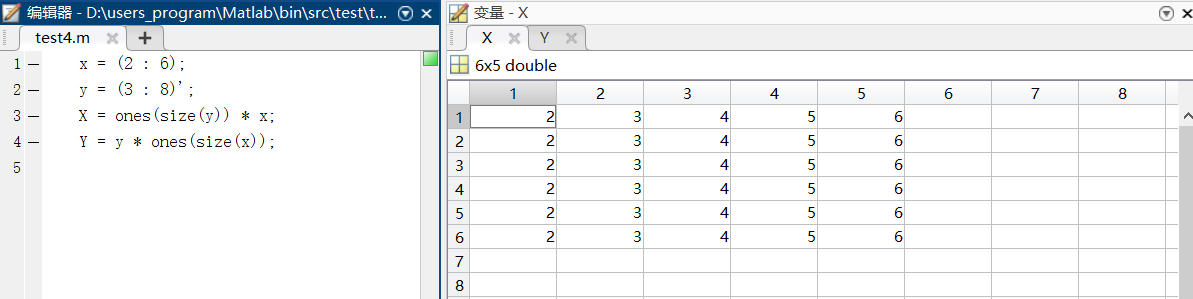
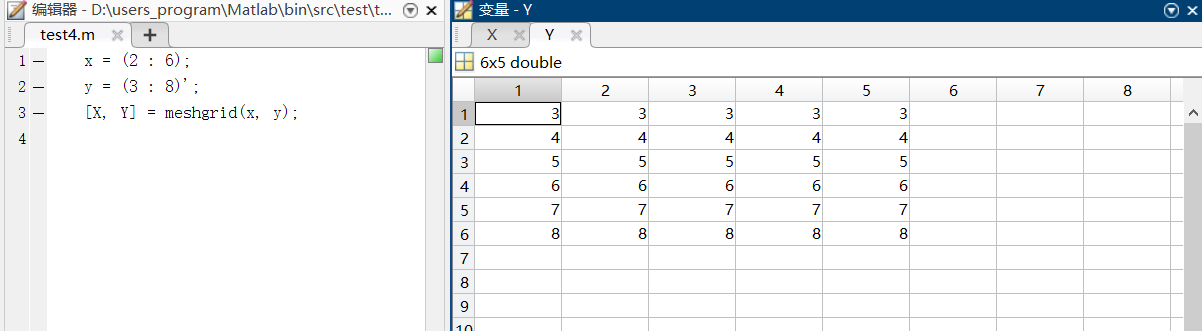
case2:利用meshgrid函数生成网格数据
调用格式:[X, Y] = meshgrid(x, y);
其中参数x、y为向量,存储网格点坐标数据的X、Y为矩阵
例如上例中网格数据的自动生成如下,观察网格生成的数据可发现meshgrid生成网格数据的特点。
(2)绘制三维曲面的mesh函数和surf函数:
case1:mesh(x, y, z, c);、surf(x, y, z, c);
其中,x、y 是网格坐标矩阵,z 是网格点上的高度矩阵,c 用于指定在不同高度下的曲面颜色。
当参数c省略时,默认为c等于z的值,即曲线颜色的设定是正比于图形的高度的。

| 三维绘图函数 | 图像特点 |
|---|---|
mesh(x, y, z) |
绘制的图形线条具有颜色,线条间的补面没有颜色 |
surf(x, y, z) |
绘制的图像线条颜色为黑色,线条间的补面有颜色,且颜色与z轴变化相关 |
plot3(x, y, z) |
绘制图形由三维曲线组合而成 |
case2:mesh(z,c);、surf(z,c);
当参数 x 、 y 省略时,z 矩阵的第2维下标当作 x 轴坐标,z矩阵的第1维下标当作 y 轴坐标。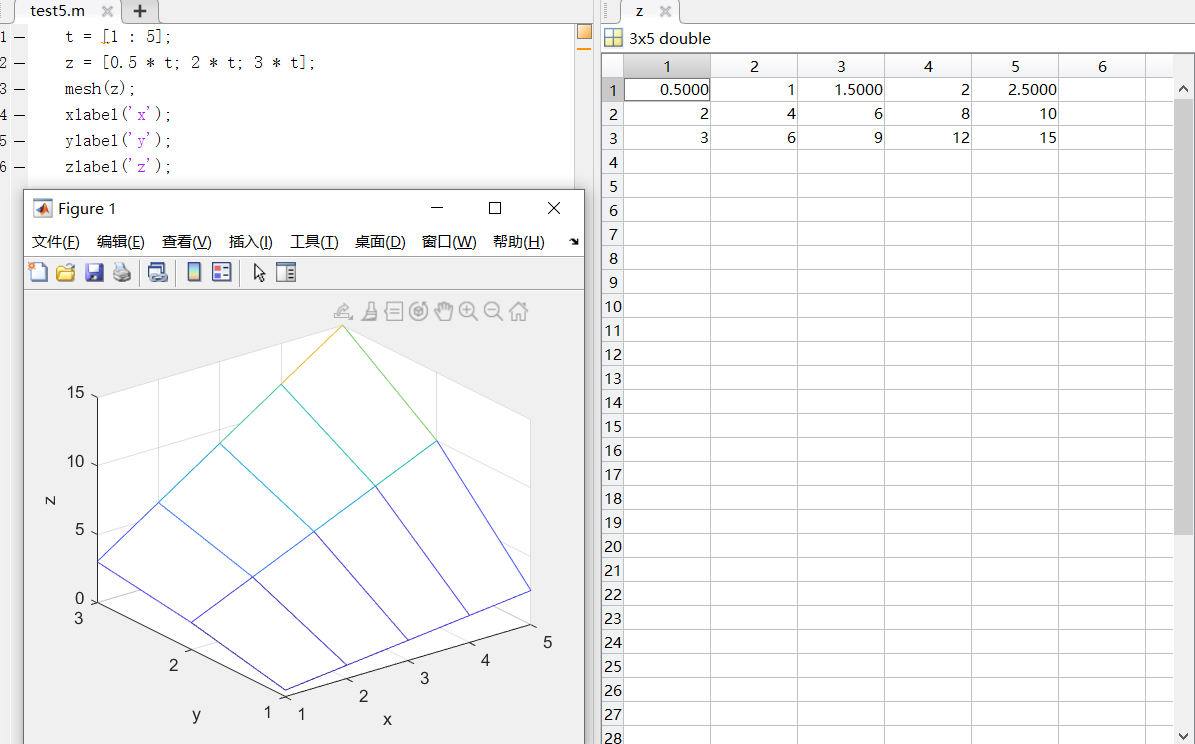
分析:上图例中,z矩阵的第2维下标为列坐标(6列),第1位坐标为行坐标(3行),图像各点高度z值为矩阵中对应的元素值
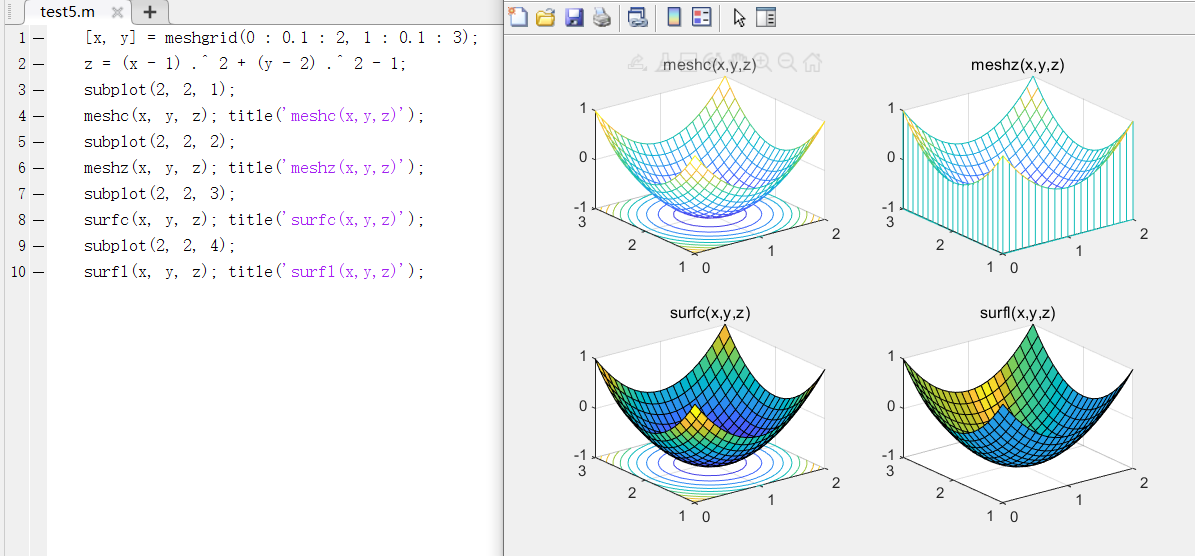
case3:meshc、meshz、surfc、surfl函数
(3)绘制特殊的标准三维曲面函数:
(4)绘制多方程三维曲面fsurf函数和fmesh函数:
如果图形由三个参数方程定义,并且参数方程有两个自变量,此时可以使用matlab提供的fsurf和fmesh函数绘制三维曲面。
fsurf、fmesh函数与fplot双参数调用类似,可借鉴
调用格式:fsurf(funx, funy, funz, uvlims);、fmesh(funx, funy, funz, uvlims);
funx、funy、funz:代表定义曲面x、y、z坐标的函数,通常采用函数句柄的形式
uvlims:为参数函数自变量的取值范围,用4元向量[umin, umax, vmin,vmax]描述,默认为[-5, 5, -5, 5];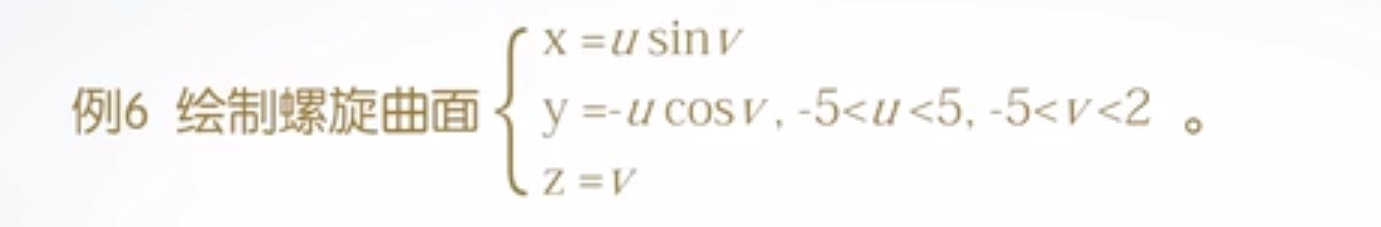

5.图形修饰处理
(1)视点处理
(2)色彩处理
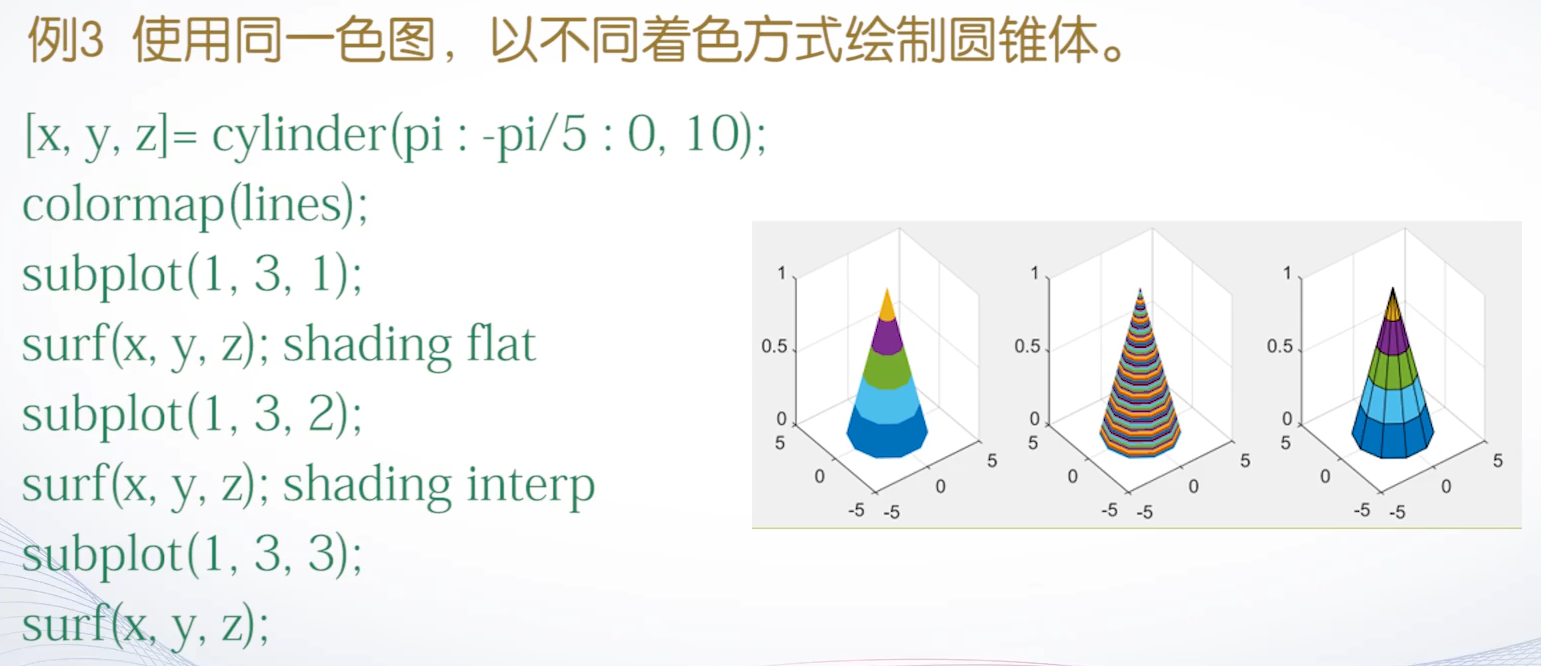
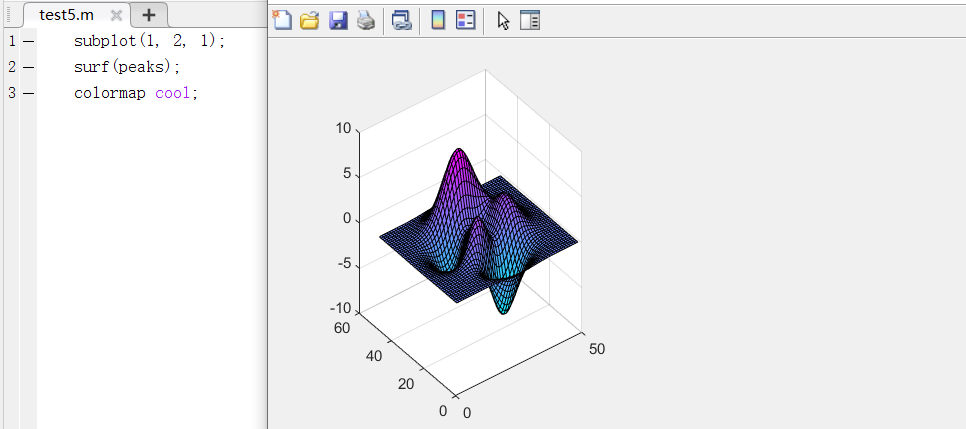
case1:三维曲面着色颜色colormap
调用方式:colormap cmapname;、colormap(cmap);指定当前曲面使用色图
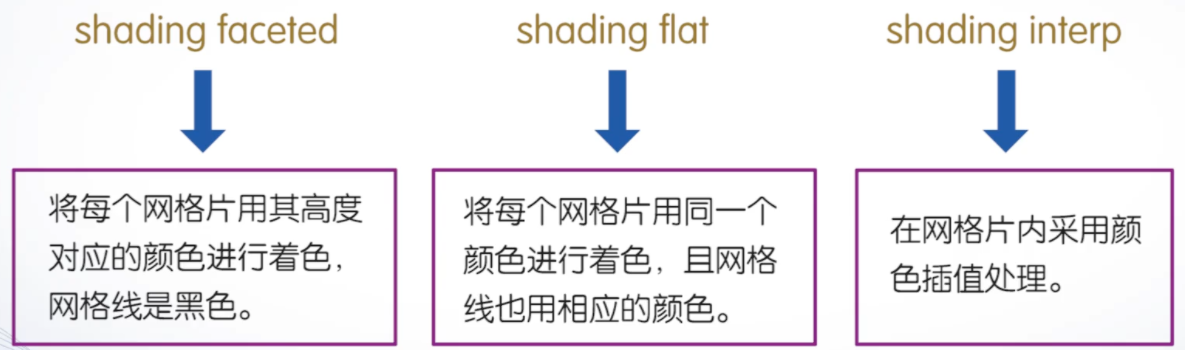
case2:三维曲面着色方式shadding
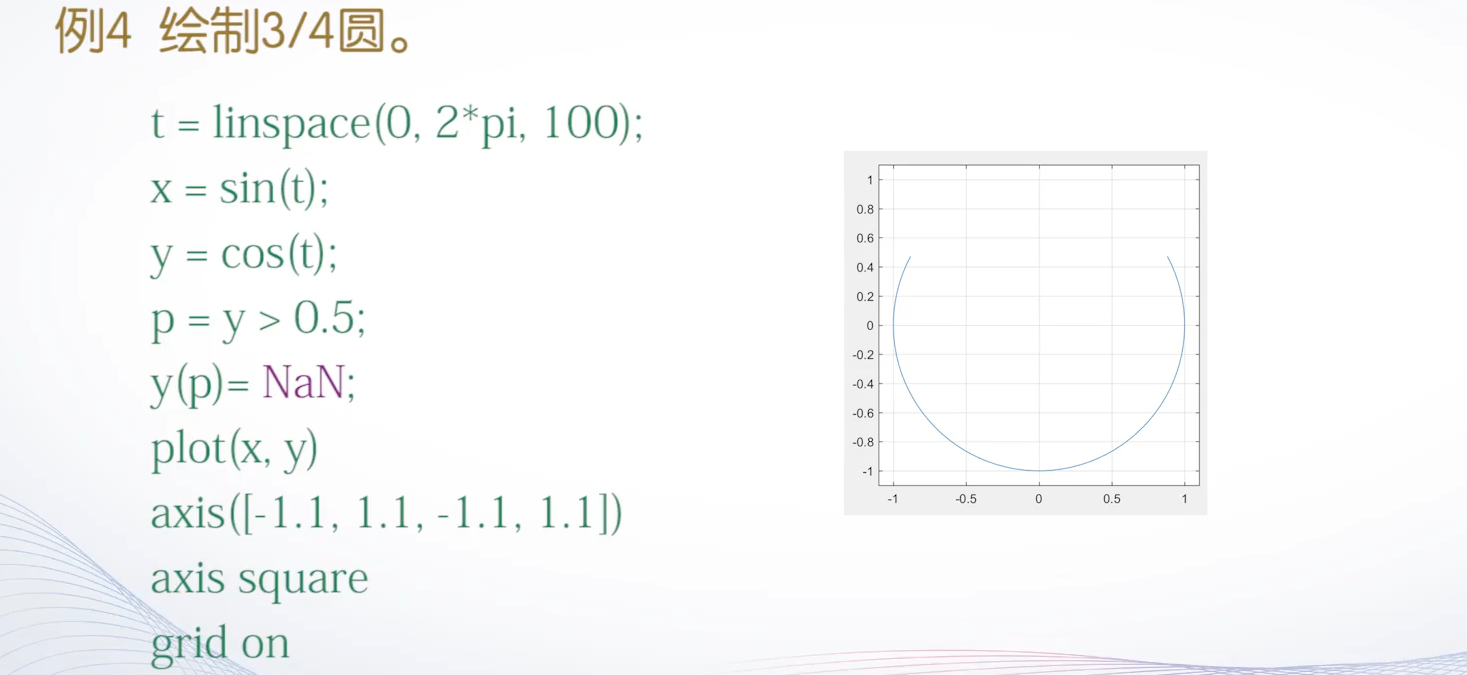
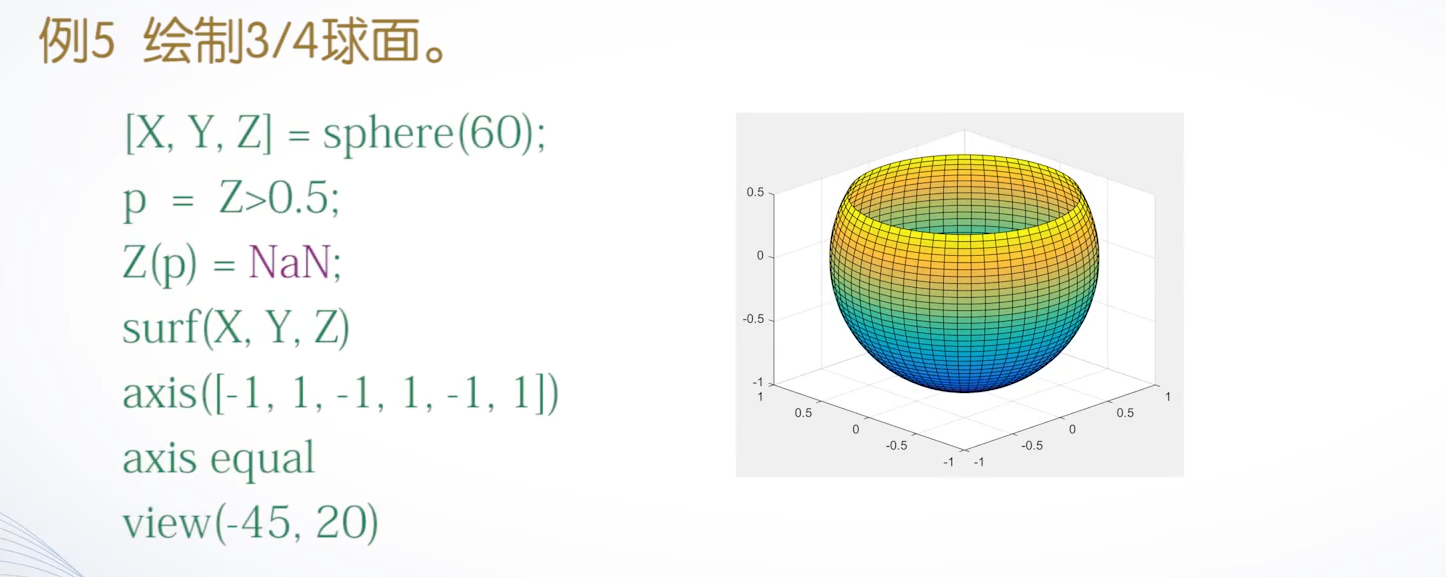
(3)剪裁处理
在图形中将需要裁剪的函数值设置为NaN,这样绘制图形时函数值为NaN的部分将不显示出来,从而达到对图形进行裁剪的目的。