一、模型与数学模型的基本概念
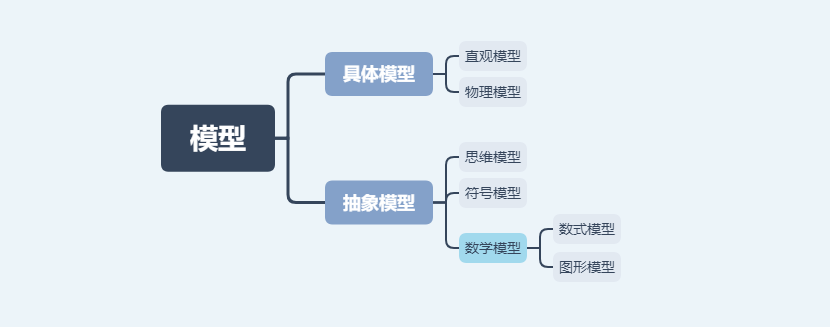
1.模型的分类:
2.数学模型的分类:
方式1:按所用的数学知识:
初等模型、几何模型、微积分模型、微分方程模型、图论模型、概率统计模型、规划论模型等
方式2:按所解决的问题领域分类:
物理模型:自然科学领域内的问题
非物理模型:经济模型、交通模型、人口模型、生态模型、环境模型、医学模型、社会学模型、
方式3:按建模目的分类:
描述模型、分析模型、预报模型、优化模型、决策模型、控制模型
方式4:按模型的表现特性分类:
确定模型、随机模型、静态模型、动态模型、离散模型、连续模型
二、建模的一般步骤
模型假设:针对问题特点和建模目的做出合理的、简化的假设(合理与简化之间作出折中)
建立模型:用数学的语言、符号描述问题(尽量采用简单的数学工具)
1.问题表述:
问题表述(问题重述)是根据建模的目的和信息将实际问题翻译成自己理解的数学问题
2.模型求解:
选择适当的数学方法(MATLAB或者是计算机语言)求得数学模型的解答
3.解释对象:
在模型求解出结果后,对结果进行分析以及其中蕴含的浅/深层信息
4.验证问题:
用现实对象的信息检验得到的答案
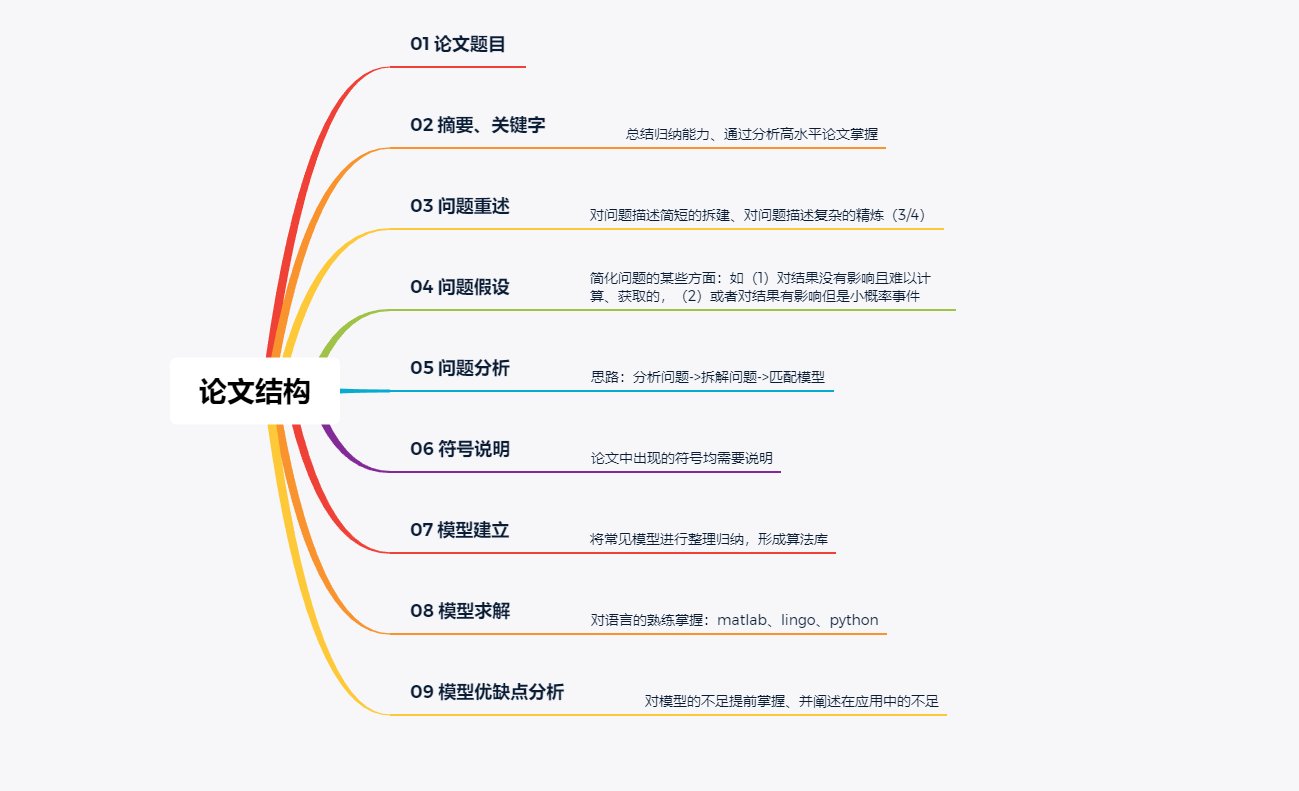
三、数模论文的结构
四、关于团队协作与分工
1.团队分工:
(1)建模分工:
建模在竞赛中负责建立模型的整体脉络,需要多接触数学类的知识如运筹学、模糊数学、数据分析,以便在建模时能够匹配相应的模型。
建模人员必须要掌握的模型:
评价类:层次分析法、模糊综合评价、TOPSIS、神经网络
预测类:回归预测、时间序列预测、神经网络预测、马尔科夫预测
优化类:线性和非线性规划、整数规划、0-1规划、多目标和智能优化
数据处理:插值拟合、归一化、主成分分析
聚类分析:k-means聚类、SVM聚类分析、随机深林和决策树
相关性分析:灰色关联分析、皮尔逊系数
图与网络:最短路径、旅行商(TSP问题)、最小生成树、网络最大流
其他算法:微分方程、元胞自动机、蒙特卡洛算法
(2)编程分工:
负责为建立的数学模型进行编程,需要掌握使用的软件有MATLAB、LINGO和SPASS等。
必须能够熟练掌握各种常用建模算法的编程实现,并事先将其分门别类的储存好
对于常见的选择、循环等语句结构和微分方程组的求解都能熟练掌握
对于数据可视化、绘图等也能熟练掌握
(3)论文编写:
使用学术型语言写出建模论文,能够清晰的表达出模型建立的过程,需要较强的语言能力。
2.团队协作:
在选题刚公布时,编程和写作的队员是没有任何工作的,所有人应该集中起来研究赛题,确定选题后分析思路。
建立模型工作开始后,分工开始安排,建模人员搭建何种模型,编程人员需要提前编写模型实现过程,写作人员针对模型逻辑开始撰写问题分析和模型建立等内容。