一、MATLAB基础知识
1.matlab矩阵表示
(1)普通矩阵的建立:
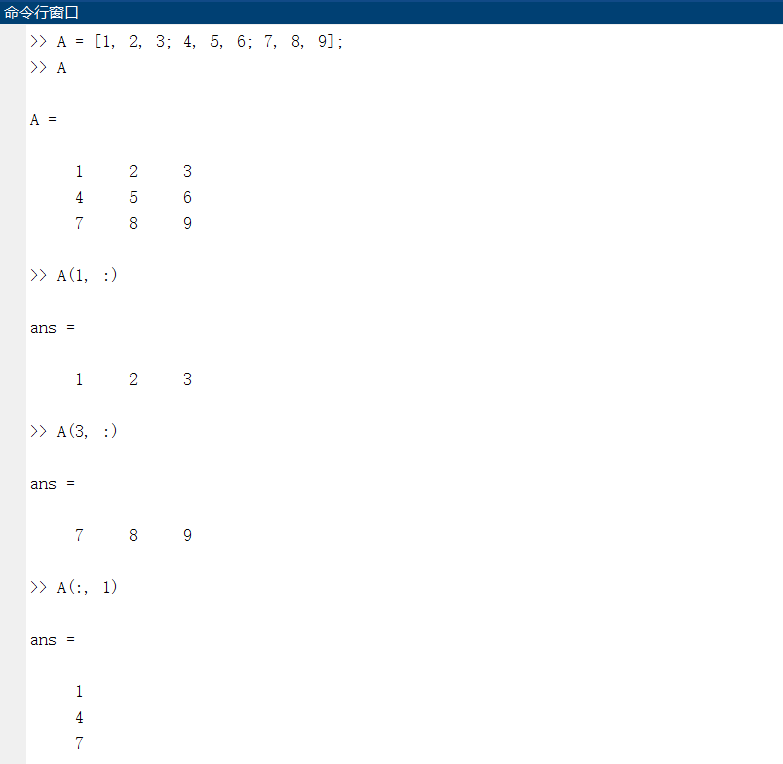
case1:直接输入法建立矩阵
将矩阵的元素用中括号括起来,按照矩阵的顺序输入各元素。同一行的各元素之间用逗号或空格分割,不同行之
间的元素用分号分割。
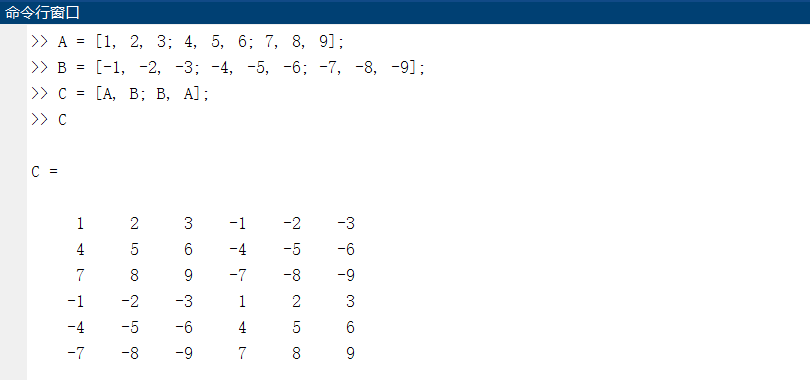
case2:利用已有矩阵建立更大矩阵
case3:利用实部、虚部矩阵构成复数矩阵
case4:冒号表达式
格式:e1:e2:e3,(初始值:步长:终止值)
若步长省略则默认为1,二维矩阵若省略初始和终止值则表示矩阵的一整行 or 列
case5:linspace函数产生行向量
格式:linspace(a, b, n),(a:第一个元素, b:最后一个元素, n:元素总数)
若元素总数n省略,则自动默认产生100个元素

(2)单元矩阵的建立:
建立单元矩阵和一般普通矩阵相似,直接输入法建立即可,只是单元矩阵元素用大括号括起来。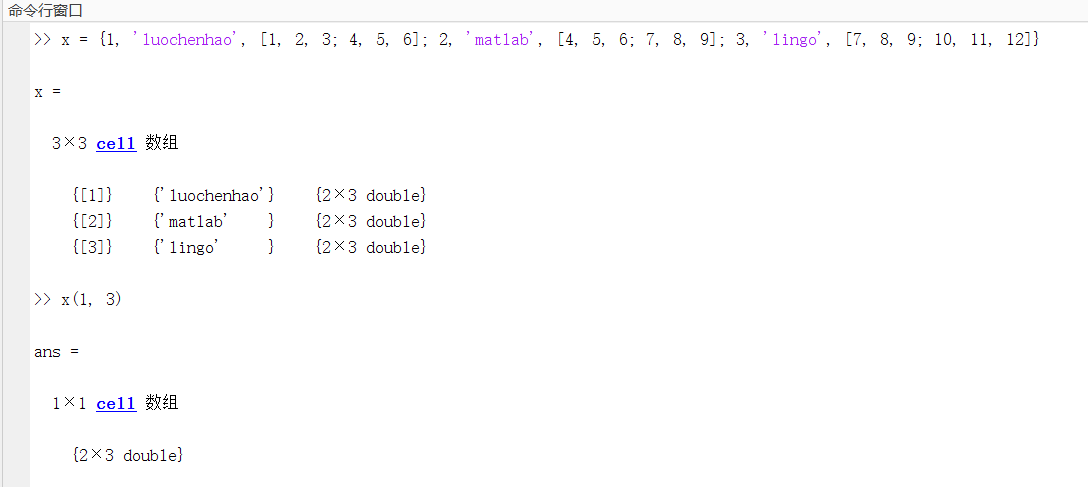

2.matlab矩阵元素的引用
(1)通过下标引用矩阵元素:

(2)通过序号引用矩阵元素:
在matlab中,矩阵的元素是按列存储的即首先存储第一列元素、第二列…一直到最后一列。
矩阵元素的序号就是矩阵元素在内存中的排列顺序。

(3)矩阵元素下标与序号的相互转换:
通过观察发现一个矩阵 Ai,j 中的元素的下标i、j与元素对应的序号index的关系为:index = (j - 1) * (m + 1);
matlab中也提供了sub2ind与ind2sub函数实现下标与序号之间的转换:
case1:矩阵下标转序号sub2ind
sub2ind函数将矩阵中指定元素的行、列下标转换成存储的序号,调用格式为:D = sub2ind(S, I, J);
D:矩阵元素的序号(转换结果)
S:行数和列数组成的向量[i, j]
I:转换矩阵元素的行下标i
J:转换矩阵元素的列下标j

注意:如果sub2ind函数中参数
I、J也为矩阵(此时必须保证I、J行列数相同,与D),表示要将矩阵中的多个元素下标转换为序号
case2:矩阵序号转下标ind2sub
ind2sub函数将矩阵中指定元素存储的序号转换成对应的行、列下标,调用格式为:[I, J] = ind2sub(S, D);
I:序号对应矩阵元素的行下标i
J:序号对应矩阵元素的列下标j
S:需要转换矩阵的行数和列数组成的向量[i, j]
D:元素存储的序号
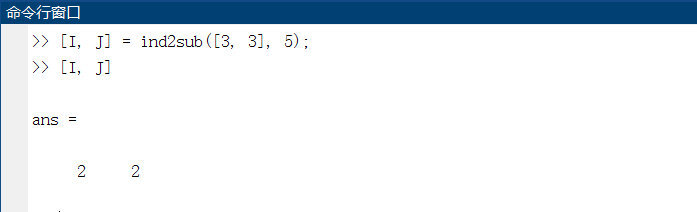
注意:如果ind2sub函数中参数D为数组,则表示要将矩阵中的多个元素序号转换为下标
(4)利用冒号表达式引用矩阵元素:
利用冒号表达式引用矩阵元素如下:
| 矩阵引用 | 含义 |
|---|---|
A(i, :) |
引用矩阵A中的第i行全部元素 |
A(:, j) |
引用矩阵A中的第j列全部元素 |
A(i:i + m, k:k + m) |
引用矩阵A中在第i~ i + m行, k~ k + m列中的所有元素 |
A(i:i + m, :) |
引用矩阵A中在第i~ i + m行中的所有元素 |
(5)矩阵的其他操作:
case1:删除矩阵的元素:
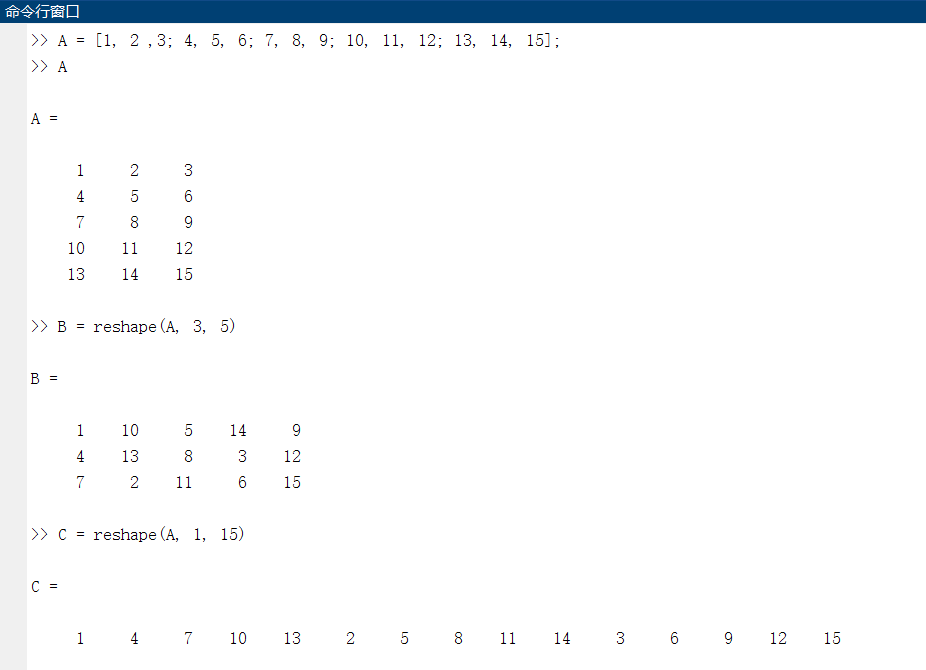
case2:强行改变矩阵形状:
这里的矩阵变换再次验证了,矩阵的元素是按列存储的
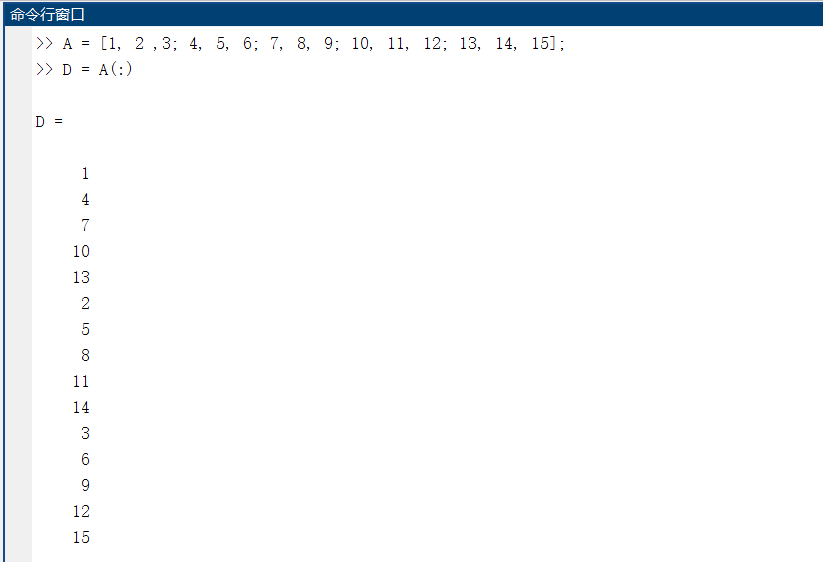
case3:特殊操作:A(:)列堆叠
3.matlab矩阵基本运算
(1)算术运算:
基本算术运算包括:加+、减-、乘*、右除/、左除\、乘方^,注意:matlab算术运算是在矩阵意义下进行的,满足矩阵运算规律
另注:乘方运算要求被运算矩阵为方阵,乘方数为标量
(2)点运算:
点运算包括:点乘方.*、点右除./、点左除.\、点乘方.^,点运算与基本运算不同在于点运算作用于两矩阵对应元素(故要求矩阵同型)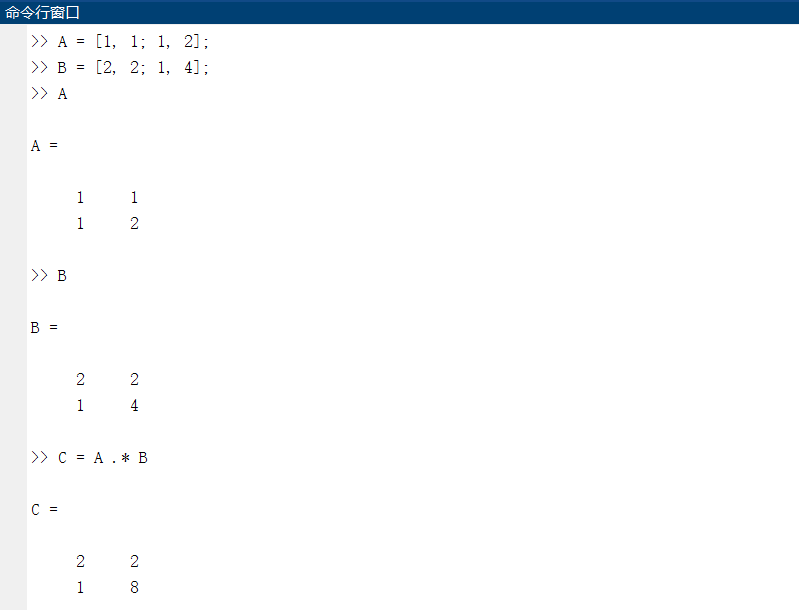
二、MATLAB矩阵处理
1.特殊矩阵:
(1)通用的特殊矩阵:
(2)专门学科的特殊矩阵:
| 特殊矩阵 | 生成代码 |
|---|---|
| 魔方阵 | magic(n) |
| 范德蒙矩阵 | vander(V) |
| 希尔伯特矩阵 | hilb(n) |
| 伴随矩阵 | compan(p) |
| 帕斯卡矩阵 | pascal(n) |
2.矩阵变换:
(1)对角阵:
(2)三角阵:
(3)矩阵的转置:
复数矩阵的转置与共轭转置结果是不同的,实数矩阵的转置与共轭转置结果是相同的
(4)矩阵的旋转:
(5)矩阵的翻转:
(6)矩阵求逆:
3.矩阵求值:
(1)矩阵的行列式值:
(2)矩阵的秩:
(3)矩阵的迹:
(4)矩阵的范数:
(5)矩阵的条件数:
4.矩阵的特征值与特征向量:
设A是n阶方阵,如果存在常数 λ 和 n维非零列向量 x ,使得等式 A·x = λ·x 成立,
5.稀疏矩阵:
稀疏矩阵存储方式为,只存储矩阵中非零元素的值及其位置,即行号和列号。
注意:采用稀疏储存方式时,矩阵元素的存储顺序并没有改变,也是按列顺序进行存储



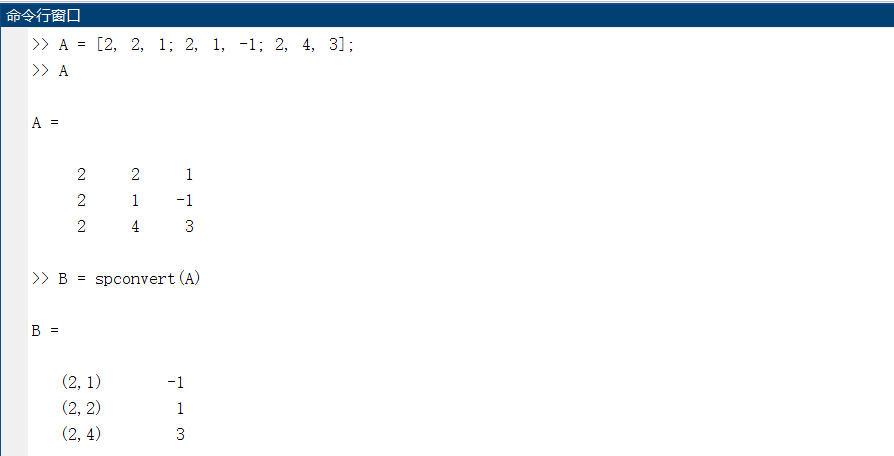
*描述的稀疏矩阵转化为稀疏存储矩阵:
- step1:稀疏矩阵的描述方法

- step2:稀疏矩阵存储的转化: