机器学习第一次编程作业:
分别生成线性可分数据集和非线性可分数据集,对每个数据集均采用PLA算法及Pocket算法进行分类。比较两种算法的各自优劣性。
1.生成数据集
import randomimport pandasfrom pandas import DataFramedata1=DataFrame(columns=['X','Y','label'])#数据集1data2=DataFrame(columns=['X','Y','label'])#数据集2for i in range(0,50):X1=random.randint(0,50)Y1=random.randint(0,50)if(X1+Y1-50>0):lable=1else:lable=-1data1 = data1.append(DataFrame({"X":X1, "Y":Y1, "label":lable},columns = ["X", "Y", "label"],index=[0]),ignore_index=True)#append函数在每列元素下增加一个新生成的元素data1.to_csv('data1.csv',index=False, header=False)#生成数据集1for i in range(0,50):X2=random.randint(0,50)Y2=random.randint(0,50)if(X2+Y2-50>0 and i<45):lable=1elif(X2+Y2-50>0 and i>=45):lable=-1elif(X2+Y2-50<=0 and i<45):lable=-1elif(X2+Y2-50<=0 and i>=45):lable=1data2 = data2.append(DataFrame({"X":X2, "Y":Y2, "label":lable},columns = ["X", "Y", "label"],index=[0]),ignore_index=True)#append函数在每列元素下增加一个新生成的元素data2.to_csv('data2.csv',index=False, header=False)#生成数据集2
关于pandas库的使用说明,利用pandas库生成两组数据集,每组数据集有50个数据。其中第一组数据是由直线x+y=50分成两部分,直线上方的数据标记为1,直线下方的数据标记为-1,改组数据为线性可分数据集;第二组数据生成过程基本相同,但对于最后5个数据点,将直线上方数据标记为-1,直线下方数据标记为1.(存在着一定的随机性,并不能保证数据一定线性不可分)
2.PLA算法
import numpy as npimport pandas as pdimport timeimport matplotlib.pyplot as plt# 1、导入数据集def loaddata():data1 = pd.read_csv("data1.csv", header=None)samples = data1.iloc[:, :2].values # 取所有行,前两列:2实际上是0:2labels = data1.iloc[:, 2].values # 取所有行,第三列return samples, labels# 2、训练感知机模型# 定义一个PLA算法类class PLA:def __init__(self, x, y): # 初始化函数,x={x1,x2}为点集,y={-1,1}为标签集,a为学习率系数self.x = xself.y = yself.a = 0.1self.b = 0self.w = np.zeros((x.shape[1], 1)) # 初始化权重self.sumexamples = self.x.shape[0]self.sumxdims = self.x.shape[1]def sign(self, w, b, x): # y的函数关系y = np.dot(x, w) + breturn int(y)def update(self, ylable, xdata): # 更新W,bdeltaw = ylable * self.a * xdatadeltaw = deltaw.reshape(self.w.shape)self.w = self.w + deltawself.b = self.b + ylable * self.adef train(self): # 训练数据集isFind = False # 开始前没有找到合适分区num = 0while not isFind: # 定义标志位isFind,当while真,则进行下面操作,赋予标志位真count = 0for i in range(self.sumexamples):yt = self.sign(self.w, self.b, self.x[i, :])if (yt * self.y[i] <=0): # 错误分类的情况,如果不设置等于零的话,初始化后就不能迭代了print('第', num, '次错误分类的点为:', self.x[i, :], '此时的w和b为:', self.w, self.b)count += 1num += 1self.update(self.y[i], self.x[i, :])if count == 0:print('最终训练得到的w和b为:', self.w, self.b)isFind = Truereturn self.w, self.b
2.1PLA算法伪代码:
1.(二维情况下)设为数据集,
为横坐标,
为纵坐标,权重系数为
.初始化参数,设
.从
开始循环,直至
2.判断是否有,若等式成立则进行第3步,否则进行第四步。
3.,回到第2步;
时,break.
4.更新:
,
,回到第二步;
附:1.class类的init函数使用方法
2.2算法可视化表示:
#3.画图显示class picture:def __init__(self,data,w,b,l):self.b=bself.w=wplt.figure(1)plt.title('PLA算法',size=15)plt.xlabel('x',size=10)plt.ylabel('y',size=10)xData = np.linspace(0, 50, 100, endpoint=True) # 生成横坐标yData = self.expression(xData)plt.plot(xData, yData, color='r', label='分类线')plt.scatter(data[5][0], data[5][1], color='b', s=50, label='+1')plt.scatter(data[0][0], data[0][1], color='g', s=50, marker='*', label='-1')for i in range(0, len(l)):if (l[i] > 0):plt.scatter(data[i][0], data[i][1], color='b', s=50)else:plt.scatter(data[i][0], data[i][1], color='g', s=50, marker='*')plt.savefig('PLA.png', dpi=75)plt.legend(loc='upper left')#标签位置def expression(self, x):y = (-self.b - self.w[0] * x) / self.w[1] # 注意在此,把x0,x1当做两个坐标轴,把x1当做自变量,x2为因变量,由此生成直线return ydef Show(self):plt.show()plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签plt.rcParams['axes.unicode_minus']=False #这两行需要手动设置
附:2.Python 绘图包 Matplotlib Pyplot 教程
2.3算法计算耗时:
if __name__ == '__main__':start = time.time()samples, labels = loaddata()mypla = PLA(x=samples, y=labels)weights, bias = mypla.train()costtime = time.time() - startprint("Time used:", costtime)picture = picture(samples, weights, bias,labels)picture.Show()
3.Pocket算法
import numpy as npimport pandas as pdimport timeimport matplotlib.pyplot as pltimport random# 1、导入数据集def loaddata():data1 = pd.read_csv("data2.csv", header=None)samples = data1.iloc[:, :2].values # 取所有行,前两列:2实际上是0:2labels = data1.iloc[:, 2].values # 取所有行,第三列return samples, labels# 2、训练感知机模型# 定义一个Pocket算法类class Pocket:def __init__(self, x, y): # 初始化函数,x={x1,x2}为点集,y={-1,1}为标签集,a为学习率系数self.x = xself.y = yself.a = 1self.b = 0self.w = np.zeros((x.shape[1], 1)) # 初始化权重self.best_w = np.zeros((x.shape[1], 1)) # 设置一个误分类点最少的最佳权重用于比较self.best_b = 0self.sumexamples = self.x.shape[0]self.sumxdims = self.x.shape[1]def sign(self, w, b, x): # y的函数关系y = np.dot(x, w) + breturn int(y)def update(self, ylable, xdata): # 更新W,bdeltaw = ylable * self.a * xdatadeltaw = deltaw.reshape(self.w.shape)wc = self.w + deltaw#用于比较的中间值bc= self.b + ylable * self.aif (len(self.countnum(self.best_w, self.best_b)) >= (len(self.countnum(wc, bc)))):self.best_w=self.w + deltawself.best_b=self.b + ylable * self.aself.w=self.w+deltawself.b=self.b+ ylable * self.adef countnum(self,w,b):mistakes=[]for i in range(self.sumexamples):Y=self.sign(w, b, self.x[i, :])if (Y*self.y[i] <=0):#误分类点mistakes.append(i)return mistakesdef train(self,number): # 训练数据集isFind = False # 开始前没有找到合适分区num = 0#循环次数while not isFind: # 定义标志位isFind,当while真,则进行下面操作,赋予标志位真mistakes=self.countnum(self.w,self.b)if (len(mistakes)==0):print('最终训练得到的w和b为:', self.best_w, self.best_b)breakn = mistakes[random.randint(0, len(mistakes) - 1)]self.update(self.y[n], self.x[n, :])print('第', num, '次错误分类的点为:', self.x[n, :], '此时的w和b为:', self.w, self.b)num+=1print('此时误分类点数为',len(mistakes))if num == number:print('最终训练得到的w和b为:', self.best_w, self.best_b)print('最终训练得到的误分类点个数为', len(self.countnum(self.best_w, self.best_b))+1)isFind = Truereturn self.best_w, self.best_b#3.画图显示class picture:def __init__(self,data,w,b,l):self.b=bself.w=wplt.figure(1)plt.title('Pocket算法',size=15)plt.xlabel('x',size=10)plt.ylabel('y',size=10)xData = np.linspace(0, 50, 100, endpoint=True) # 生成横坐标yData = self.expression(xData)plt.plot(xData, yData, color='r', label='分类线')plt.scatter(data[2][0], data[5][1], color='b', s=50, label='+1')plt.scatter(data[0][0], data[0][1], color='g', s=50, marker='*', label='-1')for i in range(0, len(l)):if (l[i] > 0):plt.scatter(data[i][0], data[i][1], color='b', s=50)else:plt.scatter(data[i][0], data[i][1], color='g', s=50, marker='*')plt.savefig('PLA.png', dpi=75)plt.legend(loc='upper left')#标签位置def expression(self, x):y = (-self.b - self.w[0] * x) / self.w[1] # 注意在此,把x0,x1当做两个坐标轴,把x1当做自变量,x2为因变量,由此生成直线return ydef Show(self):plt.show()plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签plt.rcParams['axes.unicode_minus']=False #这两行需要手动设置if __name__ == '__main__':start = time.time()samples, labels = loaddata()mypocket = Pocket(x=samples, y=labels)weights, bias = mypocket.train(10000)costtime = time.time() - startprint("Time used:", costtime)picture = picture(samples, weights, bias,labels)picture.Show()
3.1Pocket算法伪代码:
Pocket算法与PLA算法基本相同,只是由于某些数据不一定是线性可分的,对于这种情况,利用PLA算法将会无限迭代下去,此时就需要在允许一定误差存在的情况下,找到此时最佳的分类直线,由此提出了Pocket算法。其中,Pocket算法与PLA算法最大的区别在于权重系数的更新。
1.(二维情况下)设为数据集,
为横坐标,
为纵坐标,权重系数为
.初始化参数,设
.从
开始循环,直至
2.判断是否有,若等式成立则进行第3步,否则进行第四步。
3.,回到第二步;
时,break.
4.更新:
,进行第五步;
5.判断是否有分类下最佳错误分类点的个数小于
分类下最佳错误分类点的个数,若
误分类点更少,则取其作为最佳权重
,
;否则不改变最佳权重,取
。回到第二步。
最后,为了让程序停下来,我们可以设置一个迭代次数N,迭代N次后算法停止。
4.算法比较
4.1线性可分数据集
首先,两种算法对于线性可分数据集均可找到合适的对数据进行正确的划分,因此可以在设置初始权重为0,学习率
的情况下,对data1进行分类:
| 算法 | 运行时间 | 迭代次数 |
|---|---|---|
| PLA算法 | Time used: 1.3461673259735107 | 9137 |
| Pocket算法 | Time used: 5.010123252868652 | 7318 |
在初始权重为0,学习率的情况下,对data1进行分类:
| 算法 | 运行时间 | 迭代次数 |
|---|---|---|
| PLA算法 | Time used: 0.9483866691589355 | 6646 |
| Pocket算法 | Time used: 2.678621292114258 | 3662 |
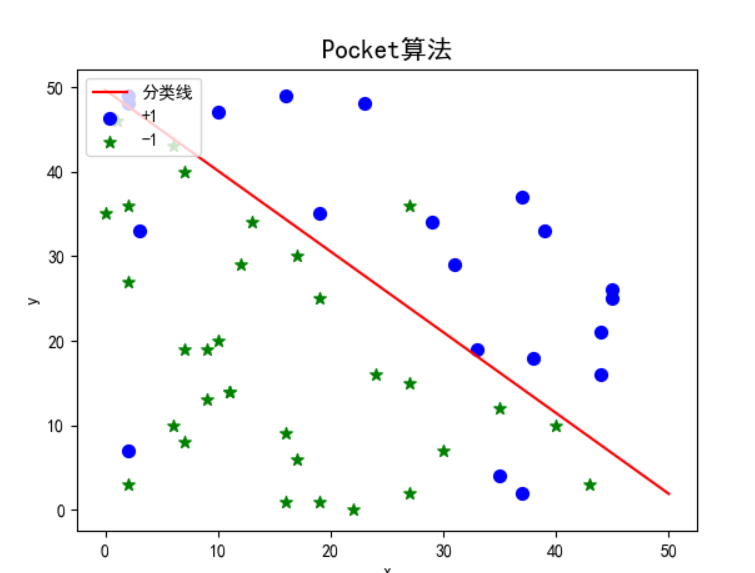
可以发现,两个算法相比,Pocket算法的迭代次数要低于PLA算法,但运行时间要比PLA算法长。迭代次数的不同主要是因为数据点选取的随机性,前期对一些影响小的数据进行了迭代;但是Pocket算法运行时间长是由于,每次进行完权重更新后,需要选出此时的参数与之前最优参数相比下,谁能得到更少的误分类点。两个算法运行结果如下: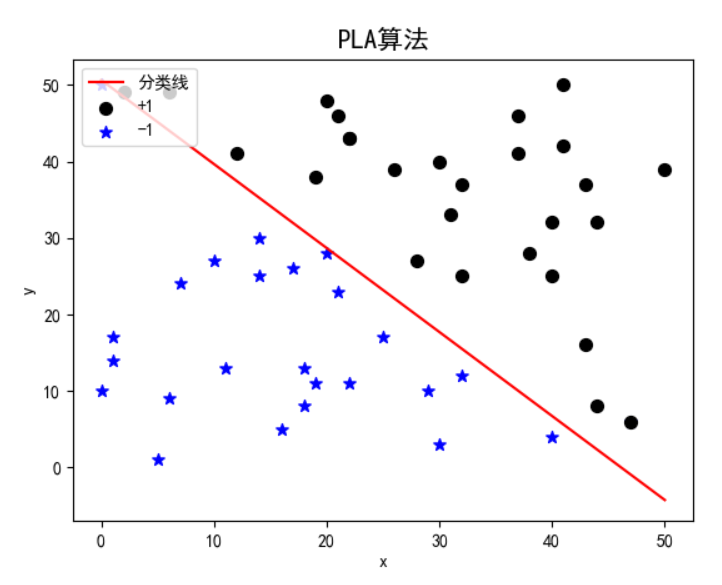
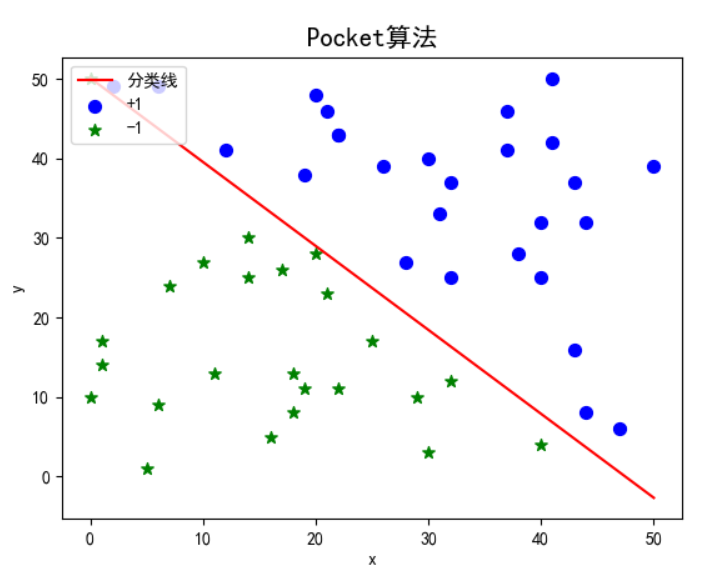
可以发现两个算法都能较好的实现线性可分数据集的分类。
4.2线性不可分数据集
对于线性不可分数据集,PLA算法会无限迭代下去,且每次迭代对会有较强的随机性,基本无法处理此类数据集。可以利用Pocket算法进行分类,求得误分类点最少的情况。
当初始权重为0,学习率的情况下,设置不同迭代上限,对data2进行分类:
| Pocket算法迭代上限 | 运行时间 | 最少误分类点个数 |
|---|---|---|
| 50000 | Time used: 33.37401080131531 | 5 |
| 10000 | Time used: 6.838443040847778 | 6 |
| 5000 | Time used: 3.323680877685547 | 7 |
通过对最优权重的保存,当得到相应迭代次数或者完全正确分类的时候停止,可以发现Pocket算法解决了PLA算法对于存在少数噪点的线性不可分数据集无法停止的情况。对于数据集data2,迭代上限设置在10000到50000次之间时可以得到算法误分类点最少的情况。