Linear Regression

Resources

• homework answer: https://www.kesci.com/home/project/5da16a37037db3002d441810

  Univariate Linear Regression

  Code analyse

  Process data

  #Error: dataSet = pd.read_csv('ex1data1.txt')
  dataSet = pd.read_csv('ex1data1.txt', header=None, names=['Population', 'Profit'])
  dataSet.head()
  dataSet.plot(kind='scatter', x='Population', y='Profit')
  plt.show()

  Define variables

  dataSet.insert(0, 'theta0', 1)
  cols = dataSet.shape[1]
  X = dataSet.iloc[:, :-1]
  y = dataSet.iloc[:, cols-1:cols]
  alpha = 0.01
  iters = 1500
  '''
  以下两种写法可能会导致最后结果不同
  X = np.matrix(X)
  y = np.matrix(y)
  X = np.matrix(X.values)
  y = np.matrix(y.values)
  '''
  X = np.matrix(X.values)
  y = np.matrix(y.values)
  theta = np.matrix(np.array([0,0]))

  cost function

  # Cost function
  def ComputeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    cost = np.sum(inner) / (2 * len(X))
    return cost

  Gradient descent

  def gradientDescent(X, y, theta, alpha, iters):
    parameters = int(theta.ravel().shape[1])
    temp = np.matrix(np.zeros(theta.shape))
    cost = np.zeros(iters)
    for i in range(iters):
        inner = X * theta.T - y
        for j in range(parameters):
            term = np.multiply(inner, X[:,j])
            temp[0,j] = temp[0,j] - alpha * np.sum(term) / len(X)
        theta = temp
        cost[i] = computeCost(X, y, theta)
    return theta, cost
  '''
  return:
  matrix([[-3.63029144,  1.16636235]]),
  array([6.73719046, 5.93159357, 5.90115471, ..., 4.48343473, 4.48341145,
        4.48338826])
  '''

  # Error code
  def gradientDescent2(X, y, theta, alpha, iters):
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)
    for i in range(iters):
        error = (X * theta.T) - y
        for j in range(parameters):
            term = np.multiply(error, X[:,j])
            theta[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
        cost[i] = ComputeCost(X, y, theta)
    return theta, cost
  '''
  return:
  matrix([[0, 0]]),
  array([32.07273388, 32.07273388, 32.07273388, ..., 32.07273388,
        32.07273388, 32.07273388])
  ''''

  Normal equations ```python def normalEqn(X, y): theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X) return theta ‘’’ return: matrix([[-3.89578088], [ 1.19303364]])

梯度下降得到的结果是matrix([[-3.63029144, 1.16636235]]) 正规方程得到的结果是matrix([[-3.89578088], [1.19303364]]) ‘’’ ```

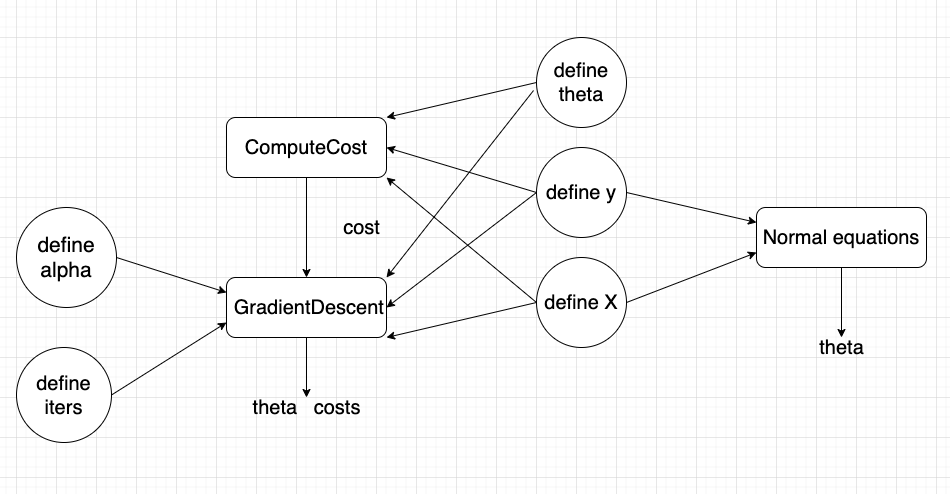
Process chart