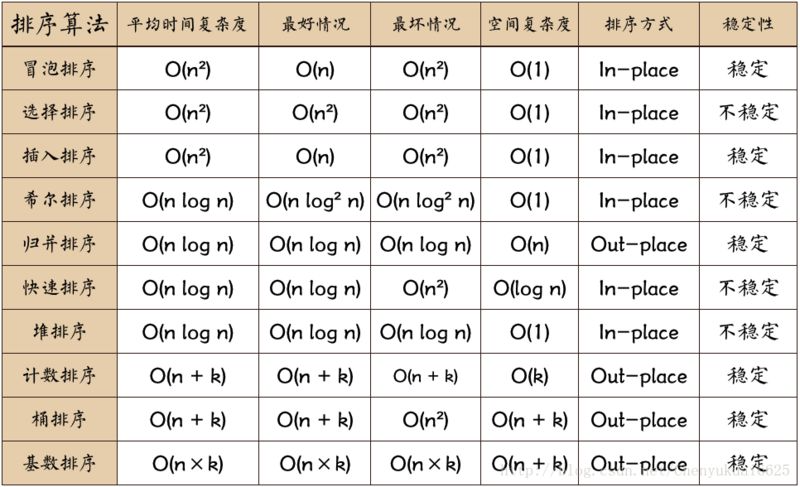
算法复杂程度表
原文链接：
一份清晰又全面的排序算法攻略_程序员小灰的博客-CSDN博客
1）冒泡排序
1.1）冒泡排序思想：
冒泡排序无疑是最为出名的排序算法之一，从序列的一端开始往另一端冒泡（你可以从左往右冒泡，也可以从右往左冒泡，看心情），依次比较相邻的两个数的大小（到底是比大还是比小也看你心情）。
以 [ 8，2，5，9，7 ] 这组数字来做示例，上图来战：
从左往右依次冒泡，将小的往右移动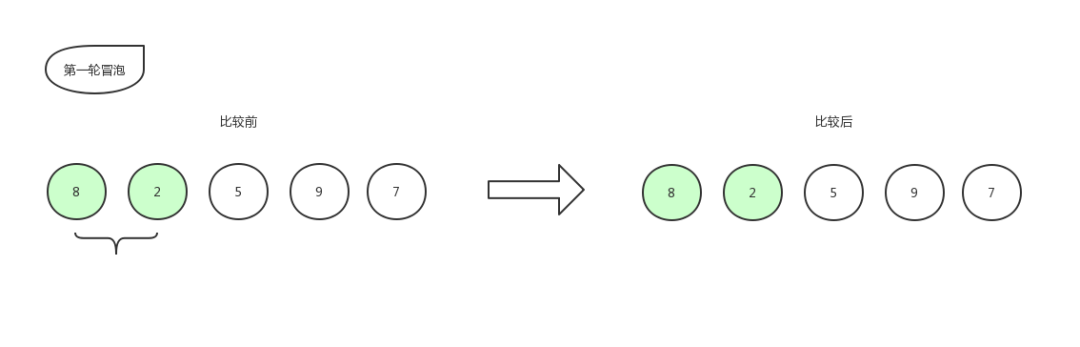
冒泡排序1
首先比较第一个数和第二个数的大小，我们发现 2 比 8 要小，那么保持原位，不做改动。位置还是 8，2，5，9，7 。
指针往右移动一格，接着比较：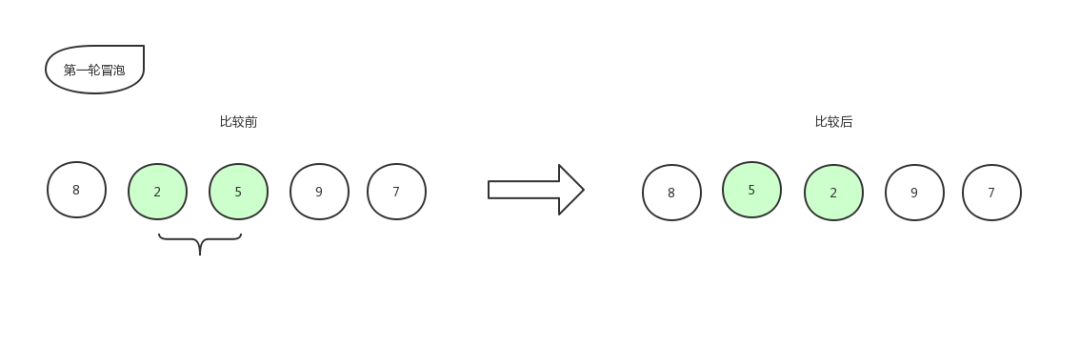
冒泡排序2
比较第二个数和第三个数的大小，发现 2 比 5 要小，所以位置交换，交换后数组更新为：[ 8，5，2，9，7 ]。
指针再往右移动一格，继续比较：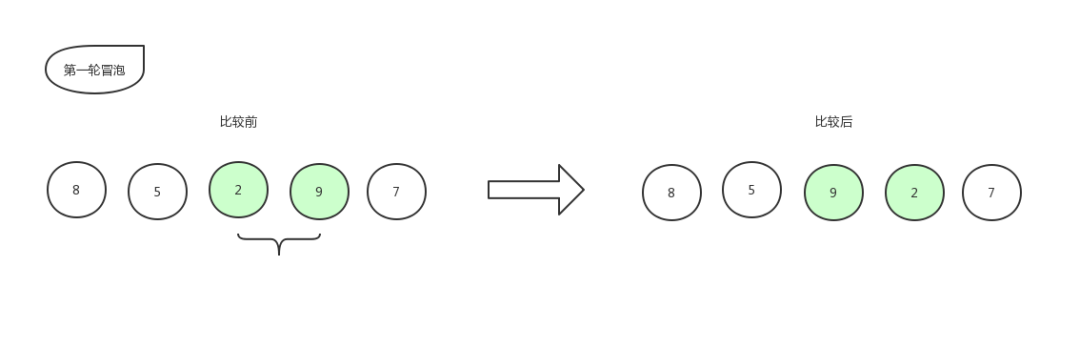
冒泡排序3
比较第三个数和第四个数的大小，发现 2 比 9 要小，所以位置交换，交换后数组更新为：[ 8，5，9，2，7 ]
同样，指针再往右移动，继续比较：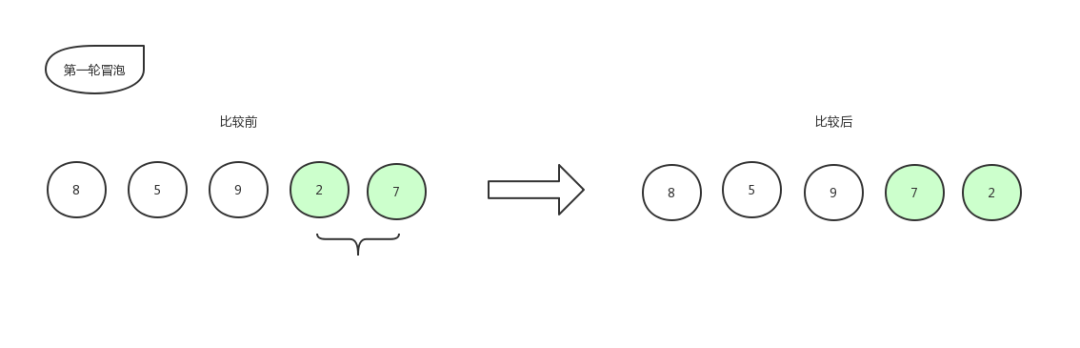
冒泡排序4
比较第 4 个数和第 5 个数的大小，发现 2 比 7 要小，所以位置交换，交换后数组更新为：[ 8，5，9，7，2 ]
下一步，指针再往右移动，发现已经到底了，则本轮冒泡结束，处于最右边的 2 就是已经排好序的数字。
通过这一轮不断的对比交换，数组中最小的数字移动到了最右边。
接下来继续第二轮冒泡：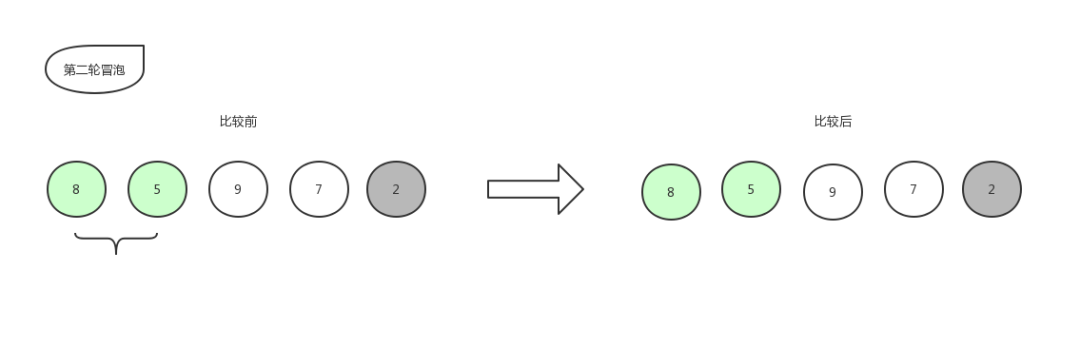
冒泡排序5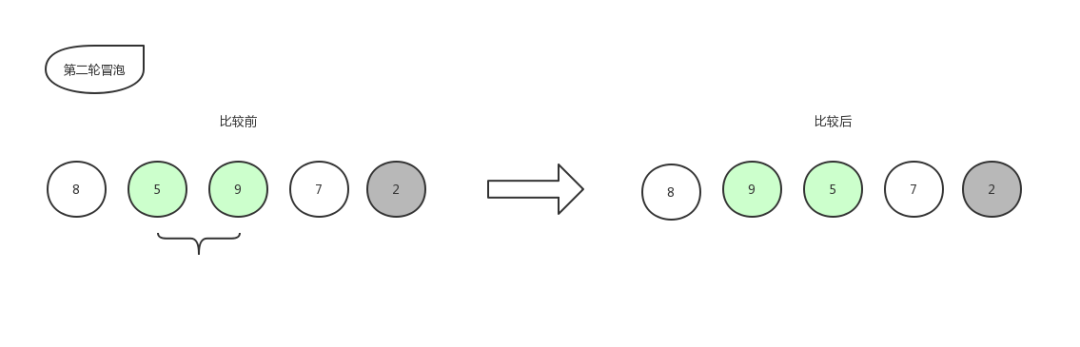
冒泡排序6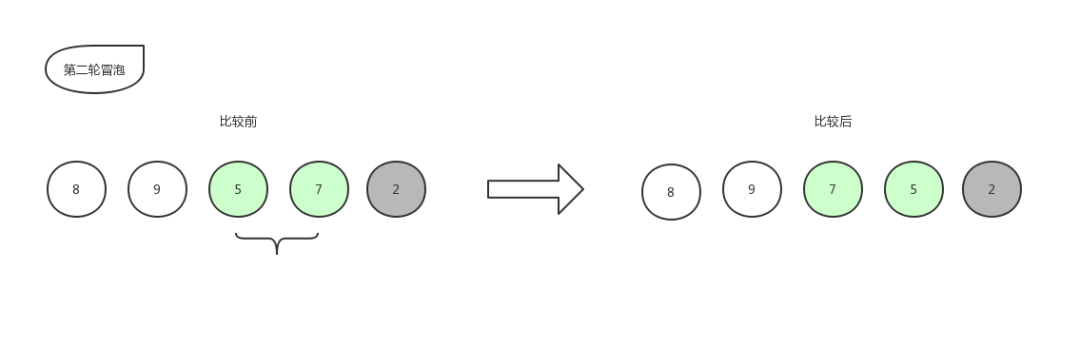
冒泡排序7
由于右边的 2 已经是排好序的数字，就不再参与比较，所以本轮冒泡结束，本轮冒泡最终冒到顶部的数字 5 也归于有序序列中，现在数组已经变化成了[ 8，9，7，5，2 ]。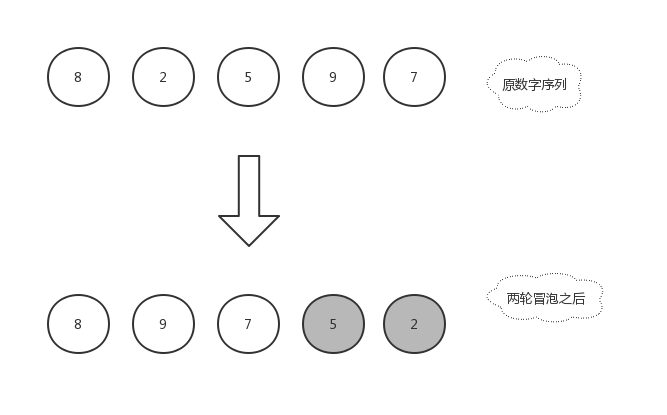
冒泡排序8
让我们开始第三轮冒泡吧！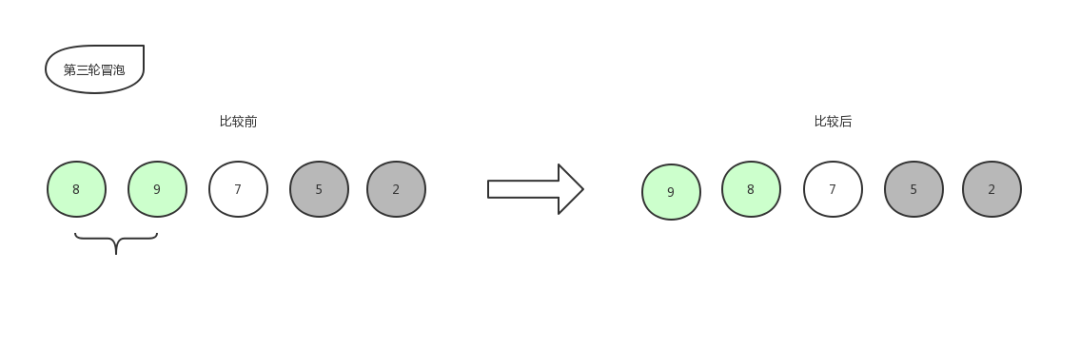
冒泡排序9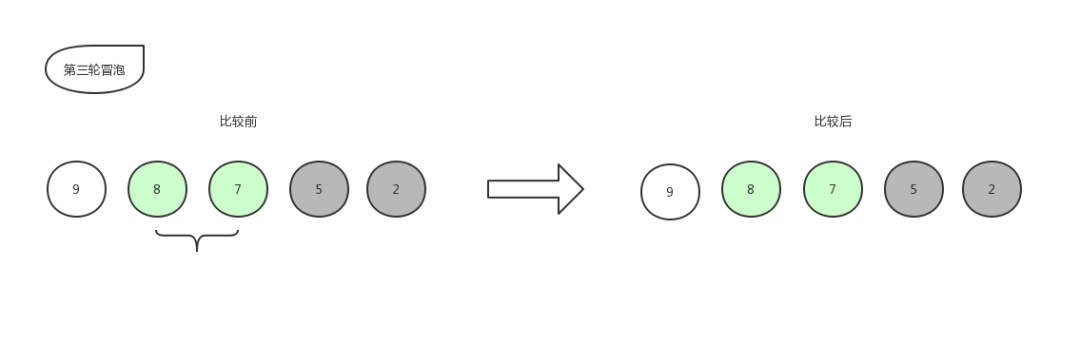
冒泡排序10
由于 8 比 7 大，所以位置不变，此时第三轮冒泡也已经结束，第三轮冒泡的最后结果是[ 9，8，7，5，2 ]
紧接着第四轮冒泡：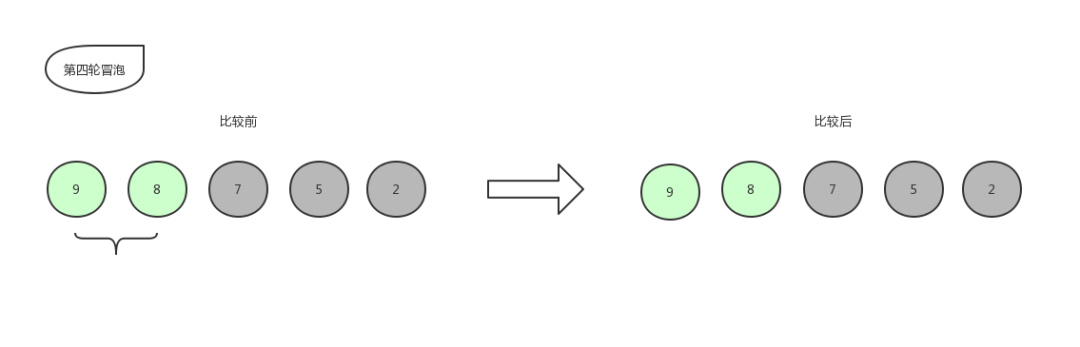
冒泡排序11
9 和 8 比，位置不变，即确定了 8 进入有序序列，那么最后只剩下一个数字 9 ，放在末尾，自此排序结束。
1.2) 时间复杂度：
冒泡的代码还是相当简单的，两层循环，外层控制冒泡轮数，里层依次比较和交换位置，江湖中人人尽皆知。
我们看到嵌套循环，应该立马就可以得出这个算法的时间复杂度为O(n2)。
1.3）冒泡排序代码：
冒泡的代码还是相当简单的，两层循环，外层冒泡轮数，里层依次比较和交换位置，江湖中人人尽皆知。
/*** 冒泡排序* 1，每一个元素和它右边的元素进行比较，* 如果比右边的元素大，则交换位置，然后该元素继续和右边的元素进行比较；* 如果比右边的元素小，则换成右边的该较大的元素继续往右比较；* 2，这样，每一轮冒泡之后--(元素的比较和位置交换)，当前轮中最大的元素都一定在最右边的位置了；* @param arr*/public static void maopao(int[] arr) {//1，遍历数组：//i是外循环控制轮数：for (int i = 0; i < arr.length; i++) {//j循环里边进行元素的比较和位置交换//因为是j和j+1进行比较，所以 j < arr.length-1//因为每一轮冒泡之后--(元素的比较和位置交换)，最大、第二大、第三大...的元素都一定在最右边的位置了， 所以那些右边冒过泡的元素都不需要再次进行比较了，所以j < arr.length-1-ifor (int j = 0; j < arr.length-1-i; j++) {//如果比后边的元素大，则交换位置，然后该元素继续和后边的元素进行比较；if (arr[j] > arr[j+1]) {int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;continue;}//如果比后边的元素小，则换成后边的该较大的元素继续往后比较；else{continue;}}}}
1.4）冒泡排序优化：
2）选择排序：
2.1）选择排序思想：
选择排序的思路是这样的：
首先，找到数组中最小的元素，拎出来，将它和数组的第一个元素交换位置，
第二步，在剩下的元素中继续寻找最小的元素，拎出来，和数组的第二个元素交换位置，
…
如此循环，直到整个数组排序完成。
至于选大还是选小，这个都无所谓，你也可以每次选择最大的拎出来排，也可以每次选择最小的拎出来的排，只要你的排序的手段是这种方式，都叫选择排序。
图解：
我们还是以[ 8，2，5，9，7 ]这组数字做例子。
第一次选择，先找到数组中最小的数字 2 ，然后和第一个数字交换位置。（如果第一个数字就是最小值，那么自己和自己交换位置，也可以不做处理，就是一个 if 的事情）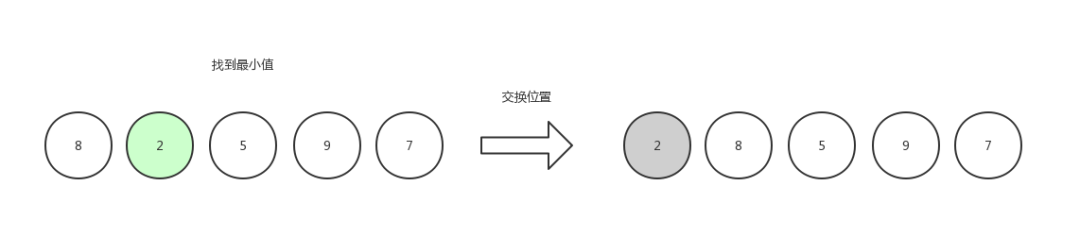
选择排序1
第二次选择，由于数组第一个位置已经是有序的，所以只需要查找剩余位置，找到其中最小的数字5，然后和数组第二个位置的元素交换。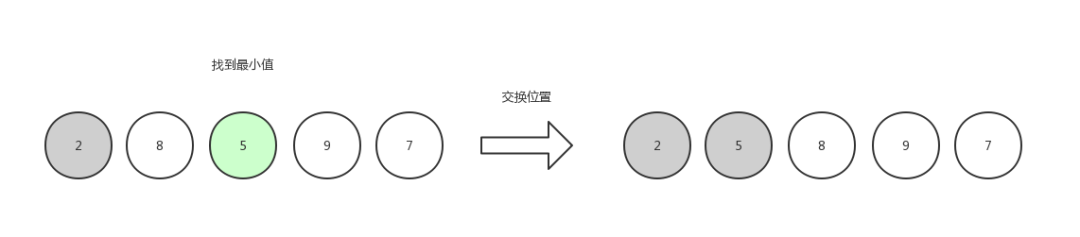
选择排序2
第三次选择，找到最小值 7 ，和第三个位置的元素交换位置。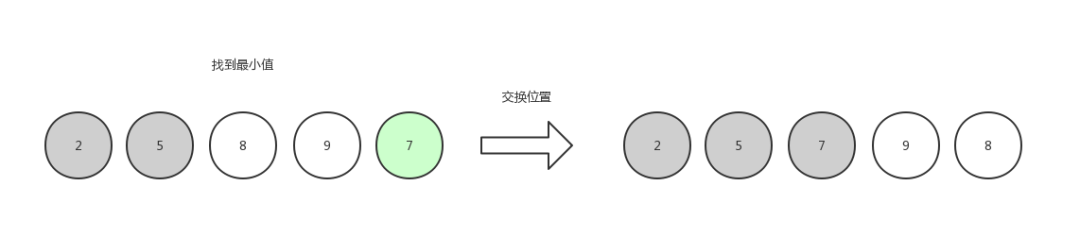
选择排序3
第四次选择，找到最小值8，和第四个位置的元素交换位置。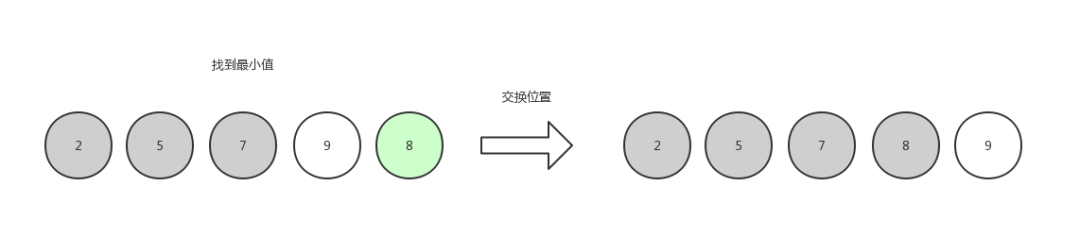
选择排序4
最后一个到达了数组末尾，没有可对比的元素，结束选择。
如此整个数组就排序完成了。
2.2）选择排序：（自己理解）
（以从小到大为例）
总结：
一直选择“第i位置”为当前数组中最小的元素：
与后边的元素进行比较，小于则继续遍历，大于则进行元素的交换；
比如：
选择第一个位置，第一个位置的元素成为最小元素之后，
再选择第二个位置，第二个位置的元素成为除第一个位置所在元素之外最小的数之后，再选择第三个数…
步骤：
从i=0开始，让数组中的第i位置的元素，依次与它后面的那些元素们进行比较，
- 如果第一个位置的元素小于等于后面的元素，则继续往后遍历；
- 如果第一个位置的元素大于后面的元素，则进行位置的交换。
- 【交换之后，此时第一个位置所在元素成为较小元素，然后继续和后面的元素进行比较，重复步骤1和步骤2】
这样多轮内循环结束之后，数组中第一个位置就一定是最小的元素了；
之后，i++，让数组中的第i位置的元素，再依次与它后面的那些元素们进行比较，内循环之后，数组中第二个位置的元素就选出来了；
……
不理解的看看图应该就差不多了：
2.3）选择排序的时间复杂度
2.4）选择排序代码：
/**
* 选择排序：（外层控制 选择的位置，内层进行 该位置所在元素 与 其他的元素 进行比较与交换）
* 1，选出当前数组中最小的数在第一个位置；
* 2，除了第一个位置之外，选择当前数组中最小的数在第二个位置；
* ...
* 3，最终，完成排序；
*
* @param arr
*/
public static void xuanzepaixu(int[] arr) {
//遍历数组：
//i < arr.length-1; 最后一个元素不需要去进行选择排序了；
for (int i = 0; i < arr.length-1; i++) {
//选择第i位置为当前数组中最小的元素；
for (int j = i + 1; j < arr.length; j++) {
//如果arr[i]>arr[j]，则进行位置交换，然后第i位置的元素继续和后边的元素进行比较
if (arr[i] > arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//如果arr[i]<=arr[j]，说明第i位置的元素是较小的，则继续往后进行比较；
else{
continue;
}
}
}
}
3）插入排序：
3.1）插入排序思想：
插入排序的思想和我们打扑克摸牌的时候一样，从牌堆里一张一张摸起来的牌都是乱序的，我们会把摸起来的牌插入到左手中合适的位置，让左手中的牌时刻保持一个有序的状态。
那如果我们不是从牌堆里摸牌，而是左手里面初始化就是一堆乱牌呢？
一样的道理，我们把牌往手的右边挪一挪，把手的左边空出一点位置来，然后在乱牌中抽一张出来，插入到左边，再抽一张出来，插入到左边，再抽一张，插入到左边，每次插入都插入到左边合适的位置，时刻保持左边的牌是有序的，直到右边的牌抽完，则排序完毕。
数组初始化：[ 8，2，5，9，7 ]，我们把数组中的数据分成两个区域，已排序区域和未排序区域，初始化的时候所有的数据都处在未排序区域中，已排序区域是空。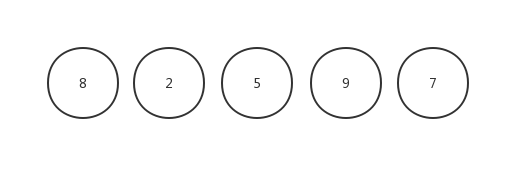
插入排序1
第一轮，从未排序区域中随机拿出一个数字，既然是随机，那么我们就获取第一个，然后插入到已排序区域中，已排序区域是空，那么就不做比较，默认自身已经是有序的了。（当然了，第一轮在代码中是可以省略的，从下标为1的元素开始即可）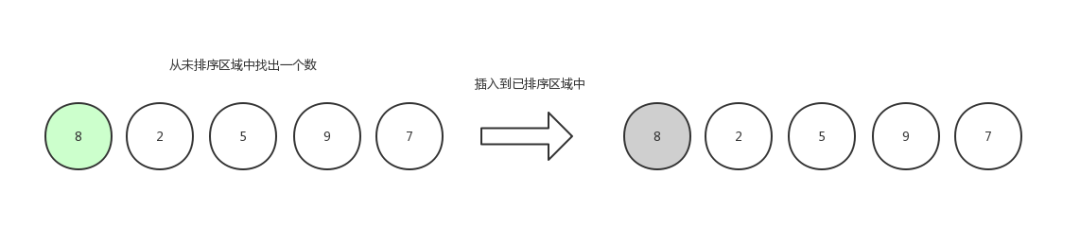
插入排序2
第二轮，继续从未排序区域中拿出一个数，插入到已排序区域中，这个时候要遍历已排序区域中的数字挨个做比较，
比大比小取决于你是想升序排还是想倒序排，这里排升序：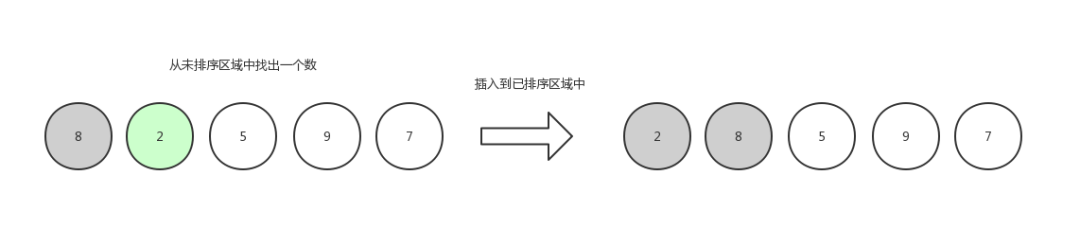
插入排序3
第三轮，排 5 ：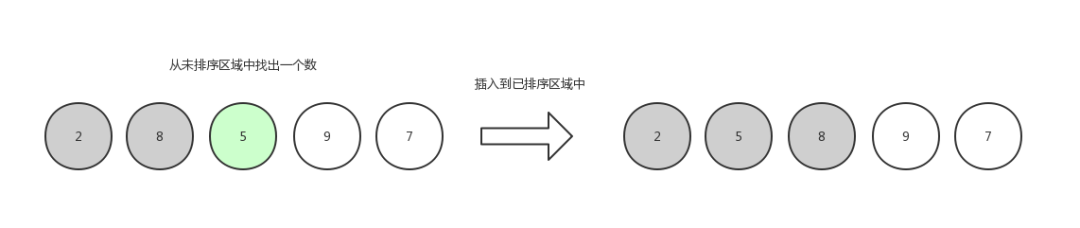
插入排序4
第四轮，排 9 ：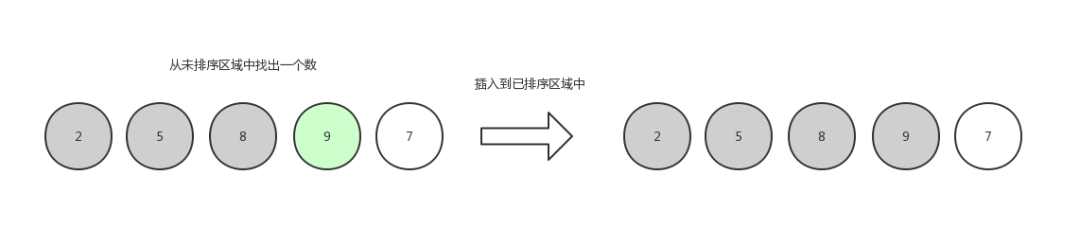
插入排序5
第五轮，排 7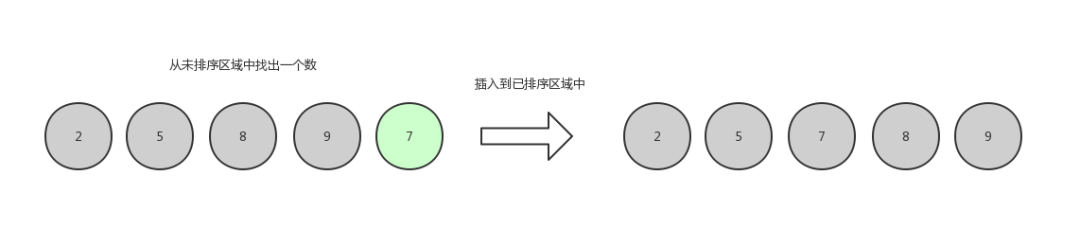
插入排序6
排序结束。
3.2）插入排序时间复杂度：
从代码里我们可以看出，如果找到了合适的位置，就不会再进行比较了，就好比牌堆里抽出的一张牌本身就比我手里的牌都小，那么我只需要直接放在末尾就行了，不用一个一个去移动数据腾出位置插入到中间。
所以说，最好情况的时间复杂度是 O(n)，最坏情况的时间复杂度是 O(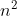
)，
然而时间复杂度这个指标看的是最坏的情况，而不是最好的情况，所以插入排序的时间复杂度是 O(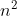
)。
3.3）插入排序代码：
插入排序：(从小到大排列)
将数组分为两个部分，一个部分是排好序的，一个部分是未排序的，不断的将未排序的元素插入到排好序的那一部分中，最终完成排序；
- 第一位元素不用插入，从第二位开始-往左遍历和插入；
- 以i为边界，i以及i左边是已排好序的部分，i右边的是未排序的部分；
- 将待插入元素插入到已排好序的部分—从右往左遍历(方便大于待插入元素的元素的右移)
3.3.1，如果待插入元素小于当前遍历元素，则：当前遍历元素右移一位，待插入元素暂时插入到当前遍历元素的原位置，然后插入元素继续往左遍历；
3.3.2，如果待插入元素大于当前遍历元素，则此时正好当前遍历元素的右边紧邻位置就是待插入元素，则此轮插入完成；
/**
* 插入排序：（从小到大排序）
* 1，第一位元素不用插入，从第二位开始-往左遍历和插入；
* 2，以i为边界，i以及i左边是已排好序的部分，i右边的是未排序的部分；
* 3，将待插入元素插入到已排好序的部分--从右往左遍历--(方便大于待插入元素的元素的右移)
* 3.1，如果待插入元素小于当前遍历元素，则当前遍历元素右移一位，待插入元素暂时插入到当前遍历元素的原位置，然后插入元素继续往左遍历；
* 3.2，如果待插入元素大于当前遍历元素，则此时正好当前遍历元素的右边紧邻位置就是待插入元素，则此轮插入完成；
*
* @param arr
*/
public static void charuPaiXu2(int[] arr) {
//i < arr.length - 1是因为代码中有 arr[i + 1]，且i为最后一个元素时就说明已经排好序了；
for (int i = 0; i < arr.length - 1; i++) {
//将待插入元素复制出来一份，防止被覆盖
int daicharuEle = arr[i + 1];
//从右往左遍历比较已排好序的部分：
for (int j = i; j >= 0; j--) {
//如果待插入元素小于当前元素：
if (daicharuEle < arr[j]) {
//将当前元素右移，将待插入元素暂时插入到当前元素的原位置：
arr[j + 1] = arr[j];
arr[j] = daicharuEle;
continue;
}
//如果待插入元素大于当前元素，此时待插入元素正好是在当前元素的右边紧邻位置，本轮插入完成：
else {
break;
}
}
}
}
4）希尔排序：
4.1）希尔排序思想：
希尔排序算法是插入排序算法的一种，又叫作缩小增量排序算法，是插入排序算法的一种更高效的改进版本，也是非稳定排序算法。
希尔排序算法将数组按下标的一定增量进行分组，对每个子数组使用插入排序算法排序。
示意图：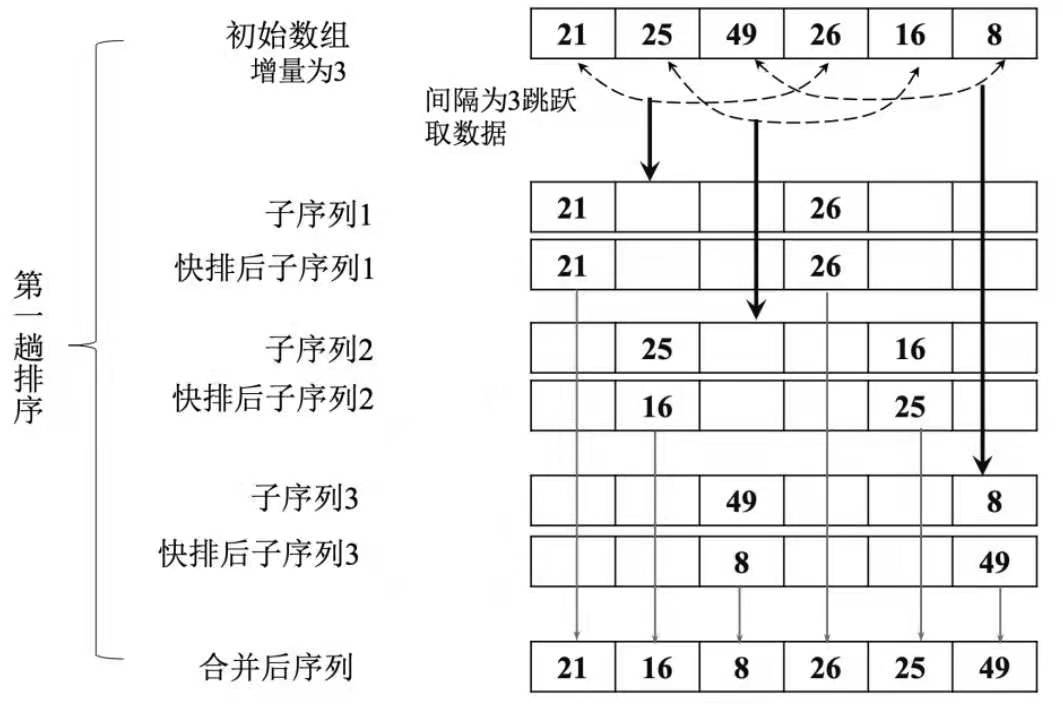
希尔排序算法的具体做法：
假设待排序元素序列有N个元素，则先取一个小于N的整数增量值increment作为间隔，比如说increment=arr.length/2，将全部元素分为increment个子序列，
将所有距离为increment的元素都放在同一个子序列中，在每一个子序列中分别实行直接插入排序；
然后缩小间隔increment，重复上述子序列的划分和排序工作，
直到最后取increment=1，将所有元素都放在同一个子序列中时，执行最后一次插入排序终止。
从直观上看希尔排序：
- 就是把数列进行分组(不停使用插入排序)，直至从宏观上看起来有序，最后插入排序起来就容易了(无须多次移位或交换)。
那么，上面那里说了将一个序列分成好几个序列，那么到底怎么分呢？比如有10个元素的序列，分成几个才合适？每次缩减又是多少呢？
从专业的角度上讲，将一个序列分成好几个序列，用一个数来表示：那个数称为增量。显然的是，增量是不断递减的(直到增量为1)
往往的：
如果一个数列有10个元素，我们第一趟的增量是5，第二趟的增量是2，第三趟的增量是1。
如果一个数列有18个元素，我们第一趟的增量是9，第二趟的增量是4，第三趟的增量是2，第四趟的增量是1
很明显我们可以用一个序列来表示增量：{n/2,(n/2)/2…1}，每次增量都/2；
举例：
现在我们有一个数组，该数组有6个元素
int[] arrays = {2, 5, 1, 3, 4, 6};
排序前：
- 将该数组看成三个（arrays.length/2)数组，分别是: {2,3},{5,4},{1,6}
第一趟排序：
- 对三个数组分别进行插入排序，因此我们三个数组得到的结果为{2,3},{4,5},{1,6} ；
- 此时数组是这样子的：{2, 4, 1, 3, 5, 6}
第二趟排序：
- 增量减少了，上面增量是3，此时增量应该为1了，因此把{2, 4, 1, 3, 5, 6}看成一个数组(从宏观上是有序的了)，对其进行插入排序，直至有序。
最后：
我们发现希尔排序代码其实非常简单(相比对堆排序)，理解起来也不难，就用增量来将数组进行分隔，直到增量为1。底层干的还是插入排序干的活～
希尔排序的增量选择：
在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，
这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2…1}，称为增量序列。
希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量。
希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；
当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。
希尔排序的特点：
- Shell排序比冒泡排序快5倍，比插入排序大致快2倍。
- Shell排序比起QuickSort快速排序，MergeSort归并排序，HeapSort堆排序慢很多。
- 但是它相对比较简单，它适合于数据量在5000以下并且速度并不是特别重要的场合。对于数据量较小的、原本顺序不是很乱的数列的排序，希尔排序的效果是非常好的。
4.2）希尔排序的时间复杂度：
其最坏时间复杂度依然为O(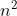
)，
希尔排序的时间复杂度为O(n^1.3)~O(n^2)，平均时间复杂度为O(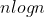
)。
希尔排序的时间复杂度我们计算起来比较复杂，所以在这里我们直接记住这个结论即可:
1，在数组整体有序的情况下，希尔排序的时间复杂度是接近o(n^1.3)的；
2，在数组整体逆序的情况下，希尔排序的时间复杂度和插入排序接近，是O(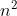
)；
所以，希尔排序的时间复杂度我们进行如下表示:
希尔排序的时间复杂度：O(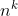
) (1.3<= k <= 2)，平均时间复杂度为O(
)。
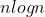注意: 有的同学认为，希尔排序在代码实现的时候，相当于嵌套了3层循环结构，那它的时间复杂程度应该是O(n3)，这种认知是错误的。
通过算法的循环嵌套层数推断算法的事件复杂程度的确是一种技巧，但是并不是百试百灵的。一个算法的时间复杂程度，依然要通过分析算法的基本流程本身才能够得到。
4.3）希尔排序代码：
/**
* 1，设置增量increment，根据increment将数组分为多个子数组：每个元素和该元素的位置+increment所在位置的元素是一组；
* 2，将每个子数组进行插入排序；
* 3，增量increment/2，再次进行划分子数组并对每个子数组进行插入排序；
* 4，直到增量为1的时候，进行最后一次插入排序即可；
*
* @param arr
*/
public static void xierpaixu(int[] arr) {
//1，一共几轮插入排序，每一轮设置一个增量increment，比如说从arr.length/2开始，每一轮increment缩小一半，到1停止；
for (int increment = arr.length / 2; increment >= 1; increment /= 2) {
//对于子数组执行插入排序：
for (int i = 0; i < arr.length-increment; i++) {
//i以及i左边的元素是已排好序的，i右边的是没排好序的：
int daipaixuEle = arr[i + increment];
for (int j = i; j >= 0; j-=increment) {
//如果待排序元素小于当前遍历元素，则当前遍历元素右移increment位，待排序元素暂时插入到当前遍历元素的原位置；
if (daipaixuEle < arr[j]) {
arr[j + increment] = arr[j];
arr[j] = daipaixuEle;
continue;
}
//如果待排序元素大于当前遍历元素，则此时正好待排序元素就在当前遍历元素的右边increment位置，子数组的本轮插入排序结束；
else{
break;
}
}
}
}
}
5）快速排序：
详见：快速排序-学习笔记_Morning sunshine的博客-CSDN博客
6）归并排序：
6.1）归并排序思想：
归并排序 是利用归并的思想实现的排序方法；
该算法采用经典的分治策略：
1、将问题分成一些小的问题然后递归求解；
2、而治 的阶段则将分的阶段得到的各个答案”拼组”在一起，即分而治之)。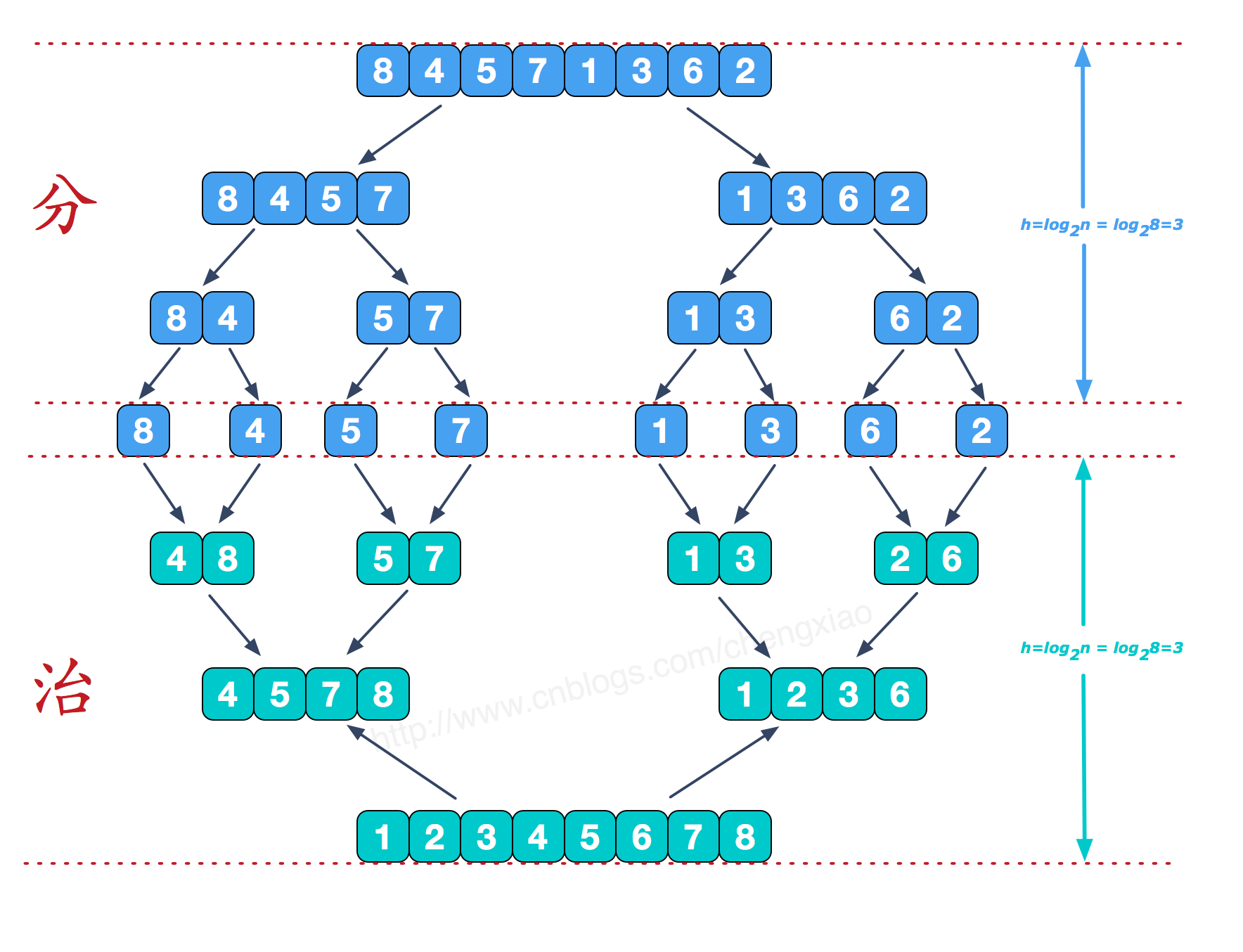
可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。
分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。
基本思想
归并排序的主要思想是分治法。主要过程是：
- 将n个元素从中间切开，分成两部分。（左边可能比右边多1个数）
- 将步骤1分成的两部分，再分别进行递归分解。直到所有部分的元素个数都为1。
- 从最底层开始逐步合并两个排好序的数列。
思考：
考虑一个问题，如何将两个有序数列合并成一个有序数列？
很简单，由于进行合并的时候，由于两个数列本身都已经有序，所以：
- 我们只需从两个数列的低位轮番拿出各自最小的数来PK就行了：
- 输的一方为小值，将这个值放入临时数列，然后输的一方继续拿出一个值来PK，
- 直至有一方没有元素后，将另一方的所有元素依次接在临时数列后面即可。
此时，临时数列为两个数列的有序合并。归并排序中的归并就是利用这种思想。
6.2）归并排序的时间复杂度：
归并排序是稳定排序，它也是一种十分高效的排序，
能利用完全二叉树特性的排序一般性能都不会太差。
java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。
归并排序的时间复杂度为O(n*logn)，推导过程较复杂，不再详述。
PS：快速排序的时间复杂度也是O(n*logn);
从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为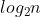
。总的平均时间复杂度为O(nlogn)。
而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。
6.3）归并排序代码：
步骤：
1，首先，将数组不断进行递归分解，直至分为一个一个的元素为最小的子数组；
2，将两个相邻的(有序)子数组，合并为一个新的临时子数组，然后将临时子数组回填到原数组中去；
前提，首先两个子数组肯定是有序的、相邻的；
2.1，当两个子数组中都有元素的时候，从低位进行轮番比较，将较小元素放入临时数组，然后在较小元素所在数组中再取出一个元素，进行再次比较；
2.2，直至其中一个子数组没有元素了，则将另外一个数组的所有剩余元素依次放入临时子数组；
2.3，将临时子数组中的元素回填到原数组中；
3，排序完成；
代码示例：
public class GuiBingPaiXu01 {
public static void main(String[] args) {
int [] arr= new int[]{-9, 78, 100, 21, 41, -421, 23, 33, 78, -2, 33};
guibingpaixu(arr);
System.out.println("Arrays.toString(arr) = " + Arrays.toString(arr));
}
/**
* 归并排序： 分为两个步骤：
* 1，分解，将数组一层一层分解为一个个的单个元素的子数组；
* 2，合并，将这些相邻的子数组进行比较之后，按照顺序合并，
* 3，最终，合并成一个完整的有序数组；
* <p>
* 如何合并两个子数组为一个新的临时子数组：
* 前提，首先两个子数组本身肯定是有序的；
* 2.1，先将两个子数组的最小元素拿出来进行比较，较小者放入临时子数组的首位，
* 2.2，然后较小者所在的子数组继续拿出来第二个元素去进行再次比较；
* 2.3，重复2.1、2.2步骤，直至其中一个子数组没有元素了，则另外一个数组的所有剩余元素直接放入临时子数组；
* 2.4，将临时子数组中的元素回填到原数组中；
* @param arr
*/
private static void guibingpaixu(int[] arr) {
//两个方法：一个分解方法，一个合并方法；
//初始化一个临时数组：
int[] tempArray = new int[arr.length];
fenjie(arr, 0, arr.length - 1, tempArray);
}
/**
* 分解方法：
*/
public static void fenjie(int[] arr, int leftIndex, int rightIndex, int[] tempArray) {
//递归出口：
if (leftIndex < rightIndex) {
fenjie(arr, leftIndex, (leftIndex + rightIndex) / 2, tempArray);
fenjie(arr, (leftIndex + rightIndex) / 2 + 1, rightIndex, tempArray);
//1，当上边的两个递归分解都到了最后一次递归结束，并回溯了一级之后，
// 此时arr[leftIndex]和arr[rightIndex]是两个相邻的单个元素的子数组：
// 对这两个子数组执行合并操作：
//2，当继续往上回溯之后，两个子数组都会包含多个元素，
// 此时两个元素的左边界为leftIndex 和 (leftIndex + rightIndex) / 2 + 1，右边界为(leftIndex + rightIndex) / 2 和 rightIndex；
hebing(arr, leftIndex, (leftIndex + rightIndex) / 2, (leftIndex + rightIndex) / 2 + 1, rightIndex, tempArray);
}
//分解到最后一次时，此时leftIndex == rightIndex，说明此时只有一个元素了，
// 只有一个元素当然不需要合并，所以停止递归分解；
else {
return;
}
}
/**
* 将两个子数组合并为一个新的临时子数组
* （两个子数组一定是相邻着的）
*
* @param arr 数组
* @param leftIndexA 子数组A左边界
* @param rightIndexA 子数组A右边界
* @param leftIndexB 子数组B左边界
* @param rightIndexB 子数组B右边界
* @param tempArray 临时的新数组，leftIndexA为其左边界，rightIndexB为其右边界
*/
public static void hebing(int[] arr, int leftIndexA, int rightIndexA, int leftIndexB, int rightIndexB, int[] tempArray) {
//边界不能动，设置两个子数组的游标：
int leftYouBiaoA = leftIndexA;
int leftYouBiaoB = leftIndexB;
//初始化临时数组的左游标：
int tempLeftYouBiao = leftIndexA;
//当两个子数组中都有元素的时候，进行比较，并将较小元素放入临时数组，并在较小元素所在数组再取出一个元素进行再次比较；
while (leftYouBiaoA <= rightIndexA && leftYouBiaoB <= rightIndexB) {
if (arr[leftYouBiaoA] < arr[leftYouBiaoB]) {
//将两个子元素的较小元素放入临时数组，
tempArray[tempLeftYouBiao] = arr[leftYouBiaoA];
tempLeftYouBiao++;
leftYouBiaoA++;
}else{
//将两个子元素的较小元素放入临时数组，
tempArray[tempLeftYouBiao] = arr[leftYouBiaoB];
tempLeftYouBiao++;
leftYouBiaoB++;
}
}
//当A数组已经没有元素之后，将B数组剩余的元素依次放入临时数组：
while (leftYouBiaoA > rightIndexA && leftYouBiaoB <= rightIndexB) {
tempArray[tempLeftYouBiao] = arr[leftYouBiaoB];
tempLeftYouBiao++;
leftYouBiaoB++;
}
//当B数组已经没有元素之后，将A数组剩余的元素依次放入临时数组：
while (leftYouBiaoA <= rightIndexA && leftYouBiaoB > rightIndexB) {
tempArray[tempLeftYouBiao] = arr[leftYouBiaoA];
tempLeftYouBiao++;
leftYouBiaoA++;
}
//两个数组都一起结束了的情况不会出现，因为肯定会有一个数组先一步到达右边界；
//最后，将临时子数组中的所有元素依次赋值到原数组中：
for (int i = leftIndexA; i <=rightIndexB; i++) {
arr[i] = tempArray[i];
}
}
}
·
·
若有收获，就点个赞吧
0 人点赞
