原文链接:
一,前言
1,什么是快速排序:
快速排序是从冒泡排序演变而来的一种排序算法,比冒泡排序要高效得多,所以叫快速排序。
那么快速排序比冒泡排序快在哪里呢?
快速排序之所以快速,在于他使用了【分治法】。
同冒泡排序一样,快速排序也属于交换排序,通过元素之间的比较和交换位置来达到排序的目的。
不同的是,冒泡排序在每一轮只把一个元素冒泡到数列的一端,
而快速排序在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成了两个部分。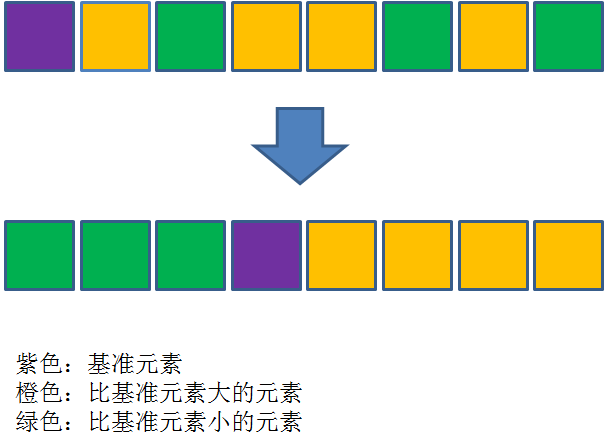
这种思路就叫做分治法。
每次把数列分成两部分,究竟有什么好处呢?
假如给定8个元素的数列,一般情况下冒泡排序需要比较8轮,每轮把一个元素移动到数列一端,时间复杂 度是O(n^2)。
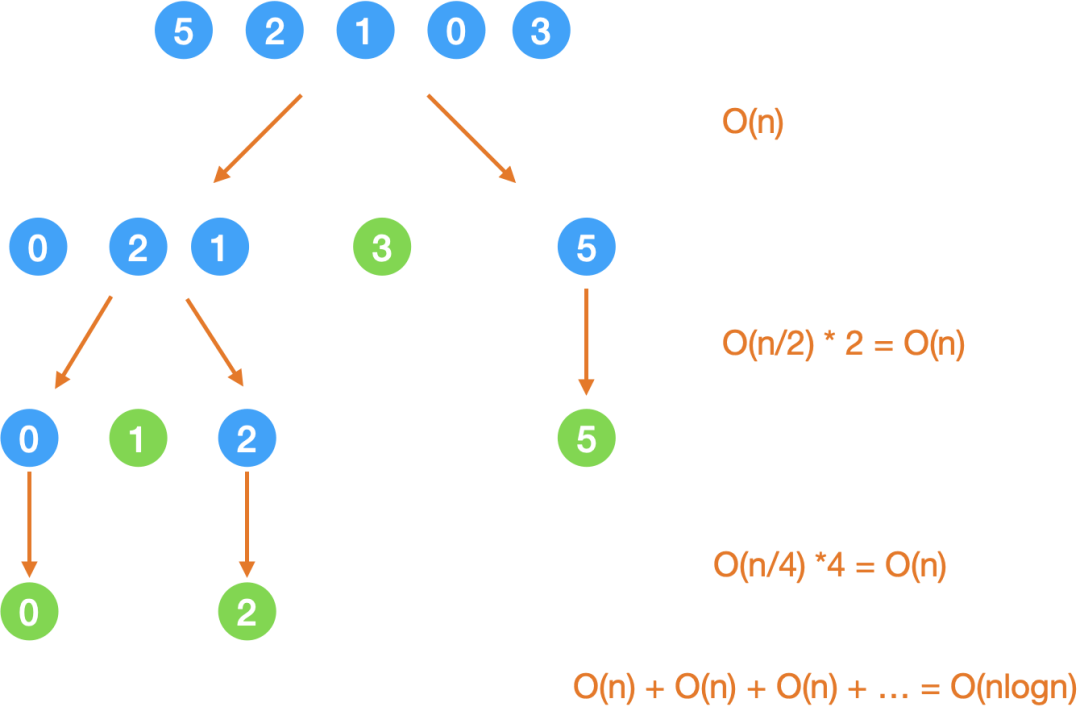
而快速排序的流程是什么样子呢?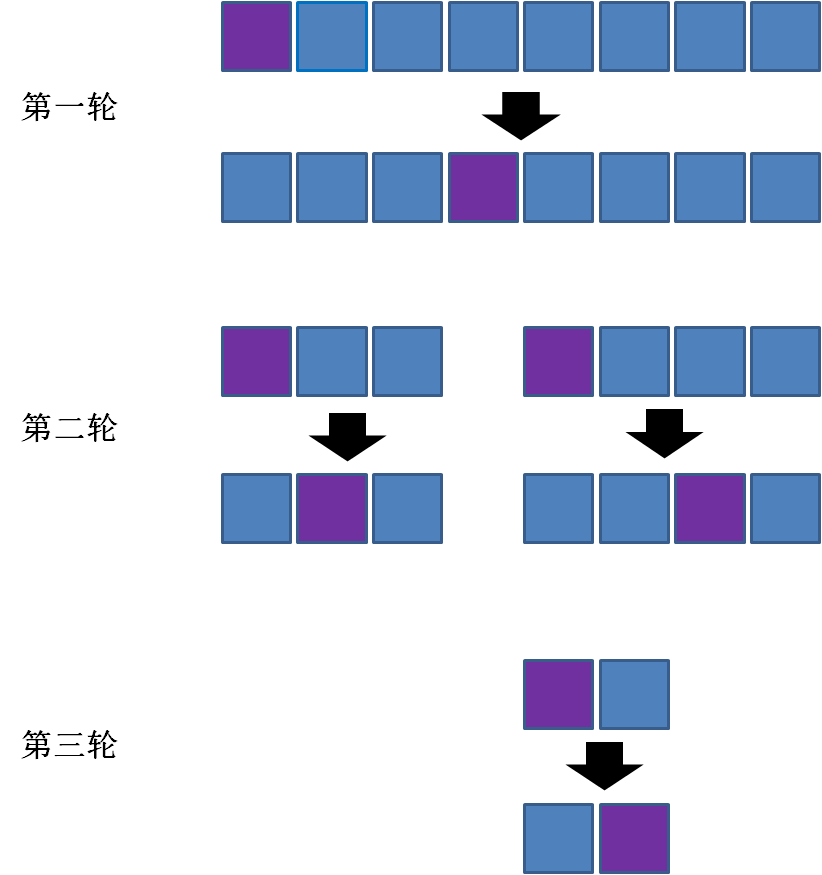
如图所示,在分治法的思想下,原数列在每一轮被拆分成两部分,每一部分在下一轮又分别被拆分成两部分,直到不可再分为止。
这样一共需要多少轮呢?平均情况下需要logn轮,因此快速排序算法的平均时间复杂度是 O(nlogn)。
2,快速排序算法的性能
2.1 理想情况下的时间复杂度:
原文链接:图解排序算法:快速排序
如果每次都能差不多均匀分,那么
- 每次循环的耗时主要就在这个 while 循环里,也就是 O(right - left);
- 均分的话那就是 logn 层;
- 所以总的时间是 O(nlogn).
2.2 时间复杂度
最差情况:
当数据有序时,以第一个关键字为基准分为两个子序列,前一个子序列为空,此时执行效率最差,如果每一轮快排都是如此,那么时间复杂度为n2。
最好情况:
而当数据随机分布时,以第一个关键字为基准分为两个子序列,两个子序列的元素个数接近相等,此时执行效率最好,如果每一轮快排都是如此,那么需要logn轮,时间复杂度为nlogn。
所以,数据越随机分布时,快速排序性能越好;数据越接近有序,快速排序性能越差。
平均情况:
平均情况推算下来稍有点麻烦。如果我的推论讲得不清楚,大家只需要记住:
在平均的情况下,快排的算法复杂度和其在最好的情况下是一样的,都是 O(n⋅logn) 。
区别在于大O表示法中:平均情况下,隐藏的常量会大一点。
平均时间复杂度的计算,详情请参见:
快排的最差情况以及快排平均复杂度的计算 - God is a Coder.. - OSCHINA - 中文开源技术交流社区
2.3 空间复杂度
快速排序在每次分割的过程中,需要 1 个空间存储基准值。而快速排序的大概需要 Nlog2N次的分割处理,所以占用空间也是 Nlog2N 个。
2.4 算法稳定性
在快速排序中,相等元素可能会因为分区而交换顺序,所以它是不稳定的算法。
·
·
3,基准元素的选取是快速排序的核心:


基准元素的选择
基准元素,英文pivot,用于在分治过程中以此为中心,把其他元素移动到基准元素的左右两边。
那么基准元素如何选择呢?
最简单的方式是选择数列的第一个元素:

这种选择在绝大多数情况是没有问题的。但是,假如有一个原本逆序的数列,期望排序成顺序数列,那么会出现什么情况呢?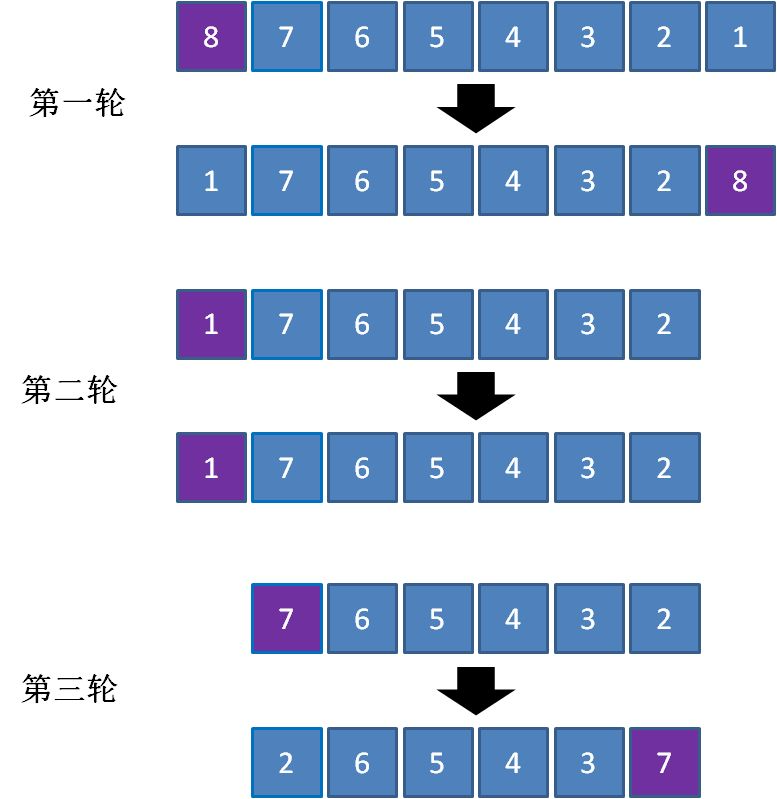
……….


我们该怎么避免这种情况发生呢?
其实很简单,我们可以不选择数列的第一个元素,而是随机选择一个元素作为基准元素。
这样一来,即使在数列完全逆序的情况下,也可以有效地将数列分成两部分。
当然,即使是随机选择基准元素,每一次也有极小的几率选到数列的最大值或最小值,同样会影响到分治的效果。
所以,快速排序的平均时间复杂度是 O(nlogn),最坏情况下的时间复杂度是 O(n^2)。
·
·
4,元素的移动
选定了基准元素以后,我们要做的就是:把数列中小于基准元素的都移动到基准元素一边,大于基准元素的都移动到基准元素另一边。
具体如何实现呢?有两种方法:
- 1.挖坑法
- 2.指针交换法
二,快排—挖坑法
何谓挖坑法?我们来看一看详细过程。
给定原始数列如下,要求从小到大排序:
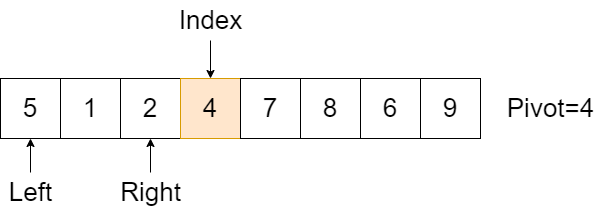
首先,我们选定基准元素Pivot,并记住这个位置index,这个位置相当于一个“坑”。并且设置两个指针left和right,指向数列的最左和最右两个元素:
接下来,从right指针开始,把指针所指向的元素和基准元素做比较。如果比pivot大,则right指针向左移动;**如果比pivot小,则把right所指向的元素填入坑中**。
在当前数列中,1<4,所以把1填入基准元素所在位置,也就是坑的位置。这时候,元素1本来所在的位置成为了新的坑。同时,left向右移动一位。
此时,left左边绿色的区域代表着小于基准元素的区域。
接下来,我们切换到left指针进行比较。如果left指向的元素小于pivot,则left指针向右移动;如果元素大于pivot,则把left指向的元素填入坑中。
在当前数列中,7>4,所以把7填入index的位置。这时候元素7本来的位置成为了新的坑。同时,right向左移动一位。
此时,right右边橙色的区域代表着大于基准元素的区域。
下面按照刚才的思路继续排序:
8>4,元素位置不变,right左移
2<4,用2来填坑,left右移,切换到left。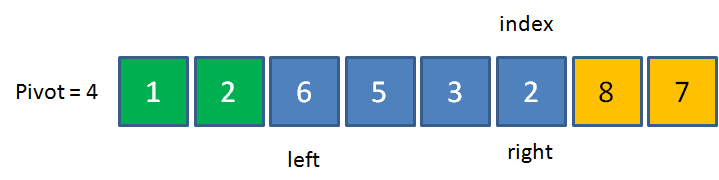
6>4,用6来填坑,right左移,切换到right。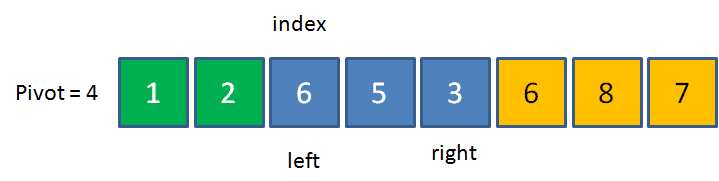
3<4,用3来填坑,left右移,切换到left。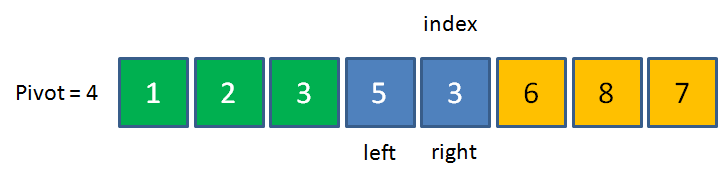
5>4,用5来填坑,right右移。这时候left和right重合在了同一位置。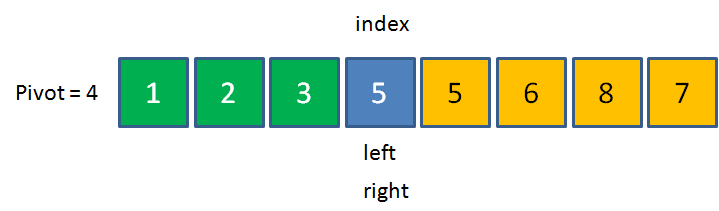
这时候,把之前的pivot元素,也就是4放到index的位置。此时数列左边的元素都小于4,数列右边的元素都大于4,这一轮交换终告结束。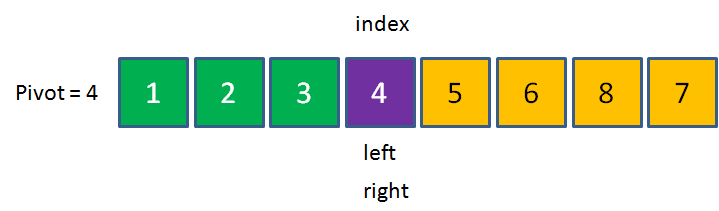


public class KuaiPai13 {
public static void main(String[] args) {
int[] arr = new int[]{4, 7, 6, 5, 3, 2, 8, 1};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
/**
* 快速排序--挖坑法
* @param arr 数组
* @param startIndex 左边界索引
* @param endIndex 右边界索引
*/
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大等于endIndex的时候
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 用分治法递归数列的两部分
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
/**
* 具体每一轮的快速排序:
* @param arr 数组
* @param startIndex 左边界索引
* @param endIndex 右边界索引
* @return 返回基准值的位置,此时基准值左边的元素都小于基准值,基准值右边的元素都大于基准值
*/
private static int partition(int[] arr, int startIndex, int endIndex) {
// 取第一个位置的元素作为基准元素
int pivot = arr[startIndex];
// 初始化坑的位置,初始等于pivot基准值的位置
int kengIndex = startIndex;
//初始化左右游标/指针
int leftYb = startIndex;
int rightYb = endIndex;
//大循环在左右指针重合时结束
while ( leftYb<rightYb ) {
//right指针从右向左进行比较
// leftYb<rightYb ,左游标永远小于右游标,是遍历元素并发生元素变动的前提:
while ( leftYb<rightYb) {
// 先遍历右边,
// 如果元素大于基准值--右游标左移:
if (arr[rightYb] >= pivot) {
rightYb--;
}else{ //如果右边的当前元素小于基准值了,那么将该元素填入坑中,该元素本来的位置成为新的坑;
arr[kengIndex] = arr[rightYb];
kengIndex = rightYb;
leftYb++;
break;
}
}
//再遍历左边,
// leftYb<rightYb ,左游标永远小于右游标,是遍历元素并发生元素变动的前提:
while (leftYb<rightYb) {
//如果元素小于基准值--左游标右移,
if (arr[leftYb] <= pivot) {
leftYb++;
}else{ //如果左边的当前元素大于基准值了,那么将该元素填入坑中,该元素本来的位置成为新的坑;
arr[kengIndex] = arr[leftYb];
kengIndex = leftYb;
rightYb--;
break;
}
}
}
//跳出了大循环,说明此时此刻左右游标是重合的,这时将基准值放在重合位置(最后一个坑),
// 此时,基准值左边的元素都小于基准值,基准值右边的元素都大于基准值,这一轮交换宣告结束;
arr[kengIndex] = pivot;
return kengIndex;
}
}
代码中,quickSort方法通过递归的方式,实现了分而治之的思想。
partition方法则实现元素的移动,让数列中的元素依据自身大小,分别移动到基准元素的左右两边。在这里,我们使用移动方式是挖坑法。
三,指针交换法

指针交换法
何谓指针交换法?我们来看一看详细过程。
给定原始数列如下,要求从小到大排序:
开局和挖坑法相似,我们首先选定基准元素Pivot,并且设置两个指针left和right,指向数列的最左和最右两个元素:
接下来是第一次循环,从right指针开始,把指针所指向的元素和基准元素做比较。如果大于等于pivot,则指针向左移动;
如果小于pivot,则right指针停止移动,切换到left指针。
在当前数列中,1<4,所以right直接停止移动,换到left指针,进行下一步行动。
轮到left指针行动,把指针所指向的元素和基准元素做比较。如果小于等于pivot,则指针向右移动;
如果大于pivot,则left指针停止移动。
由于left一开始指向的是基准元素,判断肯定相等,所以left右移一位。
由于7 > 4,left指针在元素7的位置停下。
这时候,我们让left和right指向的元素进行交换。
接下来,我们进入第二次循环,重新切换到right向左移动。right先移动到8,8>4,继续左移。由于2<4,停止在2的位置。
切换到left,6>4,停止在6的位置。
元素6和2交换。
进入第三次循环,right移动到元素3停止,left移动到元素5停止。
元素5和3交换。
进入第四次循环,right移动到元素3停止,这时候请注意,left和right指针已经重合在了一起。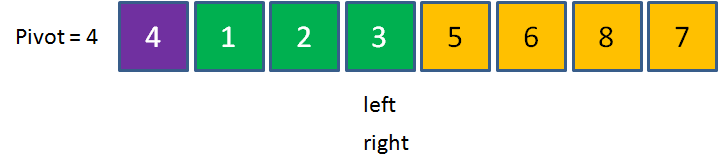
当left和right指针重合之时,我们让pivot元素和left与right重合点的元素进行交换。此时数列左边的元素都小于4,数列右边的元素都大于4,这一轮交换终告结束。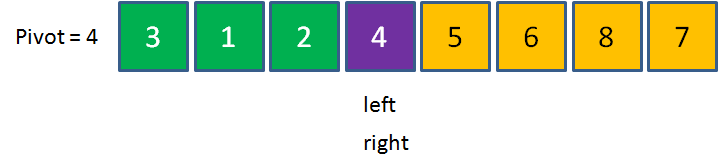


/**
* 快速排序--指针交换法
* @param arr 数组
* @param startIndex 左边界索引
* @param endIndex 右边界索引
*/
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大等于endIndex的时候
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 根据基准元素,分成两部分递归排序
// 用分治法递归数列的两部分
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
/**
* 具体每一轮的快速排序:
* @param arr 数组
* @param startIndex 左边界索引
* @param endIndex 右边界索引
* @return 返回基准值的位置,此时基准值左边的元素都小于基准值,基准值右边的元素都大于基准值
*/
private static int partition(int[] arr, int startIndex, int endIndex) {
// 取第一个位置的元素作为基准元素
int pivot = arr[startIndex];
//初始化左右游标/指针
int leftYb = startIndex;
int rightYb = endIndex;
//大循环在左右指针重合时结束
while (leftYb < rightYb) {
// 先遍历右边, 控制right指针比较并左移
// leftYb<rightYb ,左游标永远小于右游标,是遍历元素并发生元素变动的前提:
while (leftYb < rightYb && arr[rightYb] >= pivot) {
// 如果元素大于基准值--右游标左移:
rightYb--;
}
//跳出了上边while循环,说明此时的右游标所在元素小于基准值
//再遍历左边, 控制right指针比较并右移
// leftYb<rightYb ,左游标永远小于右游标,是遍历元素并发生元素变动的前提:
while (leftYb < rightYb && arr[leftYb] <= pivot) {
//如果元素小于基准值--左游标右移,
leftYb++;
}
//跳出了上边while循环,说明此时的左游标所在元素大于基准值,
//交换左游标和右游标所在位置的元素
if (leftYb < rightYb) {
int temp = arr[leftYb];
arr[leftYb] = arr[rightYb];
arr[rightYb] = temp;
}
}
//跳出了大循环,说明此时此刻左右游标是重合的,
//将pivot基准值和左右游标重合位置的元素进行交换
//arr[startIndex]-->pivot基准值
//这里也可以是arr[rightYb]
int temp = arr[leftYb];
arr[leftYb] = arr[startIndex];
arr[startIndex] = temp;
//返回当前基准值所在位置,
//此时,基准值左边的元素都小于基准值,基准值右边的元素都大于基准值,这一轮快排宣告结束;
return leftYb;
}
四,基准值不是第一个元素的快排
原文链接:笔记(2)—— 面试官:不以第一个元素为基准的快速排序,你会写吗?公众号:流花鬼的博客-CSDN博客快速排序不以第一个数为基准
1)快速排序 的两个过程
首先,记住 快速排序 的两个过程,
- 选择基准
- 元素移动
记住 元素移动 的两种方式,挖坑法 与 指针交换法 ,总结记忆如下,
- 挖坑法 ,动了哪个就一直动哪个,不能动时填坑,填完坑就切换指针,重复直到指针重叠,把基准放进去。开始下一轮。
- 指针交换法,动了哪个就一直动哪个,不能动时,切换指针,都不动的时候交换所指元素,回到初始指针,重复直到指针重叠,与基准交换位置。开始下一轮。
2)快排核心—选择基准值
对于网上大多数的快排基础篇文章,对快速排序的讲解其实已经很深刻了,但之所以,称之为基础篇,因为文章的侧重点是元素移动。
文章告诉你,随机选择基准 可以降低逆序带来的O(n^2)复杂度的可能性,然后实现的时候,,,默默选择了 第一个元素作为基准 ,,,好一个不问来路,只问归处,,,尤其是看了实现代码之后,更是黑人问号??
—— 如果不选择第一个元素为基准,快速排序该怎么写??,网络上大多数文章,也都会告诉你 —— 下面我们选择第一个元素为基准!,真的很气人啊,,,
上文提到,快排的过程是 选择基准——元素移动 ,很显然,基准的选择,会影响元素的移动。
基准的选择,才是快排核心的核心!
首先看下基准选择的三种方式:
- 固定基准 (比如第一个),当原始序列或子序列逆序时,复杂度接近O(n^2),所以应该避免使用这种方式。
- 随机选择 ,降低了逆序复杂度变高的可能性,但仍然不容乐观。
- 三数取中,随机选择三个数,取中间大小的作为基准,当然,本身三个数都是不确定的,随机选择无意义,直接取原始数列的头、中、尾三个元素,得出中间大小作为基准即可。进一步降低了数列逆序的可能性。
可以看到,即使是性能最差的 固定基准 ,也不一定是 选择第一个元素作为基准 ,所以,我们应该掌握的快排,是不以第一个元素为基准的快速排序。
3)不以第一个元素为基准的快速排序,怎么写?
既然,以 第一个元素为基准的快速排序 ,理解和代码实现都是最简单的,那么我们为什么不这样写呢?
无论你使用了哪种 基准选择 的方式,在 元素移动 之前,你都可以让你的 基准 先与 第一个元素 进行 交换,这样是不是就变成了你手到擒来的快速排序?
所以你需要记住快速排序的总过程是:
- 选择基准
- 与第一元素交换
- 元素移动
4)真正不以第一个元素为基准的快速排序,会有很多坑:
本人中了好多次不以第一个元素为基准的快速排序的坑,做一次快排陷进去一次,,,
细心的同学可能会疑惑 —— 你说以 第一个元素为基准的快速排序最简单 ,选择基准后先转化成这种形式,可以理解,但是,如果我不转化成 第一个元素为基准 我就不能写了吗?
当然可以,但是会有很多坑,理解和代码实现都会变得复杂很多,下面我们将会进行 又臭又长 的分析。
上面的内容已经足够让你 记住并写出正确的快速排序 ,如果你没有这些疑惑,可以直接忽略下面这些 又臭又长 的分析。
4.1)挖坑法 — 随机选择基准
如果直接按照 第一个元素为基准的挖坑法 的实现代码,去实现随机选择基准的快排:
public class QuickSort {
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大等于endIndex的时候
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 用分治法递归数列的两部分
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
private static int partition(int[] arr, int startIndex, int endIndex) {
// 坑的位置,初始等于pivot的位置
int index = RandomUtils.nextInt(startIndex, endIndex+1);
System.out.println(index);
// 基准元pivot值
int pivot = arr[index];
int left = startIndex;
int right = endIndex;
// 大循环在左右指针重合或者交错时结束
while (right >= left) {
// right指针从右向左进行比较
while (right >= left) {
if (arr[right] < pivot) {
arr[index] = arr[right];
index = right;
left++;
break;
}
right--;
}
// left指针从左向右进行比较
while (right >= left) {
if (arr[left] > pivot) {
arr[index] = arr[left];
index = left;
right--;
break;
}
left++;
}
}
arr[index] = pivot;
return index;
}
}
上述代码两点需要注意:
- 右指针的元素一旦用来填坑,左指针就右移。
想象下,如果我们选择的基准最初没有与左指针重合,右指针指向元素第一次填坑的时候,左指针如果直接右移会导致什么? 导致序列的最左元素被遗忘,无法参与排序。
- 右指针可以一直左移,直至与左指针重合。
然而,如果我们的基准最初没有与左指针重合,坑在左右指针之间,那么先不说有坑无法移动的事实,如果左右指针同时出现在坑的一侧,会导致什么?
导致乱序 (左指针可以一直右移,因为左指针开始动,右指针肯定至少填过一次)
所以我们需要给代码加限制条件:
- 在右指针元素替换逻辑中,除去left++,即,每次右指针填坑后,左指针不再直接右移,而是进入左指针循环,根据判断条件选择右移
在右指针判断条件增加,right != index ,当右指针与坑重合时不再移动
private static int partition(int[] arr, int startIndex, int endIndex) { // 坑的位置,初始等于pivot的位置 int index = RandomUtils.nextInt(startIndex, endIndex+1); System.out.println(index); // 基准元pivot值 int pivot = arr[index]; int left = startIndex; int right = endIndex; // 大循环在左右指针重合或者交错时结束 while (right >= left) { // right指针从右向左进行比较 while (right >= left && right != index) {//考虑到坑,不能一直左移(不以第一个元素为基准时) if (arr[right] < pivot) { arr[index] = arr[right]; index = right; // left++;//第一次填坑,left指针不一定会直接右移(left!=index,不以第一个元素为基准) break; } right--; } // left指针允许一直右移,因为它遇到坑的时候,一定与right指针重合 // left指针从左向右进行比较 while (right >= left) { if (arr[left] > pivot) { arr[index] = arr[left]; index = left; right--; break; } left++; } } arr[index] = pivot; return index; }我们想一下,其实除了 右指针第一次填坑 ,左指针的右移 需要判断,之后 ,右指针的填坑,左指针都是与坑重合 的,都可以直接进行左指针的右移,所以我们可以优化代码,将 右指针第一次填坑,左指针右移 的逻辑抽取出来,优化后的代码如下: ```java private static int partition(int[] arr, int startIndex, int endIndex) { // 坑的位置,初始等于pivot的位置 int index = RandomUtils.nextInt(startIndex, endIndex+1); System.out.println(index); // 基准元pivot值 int pivot = arr[index]; int left = startIndex; int right = endIndex;
int firstIndex = index; //第一次填坑,left指针不一定会直接右移(left!=index,不以第一个元素为基准) while (right >= left && right != index) {
if (arr[right] < pivot) { arr[index] = arr[right]; index = right; break; } right--;} // 补偿第一次填坑 while (right >= left) {
if (arr[left] > pivot) { arr[index] = arr[left]; index = left; right--; break; } left++;} //如果没有发生填坑,直接返回基准元素的位置,开始下一次分割 if(firstIndex == index)
return index;// 大循环在左右指针重合或者交错时结束 while (right >= left) {
// right指针从右向左进行比较 while (right >= left && right != index) {//考虑到坑,不能一直左移(不以第一个元素为基准时) if (arr[right] < pivot) { arr[index] = arr[right]; index = right; left++; break; } right--; } // left指针允许一直右移,因为它遇到坑的时候,一定与right指针重合 // left指针从左向右进行比较 while (right >= left) { if (arr[left] > pivot) { arr[index] = arr[left]; index = left; right--; break; } left++; }}
arr[index] = pivot; return index;
}
现在,我们知道,<br />1,上述实现,右指针先移动,如果先移动左指针,除了改变两个循环的执行顺序,还要将判断条件对称一下!<br /> 2,坑的位置,即基准的位置并不会影响指针的移动顺序,但是会增加判断条件。<br />·<br />·
<a name="CDGQv"></a>
### 4.2)指针交换法 — 随机选择基准
如果直接按照 **第一个元素为基准的指针交换法** 的实现代码去实现 随机选择基准的快排:
```java
public class QuickSort1 {
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大等于endIndex的时候
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 根据基准元素,分成两部分递归排序
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
private static int partition(int[] arr, int startIndex, int endIndex) {
// 初始pivot的位置
int index = RandomUtils.nextInt(startIndex, endIndex + 1);
int pivot = arr[index];
int left = startIndex;
int right = endIndex;
while (left != right) {
// 控制right指针比较并左移
while (left < right && arr[right] >= pivot) {
right--;
}
// 控制left指针比较并右移
while (left < right && arr[left] <= pivot) {
left++;
}
// 交换left和right指向的元素
if (left < right) {
int p = arr[left];
arr[left] = arr[right];
arr[right] = p;
}
}
// pivot和指针重合点交换
arr[index] = arr[left];
arr[left] = pivot;
return left;
}
public static void main(String[] args) {
int[] arr = new int[]{4, 7, 6, 5, 3, 2, 8, 1, 9};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
}
上述代码中, 随机选择基准 后直接进入 元素移动,先不下结论代码是否正确,我们先来看下,如下这种极端情况。
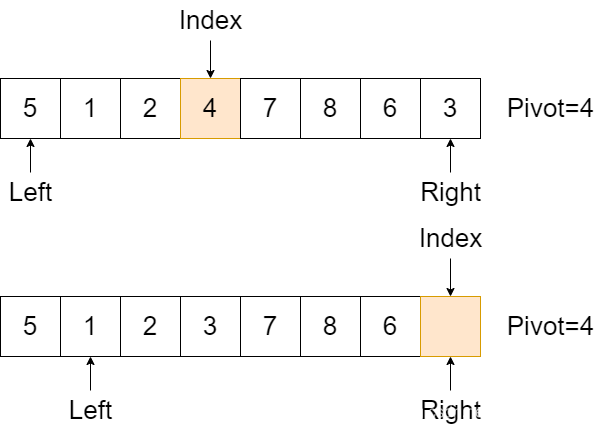
- 初始数列如下,基准元素 4 在最右
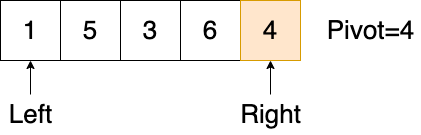
- 依照 元素移动 的规则,无论是Right指针还是Left指针先移动,最终元素交换都是相同的
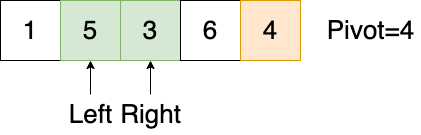
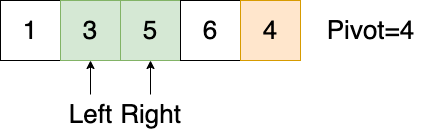
- 但是,当元素交换以后,在下一步,哪个指针先移动,直接影响了与 基准交换 的最终位置。如果Left指针优先移动,最终状态如下,很显然这是我们想要的,一个正确的子排序
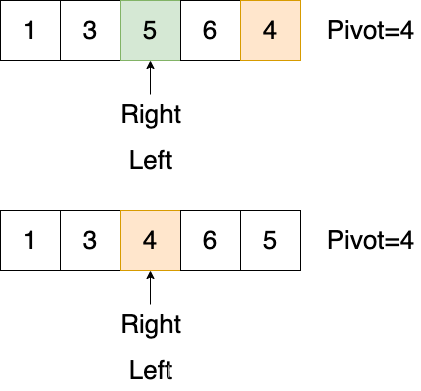
但是,如果Right指针先移动,最终状态如下,显然是错的
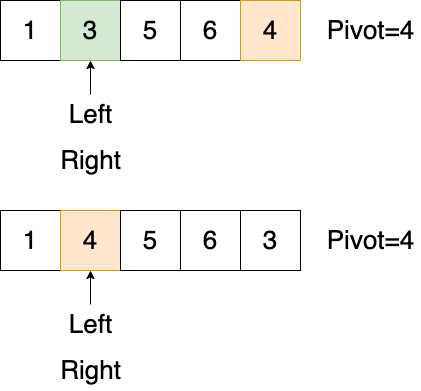
现在,我们知道,当基准位于元素最右,那么Left指针应该优先移动,否则排序失败,同理,当基准位于元素最左(第一个元素),那么Right指针应该优先移动,否则排序失败。
得出结论:
不同于挖坑法,在指针交换法中,基准的位置会影响指针移动的优先顺序。所以,在随机选择基准时,我们要根据基准位置,改变代码执行分支。
毫无疑问代码将变得复杂起来,需要增加额外的判断。
所以,我们 随机基准选择 后往往与 第一元素 交换位置,使处理变得简单起来,代码如下:
private static int partition(int[] arr, int startIndex, int endIndex) {
// 初始pivot的位置
int index = RandomUtils.nextInt(startIndex, endIndex + 1);
// 交换基准位置
int pivot = arr[index];
arr[index] = arr[startIndex];
arr[startIndex] = pivot;
int left = startIndex;
int right = endIndex;
while (left != right) {
// 控制right指针比较并左移
while (left < right && arr[right] >= pivot) {
right--;
}
// 控制left指针比较并右移
while (left < right && arr[left] <= pivot) {
left++;
}
// 交换left和right指向的元素
if (left < right) {
int p = arr[left];
arr[left] = arr[right];
arr[right] = p;
}
}
// pivot和指针重合点交换
arr[startIndex] = arr[left];
arr[left] = pivot;
return left;
}
4.3)总结
通过上述分析,我们知道,当 随机选择基准 时,无论 挖坑法还是指针交换法,都会增加代码复杂度,甚至,循环判断降低了代码性能。
- 挖坑法,增加判断条件
- 指针交换法,影响指针优先移动顺序
不妨,将复杂问题简单化,统一快速排序的过程:
- 选择基准
- 与第一元素交换
- 元素移动
关注作者公众号,随时了解更多干货!