一，红黑树的特点：

  • 第一，结点要么是红色、要么是黑色。
  • 第二，根节点、叶子结点必须是黑色(叶子节点无数据，是空节点NULL)。
  • 第四，红色结点不能连续。
  • 第五，每个红色节点的两个子节点都必须是黑色的。
  • 第六，从任一节点出发，到其每个叶子节点的路径，黑色节点的数量必须相等。

如图为标准的红黑树：

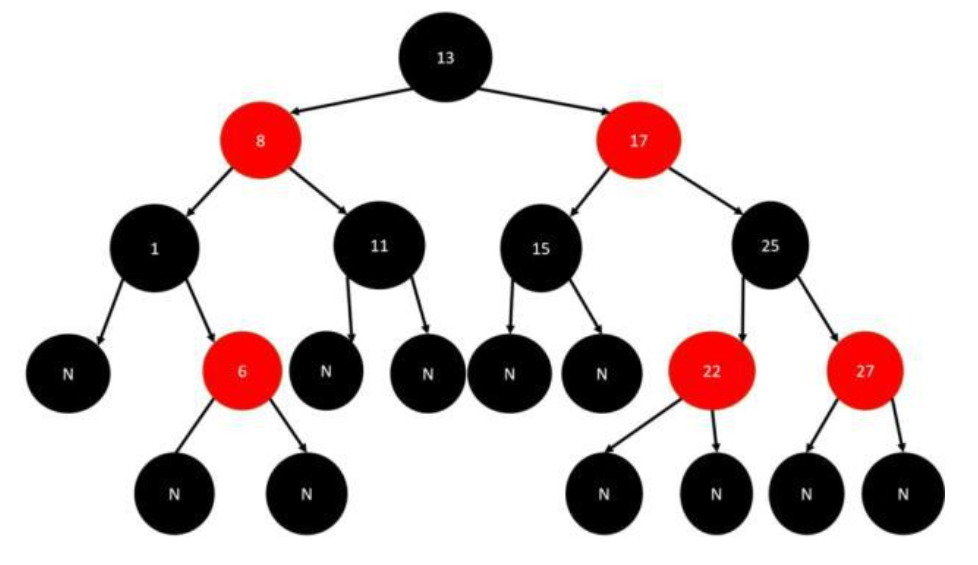
image-20200321111026402.png

二，红黑树的旋转：

1）左旋：

  • 对X节点进行左旋，意味着，将 X 的右孩子（Y节点） **设为** X 的父节点 ；而 X 节点变成了 **它原来的右孩子 的左节点！**
  • 因此，左旋中的“左”，意味着“被旋转的节点将变成一个左节点”。
    如图：

image-20200321111750899.png

eg：
  1.     **将40这个节点左旋，则，40节点的右孩子（60节点） 变成 它的父节点，40节点 变成 它原来的右孩子（60节点）的左节点。**
  3.     **如图：**

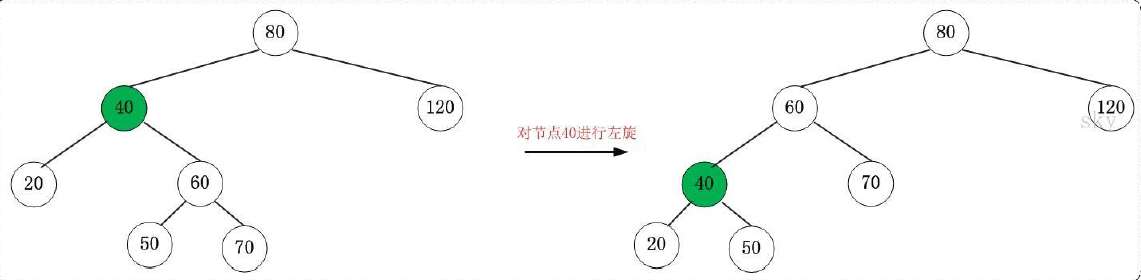
image-20200321112345435.png

2）右旋：

        **对 Y节点 进行右旋，意味着，将 Y节点的左孩子 **`**设为**`** Y的父节点，而 Y节点 变成了 **`**它原来的左孩子的右节点！**`

        **因此，右旋中的“右”，意味着“被旋转的节点将变成一个右节点”。**

如图：

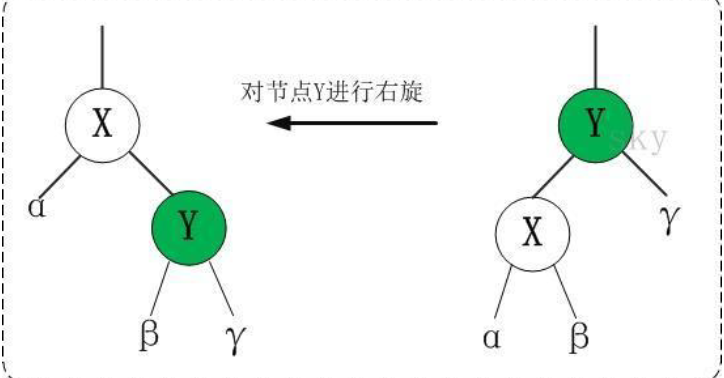
image-20200321113152180.png

eg：
    **对40节点进行右旋，则，40节点的左孩子（60节点） 变成 40的父节点，40节点 变成了它原来的左孩子（60节点）的右孩子。**

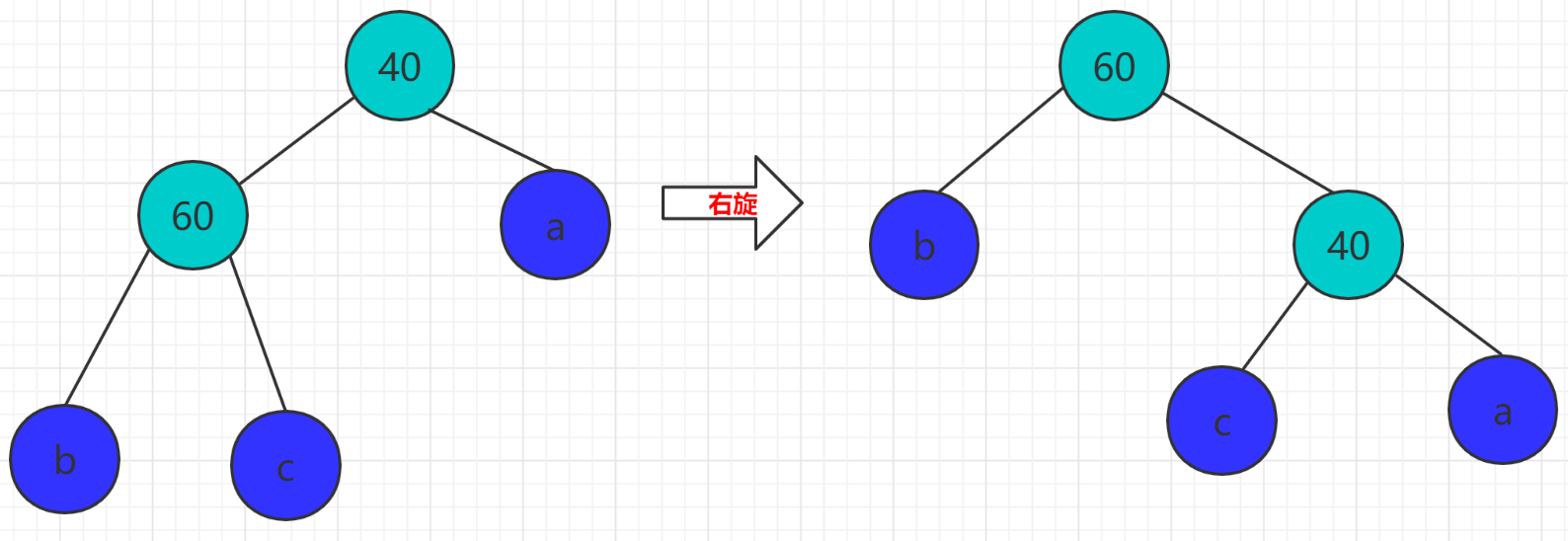
image-20200321115053654.png

三，旋转变色规则：

第一种，当前节点的父节点是红色，且其叔叔节点也是红色，祖父节点不是根节点。

策略：
- （1）将父节点和叔叔节点设为黑色。
- （2）将祖父节点设为红色。
- （3）将祖父节点作为新的当前节点。

第二种，当前节点的父节点是红色，叔叔节点也是红色，且当前节点在最边上（即每行的最左边或最右边的节点），祖父节点是根节点。

策略：

  • 1）将根节点作为新的当前节点，以根节点为支点进行左旋（插入的是右孩子）或者右旋（左孩子）。
  • 2）旋转后将新的根节点变黑色，其他节点根据需要变色，只要保证不出现红红连续节点即可。

  • 3）判断特点6是否已满足，不满足则以当前节点为支点进行一次左旋或右旋，旋转后依旧要保证不出现红红连续节点，否则进行变色。



    第三种，其他所有情况，前提是当前节点的父节点是红色。

策略：

  • 1）将父节点作为新的当前节点。
  • 2）以新的当前节点为支点进行左旋（插入的是右孩子）或者右旋（左孩子）。