统计学笔记
简要大纲
来自《用Python动手学统计学 》
- 统计学
样本:现有数据,总体:现有数据+未知数据
①描述统计:整理、归纳样本
②统计推断:推断总体、未知数据- 只使用样本(总体的一部分)来研究总体
- 抽样过程
①根据随机法则变化的量叫作随机变量
②本书例子中的样本一般认为是通过简单随机抽样从总体中获取的
③样本就是随机变量- 总体有 5 条鱼,样本就是从 5 条鱼中随机选择 1 条的结果
- 不论选择哪条鱼,结果都是随机决定的
- 预测明天的钓鱼结果时,表述为“钓到 2 cm 鱼的概率是 1/5”
- 抽样过程的抽象描述
①概率分布展示了随机变量和它的概率之间的关系
②把抽样理解为从所服从的分布中获取随机变量的过程
③总体服从的分布叫作总体分布
④关于总体- 样本从总体分布中获取
- 描述统计基础
①数据的分类- 定量变量(离散变量、连续变量)、分类变量(名义尺度、顺序尺度)
②频率、频率分布、相对频率分布等整理数据的方法
③直方图数据表示法
④统计量
- 均值:已知数据的代表值- 期望值:未知数据的代表值- 方差:表示数据与均值之间相差多少
- 总体分布的推断
①总体分布以总体的相对频率分布的形式得到- 但是,这个方法必须以普查为前提条件
②直接假设一种总体分布,可以让推断的过程更轻松
- 概率质量函数与概率密度函数
①让总体分布发生变化的量叫作参数
②正态分布有均值和方差这两个参数- 给定均值和方差,通过计算正态分布的概率密度函数,可以得到任意随机变量对应的概率密度
③假设总体分布为正态分布
- 只要估计出正态分布的参数,就能推断出总体分布
- 参数可以直接使用样本的统计量,但此时必须考虑估计误差
- 假设检验(课堂总结)
①参数检验
单样本(paired sample:?例如同一个样本before and after)
两样本(两独立样本)
多样本
②非参数检验
单样本
两样本(两独立样本)
多样本
③对应关系
c1简介与描述性统计
参考书:
带character(‘c’)的是来自《行为科学统计(第七版)》的内容
课程参考书:?
课程:中科院上海生科院2021生物医学统计学(赵兴明)
总体与样本
参数与统计量,取样误差
取样误差是样本统计量和总体参数之间的差异。
描述性统计,推论性统计
这是两个统计技术,它们的一般性目的分别为:简化总结数据,得出一般性结论。
推论性统计为了区分,差异到底是取样误差,还是两组样本间存在真实差异。
数据结构、研究方法与统计
测量每个个体的两个变量:相关法
测量不同的变量
卡方检验
比较两组或多组测量:实验法或非实验法
实验法中有操纵和控制的过程,通过操纵一个变量(自变量)来测量另一个变量(因变量 )。
控制变量:随机,匹配,控制为常量
非实验法/准实验法:自变量虽然不能自己控制了,但是还是用于划分组别。
变量与测量
离散变量、连续变量
连续变量的性质
1.两个不同的个体很少会得到完全一样的值
2.实限:每个测量类别实际上是一个区间,需要用边界定义
称名量表、顺序量表
没有数字时的代替统计技术:中数、众数,斯皮尔曼相关,卡方检验
等距量表、等比量表
统计符号
大写字母一般指的是总体,小写为样本
c2频数分布(描述性统计
将数据整理成图表
频数分布是一种组织好的关于位于测量量表每个类别上的个体数目的数据表
频数f,求和f=个体总和N
比例/百分率p=f/N
累积频数cf
百分位数是和上实限对应(处于或者小于这个区段)
内插法:求已知区间中的未知百分位值,假定为线性变化
茎叶图:融合了表和图的特性,比起直方图,可以展示具体的数值
c3集中趋势(描述性统计
总体平均数希腊字母 ,样本平均数M/
中位数median,众数mode没有用特殊的符号代替
选择一种集中趋势测量
一般选用平均数,因为其使用到了分布中的每个数值,通常具有很好的代表性
使用中位数50%分位数
- 偏态分布skewness、极端数值
- 未确定数值
- 开放性尾端
使用众数
- 称名量表
- 离散变量
- 描述形状
分布形状
正偏态分布:众数-中位数-平均数
c4变异性(描述性统计
变异性提供了对一个分布中的数据分散开或聚集在一起的程度的数量测量
简略测量:全距/四分位距
全距是最大的X值的上实限和最小的X值下实限之间的差值。都为整数的话,为Xmax-Xmin+1。
四分位距是被分布的中间50%覆盖的区域,为Q3-Q1。
标准差和方差
概念
标准差与数据到平均数的平均距离近似,目标是测量标准或典型值到平均数的距离。
Step1: 找出数据的离差,离差带有符号和数值,离差之和为0
Step2:将每个数据的离差平方,然后计算方差
方差=离差的平方的平均数
Step3:标准差=根号下方差
总体到样本:无偏统计量(推论性统计
如果从很多不同的样本中得到样本统计量的平均数等于相应的总体参数值,则一个样本统计量是无偏的。过高或过低的估计,则是有偏误的。因为样本的变化总是小于总体的变化,所以一般是低估的,所以需要矫正。
样本方差矫正样本方差 s的平方=样本的离差的平方和/可以自由变化的数据的个数=SS/df=SS/n-1
对于样本来说,第n个值=nM-前n-1个数的和,所以只有n-1个数据可以自由选择,而对于总体来说,u是未知的。(行为科学统计第7版中文版99-101页)
c5 z分数:分数的位置和标准化分布
把X值转化为z分数的主要目的:1.每个z分布揭示了原始X值在分布内的位置2.z分数构成一个标准化分布,使之能够与其他同样已经转化为z分数的分布相比较
z=
一个靠近0的z分数是靠近中心的,一个在+-2之外的(经验值,处于此概率p=0.0228)z分数是极端的
c6概率/补充内容来自《概率导论》
全概率公式
markdown打公式的方法
贝叶斯公式
P(Ai|B)后验概率,P(B|Ai)先验概率
例题:症状阳性预测值
生统上课提到概念,来源未知:
敏感性 有病检出确实是阳性P(T|D)
特异性 没病检出确实是阴性P(非T|非D)
使用到了贝叶斯公式
症状阳性预测值 症状阳性,得病的概率P(D|T)
一般P(D)、P(T|D)、P(非T|非D)已知,


症状阴性预测值 症状阴性,没得病的概率P(非D|非T)
课程-分布
二项式分布
是一种离散分布
有放回抽样~二项式分布
无放回抽样~超几何分布,样本非常大时(经验性为5%)~二项式分布
二项式分布的统计量



?用来找出概率的是分布之下的面积,要用实限来算吗
极限分布:中心极限定律
q是什么 q=1-p
n->无穷大,p不变,该分布~正态分布:中心极限定律,近似经验值np>=15,nq>=15
以下为二项分布近似为正态分布
平均数:=pn
标准差:
z分数:
n->无穷大,p->0,np不变,该分布~泊松分布,近似经验值n>=100,np<=10
超几何分布

负二项式分布
单细胞测序

泊松分布
是一种离散分布
rna seq常用
参数只需平均值,因此被广泛应用

M=,D=
正态分布
???
c7概率和样本:样本平均数的分布
之前考虑z分数和概率,样本只有一个元素,概念拓展-》
样本平均数转化为z分数,可以用于描述整个样本
建立样本和总体间联系的法则
取样分布
取样分布是一组统计数据的分布,这组统计数据是由从一个总体中取出的所有可能的固定大小的样本得到的。样本平均数的分布是取样分布的一个例子。
1.样本平均数聚集在总体平均数周围
2.全体样本平均数呈正态分布
3.样本越大,样本平均数和总体平均数越近
样本平均数分布:中心极限定律
中心极限定律:对于任意平均数,标准差为
的总体,样本大小为n的样本平均数分布具有平均数
,标准差
,并且当n趋于无穷时,分布将趋于正态。
1.描述任意总体的样本平均数分布,无论什么样形状、平均数或标准差
2.经验值,n=30分布就几乎是正态的
描述统计
样本平均数分布的平均数
集中趋势:M的期望值
M的平均值=
M的期望值定义:样本平均数分布的平均数等于总体平均数,这个平均数被称为M的期望值,即样本分布的平均数“被期望”等于总体平均数。
样本平均数是无偏统计量
变异性:M的标准误(SEM):大数定律
M的标准误定义:样本平均数分布的标准差被称为M的标准误,M的标准误==M和
间的标准距离
?还是不懂公式是怎么来的 标准误=
大数定律:样本大小越大,样本平均数同总体接近的可能性越大
样本越大,其所代表的总体就越准确。因为标准误按照样本的平方根大小递减,所以通过把n增大到30左右来充分减少误差。
标准误与标准差的区别:标准误是样本平均数M到总体平均数
的标准距离,标准差是分数X到总体平均数
的标准距离。每当遇到样本问题时,标准误是对变异性的适当测量。
样本平均数的概率分布:Z分布
z分数=
c8假设检验(推论性统计
c8以后内容为平均数与平均数差异的推论
python https://blog.csdn.net/ws19920726/article/details/105831471
R https://www.cnblogs.com/ywliao/archive/2017/04/17/6724334.html
基本概念
假设检验
假设检验是一种统计方法,它使用样本数据评估关于总体参数的假设。
假设检验有点类似于我们高中数学中常见的“反证法”,即提出一个错误的假设,然后证明它是错的。那么我们提出的假设叫做 原假设/虚无假设 (Null Hypothesis),简写为 。我们备选的假设叫做 备选假设 (Alternative Hypothesis),简写为
或
。注意,在假设检验中只有 2 个假设,即原假设和备选假设,我们的目的就是要拒绝原假设。
处理效应
基本假设:如果某个处理有效应,那么这个效应只是在某个分数上+/-一个常数,会改变平均数,但是不会改变总体的分布情况和标准差。
测量效应的大小:科恩d值
?类似于z分数
测量了两个分布之间分开的程度
(待补充)统计效能
统计检验效能是检验能够正确地拒绝错误的虚无假设的概率,效能是检验能够识别真正存在的处理效应的概率。
同样可以通过看分布图像算概率,可以在研究前确定出现显著效应(拒绝)的概率。
书中例子:
两者关系
假设检验评估了处理效应的相对大小(相对于随机性的结果)而不是绝对大小。
假设检验的流程:
1.作出关于总体参数的假设->未知总体(是个媒介,其实这个总体并不存在)#可以回去看p195的图
在假设检验过程中,我们一般设定原假设和备选假设 如下,
原假设:两组数据没有显著性差异
备选假设:两组数据存在显著性差异
2.使用假设预测样本统计量,注意取样误差的存在
显著水平是一个概率值,虚无假设是正确的情况下非常不可能出现的样本结果/ 在临界区域上的概率
临界区域虚无假设是正确的情况下非常不可能出现的样本值组成的区域,由显著水平决定,如果样本处于临界区域中,则拒绝虚无假设
3.从总体中随机抽样
4.比较样本数据和总体假设
进一步讨论z分数
z分数==
M越大,越小,n越大,z越大
假设检验需要检验统计比足够大,以满足基于显著水平的判断标准,显著水平为0.05或0.01时,通常意味着比例在2-3之间。
使用z检验的情况
样本随机抽取,两个观察间相互独立,服从正态分布,总体均值已知,总体方差已知
(来源于处理效应的基本假设),通过算z分数判断是否处于临界区域中。
假定的原因
样本随机抽取:样本能够代表总体
两个观察间相互独立:效应能够归纳到总体
处理没有改变总体的标准差:在假设检验中处理后的样本来自处理后的未知总体,所以假定处理后的总体标准差不变。
实际上这个假定是一个更普遍的假定产生的结果,它是统计过程的一部分,这个普遍的假定陈述了处理效应是对总体的每个分数加上或减去一个常数量,这将改变平均数,但是不影响标准差。(这是一个理论上的假定)
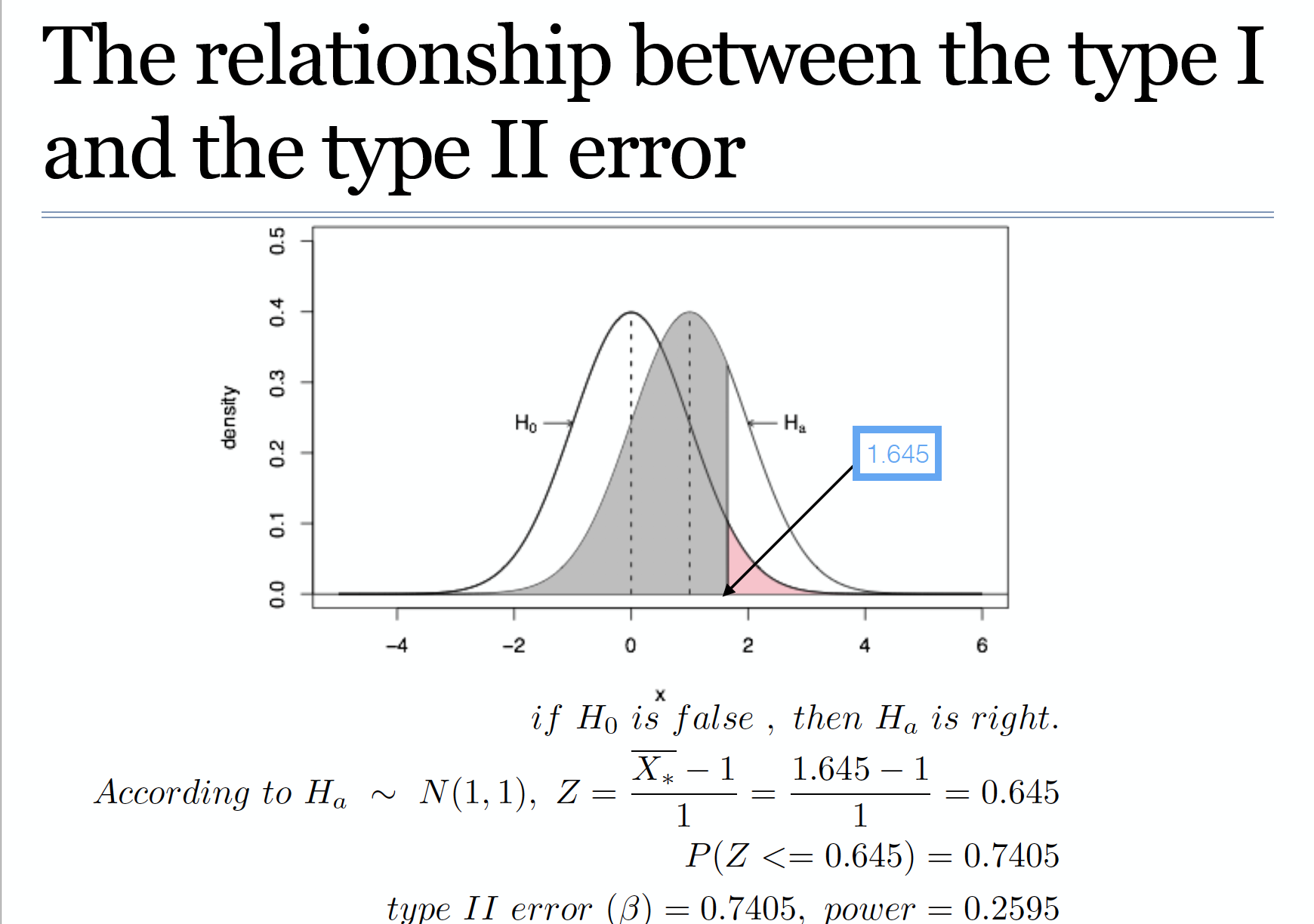
假设检验的不确定性和误差:第一类误差
拒绝虚无假设时出现:
第一类误差:研究者在虚无假设正确的情况下拒绝虚无假设(没有处理效应的时候得到了有处理效应的结论)。
第一类误差出现在处于临界区域的极端样本,所以显著水平定义了出现第一类误差的概率。
接受虚无假设时出现:
第二类误差:研究者不能拒绝一个错误的虚无假设(假设检验不能检测出真正的处理效应)。由概率表示。
第二类误差出现在当处理对样本有效应,但样本平均数不在临界区域上时。这种情况时常发生在处理效应相对较少的情况下。
| 实验者结论\真实情况 | 没有效应, 是正确的 |
有效应, 是错误的 |
|---|---|---|
| 支持 | 结论正确 | 二类误差 |
| 拒绝 | 一类误差 | 结论正确,统计检验效能 |
第一类误差出现的概率=显著性水平
第二类误差的不出现的概率=统计效能
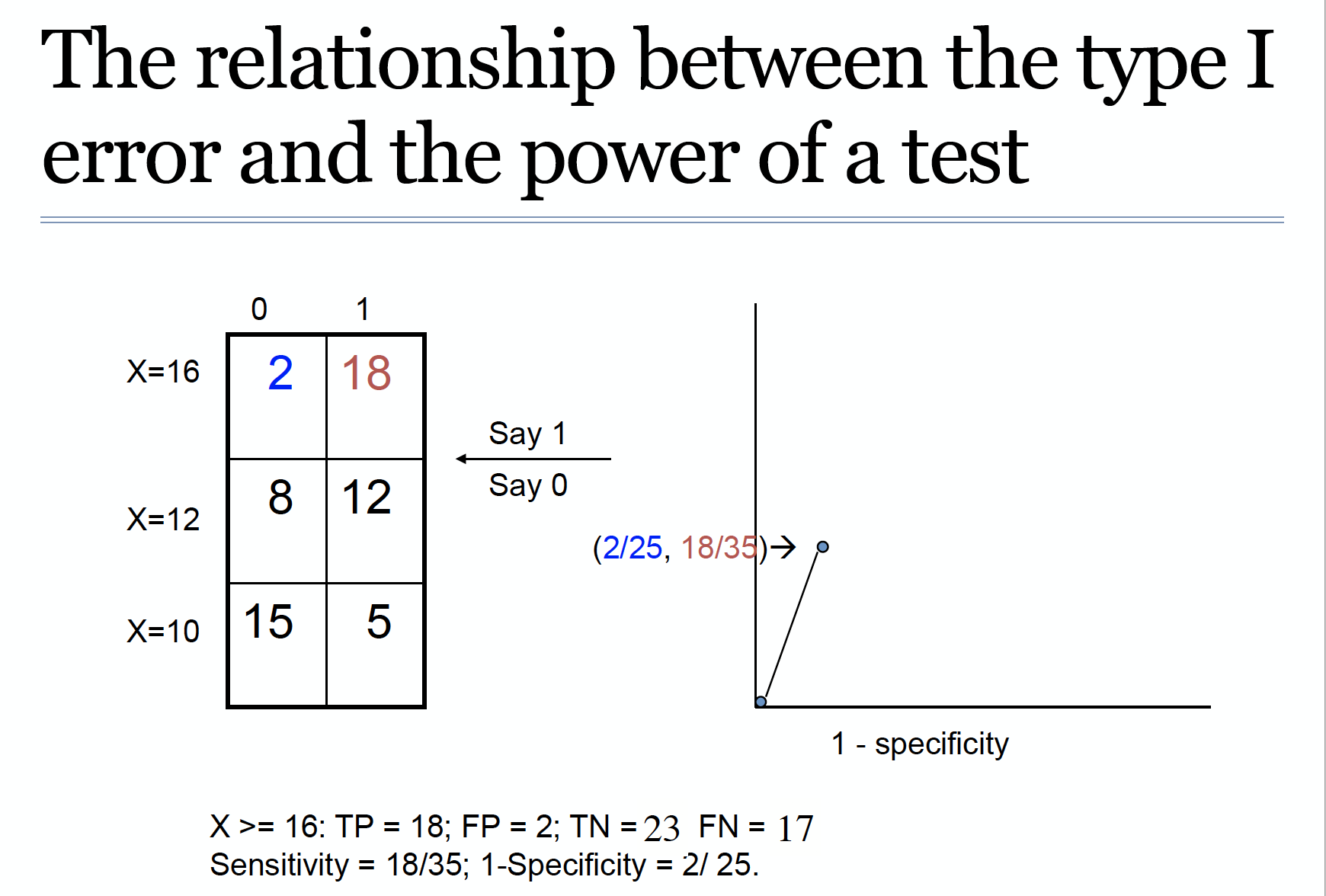
ROC曲线
统计效能
估计样本容量
假设检验的例子
实际情况: 原始总体->样本-》处理-》处理后的样本
假设检验:原始总体-》处理-》处理后的总体->处理后的样本
方向性(单尾)假设检验
在方向性假设检验,或单尾检验中,统计假设规定了总体平均数的增加或减少,即它们作出关于效应方向的陈述。
两样本时:需要方差相同,先做f检验
多假设检验矫正
出现第一类误差的概率p=
bonferroni矫正
顺序矫正
FDR
可能需要花时间听他2.3次的网课
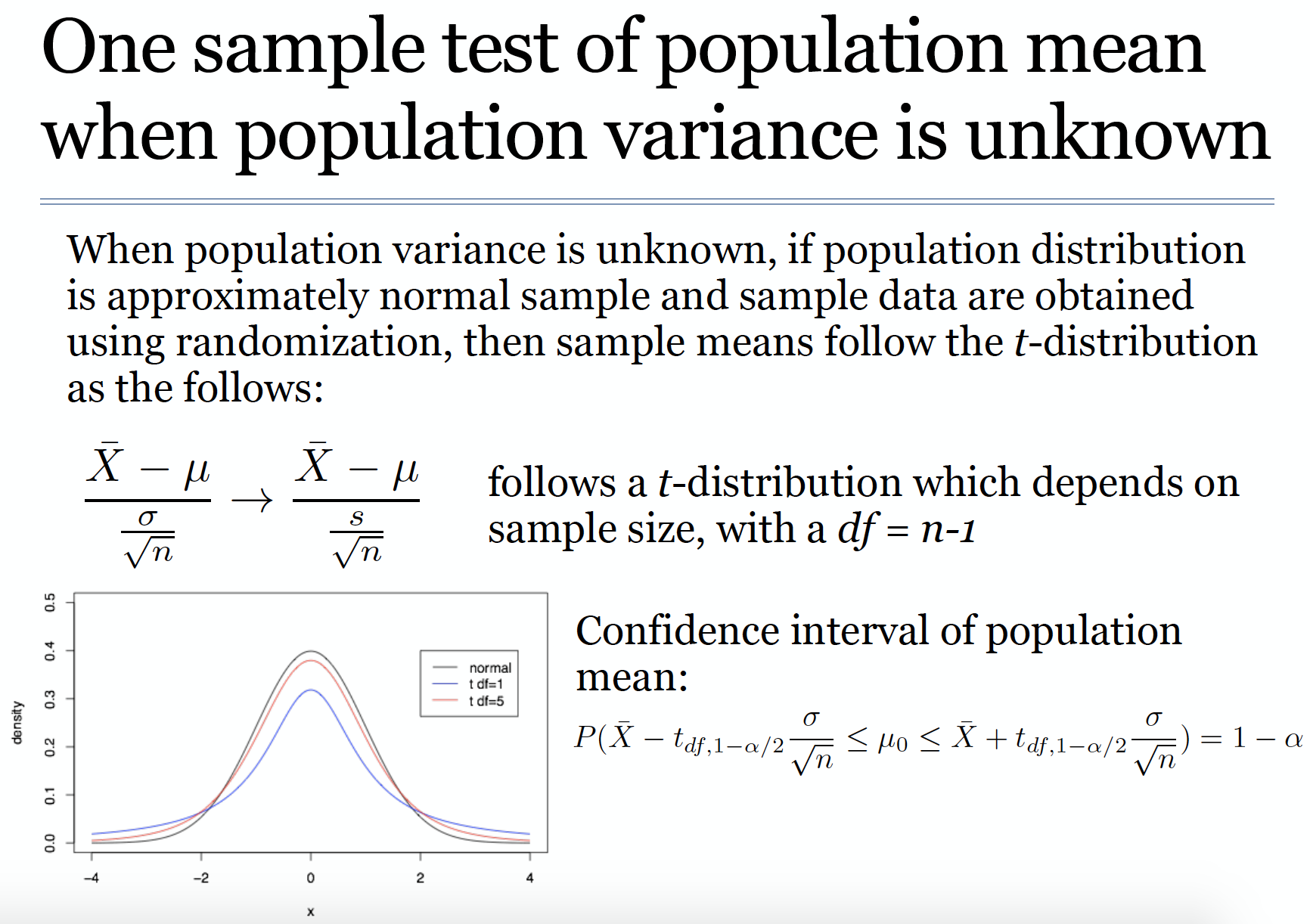
c9 t分数
方差未知的时候,使用样本标准差代替总体标准差。和z分数的公式相比,只是将总体标准误变为了样本标准误。
c12估计(推论性统计-也可以用于假设检验
用样本统计量推断总体参数的推论性过程被称为估计。样本和总体之间存在的差异被称为取样误差。
点估计和区间估计
点估计是使用单一的数值作为对未知量的估计。
区间估计使用值域对未知量进行估计,伴随着一定的水平的信心(或可能性),称为置信区间。
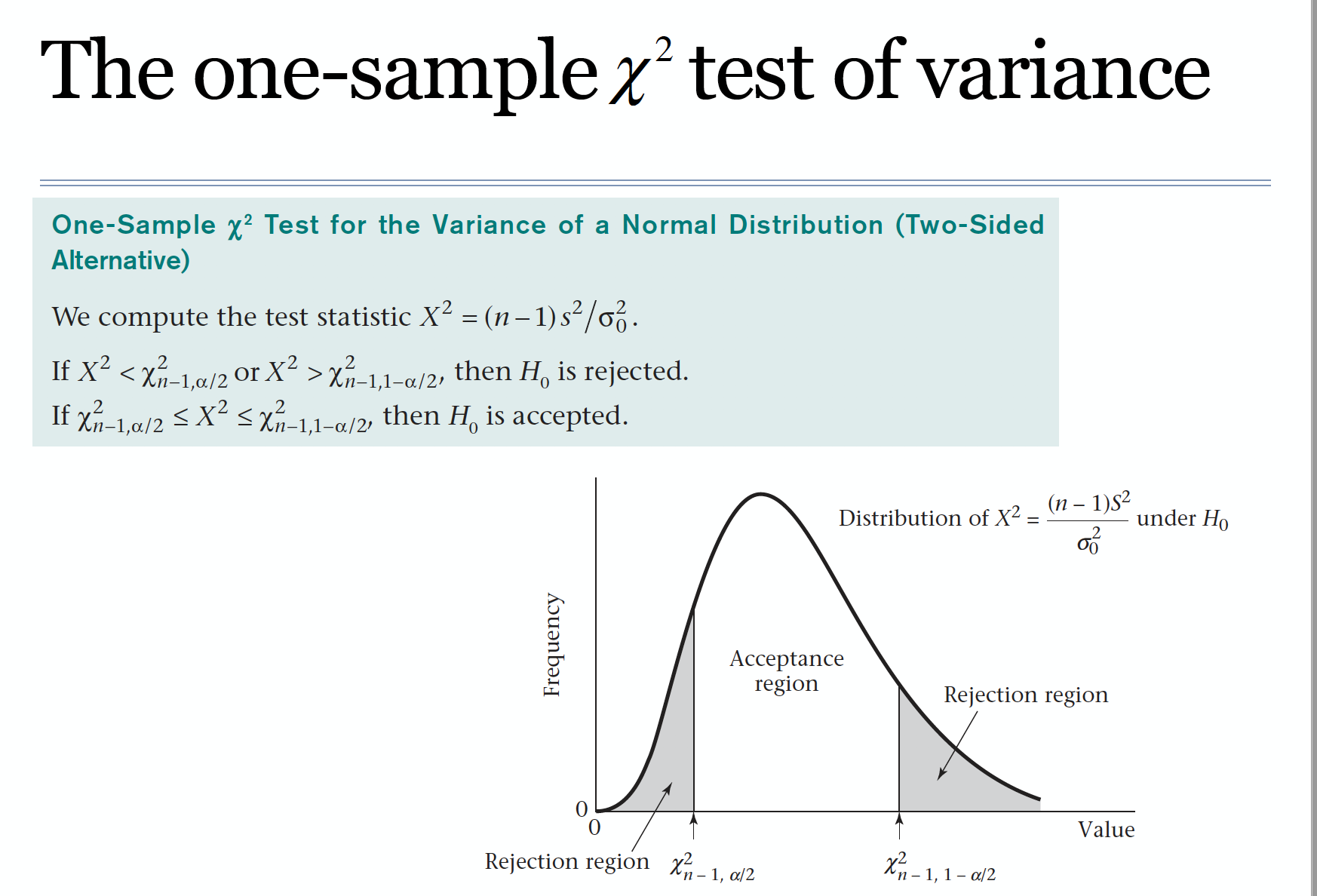
c13方差分析
卡方分布
多样本假设检验
多假设检验校正
family-wise error rate
wilcoxon检验
1.Wilcoxon rank-sum test 威尔科克森秩和检验
基本概念: 在统计学中,Wilcoxon rank-sum test(威尔科克森秩和检验)也叫 Mann-Whitney U test(曼-惠特尼 U 检验),或者 Wilcoxon-Mann-Whitney test。秩和检验是一个非参的假设检验方法,一般用来检测 2 个数据集是否来自于相同分布的总体。
2.Wilcoxon signed-rank test 威尔科克森符号秩检验
基本概念: Wilcoxon signed-rank test(威尔科克森符号秩检验)也是一种非参的假设检验方法,它成对的检查 2 个数据集中的数据(即 paired difference test)来判断 2 个数据集是否来自相同分布的总体。
卡方检验 卡方值
列联表的属性的独立性检验
数据分析有一个很简单的标准,只要列联表中存在不足5 的频数,就要尽量避免使用卡方检验
回归及关联分析
一元线性回归
从oneway anova到线性回归
例子:钠肥的用量和叶片重量的关系,散点图拟合回归线
画出一个向上趋势的回归线,~没有重复实验的anova分析
重复后画出线性回归线,~有重复实验的oneway anova分析
例子:孕妇雌激素含量和婴儿体重的关系
是否有影响?oneway anova
什么关系?线性回归
oneway anova
Full linear regression model y=a+bx+e,b回归系数
残差 实际的y与预测y间的距离
残差平方和
最小二乘法 当残差-》L最小拟合效果越好,所以对L求偏导可将a,b化为
需要注意⚠️:别的数据使用模型时,需要注意训练模型的数据范围
假设
H0:回归系数等于0
相关系数
协方差/两者标准差,检查两组数据间的离散程度是否一致,x-bar(x)& y-bar(y)形成的夹角的余弦值
多元线性回归
协变量
y=a+sum bx+e,b部分回归系数
例子:家庭生育小孩数目与家庭收入和家庭教育水平的关系
作出假设检验两个不相互影响的假设
两个变量拟合出来的是一个平面
例子:血压与年龄和出生体重的关系
哪个变量更重要?
标准回归系数,summary中可以显示算出的
当x->x+
,y->y+
,标准化后为y->y+
,S为标准差
所有变量拟合效果F 检验
探究不同变量的效果t-tet/部分f-test

使用的注意事项⚠️:
1.处理数据时考虑是否要去掉离群值
2.?mask effect 一个变量可以预测另一个变量,可能这个变量会把另一个变量的效果完全掩盖
3.collinear effect 两个变量间有线性关系
例子:谋杀犯罪率与当地人口数目,文盲,收入水平,气温
cor(data) 看相关关系
anova(reduced model, full model) 看去掉一些“不重要的变量”后拟合的差异(证明是真的不重要,二次伤害
例子:房价的影响因素
常见的非线性回归模型:逻辑回归
使用情况:
1.x可以是离散变量或者是连续变量,去预测一个离散变量y
2.x不一定要正态分布、方差相同
3.非线性关系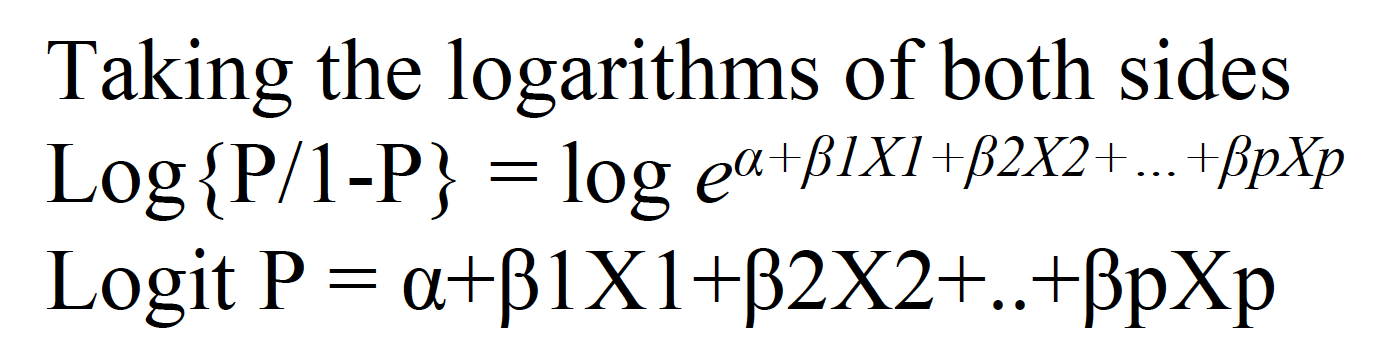
b回归系数的影响比截距a大
例子:足球输赢与难度、赛季的关系
b回归系数显著性 wald-test(z-test)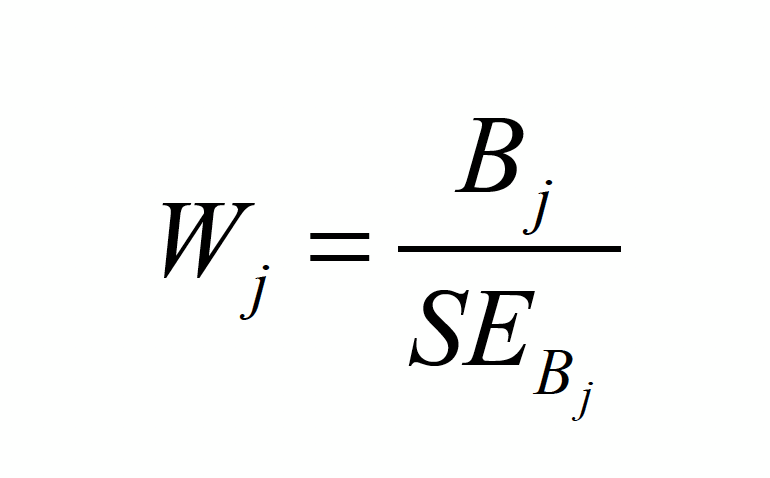
例子:婚外情的影响因素
逻辑回归使用的是glm general linear model
1.将y变成逻辑变量
2.glm full model
3.glm reduced model 可以影响实验设计
4.回归系数指数化变回原始模型
5.可以将其他变量指定为平均值,探究单个变量的概率
部分相关及多元相关/条件回归
可以探究因果关系
一般会比之前的算相关的方法得到的相关系数小
例子:谋杀犯罪率与当地人口数目,文盲,收入水平,气温
皮尔森相关系数
cor(y,b1x1+b2x2+b3x3+bkxk)->算的是R方
基因表达分析
micro-array
RNAseq
需要研究的基因给定score
方法一:fold change
常用阈值:2倍变化
问题:
1.原先表达值过大或者过小时都容易漏掉数据
2.没有考虑方差
方法二:statistic test
两样本参数假设检验p-value找差异表达基因
t-test
ANOVA
非参数检验 wilcoxon rank test
富集分析
fisher‘s test
超几何检验的特殊形式
主成分分析
PCA 的思想很简单——减少数据集的变量数量,同时保留尽可能多的信息
https://builtin.com/data-science/step-step-explanation-principal-component-analysis
原先的变量间有一定的相关性
相当于对原先变量做线性变换,找原先变量的方差和协方差的主成分:主成分是由初始变量的线性组合或混合构成的新变量。这些组合以这样一种方式完成,即新变量(即主成分)不相关,并且初始变量中的大部分信息被挤压或压缩到第一成分中。所以,这个想法是 10 维数据给你 10 个主成分,但 PCA 试图将最大可能的信息放在第一个组件中,然后在第二个组件中放置最大的剩余信息,依此类推。这里要意识到的重要一点是,主成分的可解释性较差并且没有任何实际意义,因为它们被构造为初始变量的线性组合。从几何上讲,主成分表示解释最大方差量的数据的方向, 也就是说,捕获数据的大部分信息的线。这里的方差和信息的关系是,一条线携带的方差越大,沿线数据点的离散度就越大,沿线的离散度越大,它所包含的信息就越多。简而言之,只需将主成分视为提供查看和评估数据的最佳角度的新轴,以便更好地观察观察之间的差异。
生物中主要用于降维,找到保留原先关系的最小子空间,变量间相互正交
第一主成分必须捕捉到原始数据中最大的方差
第一主成分示意图
第二主成分必须与第一主成分正交,捕捉到原始数据中次大的方差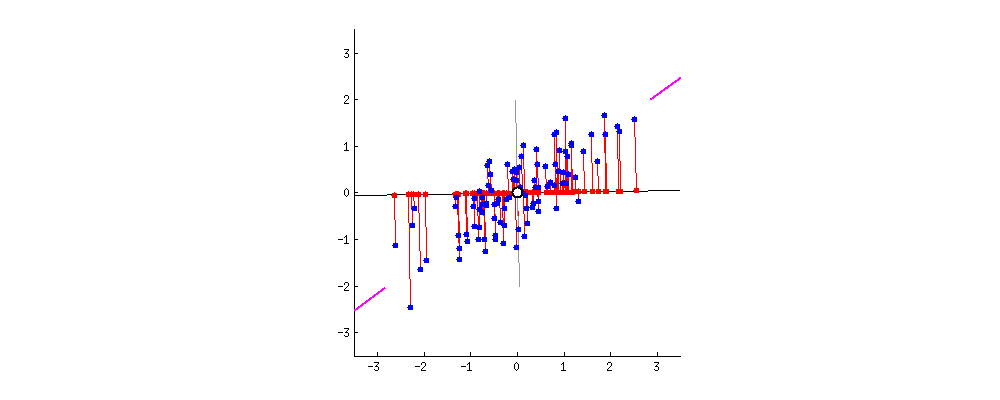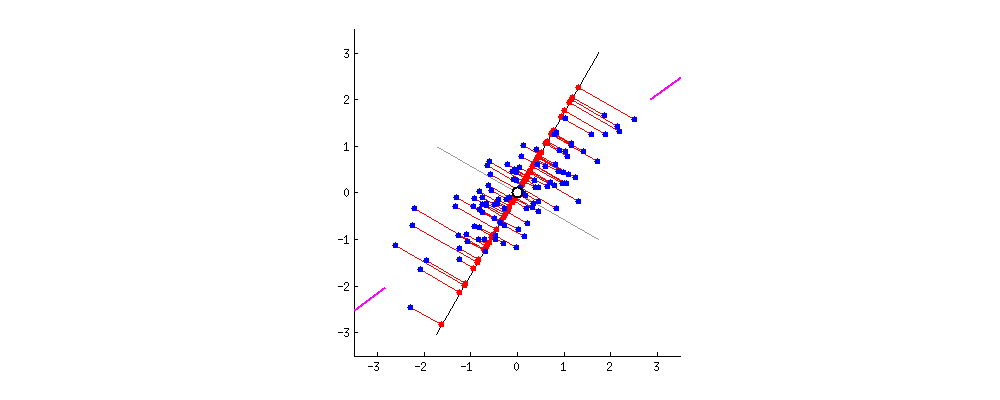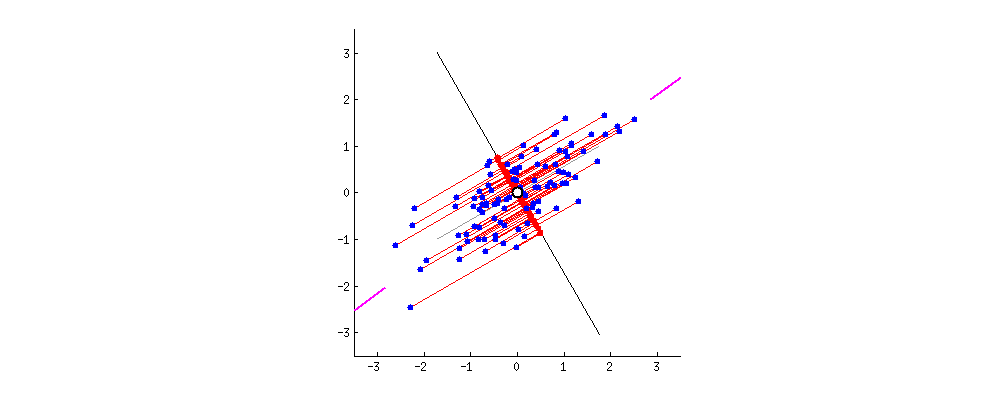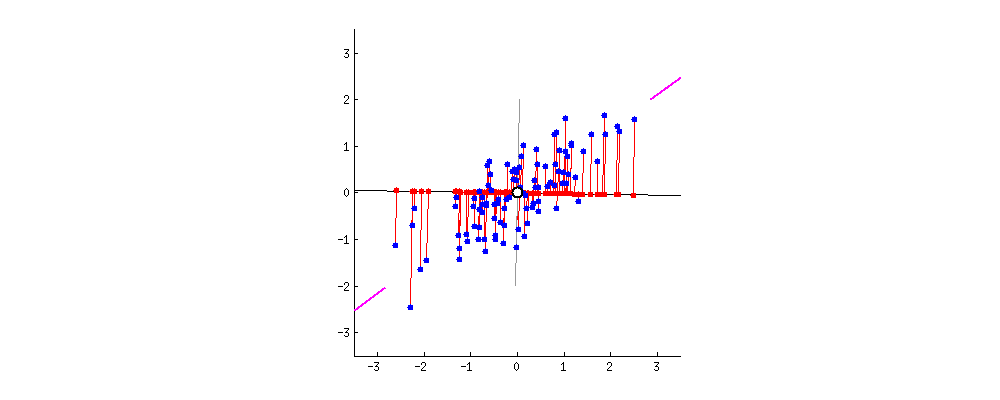
例子:Given 53 blood and urine samples (features) from 65 people(33 alcoholics, 32 non-alcoholics).
步骤:
1.标准化:两个变量间的协方差~19:计算之前变量需要是相同单位的,所以可以先对变量做中心标准化,即求z分数。完成标准化之后,协方差就变成了两个变量间的相关系数~29
2.协方差矩阵计算:此步骤的目的是了解输入数据集的变量如何相对于彼此的均值而变化,或者换句话说,查看它们之间是否存在任何关系。因为有时,变量以包含冗余信息的方式高度相关。因此,为了识别这些相关性,我们计算协方差矩阵。
S叉乘矩阵 方差(对角线)-协方差矩阵 S=X’X
|标准化
相关系数矩阵(对角线为1)
3.?特征向量是什么
计算协方差矩阵的特征向量和特征值以识别主成分:因为协方差矩阵的特征向量实际上 是方差最大(信息最多)的轴的方向,我们称之为主成分。特征值只是附加到特征向量的系数,它给出了 每个 Principal Component 中携带的方差量。
求特征值lamda
|S-lamda I|=0,trace 方差,lamda /trace 该成分占方差的比例(解释力)
成分矩阵
4.沿主成分轴重铸数据
目的是使用协方差矩阵的特征向量形成的特征向量,将数据从原始轴重新定向到由主成分表示的轴(因此称为主成分分析) )。这可以通过将原始数据集的转置乘以特征向量的转置来完成。
奇异值分解SVD
应用:人脸识别,图片识别,噪声过滤
r~83,85
聚类
最小化聚类内部的距离,最大化聚类间的距离
聚类中的度量
1.实数变量
距离
相似度:相关系数
2.二元变量
3.类别变量
4.序数变量
5.余弦度量
方法分类
– 划分聚类方法
k-means
Step 1:确定聚类数目k
Step 2:将样本随机划分到k簇中,并计算k簇的
中心(均值),并以这些中心作为新的基石或种
子(原来的“种子”就没用了),重新按照距离
分类
Step 3:如此叠代下去,直到达到停止叠代的要
求(比如,各类最后变化不大了,或者叠代次数
太多了)
– 层次聚类方法
agnes算法 基因聚类
diana算法
– 密度聚类方法
– 网格聚类方法
– 基于模型的方法
– 其它聚类方法
生存分析
生存函数
风险函数hazard function
3个生存方法:参数法,半参数法,非参数法
与回归的不同点:
1.对时间(某个事件发生到目前为止的时间)建模
2.生存分析为二值事件(生或死)
3.数据有删失,截尾
4.比较两个或多个群体
censoring删失,截尾
做生存分析会将删失数据纳入分析,即试验期内尚未观测到结果,或者中途被试退出的数据
分布函数f(t)~19
生存函数1-f(t)
风险函数h(t)=f(t)/s(t)【贝叶斯定理
其他公式~27
分布近似Introduction to Kaplan-Meier
1.指数函数
此时风险函数为常数,例如机器使用年限等问题
2.weibull函数
方法:
1.参数法~46
log h(t)=
2.半参数法cox model
h1(t)/h2(t) 看倍数
3.非参数Kaplan-Meier model(乘积极限法)
例子:带有截尾、删失数据(right-censored)
删失前*删失后去估计删失处的生存值