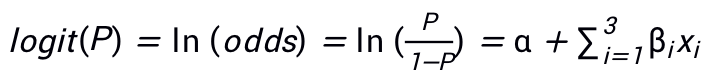生物统计学上课内容整理而成,主要参考《R语言实战》
常用操作
?/help()帮助
q退出查看帮助文档
ls()查看当前变量
rm(name)删除单个变量
rm(list = ls())清除所有变量(到回收站
gc()完全删除
dir()查看当前目录下文件和目录
getwd() 当前目录
setwd() 设置操作目录
数据objects
index从1开始【py从0开始】
查看数据类型class()
查看数据模式 mode() :numeric,complex,logical
logical表述方式是全大写TRUE/ FALSE
呈现方式可以给行/列赋名称,名称可用于索引,有点类似生成Excel表格

向量vector
r中没有标量,都是按向量形式储存
不同长度的向量进行运算时,操作循环补齐
创建与合并 c()
索引与切片 a[1:n],a[-2]代表的是不选择这个下标【py中指的是从后开始数】,两个不连续的element索引时要用c(),a[c(1,3)]
矩阵matrix
matrix(c(),nrow=指定行数,byrow=TRUE默认按列排列可以改为按行)
呈现方式可以给行/列赋名称,名称可用于索引
> rnames = c('math','bio')> cnames = c('bob','tom','may')> score[,1] [,2] [,3][1,] 100 94 80[2,] 95 96 83> score = matrix(c(100,95,94,96,80,83),nrow = 2,dimnames = list(rnames,cnames))> scorebob tom maymath 100 94 80bio 95 96 83> score['math',]bob tom may100 94 80
矩阵乘法是 a%%a 【aa对应元素两两相乘】
矩阵转置 t()
矩阵求逆 solve()
array
另一种matrix
数据框Data.frame
另一种matrix
类似于excel表格,将不同的数据类型信息保存到data.frame结构中,所以也可以直接导入excel
一般来说每行代表一个样本,每列代表一个变量
调入数据集 data()
查看数据集前几行 head(x, n=6默认)/ 后几行tail()
查看行列数dim()
行数nrow()
列数ncol()
索引~通过列名索引列
1.frame$column
2..attach(frame)-> list out all column names-> enter column name<br />索引~行<br />frame[rownum,colnnum]
查看与修改列名 names() names() = c()
order()排序
data3$sumnorm <- apply(data3[,1:3],1,sum)
data3$sumtumor <- apply(data3[,4:6],1,sum)
row.names(data3)[order(data3$sumnorm,decreasing = T)[1]]
# "7223"
row.names(data3)[order(data3$sumtumor,decreasing = T)[1]]
# "652991"
列表list
【像py中的字典】
l = list(name='', age='', is_good=TRUE)
索引
1.l$name
2.l[[2]]
3.l[['name']]
数据集的操作
取子集
subset()
which() 取出符合某个条件的子集
#不表达的基因(数据=0),行为样本编号14个*列为基因199个
#subset()
> A9QA = gene[8,]#取出需要分析的样本行
> A9QAmis = subset(A9QA, A9QA==0)
> View(A9QAmis)
#which()
colnames(data[,which(data['A9QA',]==0)])
names(data['A9QA',which(data['A9QA',]==0)])
取交集
随机抽样
抽样 sample()
重复随机抽样的过程 replicate()
# sample()
> genesamle = gene[sample(1:ncol(gene),10,replace=FALSE)]#replace参数有无放回抽样
>choujiang <- c("未中奖","一等奖")
# replicate()
> replicate(7,sample(choujiang,100,prob = c(99,1),replace = TRUE))
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖"
[2,] "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖"
[3,] "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖"
[4,] "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖"
[5,] "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖" "未中奖"
导入数据及文件读写
【像matlab设置路径】
当前目录 getwd()
使用r 中预置的数据
states = as.data.frame(state.x77[,c(‘murder’,’illteracy’,’income’,’frost’)]
缺失值
缺失值以符号NA(Not Available,不可用)表示。不可能出现的值(例如,被0除的结果)通过符号NaN(Not a Number,非数值)来表示。
判断向量内每个元素是否为NA is.na()
其中,is.na用于判断向量内的元素是否为NA,返回结果是和原向量大小相同的一个向量:c(FALSE FALSE FALSE TRUE TRUE FALSE TRUE FALSE)
即x内元素为NA,其对应的下标元素是TRUE,反之是FALSE。!x是取非逻辑运算符,!is.na(x)表示a内元素不为NA,其对应的下标元素是TRUE,反之是FALSE。通过x[!is.na(x)]进行索引后,即可取出a内不为NA的元素,将其过滤。
mystats = function(x, na.omit = FALSE){
if (na.omit)#if在没有{}的情况下只执行后面一句
x = x[!is.na(x)]#取出x中不为na的值
...
}
⚠️注意:缺失值被认为是不可比较的,即便是与缺失值自身的比较。这意味着无法使用比较运算符来检测缺失值是否存在。例如,逻辑测试myvar == NA的结果永远不会为TRUE。作为替代,你只能使用处理缺失值的函数(如本节中所述的那些)来识别出R数据对象中的缺失值。
和py不同,py大部分情况可以使用==,在NaN上不行
重编码某些值为缺失值 x[x$age == 99] = NA
部分函数的参数中有na.rm=TRUE 在计算前移除缺失值,并用剩余值进行计算
删除所有含有缺失数据的行 na.omit()
more in 15章
运行脚本及输出
单处理 ?文本和图像不能一起输出吗
运行脚本source(‘path/filename.R’)
文本输出sink(‘savefilename’),使用参数append=TRUE可以将文本追加到文件后,而不是覆盖它。
参数split=TRUE可将输出同时发送到屏幕和输出文件中
图形输出pdf(‘savefilename.pdf’)/ png(“filename.png”),最后使用dev.off()将输出返回到终端
批处理
终端R CMD BATCH options infile outfile
其中infile是包含了要执行的R代码所在文件的文件名,outfile是接收输出文件的文件名,options部分则列出了控制执行细节的选项。依照惯例,infile的扩展名是.R,outfile的扩展名为.Rout
使用鼠标选择文件
data = read.table(file.choose())
使用键盘输入数据
mydata = data.frame(age=numeric(0), gender=character())
mydata = edit(mydata)
读入csv文件
*csv是逗号分割的文件所以sep为,分隔符 \t换行符
读入表格 mydata = read.table(‘../ants.csv’,header=TRUE表头,sep=’,’分隔符)
table() 可以生成列联表
colClasses指定列的数据类型menus <- read.csv(“menus.csv”, stringsAsFactors = FALSE, colClasses = c(“factor”, “Date”, “numeric”))
描述性统计
基本信息
均值mean()标准差 sd()
4分位数极值均值summaty()
偏度峰度 使用包
> summary(iris$Sepal.Length)
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.300 5.100 5.800 5.843 6.400 7.900
查看概括信息 行列数据类型str(), 4分位数极值均值summaty()
默认描述不带算标准差,可以通过循环来算
#方法一:循环遍历
> genesd = c(1:199)
> for (i in 1:199) genesd[i] = sd(gene[,i])
> genesd
#方法二:使用apply()
> statistic<-apply(data,2,function(x){
+ Mean<-mean(x);names(Mean)<-"Mean"
+ Sd<-sd(x);names(Sd)<-"Sd"
+ Max<-max(x);names(Max)<-"Max"
+ return(c(Mean,Sd,Max))
+ })
>statistic
#方法三:sapply()+定义函数(来自R语言实战)
> vars = c('Sepal.Length')
#na.omit返回剔除了缺失值的对象,希望保留原数据的个数
> mystats = function(x, na.omit = FALSE){
if (na.omit)#if在没有{}的情况下只执行后面一句
x = x[!is.na(x)]#取出x中不为na的值
m = mean(x)
n = length(x)
s = sd(x)
skew = sum((x-m)^3/s^3)/n
kurt = sum((x-m)^4/s^4)/n-3
return(c(n=n, mean=m,stdev=s,skew=skew,kurtosis=kurt))
}
> sapply(iris[vars], mystats)
Sepal.Length
n 150.0000000
mean 5.8433333
stdev 0.8280661
skew 0.3086407
kurtosis -0.6058125
is.na()
其中,is.na用于判断向量内的元素是否为NA,返回结果是和原向量大小相同的一个向量:c(FALSE FALSE FALSE TRUE TRUE FALSE TRUE FALSE)
即x内元素为NA,其对应的下标元素是TRUE,反之是FALSE。!x是取非逻辑运算符,!is.na(x)表示a内元素不为NA,其对应的下标元素是TRUE,反之是FALSE。通过x[!is.na(x)]进行索引后,即可取出a内不为NA的元素,将其过滤。
使用apply()函数
apply(X, MARGIN1:rows2:cols, FUN{}, …)
使用包
Hmisc包中的describe()函数可返回变量和观测的数量、缺失值和唯一值的数目、平均值、分位数,以及五个最大的值和五个最小的值。
pastecs包中stat.desc()其中的x是一个数据框或时间序列。若basic=TRUE(默认值),则计算其中所有值、空值、缺失值的数量,以及最小值、最大值、值域,还有总和。若desc=TRUE(同样也是默认值),则计算中位数、平均数、平均数的标准误、平均数置信度为95%的置信区间、方差、标准差以及变异系数。最后,若norm=TRUE(不是默认的),则返回正态分布统计量,包括偏度和峰度(以及它们的统计显著程度)和Shapiro–Wilk正态检验结果。这里使用了p值来计算平均数的置信区间(默认置信度为0.95).
psych包describe()函数计算非缺失值的数量、平均数、标准差、中位数、截尾君之、绝对中位差、最小值、最大值、值域、偏度、峰度、平均值的标准误。
概率分布
pnorm(zscore) 根据z分数求概率
qnorm(p) 根据概率求z分位数,例如置信区间为95%时:qnorm(0.975)=1.9599~1.96
例题:_
泊松分布

5. 从 1000 米布匹中随机抽取 3 米进行检验,若 3 米中无瑕疵才可接受,假设送检布匹平均每米有一个瑕疵,则被拒收的概率是多少?
基本作图
划分画图区域
par(mfrow=c(2,2)) 将画图区域划分为2x2的格子
直方图
hist(data,breaks=:),breaks为坐标轴上的标注
>hist(res, breaks = 0:18)
箱线图
> boxplot(iris$Sepal.Length, main='Box plot', ylab='Sepal length')
#得到其中具体的统计值
>boxplot.stats(iris$Sepal.Length)
#outline去除离群值
> boxplot(t(genesamle), outline=FALSE)
样本正态性检验
shapiro.test(data)
检验的原假设为,H0:样本服从正态分布
p>0.05,不拒绝原假设,样本服从正态分布。
对于value~factor的数据,对每一个factor做正态性检验data: dat[which(dat$seed == 1), 1]
qq plot
qqplot 要求用lm()拟合,看数据是否落在95%CI内
qqPlot(lm(response~trt, data=cholestero1),aimulate = T, main=’qq plot’, labels = F)
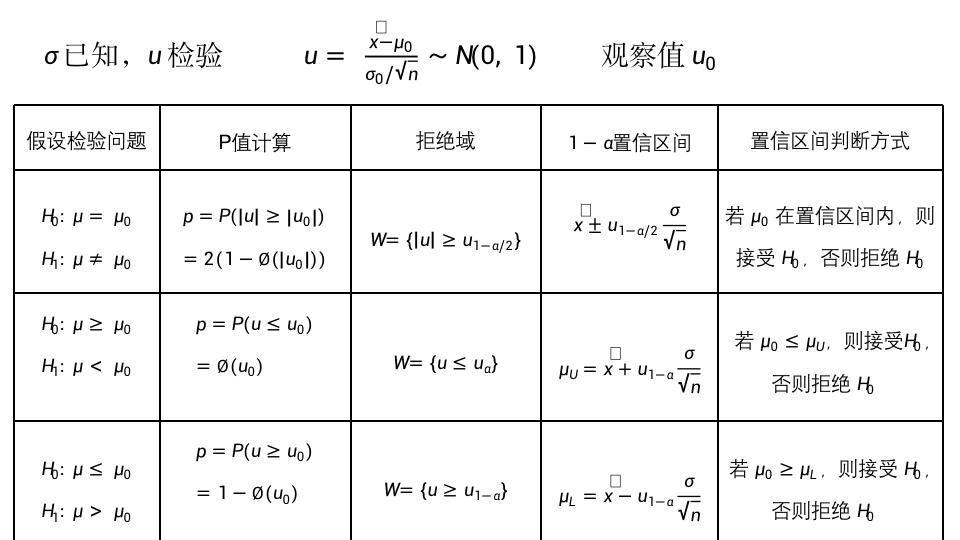
单样本参数假设检验
https://www.cnblogs.com/ywliao/archive/2017/04/17/6724334.html
https://blog.csdn.net/weixin_41261833/article/details/104623377
https://blog.csdn.net/u012429555/article/details/78071728
知道样本的分布,假设总体分布的参数(正态分布的均值,二项分布的概率)是否等于一个常数值
以正态分布来对待,给定显著水平,求p值或者求置信区间(即分位数)
往年出错:分不清
z检验
样本平均数的分布:中心极限定理
中心极限定律:对于任意平均数,标准差为
的总体,样本大小为n的样本平均数分布具有平均数
,标准差
,并且当n趋于无穷时,分布将趋于正态。
1.描述任意总体的样本平均数分布,无论什么样形状、平均数或标准差
求置信区间step by step
qnorm(p) 求z分数
例题:大量检测已知正常人血浆载脂蛋白E总体平均水平为4.15mmol/L,总体分布近似于正态分布。某医师经抽样测得16例陈旧性心机梗死患者的血浆载脂蛋白E平均浓度为4.98mmol/L,标准差为2.78mmol/L。据此能否认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人的平均浓度不一致?并给出置信区间(显著性水平为0.05)
- 建立检验假设H0: μ=μ0,H1: μ不等于μ0,α=0.05,双侧检验
- 计算统计量t
t = (4.98-4.15)/(2.78/sqrt(16))= 1.194245
=qt(1-0.05/2,df=15); =2.13;
-2.13
按α=0.05水准,不拒绝H0,可认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人无显著差别有统计学意义,
置信区间:
m=4.98; s=2.78; n=16
left<‐m‐qt(0.975,n‐1)*s/sqrt(n)
right<‐m+qt(0.975,n‐1)*s/sqrt(n)
left;right
#[1] 3.498643
#[1] 6.461357
95%置信区间为[ 3.498643, 6.461357 ]
t检验
求置信区间step by step
qt(p, df) 求t分数
pt(q,df) 由t分数求概率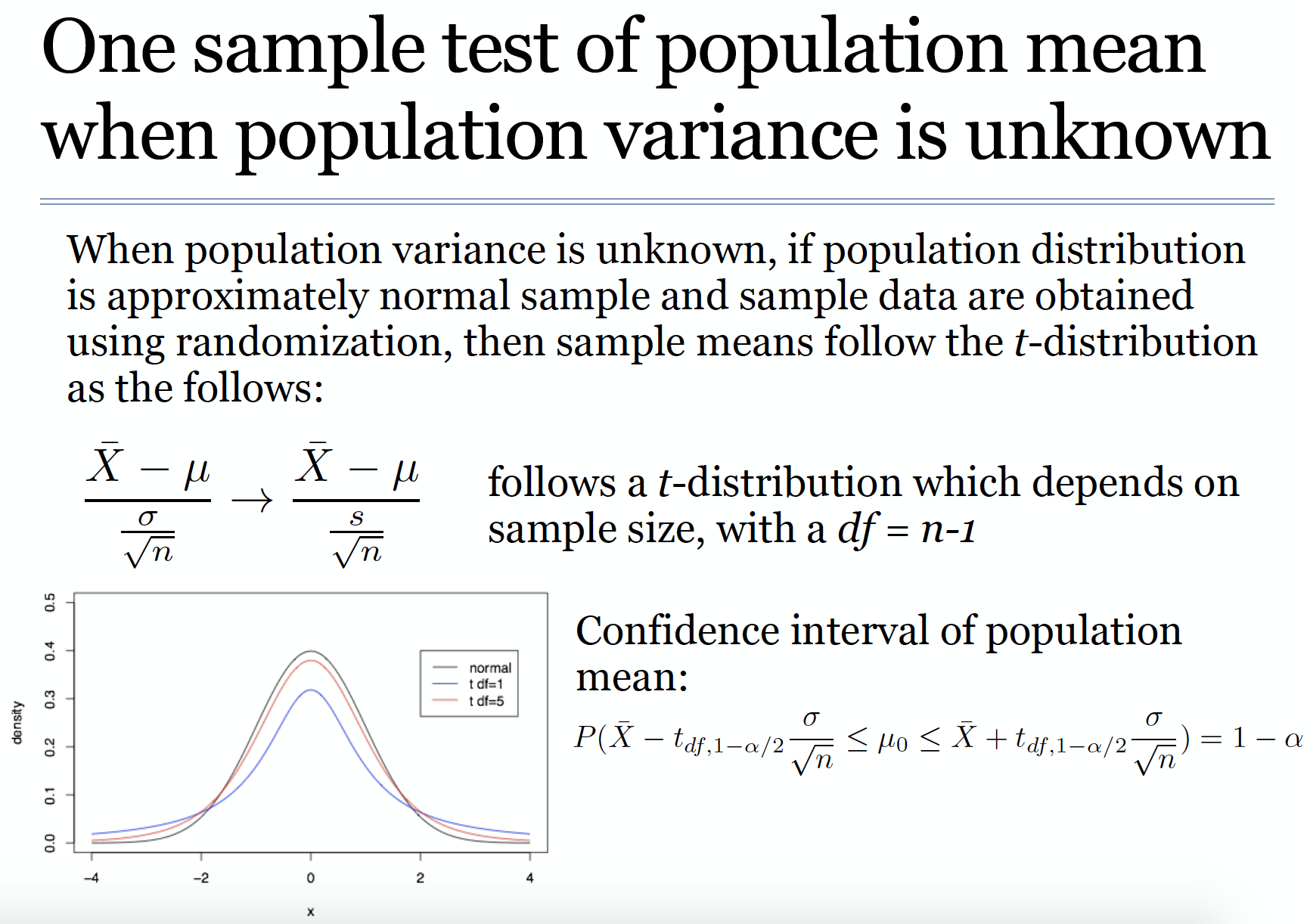
*这里的是s,r中sd()自由度是n-1
例题1:求置信区间
例题2:求置信区间
单边检验双边检验tail
t.test(data, mu=, alternative=,conf.level=0.95默认)
如果是求置信区间,当置信水平为95%时,双边检验是,单边检验是
如果n<30,勉强可以做双边检验,但是单边检验的效果会非常差
关于pt和p值
pt(q, df, ncp, lower.tail = TRUE, log.p = FALSE)默认lower.tail = TRUE的时候,求的是p(tn-1《t),即下图白色区域(接受区域),而p值求的是灰色区域(拒绝区域),所以有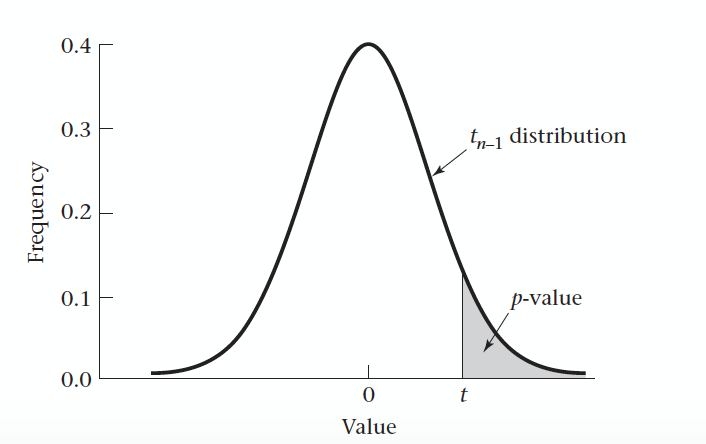
对于右边检验 p=1-pt
对于左边检验 p=pt
对于双边检验 t《0时,p=2pt
t>0时,p=2(1-pt)
例题: 利用上一题的鸢尾花数据集进行计算。鸢尾花的平均花瓣长度为3.5cm,这种说法正确吗?鸢尾花的平均花瓣长度不超过3.5cm吗?鸢尾花的平均花瓣长度不小于3.5cm吗?
鸢尾花的平均花瓣长度为3.5cm,这种说法正确吗?
设总体均值为,假设均值为
。
原假设:(说法正确)
备择假设:(说法不正确)
显著性水平
鸢尾花数据呈正态分布,但总体标准差未知,故选择t检验。
> t.test(iris$Petal.Length, mu= 3.5)
One Sample t-test
data: iris$Petal.Length
t = 1.79, df = 149, p-value = 0.07549
alternative hypothesis: true mean is not equal to 3.5
95 percent confidence interval:
3.473185 4.042815
sample estimates:
mean of x
3.758
P-value>0.05,我们没有充分的理由拒绝原假设,则接受原假设,拒绝备择假设,即该说法正确。
鸢尾花的平均花瓣长度不超过3.5cm吗?鸢尾花的平均花瓣长度不小于3.5cm吗?
对于鸢尾花的平均花瓣长度不超过3.5cm,做右边假设检验
原假设:
备择假设:
> t.test(iris$Petal.Length, mu= 3.5, alternative = 'greater')
One Sample t-test
data: iris$Petal.Length
t = 1.79, df = 149, p-value = 0.03774
alternative hypothesis: true mean is greater than 3.5
95 percent confidence interval:
3.519434 Inf
sample estimates:
mean of x
3.758
P-value<0.05,我们拒绝原假设,接受备择假设,鸢尾花的平均花瓣长度超过3.5cm。
对于鸢尾花的平均花瓣长度不小于3.5cm,做左边假设检验
原假设:
备择假设:
> t.test(iris$Petal.Length, mu= 3.5, alternative = 'less')
One Sample t-test
data: iris$Petal.Length
t = 1.79, df = 149, p-value = 0.9623
alternative hypothesis: true mean is less than 3.5
95 percent confidence interval:
-Inf 3.996566
sample estimates:
mean of x
3.758
P-value>0.05,我们没有充分的理由拒绝原假设,则接受原假设,鸢尾花的平均花瓣长度不小于3.5cm。
卡方分布检验(方差
正态分布的方差服从卡方分布
qchisq(p,df)
pchisq(q,df)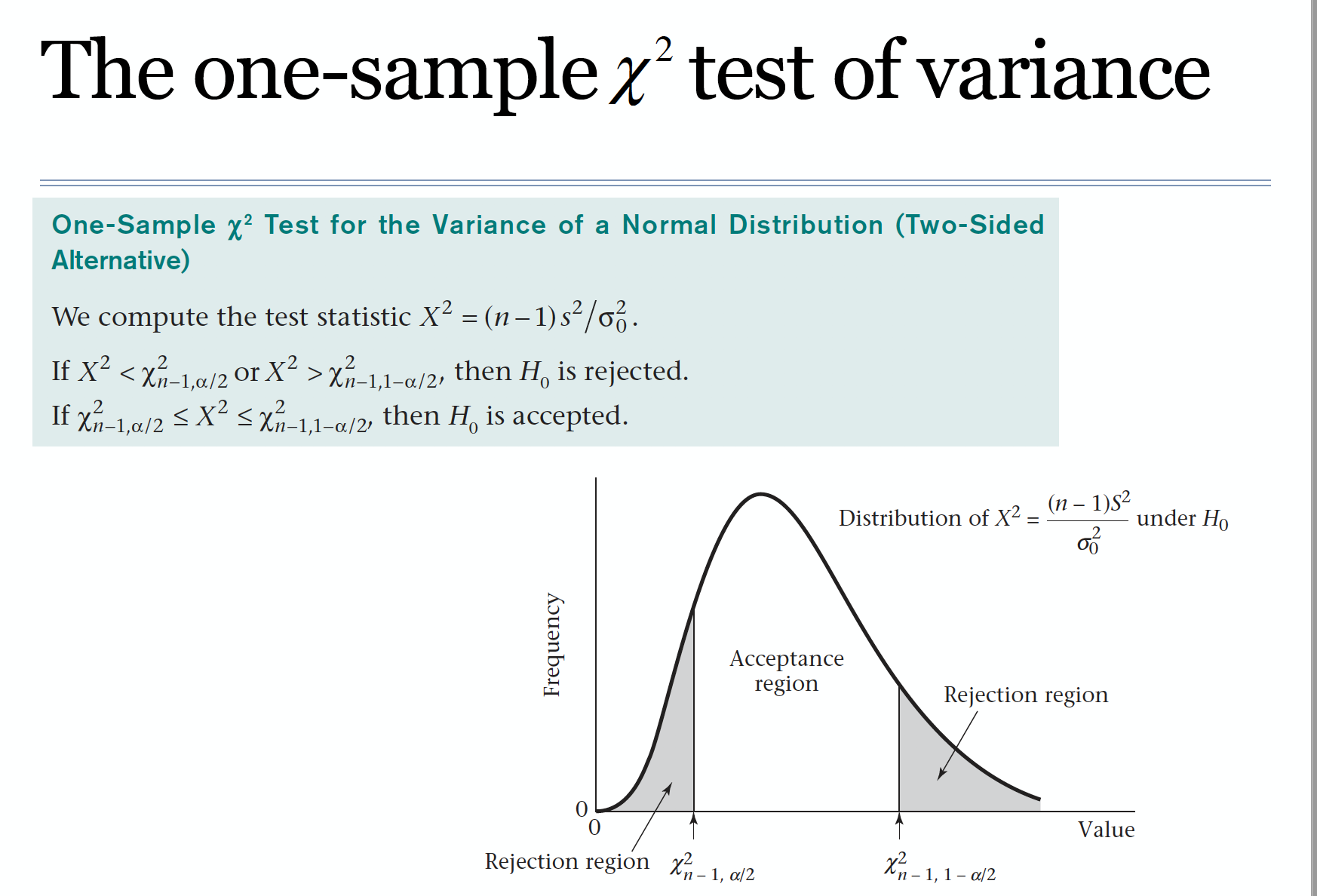
二项分布检验
在样本量足够大时,近似为正态分布
binom.test(x,n,p,alternative=,conf.level=)
例题1:药物是否有效?
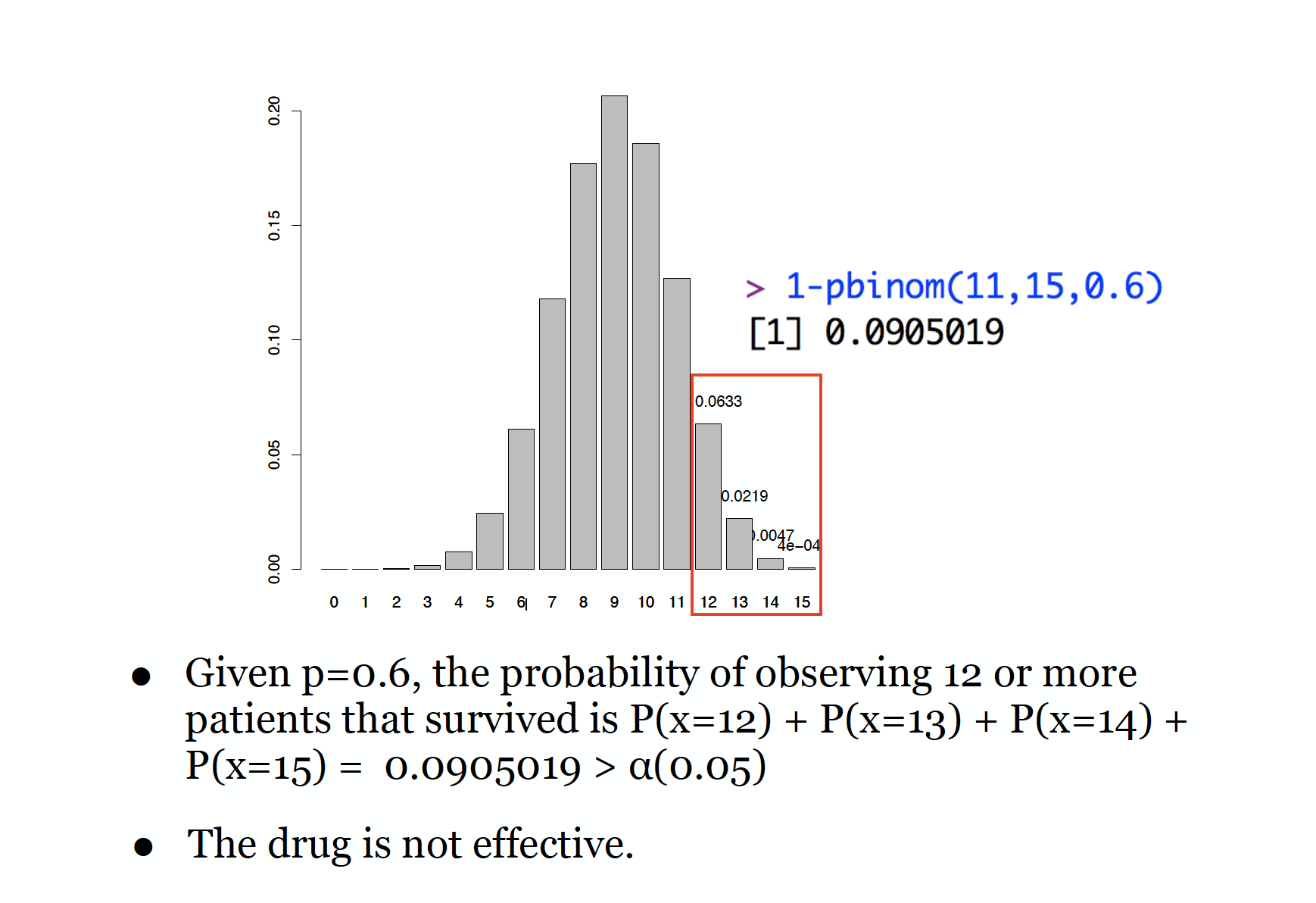
例题2: 据估计,初次购买健身卡月套餐的消费者中,约50%的消费者不会在半年内再次购买健身卡各类套餐。统计人员选取了1月份500个初次购买月卡的消费者,其中210个消费者没有在半年内再次购买健身卡各类套餐(也没有去其他健身房办理健身卡)。问:在0.001显著性水平上,是否有证据表明这类消费者(指初次购买后,半年内没有再次购买健身卡各类套餐的消费者)比例低于50%?
假设x是样本中不买的次数,n是样本总数,p=0.5,,做二项分布参数检验。
> binom.test(210,500,p=0.5,alternative = 'less',conf.level = 0.999)
Exact binomial test
data: 210 and 500
number of successes = 210, number of trials = 500, p-value = 0.0002002
alternative hypothesis: true probability of success is less than 0.5
99.9 percent confidence interval:
0.0000000 0.4899294
sample estimates:
probability of success
0.42
P-value<0.05,我们拒绝原假设,接受备择假设,在0.001显著性水平上,这类消费者(指初次购买后,半年内没有再次购买健身卡各类套餐的消费者)比例低于50%。
统计功效及样本容量
四个量(样本大小、显著性水平、功效和效应值)紧密相关,给定其中任意三个量,便可推算第四个量。下三图示意了四者的相互影响。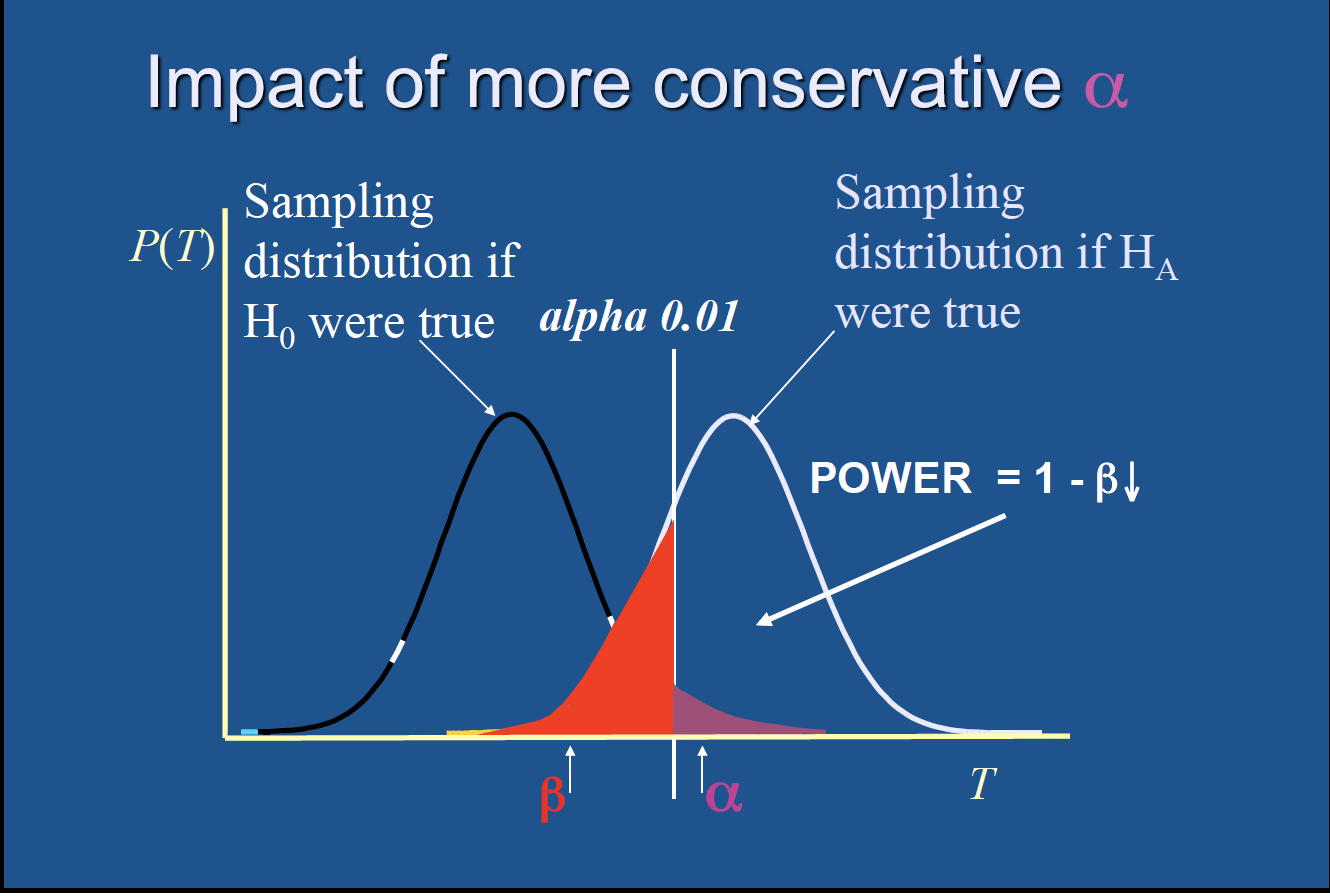
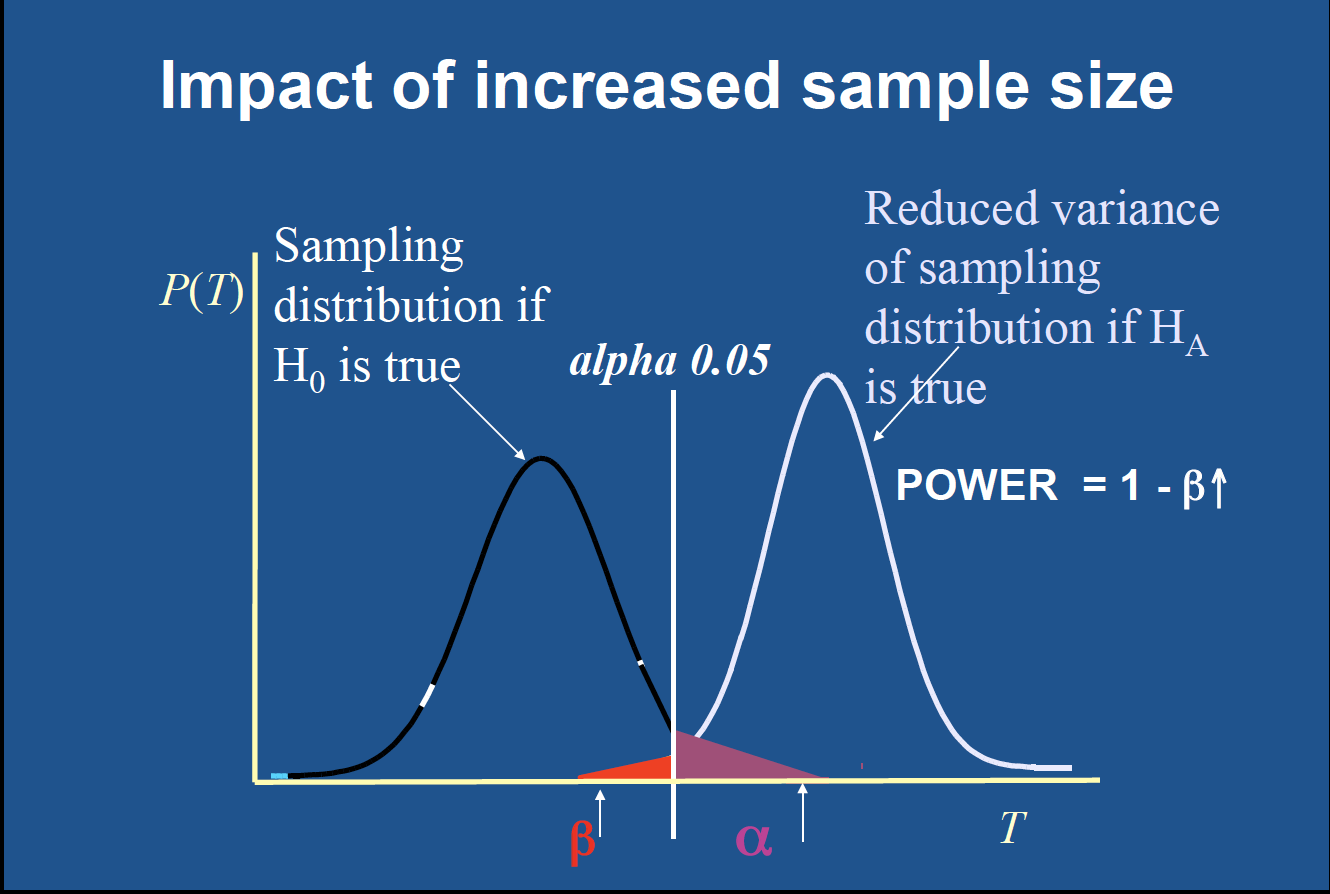
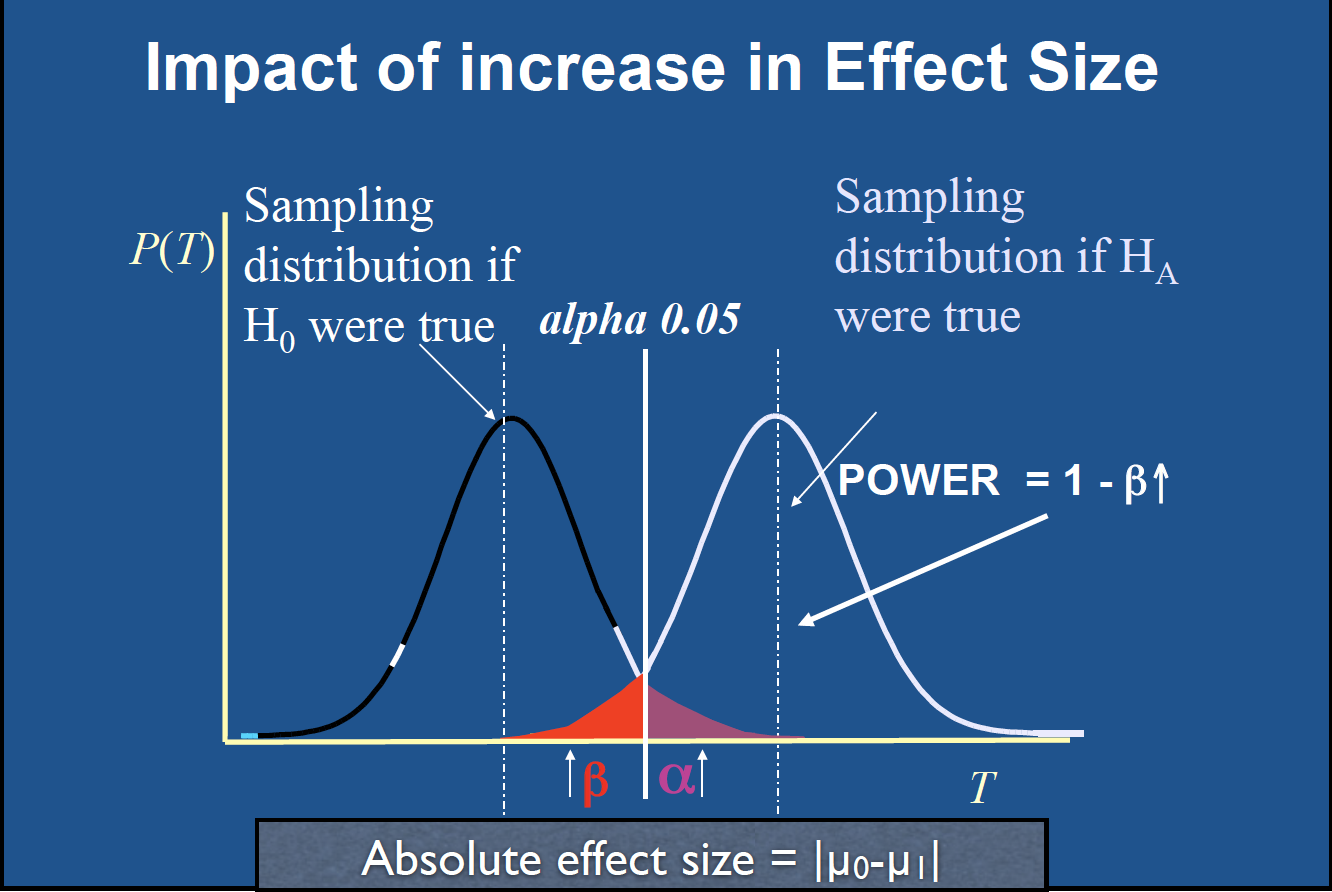
统计功效
公式
f分布求分位值
power<-pt(qt(0.05,9)+(mean(BMI2)-23.2)/sd(BMI2)*sqrt(10),9)

muA=5
muB=10
kappa=1 # 即k值
sd=10
alpha=0.05
nB=63
z=(muA-muB)/(sd*sqrt((1+1/kappa)/nB))
Power=pnorm(z-qnorm(1-alpha/2))+pnorm(-z-qnorm(1-alpha/2))
样本容量
公式
(qnorm(1‐0.05)+qnorm(1‐0.001))^2* sd(BMI2)^2/(mean(BMI2)‐23.2)^2
pwr包
效应值
library(pwr)
delta<-(mean(BMI2)-23.2)/sd(BMI2)
power<-pwr.t.test(n=10,d=delta,sig.level = 0.05,type = "one.sample",alternative = "greater")$power
power
pwr.t.test(d=delta,sig.level = 0.001,power=0.95,type = "one.sample",alternative = "greater")$n
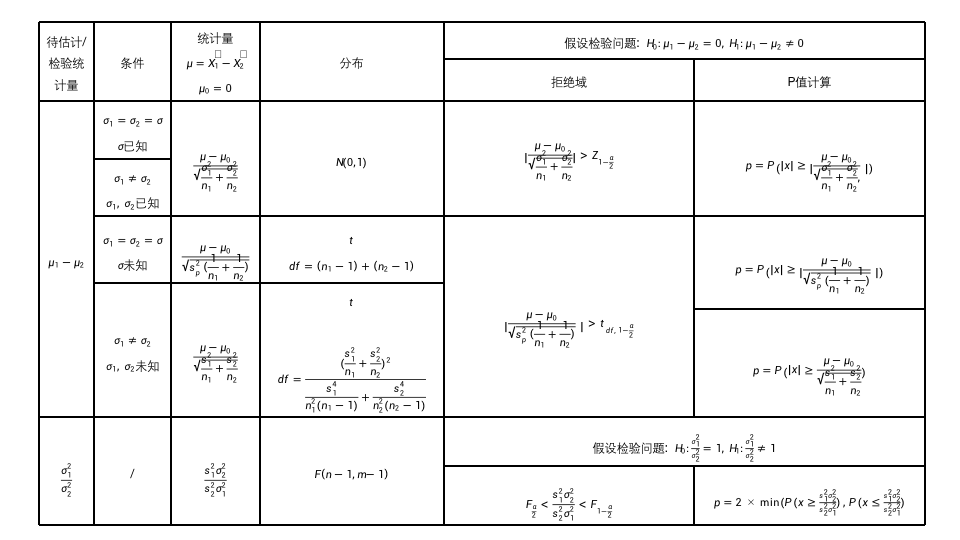
双样本参数假设检验
方差齐性检验
F检验
var.test(a,b)
F test to compare two variances
bartlett检验
bartlett.test(value~cls,folic_acid)
配对检验
配对t检验
正态性,方差齐性
t.test(data1,data2,paired=TRUE)
多次假设检验p值校正
bonferroni校正
fdr校正
将p值升序排列
设置FDR水平,选择到排序到满足下列条件的j
#bonferroni校正
bonferroni_adj_pvalue = p.adjust(pvalue_vector, method="bonferroni")
sum(bonferroni_adj_pvalue < 0.01)
[1] 364
#fdr校正
fdr_adj_pvalue = p.adjust(pvalue_vector, method="fdr")
sum(fdr_adj_pvalue < 0.01)
[1] 1049
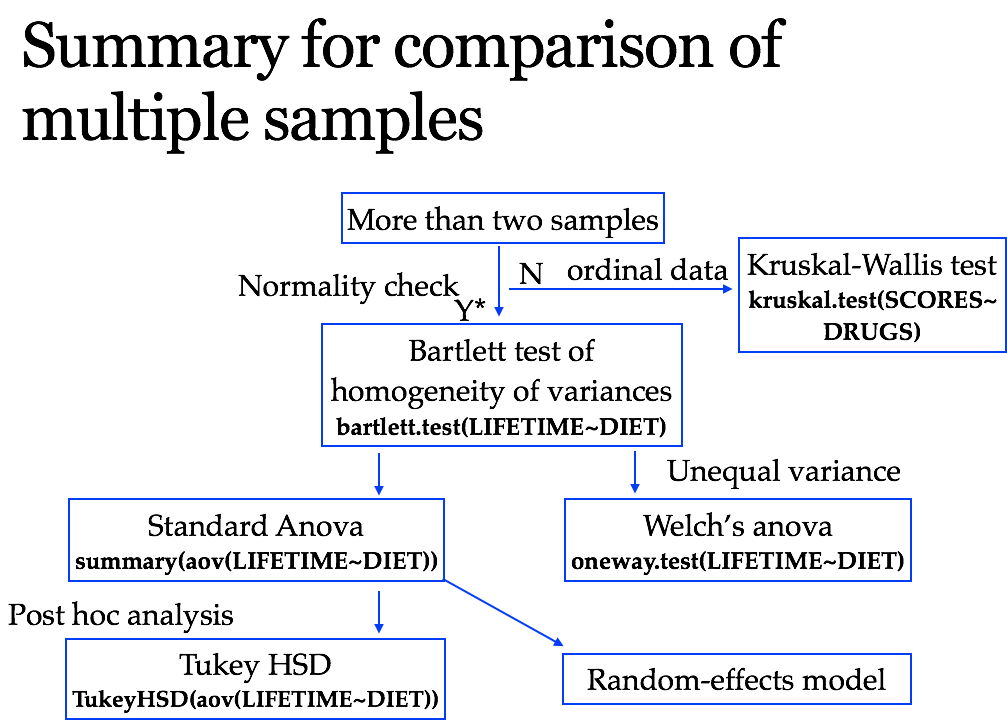
非参数假设检验
wilcon rank sum test
wilcox.test(a,b,paired = F, alternative = “two.sided”,exact = F)
kruskal-wallis test
kruskal.test(value ~ variable, data_conv)
方差分析
aov(output~factor,data=)其实是f检验
anova分析step by step
例题:1, 22 bypass-patients are randomly divided into 3 treatment groups (different respiration). Differ the values of folic acid in red blood cells after 24 h? Hint: step-by-step anova, α = 0.05(25分__)
Group1: 243, 251, 275, 291, 347, 354, 380, 392
Group2: 206, 210, 226, 249, 255, 273, 285, 295, 309
Group3: 241, 258, 270, 293, 328
先把数据导入成一列是value,一列是factor的形式/rep()或reshape2包
reshape2::melt数据融合
rep(fator名,length(group))如下
Step1: import data
> group1<-c(243, 251, 275, 291, 347, 354, 380, 392)
> group2<-c(206, 210, 226, 249, 255, 273, 285, 295, 309)
> group3<-c(241, 258, 270, 293, 328)
> folic_acid <-data.frame(value=c(group1,group2,group3),cls=c(rep("G1",length(group1)),rep("G2",length(group2)),rep("G3",length(group3))))
Step2: check normality & variance equality
> shapiro.test(group1)
Shapiro-Wilk normality test
data: group1
W = 0.90704, p-value = 0.3337
> shapiro.test(group2)
Shapiro-Wilk normality test
data: group2
W = 0.9469, p-value = 0.6561
> shapiro.test(group3)
Shapiro-Wilk normality test
data: group3
W = 0.96355, p-value = 0.8325
> bartlett.test(value~cls,folic_acid)
Bartlett test of homogeneity of variances
data: value by cls
Bartlett's K-squared = 2.0951, df = 2, p-value = 0.3508
Step3: F test compare means of 3 groups
> total_mean <- mean(folic_acid$value)
> S_means <- aggregate(folic_acid$value,by=list(group=folic_acid$cls),mean)
S_vars <- aggregate(folic_acid$value,by=list(group=folic_acid$cls),var)
S_lens <- aggregate(folic_acid$value,by=list(group=folic_acid$cls),length)
> S_vars <- aggregate(folic_acid$value,by=list(group=folic_acid$cls),var)
> within_SS <- sum((S_lens$x-1) * S_vars$x)
> total_SS <- sum((folic_acid$value - total_mean)^2)
> between_SS <- total_SS - within_SS
> df_between <- 3 - 1
> df_within <- nrow(folic_acid) - 3
>
> between_MS <- between_SS/df_between
> within_MS <- within_SS/df_within
>
> F_statistic <- between_MS/within_MS
> p_value <- 1 - pf(F_statistic, df_between, df_within)
> p_value
[1] 0.04358933
P<0.05, reject H0, significant difference exists in three groups.
one way/ two way
two way:summary(aov(len~suppdose,data=data4)) 因子剂量
事后检验
pairwise t test
pairwise.t.test(dat$yield,dat$seed,p.adjust.method = “none”)
Tukey HSD test
TukeyHSD(aov(yield~seed,data=data3))
独立性检验
线性回归
一元线性模型
myfit = lm(formula即y~x, data)
abline(myfit) 在散点图上画出拟合直线(需要先画出散点图)
summary(myfit) 看统计内容
residuals(myfit) 残差
多元线性模型
ff = lm(y~x1+x2)
summary(ff)
cor(data) 算相关系数
predit()预测值
exa <- data.frame(x1 = 200, x2 = 3000)
lm.pred <- predict(lm.reg, exa, interval = "prediction", level = 0.95)
R方step by step
Calculate R^2 , test the hypothesis H_0: β_1=β_2=0 vs.H_1: either β_1≠0 or β_2≠0 (step by step)
>>>
#(1)Estimate the regression parameters using the method of least squares, and compute Reg SS and Res SS
TotalSS <- sum((dat3$crop_yield-mean(dat3$crop_yield))^2)#13.45859
predicts=predict(crop_yield_lm,newdata = dat3,level = 0.95,interval = "prediction")
ResSS= sum((dat3$crop_yield-predicts[,1])**2)
#1.431813
RegSS <- TotalSS – ResSS
#12.02677
R2 <- RegSS/TotalSS
#0.8936135
#(2) Compute Reg MS Reg SS/k, Res MS Res SS/(n − k − 1).
RegMS <- RegSS/3
#4.008925
ResMS <- ResSS/(length(dat3$crop_yield)-3-1)
#0.05506972
#(3) Compute the test statistic which follows an F(k,n−k−1) distribution under H0
Fstat <- RegMS/ResMS # 72.79727
#(4) F test and calculate Pvalue
pf(Fstat,df1 = 3,df2 =length(dat3$crop_yield)-3-1,lower.tail = FALSE)
#8.883415e-13
#(5)reject H0,accept H1
逻辑回归模型
比较回归模型是否有显著差异 用anova
对于两个线性回归模型:anova(f, f_reduced)
对于两个逻辑回归模型:anova(f, f_reduced, test = ‘Chisq’)
计算accuracy
testingset$yp = predict(fit2.reduced,newdata = testingset,type='response')
ntrue = length(intersect(which(testingset$yp>=0.5),which(testingset$yndefault==1)))
nfalse = length(intersect(which(testingset$yp<0.5),which(testingset$yndefault==0)))
accuracy = (ntrue+nfalse)/length(testingset$yp)
accuracy
条件回归
PCA
https://www.cnblogs.com/leezx/p/6120302.html
prcomp(data,center=T,scale=T)scale为标准化
princomp(data,默认cor=F)默认使用协方差矩阵做特征值分解,cor=T使用相关性矩阵做特征值分解(即对raw data做了z score 标准化)
聚类分析
hclust函数
例题:(1)调用R内置数据iris,根据花萼及花瓣的长度和宽度进行聚类分析 (hclust函数),并画出聚类结果图。
(2)根据聚类的结果将数据分为三类,并列表说明聚类的结果与原始数据的分类的区别。
1.
> data(iris)
> iris.hc <- hclust(dist(iris[,1:4]))
> plot(iris.hc, hang = -1)
2.
> re <- rect.hclust(iris.hc, k=3)
> iris.id <- cutree(iris.hc, 3) #标注出3个类
> table(iris.id, Species)
Species
iris.id setosa versicolor virginica
1 50 0 0
2 0 23 49
3 0 27 1
从聚类结果看,明显与原始数据有着比较大的差异。
基因差异表达+富集分析
fold change+热图+fisher exact test
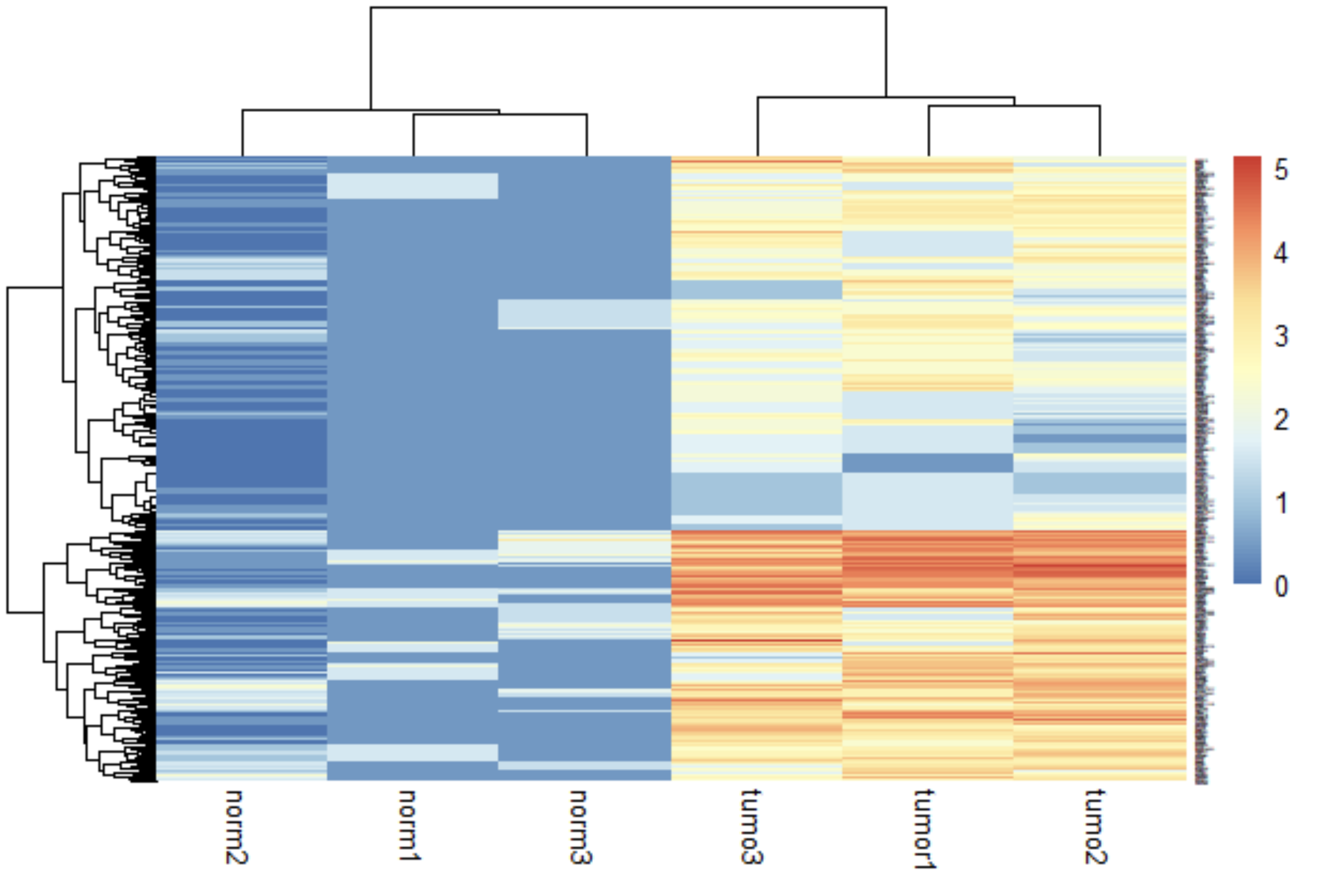
例题第二问:3. To study genes that are highly expressed in breast cancer, one student in sibcb took three tumor samples and three healthy samples then performed RNA sequencing, homework7_data3.txt is the gene expression matrix.
(1) Now, load the data into R, then draw density plots and box plot for the samples. Find the gene with the highest expression level in norm tissue and in tumor tissue. Then perform normalization (using the function ”normalizeQuantiles” in package limma) and perform log transform: ‘log2(data+1)’ for the data, draw a boxplot plot after both normalization and log transform.
(2) Using the transformed data, try to find how many genes are highly expressed in breast cancer. (foldchange > 1.5 and pvalue < 0.05 ).
(3) Using highly expressed genes to draw a heatmap for normal and tumor samples(using function pheatmap in package pheatmap)
(4) The student was interested in kegg pathway “Glycolysis_gluconeogenesis”, he wanted to known whether the highly expressed genes were enriched in the pathway, try to do the enrichment using fisher exact test. Known genes annotated with this pathway are listed in “homework7_kegg.txt”.
(1)
data3 = read.table("homework7_data3.txt", sep="\t")
plot(density(data3$norm1), main="norm1")
…
plot(density(data3$tumor3), main="tumor3")
boxplot(data3, main = "boxplot"
data3$sumnorm <- apply(data3[,1:3],1,sum)
data3$sumtumor <- apply(data3[,4:6],1,sum)
row.names(data3)[order(data3$sumnorm,decreasing = T)[1]]
# "7223"
row.names(data3)[order(data3$sumtumor,decreasing = T)[1]]
# "652991"
#normalization
install.packages("limma")
library("limma")
data3_norm = normalizeQuantiles(data3[,1:6])
boxplot(data3_norm, main = "boxplot_norm")
data3_norm_log = log2(data3_norm+1)
boxplot(data3_norm_log, main = "boxplot_norm_log")
(2)
data3_norm_log$pvalue = apply(data3_norm_log, 1, function(x){if(var.test(as.numeric(x[1:3]), as.numeric(x[4:6]))$p.value > 0.05) t.test(as.numeric(x[1:3]), as.numeric(x[4:6]), alternative = "less", var.equal = T)$p.value else t.test(as.numeric(x[1:3]), as.numeric(x[4:6]), alternative = "less", var.equal = F)$p.value})
data3_norm_log$foldchange = apply(data3_norm_log[,1:6],1,function(x) (mean(x[4:6])-mean(x[1:3]))/min(mean(x[4:6]),mean(x[1:3]))) 或者直接是mean(x[,4:6])/mean(x[,1:3])就可以
up_genes = row.names(data3_norm_log)[which(data3_norm_log$pvalue< 0.05 & data3_norm_log$foldchange>1.5)]
length(up_genes)
#487
(3) install.package(“pheatmap”)
library(pheatmap)
up_gene_matrix = data3_norm_log[which(data3_norm_log$pvalue< 0.05 & data3_norm_log$foldchange>1.5),1:6]
pheatmap(up_gene_matrix)
(4)
(4) kegg_list = read.table("homework7_kegg.txt")
up_in_list = length(intersect(up_genes, kegg_list))
up_out_list = length(up_genes) - up_in_list
all_except_up_in_list = length(intersect(row.names(data3), kegg_list)) - up_in_list
all_except_up_out_list = dim(data3)[1] - up_in_list - up_out_list - all_except_up_in_list
rnames<-c("In anno group","Not in anno group")
cnames <- c("Gene list","Genome")
counts <- matrix(c(up_in_list, up_out_list, all_except_up_in_list, all_except_up_out_list),nrow = 2,dimnames = list(rnames,cnames))
counts
# Gene list Genome
#In anno group 2 11
#Not in anno group 485 5864
P1: Proportion of UP genes in KEGG list; P2: Proportion of kegg list in Genome
null hypothesis and alternative hypothesis:
#H0:P1 = P2 #H1:P1 > P2
fisher.test(counts,alternative = "greater")
# Fisher's Exact Test for Count Data
#
# data: counts
# p-value = 0.2621
# alternative hypothesis: true odds ratio is greater than 1
# 95 percent confidence interval:
# 0.3480003 Inf
# sample estimates:
# odds ratio
# 2.197869
p-value > 0.05, don’t reject H0, up expressed genes are not enriched in kegg pathway “Glycolysis_gluconeogenesis”.
包packages
基本操作
下载包install.packages(‘package’)
多个包install.packages(c("package 1","package 2",···))
指定路径install.packages("E:/vegan.rar") #需要绝对路径
更新包update.packages()
显示库所在的位置.libPaths(), 函数library()则可以显示库中有哪些包。计算机上存储包的目录称为库(library)
加载包library(package)或require(package name) 。
查看默认加载包getOption(“defaultPackages”)
查看已加载的R包(.packages())/search()
查看所有已安装的R包(.packages(all.available = T))或installed.packages()
卸载包remove.packages(“package name”,.Library)
列出该包可用的函数和数据集help(package=’package’)
工具链tidyverse
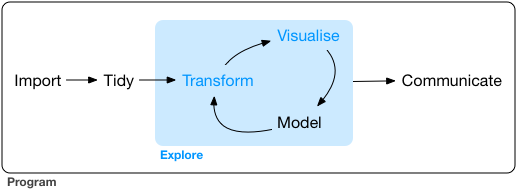
加载包library(tidyverse)
ggplot
使用+号
快速实现拆分画图
facet_wrap(~class)
ggplot(data=mpg数据必须是数据框)+geom_point几何对象(mapping=aes(x=displ, y=hwy,color=class将数据映射到图形中))+facet_wrap(~class)第3个维度的信息可以像前面一样用不同的颜色显示也可以分开来画图
散点图拟合
上面的另外一种写法ggplot(mpg, aes(x=displ, y=hwy))+geom_point()+geom_smooth(method=’lm’)
默认方法是losess近邻多项式回归(非参数方法),阴影部分是置信区间的上下界
lm是线性回归
->参考快捷手册ggplot2-cheatsheet
直方图
# Code01-01(P.25 01-06)
# ======================
# R语言会忽略井号(#)右侧的命令。我们可以利用这一性质,将笔记或注释写在#右侧
choujiang <- c("未中奖","一等奖")
# 现在是要每天抽100次奖,重复7天,然后统计一等奖出现的次数
# 我们写一条命令让上述过程重复执行1000次,并将结果以res为名称保存
# 格式:replicate(1000, sum(replicate(7, 抽100次奖时出现一等奖的次数)))
res <- replicate(1000, sum(replicate (7, sample (choujiang, 100, prob = c(99,1), replace = TRUE) ) == "一等奖"))
# 简单的直方图
hist(res, breaks = 0:18)
# 如果想生成更精致的图,需要安装制图软件包ggplot2(需要网络)
install.packages("ggplot2")
library(ggplot2) # 使用前需要先加载
# 对抽奖数据稍作加工,以便用ggplot2程序包绘图
resD <- as.data.frame(table(res))
# 只显示头10行数据
head(resD, n = 10)
# 实际绘图
ggplot(resD, aes(y = Freq, x = res)) + geom_histogram(binwidth = 1, stat="identity", fill = "steelblue") + xlab("该周大奖出现次数") + ylab ("周数") + ggtitle("直方图") + theme(text = element_text(family = "Heiti SC Light"))
# 若图中的汉字无法正常显示,可通过“ + theme(text = element_text(family = "Heiti SC Light"))”指定汉字的字体
# 在最新版本的ggplot2程序包中,由于geom_histogram函数的格式发生了变化,
# 所以若上面的最后1行代码执行后报错(Error: Unknown parameters: binwidth, bins, pad),请改用下面这2行代码生成直方图
resD <- as.data.frame(res)
ggplot(resD, aes(x = res)) + geom_histogram(binwidth = 1, color = "white", fill = "steelblue") + xlab("该周大奖出现次数") + ylab ("周数") + ggtitle("直方图") + theme(text = element_text(family = "Heiti SC Light"))
条形图
table1 <- survey %>% select (立场, 回答6) %>% table
table1 %>% as.data.frame %>% ggplot(aes (x = 立场, y = Freq, fill = 回答6 )) + geom_bar(stat="identity") + ylab("人数") + theme(text = element_text(family = "Heiti SC Light")) #+ scale_fill_grey(start = 0.4, end = 0.8)
时间序列图
scale_x_date()
fantuan %>%ggplot(aes(日期, 销售额)) + geom_line() + scale_x_date() + ggtitle("饭团的销售额") + theme(text = element_text(family = "Heiti SC Light"))
散点图矩阵
# Code04-04(P.131 04-03)
# ========================
# 相关系数
# 导入用于数据整形的程序包
install.packages("tidyr")
library(tidyr)
# 将用来生成相关矩阵的品名列为横轴
noodles2 <- menus %>% filter (品名 %in% c("饭团", "味噌汤", "咖喱", "茶泡饭", "意大利面", "酱汁炒面", "乌冬面", "什锦面", "拉面")) %>% select (品名, 销售额, 日期) %>% spread(品名, 销售额)
# 查看开头
noodles2 %>% head # head(noodles2)
# 求相关系数(指定-1来忽略日期部分)
noodles2[, -1] %>% cor # cor(noodles2[, -1])
# 也可以写成
noodles2 %>% select (-日期) %>% cor
# 散点图矩阵
noodles2[, -1] %>% pairs #pairs(noodles2[, -1])
dplyr
可以用管道操作简化嵌套操作%>%表示操作向右流动(来自magrittr包)
func_3(func_2(func_1(data, arg1 = haha),arg2 = huhu), arg3 = hoho)
data %>% func_1(arg1 = haha) %>% func_2(arg2 = huhu) %>% func_3(arg3 = hoho)
筛选行filtter()
mpg %>% filter(displ >=5 , hwy < 20)
排序arrange()
mpg %>% filter(displ >=5 , hwy < 20) %>% arrange(desc(year) , hwy)
单独提取变量(相当于筛选列)select()
mpg %>% filter(displ >=5 , hwy < 20) %>% arrange(desc(year) , hwy) %>% select(model)
可以操纵mutate(),算均值方差啥的
mpg %>% mutate(ave_displ= displ / cyl) %>% select(ave_displ)
var(mpg %>% mutate(ave_displ= displ / cyl) %>% select(ave_displ))
分组group_by(),然后用summarise()计算统计学特征
mpg %>% group_by(class) %>% summarise(mean(displ) , mean(hwy))