堆（Heap）
堆排序的关键词：原地、时间复杂度堆 - 图1 、排序算法

什么是堆

堆是一种特殊的树。

堆是完全二叉树：完全二叉树，除了最后一层，其他层的节点个数都是满的，最后一层的节点靠左排列。
堆中每个节点的值都必须大于等于（或小于等于）其子树中每个节点的值：堆中每个节点的值都大于等于（或小于等于）其左右子节点的值。

大顶堆：每个节点的值大于等于左右子节点的值的堆
小顶堆：每个节点的值小于等于左右子节点的值的堆

实现堆

主要问题：如何存储一个堆 和 堆支持哪些操作。

数组存储堆

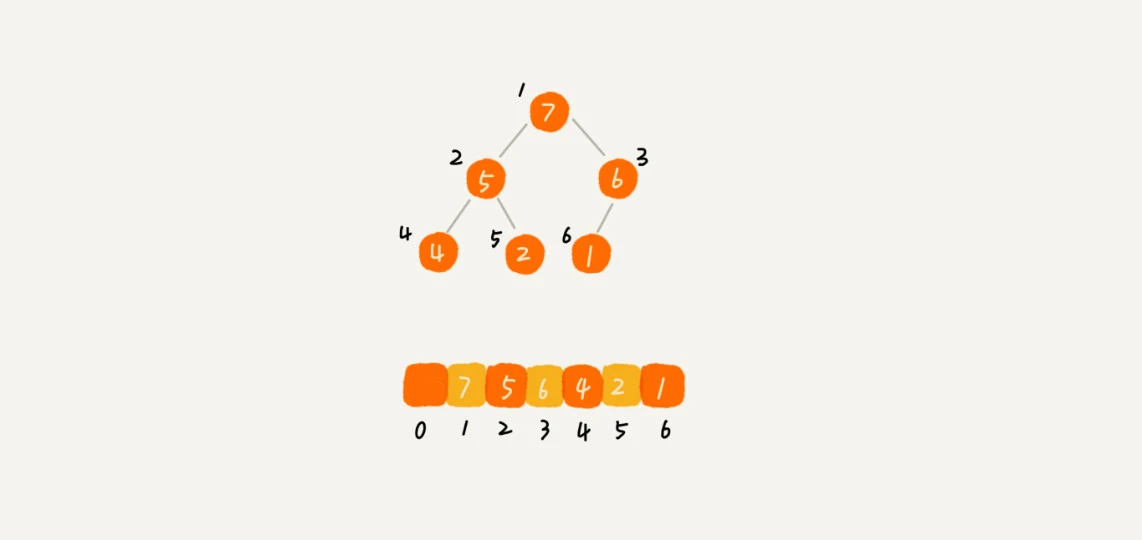
数组下标为 i 的几点的左节点，就是下标为 2 i 的节点，右节点是 2 i + 1 的节点。父节点是 i / 2 的节点。

插入元素

往堆中插入元素后，仍需要保持其满足堆的两个特性。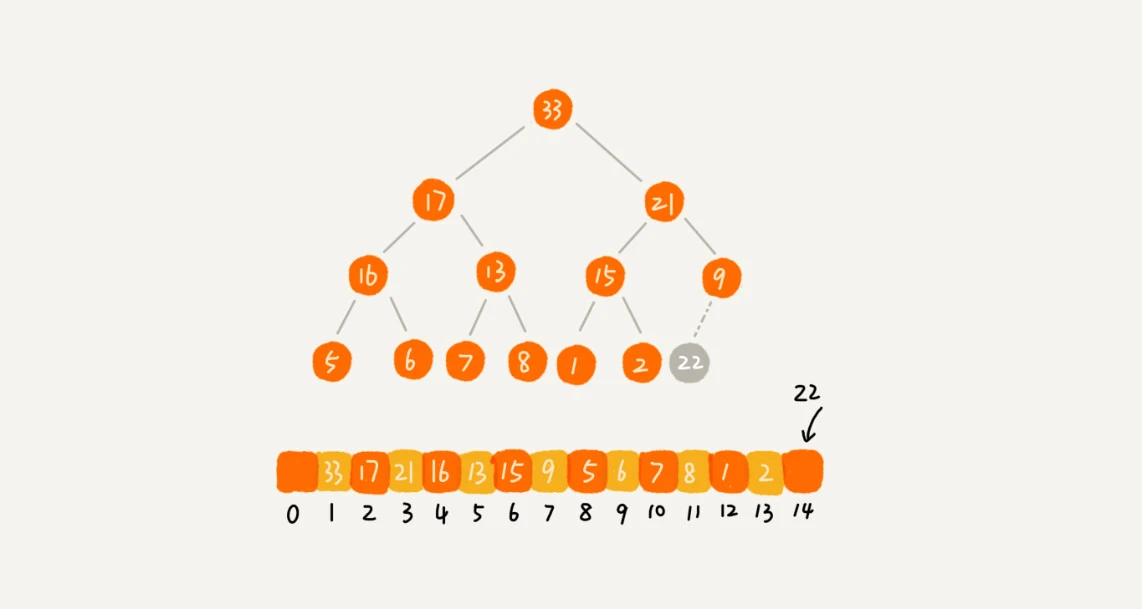

如果把新插入的元素放到堆的最后，我们需要调整这个堆，使其满足堆的特性，这个过程成为是堆化（heapify）
堆化有从下往上和从上往下。

从下往上堆化

顺着节点所在的路径，向上比较，然后交换。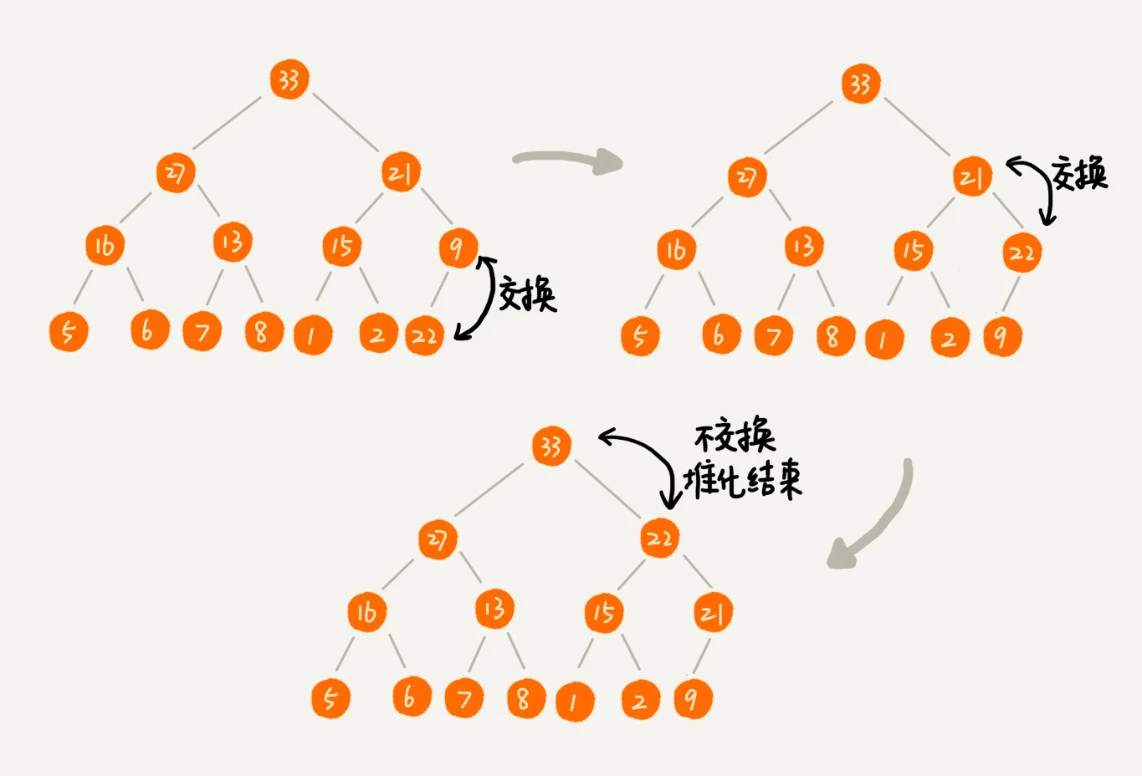

class Heap {
  private a : Array<number> // 数组，从下标 1开始存储数据
  private n : number // 堆可以存储的最大数据个数
  private  count : number // 堆当前已经存储的数据个数
  public contructor(capacity: number) {
    this.a = new Array(capacity + 1)
    this.n = capacity
      this.count = 0
  }
  public insert(data: number) {
    if (this.count > this.n) {
      return
    }
    this.count++
    this.a[this.count] = data
    let i = this.count
    while( i >> 1 > 0 && this.a[i] > a[i >> 1]) {
      [a[i], a[i >> 1]] = [a[i >> 1], a[i]]
      i = i >> 1
    }
  }
}

删除堆顶元素

假设我们构造的是大顶堆，堆顶是最大的元素，那么当我们删除堆顶元素之后，需要把第二大的元素放到堆顶，那么第二大的元素肯定出现在左右子节点中。然后我们就迭代地删除第二大节点即可。
那么按照这个操作可能会导致数组空洞。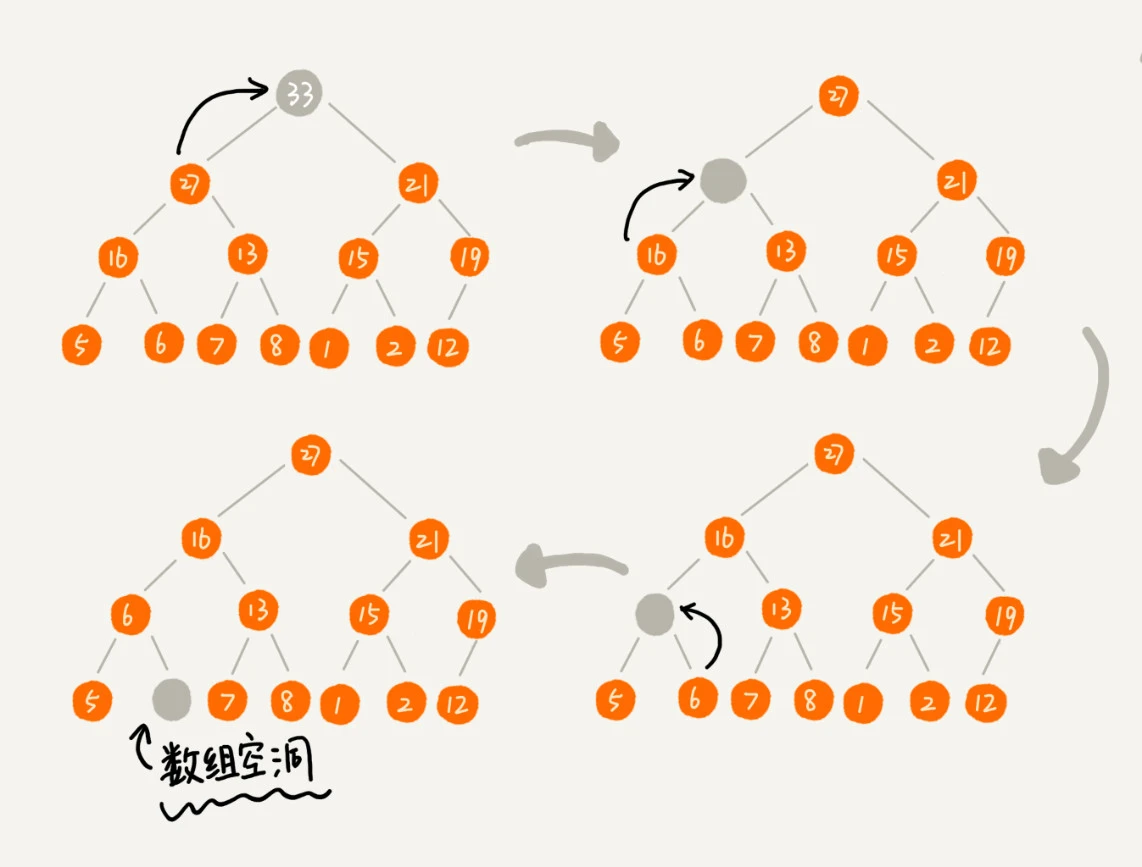

从上往下堆化

升级一下思路，当删除堆顶之后，将最后一个节点放到堆顶，然后利用同样的父子节点对比的方法，对于不满足父子节点大小关系的，互换两个节点，重复这个过程，直到父子节点之间满足大小关系位置，这个过程就是从上往下堆化。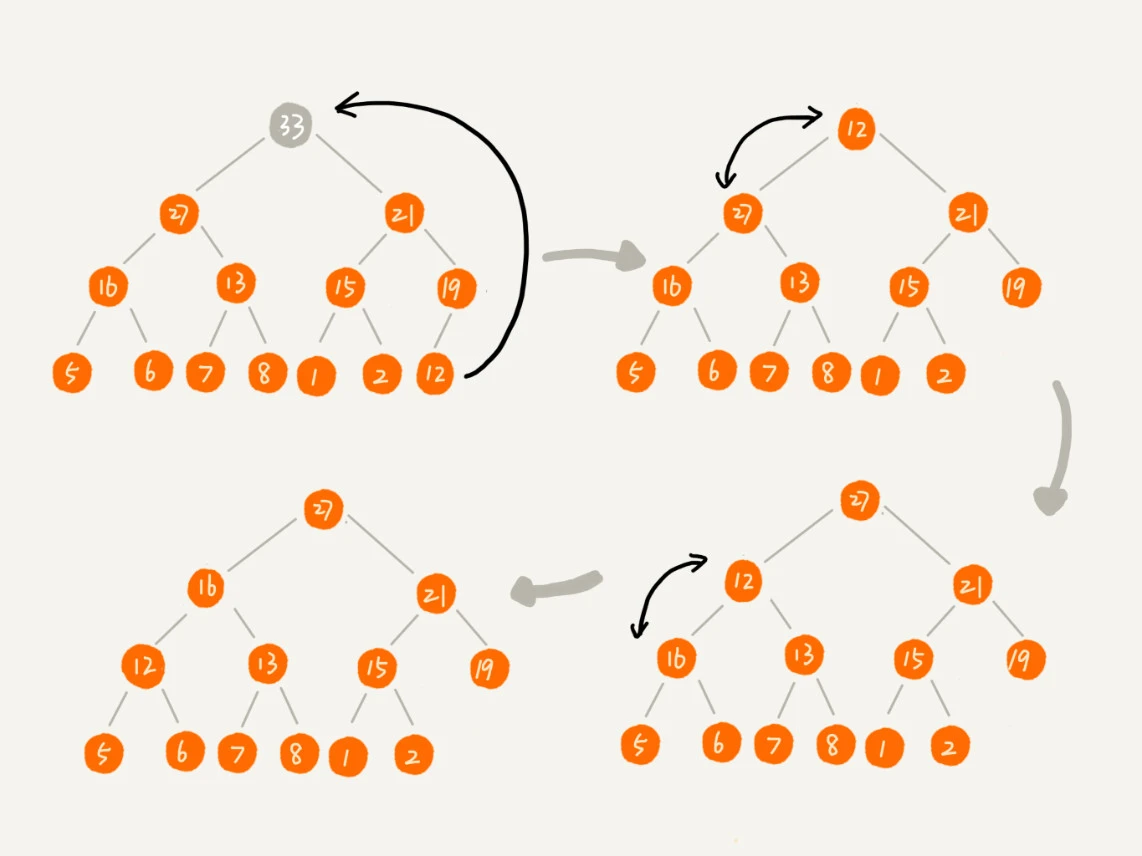

public removeMax(): number {
  if (this.count == 0) return -1
  this.a[1] = this.a[this.count]
  this.count --
  this.heapify(this.a, this.count, 1)
}
private heapify(a: Array<number>, n :number, i:number) {
  while(true) {
    let maxPos = i
    if (i*2 <= n && a[i] <a[i*2]) maxPos = i * 2
    if (i *2 + 1 <= n && a[maxPos] <a[i*2 + 1]) maxPos = i * 2 + 1
    if maxPos == i  break
    [a[i], a[maxPos]] = [a[maxPos], a[i]]
    i = maxPos
  }
}

插入一个元素和删除堆顶元素的事件复杂度都是堆 - 图7 。

实现堆排序

关键词：原地排序算法、堆 - 图8

1. 建堆

数组原地建成一个堆。
思路1：按照堆中插入元素的思路建立。假设起初堆中只有一个数据，就是下标为 1 的数据，然后调用前面的插入操作，将下标为 2 到 n 的数据一次插入堆中即可。从前往后处理数组数据，从下往上堆化
思路2：从后往前处理数组数据，从上往下堆化。

这里主要讲的是思路2 。
这里的关键是，因为叶子节点是往下堆化只能自己跟自己比较，所以我们直接从最后一个非叶子节点开始堆化。
依次是 8、19、5、7

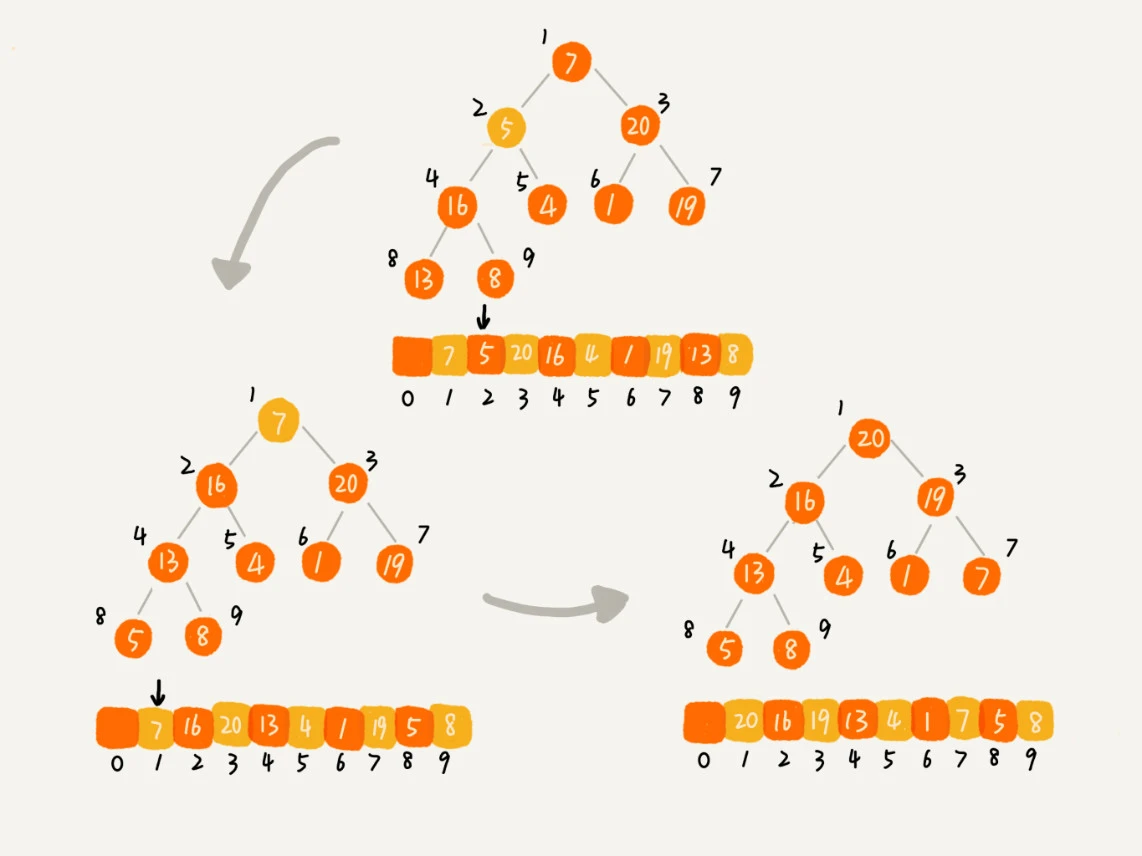
private buildHeap(a: Array<number>, n: number) {
  for (let i = n >> 1; i >= 1; --i) {
    heapify(a, n, i)
  }
}
private heapify(a: Array<number>, n :number, i:number) {
  while(true) {
    let maxPos = i
    if (i*2 <= n && a[i] <a[i*2]) maxPos = i * 2
    if (i *2 + 1 <= n && a[maxPos] <a[i*2 + 1]) maxPos = i * 2 + 1
    if maxPos == i  break
    [a[i], a[maxPos]] = [a[maxPos], a[i]]
    i = maxPos
  }
}

代码中我们是从 n>>1 到 1 进行堆化，也就是说下标为 n/2 + 1 到 n 的节点都是叶子节点，不需要堆化。
建堆的事件复杂度是堆 - 图11 。

2. 排序

建堆结束后，数组中的数据已经是大顶堆了。那么数组的第一个元素就是最大元素。
这时候我们将它与最后一个元素交换，那么最大的元素就放到下标为 n 的位置了。
我们只需要把剩下 n-1 个元素堆化，构建为堆。再取堆顶元素，放到 n -1 位置。
依次直到堆中只剩下下标为 1 的一个元素，排序工作就结束了。

static public sort(a: Array<number>, n: number) {
  this.buildHeap(a, n)
    let k = n
  while (k > 1) {
       [a[1], a[k]] = [a[k], a[1]]
    k--
    heapify(a, k, 1)
  }
}

时间复杂度：建堆：堆 - 图13 ，排序：堆 - 图14
空间复杂度：原地排序算法

前面我们所有的操作都是从下标为 1存储开始处理。
如果是下标为 0 的话，计算子节点和父节点的公式需要调整下，下标为 i 的节点，左子节点的下标是 2 * i + 1 ，右子节点 2 * i + 2 ，父节点的下标是 (i - 1) / 2

代码

TypeScript 在线地址

class Heap {
  a: Array<number>; // 从 1 开始存储数据
  maxCount: number; // 可以存储的最大个数
  count: number; // 已经存储的个数
    constructor(capacity: number) {
    this.a = new Array(capacity + 1)
    this.maxCount = capacity
    this.count = 0
  }
  public insert(data: number) {
    if (this.count >= this.maxCount) return
    this.count++
    this.a[this.count] = data
    let i = this.count
    while ( i >> 1 >0 && this.a[i] > this.a[i>>1]) {
      [this.a[i], this.a[i>>1]] = [this.a[i>>1], this.a[i]]
      i = i>> 1
    }
  }
  public removeMax() {
    if (this.count == 0) return
    this.a[1] = this.a[this.count]
    this.count--
    this.heapify(this.a, this.count, 1)
  }
  private heapify(a: Array<number>, n: number, i :number) {
    while(true) {
      let maxPos:number = i
      if (i * 2 <= n && a[i] < a[i*2]) {
        maxPos = i * 2
      }
      if (i * 2 + 1 <= n && a[maxPos] < a[i*2+1]) {
        maxPos = i * 2
      }
      if (maxPos == i) {
        break
      }
      [a[i], a[maxPos]] = [a[maxPos], a[i]]
      i = maxPos
    }
  }
  private static  heapify(a: Array<number>, n: number, i :number) {
    while(true) {
      let maxPos = i
      if (i * 2 <= n && a[i] < a[i*2]) {
        maxPos = i * 2
      }
      if (i * 2 + 1 <= n && a[maxPos] < a[i*2+1]){
        maxPos = i * 2 + 1
      }
      if (maxPos === i) {
        break
      }
      [a[i], a[maxPos]] = [a[maxPos], a[i]]
      i = maxPos
    }
  }
  public static  buildHeap(a: Array<number>, n :number) {
    for (let i = n >> 1; i >= 1; i--) {
      Heap.heapify(a, n, i)
      }
  }
  public static  sort(a: Array<number>, n:number) {
       Heap.buildHeap(a, n)
    let k = n
    while (k > 1) {
      [a[1], a[k]] = [a[k], a[1]]
      k--
      Heap.heapify(a, k, 1)
    }
  }
}
let arr = [0, 15,9,5,6,7,8,1,2,33, 17, 21, 16,13]
// let hp = new Heap(arr.length + 1)
// for (let val of arr) {
//   hp.insert(val)
// }
// console.log(hp.a)
// hp.insert(22)
// console.log(hp.a)
// hp.removeMax()
// console.log(hp.a)
Heap.buildHeap(arr, 3)
console.log(arr)
// Heap.sort(arr,13)
// console.log(arr)

go 在线地址

package main
import (
    "fmt"
)
type heap struct {
    a []int // 从 1 开始
    count int
}
func buildHeap(a []int) *heap {
    n := len(a) -1
    for i:= n >> 1; i>= 1; i-- {
        heapify(a, n, i)
    }
    return &heap{a, n}
}
func sortHeap(a []int)[]int {
    hp := buildHeap(a)
    k := len(hp.a) -1
    for k > 1 {
        hp.a[1], hp.a[k] = hp.a[k], hp.a[1]
        k --
        heapify(hp.a, k, 1)
    }
    return a
}
func (hp *heap)Push(data int) {
    hp.count++
    hp.a = append(hp.a, data)
    i := hp.count
    for i>> 1 > 0 && hp.a[i] > hp.a[i>>1] {
        hp.a[i], hp.a[i>>1] = hp.a[i>>1], hp.a[i]
        i = i >> 1
    }
}
func (hp *heap)Pop() int {
    if len(hp.a) < 1 {
        return -1
    }
    out := hp.a[1]
    hp.a[1] = hp.a[hp.count]
    hp.count--
    heapify(hp.a, hp.count, 1)
    return out
}
func heapify(a []int, n, i int) {
    for {
        maxPos := i
        if i * 2 <=n && a[i*2] > a[i] {
            maxPos = i * 2
        }
        if i * 2 +1 <= n && a[i*2+1] > a[maxPos] {
            maxPos = i * 2+1
        }
        if maxPos == i {
            break
        }
        a[i], a[maxPos] = a[maxPos], a[i]
        i = maxPos
    }
}
func main() {
    arr := []int{0, 15,9,5,6,7,8,1,2,33, 17, 21, 16,13}
    fmt.Println(sortHeap(arr))
    hp := buildHeap(arr)
    fmt.Println(hp.a)
    hp.Push(34)
    fmt.Println(hp.a)
    top :=hp.Pop()
    fmt.Println(top, hp.a)
}