KMP算法发明人 Knuth 大佬如是说：思路很简单，细节是魔鬼。

二分查找真正的坑在于到底要给 **mid** 加一还是建议，循环条件中到底使用 **<=** 还是 **<** 。

  1. 搜索一个元素时        搜索区间两端闭
  2. while 条件带等号     否则需要打补丁
  3. if 相等就返回       其他的事甭操心
  4. mid 必须加减一     因为区间两端闭
  5. while 结束就凉了     凄凄惨惨返 -1
  7. 搜索左右边界时     搜索区间要阐明
  8. 左闭右开最常见        其他逻辑便自明
  9. while 要用小于号     这样才能不漏掉
  10. if 相等别返回     利用 mid 锁边界
  11. mid 加一或减一？    要看区间开或闭
  12. while 结束不算晚     因为你还没返回
  13. 索引可能出边界           if 检查保平安
  15. 左闭右开最常见        难道常见就合理？

二分查找最常见的几个场景：

  • 查找一个数
  • 查找左边界
  • 查找右边界

二分查找框架

  1. func binarySearch(nums []int, target int) {
  2.     left, right := 0, ...
  4.     for ... {
  5.         mid := left + (right - left) / 2
  6.         if nums[mid] == target {
  7.             ...
  8.         } else if nums[mid] < target {
  9.             left = ...
  10.         } else if nums[mid] > target {
  11.             right = ...
  12.         }
  13.     }
  14.     return ...
  15. }

二分查找的一个技巧是：不要出现 else，所有情况都用 else if 写清楚，这样可以清楚地展现所有细节。
在后续理解之后，可以自行简化。
注意：防止 mid 计算时 left 和 right 太大直接相加会溢出，所以使用 left + (right-left)/2 就和 (left + right) / 2 是一样的，当然也可以使用 left + (right - left) >> 1 都是一样的效果。

寻找一个数

搜索一个数，如果存在，返回其索引，否则返回 -1

  1. func binarySearch(nums []int, target int) int {
  2.     left, right := 0, len(nums)-1 // 注意
  4.     for left <= right {
  5.         mid := left + (right - left) / 2
  6.         if nums[mid] == target {
  7.             return mid
  8.         } else if nums[mid] < target {
  9.             left = mid + 1 // 注意
  10.         } else if nums[mid] > target {
  11.             right = mid - 1 // 注意
  12.         }
  13.     }
  14.     return -1
  15. }

于是几个小问题

1. 为什么 for 循环的条件是 <= ，而不是 < ？

因为 right 初始化的赋值是 len(nums)-1 ，即最后一个元素的索引，而不是 len(nums) 。
这两种可能出现在不同功能的二分查找中，区别是，前者相当于两端都是闭区间 [left, right] ，后者相当于 [left, right) ，因为索引大小为 len(nums) 是越界的。
这里我们使用的是 **[left, right]** 两端都闭的区间，这个区间也就是每次进行搜索的区间。
什么时候停止搜索呢？当然是找到目标时可以终止。还有就是退出循环的时候，表示没找到。搜索区间为空的时候应该退出循环，表示没找到。
for left <= right 的终止条件是 left == right + 1 ，用区间的形式就是 [right + 1, right] ，所以这时候区间为空。

for left < right 的终止条件是 left == right ，用区间的形式是 [right, right] ，这时候区间非空，还有一个 right 值被忽略，如果这时候循环终止，索引 right 会被漏掉，这时候直接返回 -1 是错误的。

所以，这种情况如果非要使用 for left < right 的话，需要打两个补丁：

  1. right = len(nums) // 注意因为区间是 `[left,right)`，所以要从 len(nums) 开始，否则从 len(nums) - 1 就会少掉最后一个值。 
  3. if nums[left] == target {
  4.     return left
  5. } else {
  6.     return -1
  7. }

2. 为什么 left = mid +1 , right = mid -1 ？有些代码是 right = mid 或者是 left = mid ，有什么区别？

前面明确了搜索区间后，本题的搜索区间是两端闭合的，即 [left, right] ，当我们发现 mid 不是我们要找的 target 时，下一步肯定是要搜索 [left, mid -1] 或 [mid + 1, right] ，因为 **mid** 已经搜索过，应该从搜索区间中去除。

3. 缺陷？

这个算法实际上是有局限性的。
举个栗子，有序数组 nums = [1,2,2,2,3] ， target 为 2，此算法返回的索引是 2，没错。
但是如果我想得到 target 的左边界，即索引 1 ，或者是右边界，索引 3 。

也许，你会说找到一个 target ，然后向左或向右线性搜索不行吗？可以，但是不好，因为这样难以保障二分查找对数级的复杂度了。

寻找左侧边界的二分查找

  1. func leftBound (nums []int, target int) int {
  2.     if len(nums) == 0 {
  3.         return -1
  4.     }
  5.     left, right := 0, len(nums) // 注意
  7.     for left < right { // 注意
  8.         mid := left + (right - left) / 2
  9.         if nums[mid] == target {
  10.             right = mid
  11.         } else if nums[mid] < target {
  12.             left = mid + 1
  13.         } else if nums[mid] > target {
  14.             right = mid // 注意
  15.         }
  16.     }
  17.     return left
  18. }

1. 为什么 for 循环条件中是 < ，而不是 <= ?

同上分析， right = len(nums) ，相当于每次循环的搜索区间是 [left, right) 左闭右开。
for left < right 的终止条件是 left == right ，此时搜索区间是 [left, left) 为空，所以可以正确终止。

2. 为什么最后没有返回 -1 的操作？如果 nums 中没有 target 这个值，怎么办？

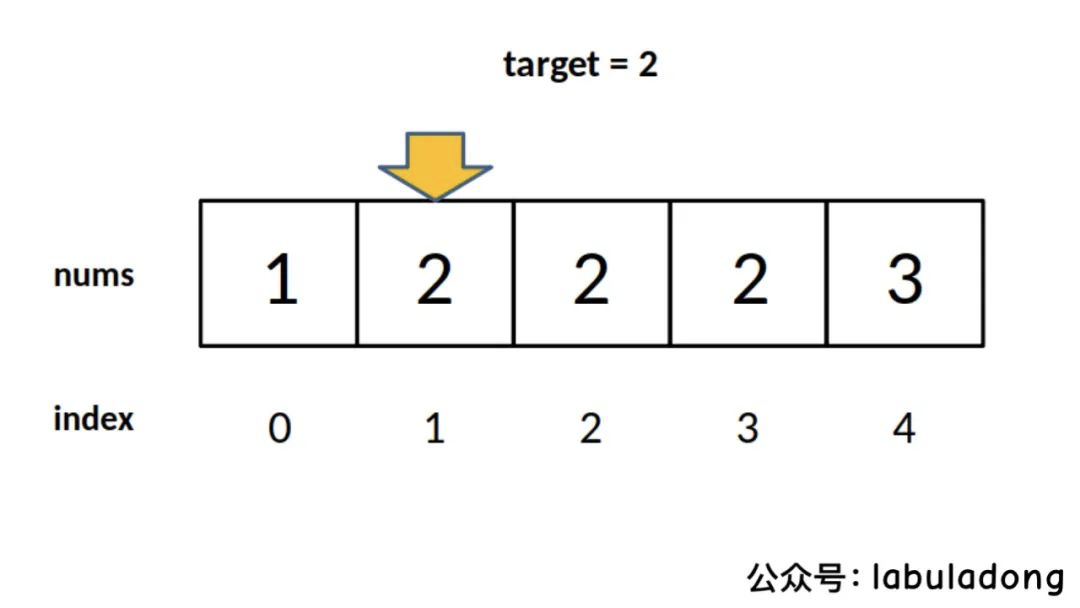
image.png
左侧边界怎么理解呢？
对于上面数组，算法返回1， 这个 1 可以理解为 nums 中小于 2 的元素有 1 个。
nums = [2,3,5,7], target = 1 算法返回 0， 表示 nums 小于 1 的有 0 个。
nums = [2, 3, 5, 7], target = 8 算法返回 4， 表示 nums 小于 8 的有 4个。

综上，函数返回值（也就是这个 left ）的取值区间是 [0, len(nums)] ，所以我们可以加一个补丁：

  1. for (left < right){
  2.     //...
  3. }
  4. // 返回数组长度，表示target比所有数都大
  5. if left == len(nums) {
  6.     return -1
  7. } 
  8. // 类似前面的补丁
  9. if nums[left] == target {
  10.     return left
  11. } else {
  12.     return -1
  13. }

3. 为什么 left = mid + 1, right = mid 和之前的算法不一样？

我们搜索的区间是 [left, right) 左闭右开，所以当 nums[mid 被检测后，下一步的搜索区间应该是去掉 mid 的两个区间，也就是 [left, mid) 和 [mid + 1, right) 。

4. 为什么该算法能够搜索左侧边界？

主要是 nums[mid] == target 的处理：

  1. if nums[mid] == target {
  2.     right = mid
  3. }

找到 target 时不要立即返回，而是缩小 搜索区间的上界 right ，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。

5. 为什么返回 left 而不是 right ？

因为 for 循环的退出条件是 left == right ，所以都一样。

6. 为什么不能把 right 改为 len(nums)-1 ，也就是继续使用两边都是闭的搜索区间？

当然可以使用，但是需要理解搜索区间的概念。有效避免漏掉元素。
因为改为双闭区间，所以 right 是 len(nums)-1 ，那么 for 循环的终止条件是 left == right + 1 ，也就是 left <= right 。

  1. func leftBound(nums []int, target int) int {
  2.     left, right := 0, len(nums)-1
  4.     for left <= right {
  5.         mid := left + (right - left) / 2
  6.         if nums[mid] < target {
  7.             // [mid +1, right]
  8.             left = mid + 1
  9.         } else if nums[mid] > target {
  10.             // [left, mid - 1]
  11.             right = mid -1
  12.         } else if nums[mid] == target {
  13.             // 收缩右边界
  14.             right = mid -1
  15.         }
  16.     }
  17.     // 检测边界
  18.     // ...
  19. }

由于 退出循环是 left == right +1 ，可能存在 target 比 nums 中所有元素都大时， 索引越界的情况。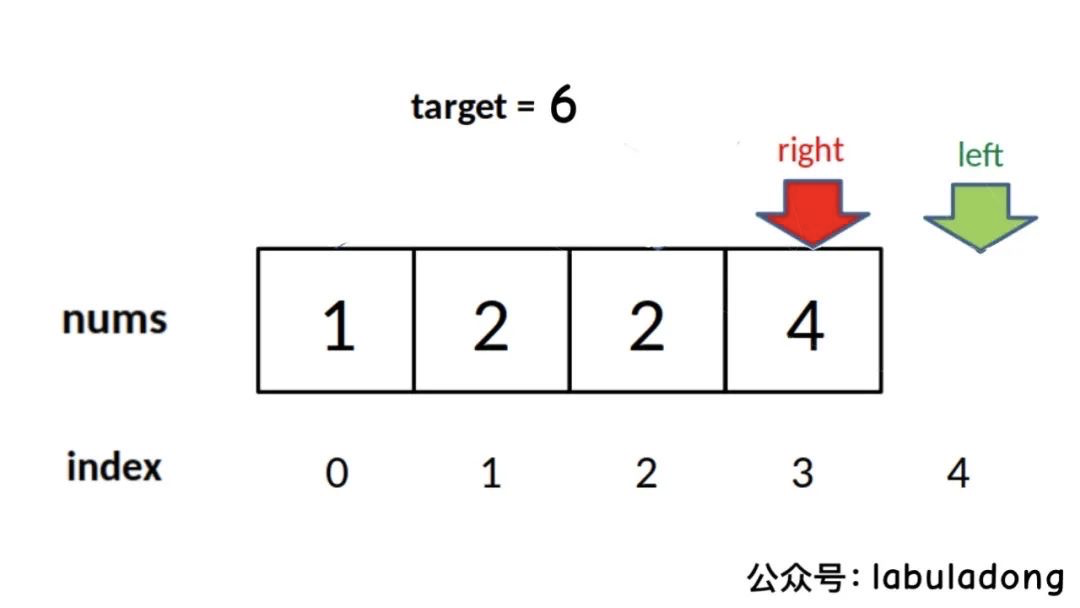
image.png

  1. func leftBound(nums []int, target int) int {
  2.     left, right := 0, len(nums)-1
  4.     for left <= right {
  5.         mid := left + (right - left) / 2
  6.         if nums[mid] < target {
  7.             // [mid +1, right]
  8.             left = mid + 1
  9.         } else if nums[mid] > target {
  10.             // [left, mid - 1]
  11.             right = mid -1
  12.         } else if nums[mid] == target {
  13.             // 收缩右边界
  14.             right = mid -1
  15.         }
  16.     }
  17.     if left >= len(nums) {
  18.         return -1
  19.     }
  20.     if nums[left] == target {
  21.         return left
  22.     } else {
  23.         return -1
  24.     }
  25. }

这样，就跟第一种二分搜索算法统一，都是两端都闭的搜索区间了，最后返回值也都是 left 的值。

寻找右侧边界的二分查找

常见的左闭右开写法

  1. func rightBound(nums []int, target int) {
  2.     if len(nums) == 0 {
  3.         return -1
  4.     }
  5.     left, right := 0, len(nums)
  6.     for left < right {
  7.         mid := left + (right - left) /2
  8.         if nums[mid] == target {
  9.             left = mid + 1
  10.         } else if nums[mid] > target {
  11.             right = mid
  12.         } else if nums[mid] < target {
  13.             left = mid + 1
  14.         }
  15.     }
  16.     return left -1 
  17. }

1. 为什么这个算法能找到右边界？

  1. if nums[mid] == target {
  2.     left = mid + 1
  3. }

当 nums[mid] == target 时，不要立即返回，而是增大搜索区间的左侧 left ，使得区间不断向右收缩，从而达到锁定右边界的目的。

2. 为什么是 left = mid+1, right = mid ？

因为这里是 [left, right) 左闭右开区间，所以我们的循环退出条件是 left == right 。
故当 mid 已经检测完后，我们需要做的是检测 [left, mid) 和 [mid + 1, right) 。

3. 为什么最后返回 left -1 而不是直接返回 left ?

循环的终止条件是 left == right ，所以 right 和 left 是一样的。
为什么减一是因为 搜索右边界的一个特殊点：

  1. if nums[mid] == target {
  2.     left = mid + 1;
  3.     // 这样想: mid = left - 1
  4. }

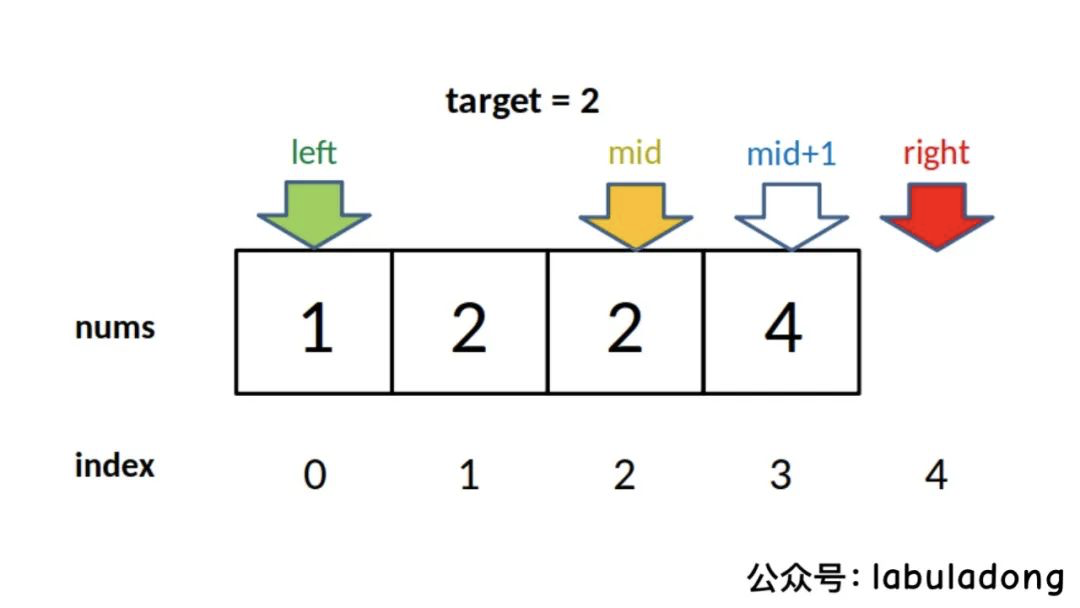
image.png
由于对于 left 的更新是 left = mid + 1 ，也就是在退出循环时， nums[left] 不一定等于 target 了，而 nums[left -1] 可能是 target 。

4. 为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，咋办？

类似前面的左边界搜索，因为退出循环的条件是 left == right ，也就是说 left 的取值返回是在 0, len(nums) 。

  1. for left < right {
  2.     //...
  3.     if  left == 0 {
  4.         return -1
  5.     }
  6.     if nums[left -1] == target {
  7.         return left -1
  8.     } else {
  9.         return -1
  10.     }
  11. }

5. 能够改成两端闭合的搜索区间呢？

  1. func rightBound(nums []int, target int) int {
  2.     left, right := 0, len(nums)-1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] == target {
  6.             left = mid + 1
  7.         } else if nums[mid] > target {
  8.             right = mid -1
  9.         } else if nums[mid] < target {
  10.             left = mid +1
  11.         }
  12.     }
  14.     if right <0 {
  15.         return -1
  16.     }
  17.     if nums[right] == target {
  18.         return right
  19.     } else {
  20.         return -1
  21.     }

当target比所有元素都小时，right会被减到 -1，所以需要在最后防止越界：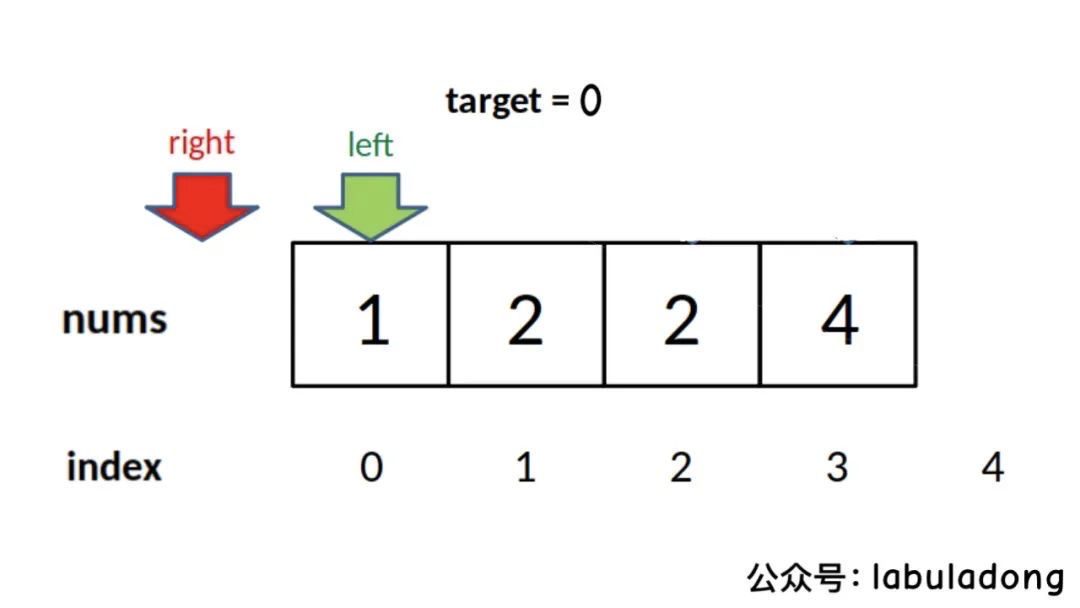
image.png

逻辑统一

最基本的二分查找算法 ：

  • 因为初始化 right = len(nums)-1 ，决定了搜索区间是 [left, right] （双闭区间）
  • 循环退出条件 for left <= right 即 left = right + 1
  • 每次当 mid 排除后，搜索区间为 [left, mid - 1) 或 [mid + 1, right) 即 left = mid + 1 right = mid - 1
  • 因为我们只需要找一个 target 索引，所以当 nums[mid] == target 立即返回即可

寻找左侧边界的二分查找：

  • 因为初始化 right = len(nums) ，决定了搜索区间是 [left, right) （左开右闭）
  • 循环退出条件 for left < right 即 left = right
  • 每次当 mid 排除后，搜索区间为 [left, mid) 或 [mid + 1, right) 即 left = mid + 1 right = mid
  • 因为我们需要找到左边界，所以当 nums[mid] == target 时不要立即返回，要收紧右边界以锁定左边界 **right = mid**
  • 由于找的是左边界，可能存在所有的元素都小于 target 的情况，所以还要根据 left 是否越界，来判断返回值
  • 由于最后退出条件是 left = right ，导致 [left, left) ，所以left 索引对应的值是否是 target 没有判断，所以要补充一下

寻找右侧边界的二分查找：

  • 因为初始化 right = len(nums) ，决定了搜索区间是 [left, right) （左开右闭）
  • 循环退出条件是 for left < right 即 left = right
  • 每次当 mid 排除后，搜索区间为 [left, mid) 或 [mid + 1, right) 即 left = mid + 1 right = mid
  • 因为我们需要找到右边界，所以当 nums[mid] == target 时不要立即返回，要收紧左边界以锁定右边界 **left = mid + 1**
  • 由于找的是右边界，可能存在所有的元素都大于 target 的情况，所以还要根据 left 是否越界，来判断返回值
  • 由于最后退出条件是 left = right ，导致 [left, left) ，但是由于 **left = mid + 1** 的操作，所以是 **left - 1** 索引对应的值是否是 target 没有判断，所以要补充一下

我们可以把所有的 搜索区间都统一为两端都闭：

  1. func binarySearch (nums []int, target int) int {
  2.     left, right := 0, len(nums)-1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.          if nums[mid] > target {
  6.             right = mid -1
  7.         } else if nums[mid] < target {
  8.             left = mid + 1
  9.         } else if nums[mid] == target {
  10.             return mid
  11.         } 
  12.     }
  13.     return -1
  14. }
  16. func leftBound(nums []int, target int) int {
  17.     left, right := 0, len(nums) - 1
  18.     for left <= right {
  19.         mid := left + (right - left) >> 1
  20.         if nums[mid] > target {
  21.             right = mid -1
  22.         } else if nums[mid] < target {
  23.             left = mid + 1
  24.         }else if nums[mid] == target {
  25.             right = mid -1
  26.         }
  27.     }
  28.     // 因为我们要找左边界，所以检测左侧越界情况，同时最后也是返回左边界
  29.     if left >= len(nums) {
  30.         return -1
  31.     }
  32.     if  nums[left] != target {
  33.         return -1
  34.     } else {
  35.         return left
  36.     }
  37. }
  39. func rightBound(nums []int, target int) int {
  40.     left, right := 0, len(nums) - 1
  41.     for left <= right {
  42.         mid := left + (right - left) >> 1
  43.         if nums[mid] > target {
  44.             right = mid -1
  45.         } else if nums[mid] < target {
  46.             left = mid + 1
  47.         } else if nums[mid] == target {
  48.             left = mid + 1
  49.         }
  50.     }
  51.     // 因为我们是要找右边界，所以要检测右边界越界情况，同时最后也是返回右边界
  52.     if right < 0 {
  53.         return -1
  54.     }
  55.     if  nums[right] != target {
  56.         return -1
  57.     } else {
  58.         return right
  59.     }
  60. }

补充

查找第一个值等于给定值的元素

可以理解为查找左边界

  1. func leftBound(nums [] int, target int) int {
  2.     left, right := 0, len(nums) - 1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] >= target {
  6.             right = mid -1
  7.         } else {
  8.             left = mid + 1
  9.         }
  10.     }
  12.     // 注意检测 左边界是否越界
  13.     // 顺便解释下这里为什么要判断是否 nums[left] 与 targe 的相等关系
  14.     // 因为前面的时候是 >= 的时候收缩右边
  15.     // 所以如果不加这个判断得到的只能是第一个大于等于给定值的元素
  16.     // eg: [5,7,7,8,8,10] 6 不加这个判断的话会返回 1
  17.     if left >= len(nums) || nums[left] != target {
  18.         return -1
  19.     }
  20.     return left
  21. }

王铮的课中讲到另一种解法

  1. func leftBound(nums [] int, target int) int {
  2.     left, right := 0, len(nums) - 1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] > target {
  6.             right = mid -1
  7.         } else if nums[mid] < target {
  8.             left = mid + 1
  9.         } else {
  10.             // 判断是不是第一个，或者前一个元素不是 target，均表示已经是左边界了
  11.             if mid == 0 || a[mid -1] != target {
  12.                 return mid
  13.             }
  14.             right = mid - 1
  15.         }
  16.     }
  18.     return -1
  19. }

查找最后一个值等于定值的元素

可以理解为查找右边界

  1. func rightBound(nums []int, target int) int {
  2.     left, right := 0, len(nums) -1
  3.     for left < right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] <= target {
  6.             left = mid + 1
  7.         } else {
  8.             right = mid -1
  9.         }
  10.     }
  12.     // 注意检测右边界是否越界
  13.     // 顺便解释下这里为什么要判断是否 nums[right] 与 targe 的相等关系
  14.     // 因为前面的时候是 <= 的时候收缩左边
  15.     // 所以如果不加这个判断得到的只能是最后一个小于等于给定值的元素
  16.     // eg: [5,7,7,8,8,10] 6 不加这个判断的话会返回 0
  17.     if right < 0 || nums[right] != target {
  18.         return -1
  19.     }
  20.     return right
  21. }

王铮的课里提到了另一种解法

  1. func rightBound(nums []int, target int) int {
  2.     left, right := 0, len(nums) -1
  3.     for left < right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] < target {
  6.             left = mid + 1
  7.         } else if nums[mid] > target {
  8.             right = mid -1
  9.         } else {
  10.             // 当前 mid 是否是最后一个节点或 下一个节点不等于 target 
  11.             if mid == len(nums) -1 || nums[mid + 1] != target {
  12.                 return mid
  13.             }
  14.             left = mid + 1
  15.         }
  16.     }
  17.     return -1
  18. }

查找第一个大于等于给定值的元素

查找大于等于给定值的左边界

  1. func leftBound(nums [] int, target int) int {
  2.     left, right := 0, len(nums) - 1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] >= target {
  6.             // 收缩右边界
  7.             right = mid -1
  8.         } else {
  9.             left = mid + 1
  10.         }
  11.     }
  13.     // 注意左边界越界
  14.     if left >= len(nums) || nums[left] < target {
  15.         return -1
  16.     }
  17.     return left
  18. }

王铮课里提到的另一种解法：

  1. func leftBound(nums [] int, target int) int {
  2.     left, right := 0, len(nums) - 1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] >= target {
  6.             // 注意判断是否是第一个值，或者前一个值不等于 target
  7.             if mid == 0 || nums[mid - 1] < target {
  8.                 return mid 
  9.             }
  10.             right = mid -1
  11.         } else {
  12.             left = mid + 1
  13.         }
  14.     }
  16.     return -1
  17. }

查找最后一个小于等于给定值的元素

查找小于等于给定值的右边界

  1. func rightBound(nums []int, target int) int {
  2.     left, right := 0, len(nums) -1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.         if num[mid] <= target {
  6.             // 收缩左边界
  7.             left = mid + 1
  8.         } else {
  9.             right = mid -1
  10.         }
  11.     }
  13.     // 判断右边界越界情况
  14.     if right < 0 || nums[right] > target {
  15.         return -1
  16.     }
  17.     return right 
  18. }

王铮的课里提到了另一种解法

  1. func rightBound(nums []int, target int) int {
  2.     left, right := 0, len(nums) -1
  3.     for left <= right {
  4.         mid := left + (right - left) >> 1
  5.         if nums[mid] <= target {
  6.             // 右边界，所以判断是否是最后一个节点，或下一个节点是否满足条件
  7.             if mid == len(nums) - 1|| nums[mid +1] > target {
  8.                 return mid
  9.             }
  10.             left = mid + 1
  11.         } else {
  12.             right = mid -1
  13.         }
  14.     }
  16.     return -1
  17. }