二叉搜索树查缺补漏

BST 的合法性

由于 BST 需要满足以下条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

按照我们前面的理解是不是就会写出来

func isValidBST(root *TreeNode) bool {
    if root == nil {
        return true
    }
    if root.Left != nil && root.Val < root.Left.Val {
        return false
    }
    if root.Right != nil && root.Val > root.Right.Val {
        return false
    }
    return isValidBST(root.Left) && isValidBST(root.Right)
}

需要注意这个算法里，只考虑到了父子节点的大小问题，没有考虑到祖孙节点的比较。
BST 需要的是 root 的所有左子树节点的值都小于 root.Val ， 所有右子树节点的值都要大于 root.Val 。
所以可以引入

func isValidBST(root *TreeNode, min *TreeNode, max *TreeNode) bool {
    if root == nil  {
        return true
    }
    if min != nil && root.Val < min.Val {
        return false
    }
    if max != nil && root.Val > max.Val {
        return false
    }
    return isValidBST(root.Left, nil, root) && isValidBST(root.Right, root, nil)    
}

这里的 min 和 max 不需要理解，只需要记住他们的作用是用来限制最大值和最小值的。
然后记住左子树的节点值都比 root.Val 小，右子树的节点都比 root.Val 大即可。

BST 中搜索一个数

func isInBST(root *TreeNode, target int) bool {
    if root == nil {
        return false
    }
    if root.Val == target {
        return true
    }
    return isInBST(root.Left, target) || isInBST(root.Right,target)
}

这么写相当于穷举了所有的节点，适用于普通的二叉树。那么对于 BST 我们应该利用 左小右大 的特性。

func isInBST(root *TreeNode, target int) bool {
    if root == nil {
        return false
    }
    if root.Val == target {
        return true
    }
    if root.Val < target {
        return isInBST(root.Right, target)
    }
    if root.Val > target {
        return isInBST(root.Left, target)
    }
}

BST 中插入一个数

这里需要理解为什么要生成新的节点

func insertIntoBST(root *TreeNode, val int) *TreeNode{
    if root == nil {
        return &TreeNode{Val: val}
    }
    if root.Val < val {
        root.Right = insertIntoBST(root.Right, val)
    }
    if root.Val > val {
        root.Left = insertIntoBST(root.Left, val)
    }
    return root
}

BST 中删除一个数

删除一个节点时可能会触发这三种情况：

• 删除的节点正好是末端节点，没有子节点
• 删除节点存在一个子节点
• 删除节点存在两个子节点

其中第三个比较麻烦，为了不破坏 BST 的特性，A 必须找到左子树中最大的那个节点 或右子树中最小的节点来接替自己。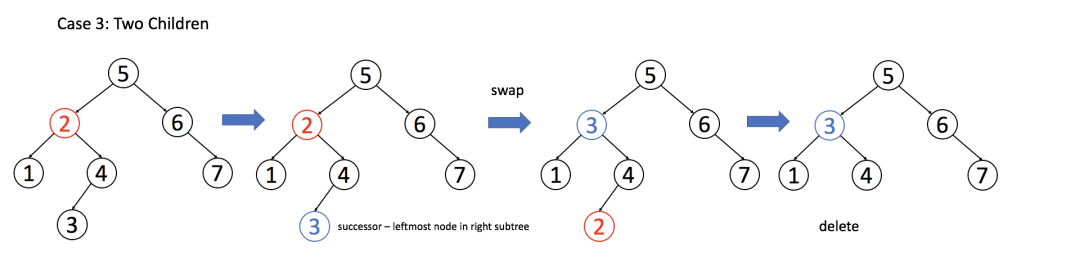

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func deleteNode(root *TreeNode, key int) *TreeNode {
    if root == nil {
        return root
    }
    if root.Val == key {
        if root.Left == nil {
            return root.Right
        }
        if root.Right == nil {
            return root.Left
        }
        minNode := func(node *TreeNode) *TreeNode {
            for node.Left != nil {
                node = node.Left
            }
            return node
        }(root.Right)
        minNode.Left = root.Left
        root = root.Right
    } else if root.Val > key {
        root.Left = deleteNode(root.Left, key)
    } else {
        root.Right = deleteNode(root.Right, key)
    }
    return root
}