DP 学习 - 《数据结构和算法知识》

斐波那契数列
凑零钱问题
总结

动态规划问题一般形式都是求最值（运筹学的一种最优方法），例如求最长递增子序列，最小编辑距离。
核心问题是穷举。
动态规划的穷举，存在重叠子问题，暴力穷举会导致效率极低，需要借助备忘录或 DP table 来优化穷举过程。
具备最优子结构，才能通过子问题的最值得到原问题的最值
穷举所有可行解不是一件容易的事，需要列出正确的状态转移方程。

动态规划三要素：重叠子问题、最优子结构、状态转移方程。
其中状态转移方程最为困难，有个思维框架：

明确 base case
明确状态
明确选择
定义 DP 数组/函数的含义

# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

斐波那契数列

通常我们会写出来：

package main
func fib(n int) int {
    if n <= 2 {
        return 1
    }
    return fib(n-1) + fib(n-2)
}

注：凡递归的问题，最好画出递归树，有助于分析算法复杂度，寻找算法低效的原因。
举个栗子如果是 fib(20) 的话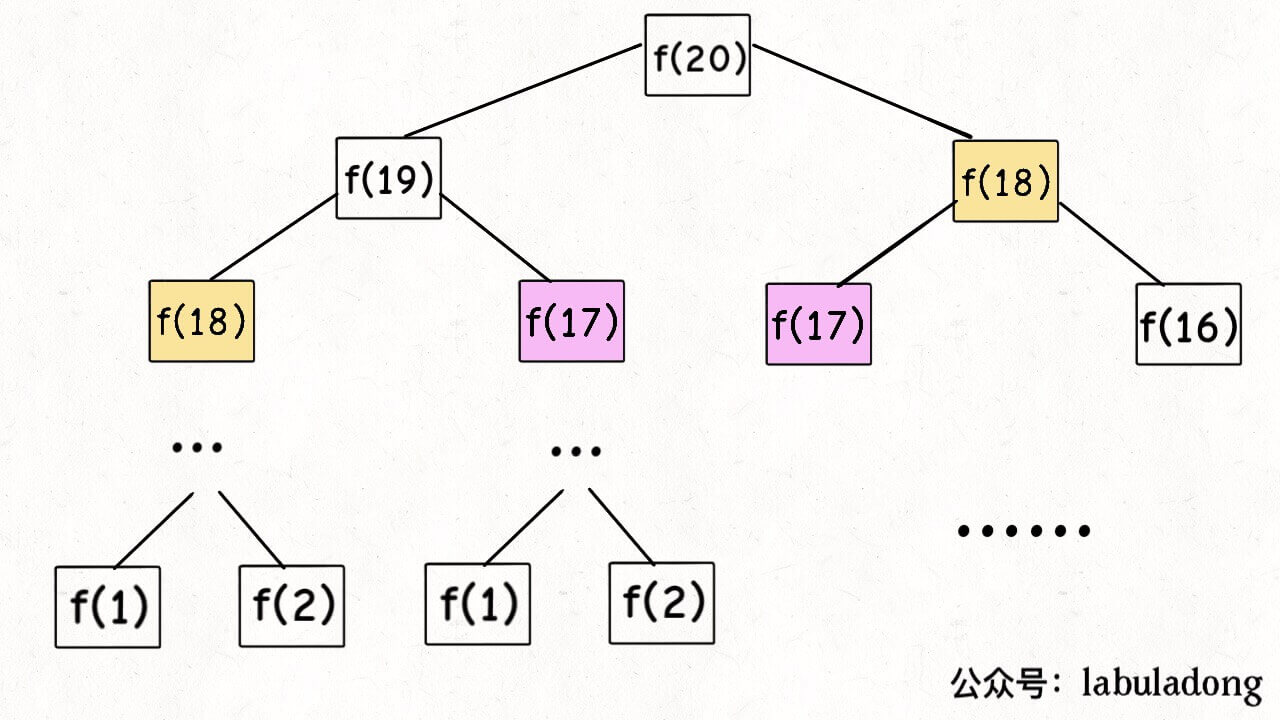

递归算法的时间复杂度怎么计算呢？就是用子问题个数乘以解决子问题需要的时间。

子问题个数，即递归树中节点总数，显然这里是指数级的，故是个
解决单个子问题的时间，这里没有循环，只有 fib(n-1)+fib(n-2) ，所以是。

所以这个算法的时间复杂度是 DP 学习 - 图4 ，指数级别。
通过递归树，明显发现其中存在大量的重复计算。

这就是动态规划问题的第一个性质：重叠子问题。

带备忘录的递归解法

每次计算一个子问题的答案后先别着急返回，存到备忘录中再返回
每次计算子问题时，先去备忘录里查，如果发现解决过问题，就可以直接把答案拿出来，不用再耗时计算了

package main
import "fmt"
func fib(n int) int {
    if n < 1 {
        return 0
    }
    var memo = make([]int, n+1)
    return helper(memo, n)
}
func helper(memo []int, n int) int {
    if n <= 2 {
        return 1
    }
    if memo[n] != 0 {
        return memo[n]
    }
    memo[n] = helper(memo, n-1) + helper(memo, n-2)
    return memo[n]
}
func main() {
    fmt.Println(fib(0))
}

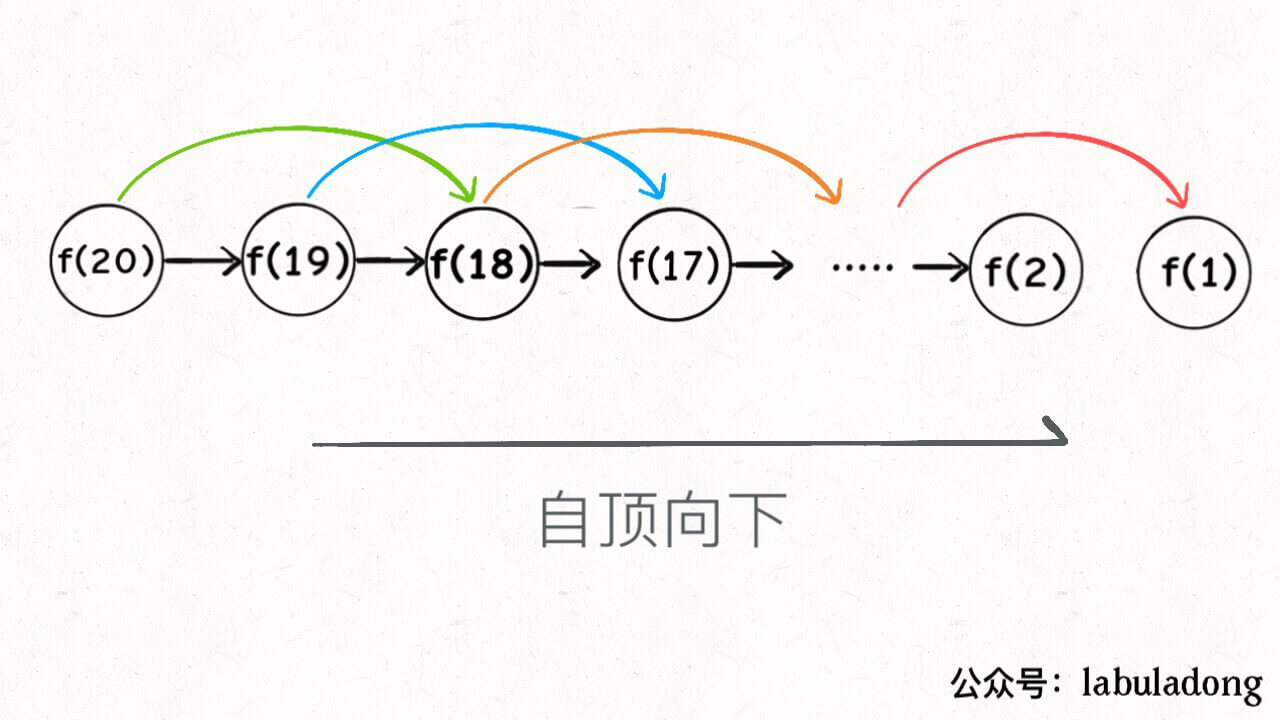
这时候的时间复杂度是 DP 学习 - 图6
这种解法是自顶向下，动态规划是自底向上。
怎么理解自顶向下呢？
递归树中，从上往下延伸，都是从一个规模较大的原问题如 f(20) 向下逐渐分解规模，直到 f(1) 和 f(2) 这种 base case，然后逐层返回答案。
那么自底向上呢？

标准 DP

我们直接从最底下，最简单、规模最小的问题 f(1) 和 f(2) 往上推，直到我们需要的问题，这就是动态规划的思路。

package main
import "fmt"
func fib(n int) int {
    if n < 1 {
        return 0
    }
    if n <= 2 {
        return 1
    }
    var dp = make([]int, n+1)
    dp[1], dp[2] = 1, 1
    for i := 3; i <= n; i++ {
        dp[i] = dp[i-1] + dp[i-2]
    }
    return dp[n]
}
func main() {
    fmt.Println(fib(10))
}

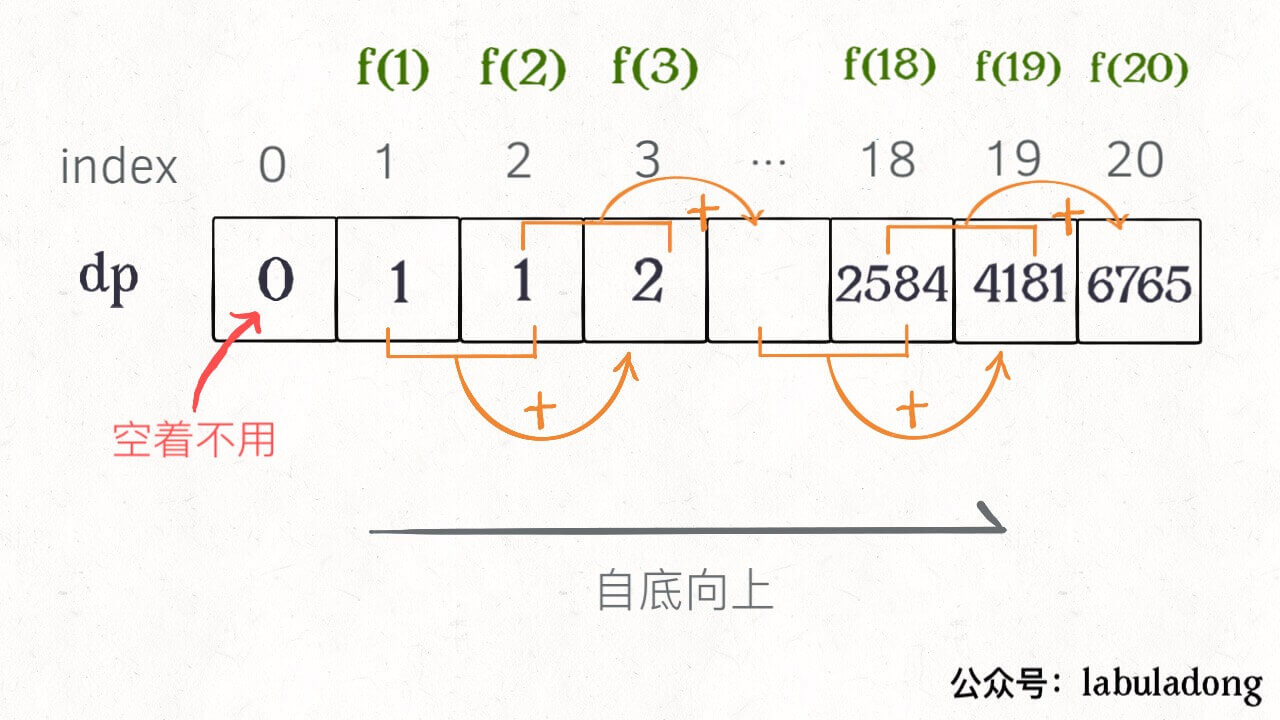
这里就可以引申出状态转移方程了，实际上就是描述问题结构的数学形式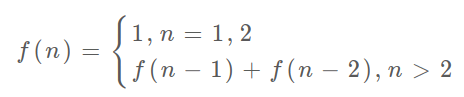

怎么理解状态转移方程呢。举个栗子就是把 f(n) 想做状态 n ，这个状态 n 是由状态 n-1 和状态 n-2 相加转移而来的。

千万不要看不起暴力解法，动态规划问题最困难的就是写出这个暴力解法，即状态转移方程。

状态压缩

到了这里斐波那契数还有最后一个优化点，实际上当前状态只跟前两个状态有关，所以完全不需要使用 DP Table 来记录所有状态。

package main
import "fmt"
func fib(n int) int {
    if n < 1 {
        return 0
    }
    if n <= 2 {
        return 1
    }
    prev, curr := 1, 1
    for i := 3; i <= n; i++ {
        sum := prev + curr
        prev = curr
        curr = sum
    }
    return curr
}
func main() {
    fmt.Println(fib(10))
}

这就是状态压缩，当我们发现每次状态转移只需要 DP table 中的一部分是，那么可以尝试使用状态压缩来缩小 DP Table 的大小，只记录有必要的数据。

凑零钱问题

给你 k 种面值的硬币，面值分别为 c1, c2 ... ck，每种硬币的数量无限，再给一个总金额 amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。算法的函数签名如下：

// coins 中是可选硬币面值，amount 是目标金额
int coinChange(int[] coins, int amount);

比如说 k = 3，面值分别为 1，2，5，总金额 amount = 11。那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

暴力递归

要符合最优子结构，子问题必须相互独立。
那么如何列出正确的状态转移方程：

确定 base case：很简单， amount 为 0 的时候返回 0，即不需要任何硬币就已经凑够了目标金额。
明确状态，即原问题和子问题中会变化的变量：由于硬币数量是无线的，面额也是题目中给定的，只有目标金额是不断向 base case 靠近的，所以唯一的状态就是 amount
确定选择，也就是导致状态产生变化的行为：目标金额为什么会变化，因为每选择一枚硬币，就相当于减少了目标金额。所以所有硬币的面值，就是你的选择。
明确 DP 函数/数组的定义：自顶向下解法，会有一个递归的 dp 函数，一般来说函数的参数就是状态转移中会变化的量，也就是状态，函数的返回值就是题目要求我们计算的量。所以 dp(n) 的定义：输入一个目标金额 n ，返回凑出目标金额 n 的最少硬币数 ```go // 伪代码 func coinChange(coins: []int, amount: int) { // 定义：要凑出金额 n，至少要 dp(n) 个硬币 func dp(n:int) {
```
 // base case
 if n == 0 {return 0}
 if n < 0 {return -1}
 // 求最小值，所以初始化为正无穷
 res = float('INF')
 // 做选择，选择需要硬币最少的那个结果
 for coin := range coins {
     subproblem = dp(n - coin)
     # 子问题无解，跳过
     if subproblem == -1: continue
     res = min(res, 1 + subproblem)
 }
 return res if res != float('INF') else -1
```
} return dp(amount) }

状态转移方程是：<br />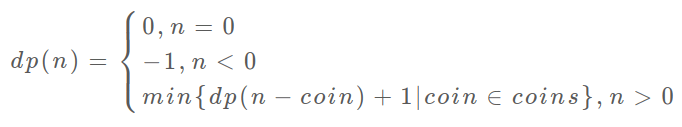![image.png](https://cdn.nlark.com/yuque/0/2021/png/594949/1623400209471-637d1114-099f-461d-b124-fcefb8ef7bff.png#crop=0&crop=0&crop=1&crop=1&height=127&id=zJAP1&margin=%5Bobject%20Object%5D&name=image.png&originHeight=127&originWidth=682&originalType=binary&ratio=1&rotation=0&showTitle=false&size=12021&status=done&style=none&title=&width=682)
比如 `amount = 11, coins = {1,2,5}` 时画出递归树看看：<br />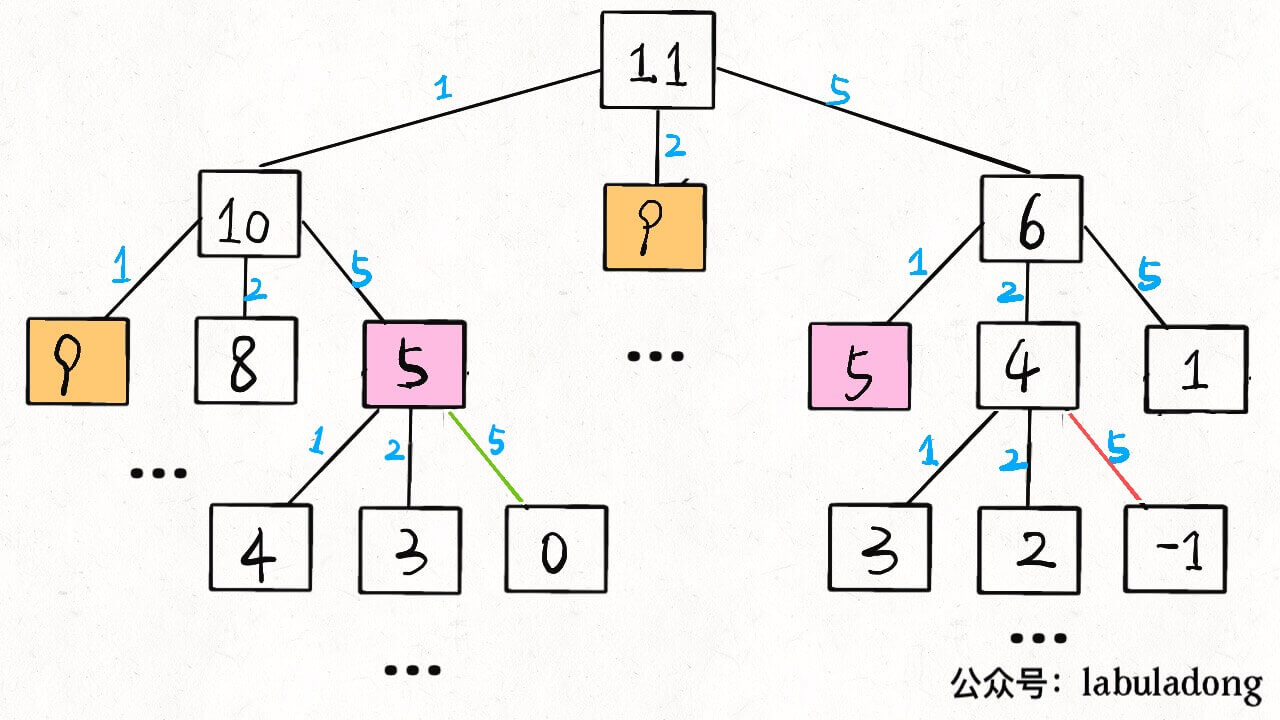![image.png](https://cdn.nlark.com/yuque/0/2021/png/594949/1623400446762-3790cdb0-b953-4430-b2a6-d1a0c1e1a17e.png#crop=0&crop=0&crop=1&crop=1&height=720&id=oph1H&margin=%5Bobject%20Object%5D&name=image.png&originHeight=720&originWidth=1280&originalType=binary&ratio=1&rotation=0&showTitle=false&size=951906&status=done&style=none&title=&width=1280)<br />**递归算法的时间复杂度分析：子问题总数 x 每个子问题的时间**。<br />子问题总数为递归树节点个数，这个比较难看出来，是 O(n^k)，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为 O(k)。所以总时间复杂度为 O(k * n^k)，指数级别。
```go
package main
// @lc code=start
func coinChange(coins []int, amount int) int {
    var dp func(n int) int
    dp = func(n int) int {
        if n == 0 {
            return 0
        }
        if n < 0 {
            return -1
        }
        // 默认使用1块钱 + 1 表示最大值
        res := amount + 1
        for _, coin := range coins {
            subProblem := dp(n - coin)
            if subProblem == -1 {
                continue
            }
            // 还需要加上本次，所以是 +1
            if res > 1+subProblem {
                res = 1 + subProblem
            }
        }
        if res == amount+1 {
            return -1
        } else {
            return res
        }
    }
    return dp(amount)
}

带备忘录的递归

虽然大大减少了子问题数量，但子问题总数不会超过金额数 n，子问题个数是 n ，处理子问题时间是 DP 学习 - 图9 ，总的时间复杂度是 DP 学习 - 图10


func coinChange(coins []int, amount int) int {
    var dict = make(map[int]int)
    var dp func(n int) int
    dp = func(n int) int {
        if val, ok := dict[n]; ok {
            return val
        }
        if n == 0 {
            return 0
        }
        if n < 0 {
            return -1
        }
        // 默认使用1块钱 + 1 表示最大值
        res := amount + 1
        for _, coin := range coins {
            subProblem := dp(n - coin)
            if subProblem == -1 {
                continue
            }
            // 还需要加上本次，所以是 +1
            if res > 1+subProblem {
                res = 1 + subProblem
            }
        }
        if res == amount+1 {
            return -1
        } else {
            dict[n] = res
            return res
        }
    }
    return dp(amount)
}

DP 数组的迭代解法

换一种自底向上的解题思路

func coinChange(coins []int, amount int) int {
    var dp = make([]int, amount+1)
    dp[0] = 0
    for i := 1; i < len(dp); i++ {
        dp[i] = amount + 1
        for _, coin := range coins {
            if (i - coin) < 0 {
                continue
            }
            if dp[i] > 1+dp[i-coin] {
                dp[i] = 1 + dp[i-coin]
            }
        }
    }
    if dp[amount] == amount+1 {
        return -1
    }
    return dp[amount]
}

总结

计算机解决问题的唯一办法就是穷举。穷举所有可能性。
列出状态转移方程，就是在解决如何穷举的问题。