8. 部分数据结构与算法

数据结构
算法
- 排序算法
增序排序，建大根堆，每次把堆顶元素交换到最后的位置
哈希查找
位图去重

数据结构

栈

特点：后进先出

class Stack:
    def __init__(self):
        self.stack = []
    def push(self, ele):
        self.stack.append(ele)
    def pop(self):
        return self.stack.pop()
    def top(self):
        if not self.stack:
            return 'stack is empty'
        return self.stack[-1]
    def empty(self):
        self.stack = []
    def size(self):
        return len(self.stack)

队列

特点：先进先出

from collections import deque
def use_deque():
    queue = deque(["Eric", "John", "Michael"])
    queue.append('luke')
    queue.appendleft('Alice')
    print(queue)  # deque(['Alice', 'Eric', 'John', 'Michael', 'luke'])
    print(queue.popleft())  # Alice
    print(queue.pop())  # luke
    print(queue)  # deque(['Eric', 'John', 'Michael'])
    queue[0] = 'Bob'
    print(queue)  # deque(['Bob', 'John', 'Michael'])

class CircleQueue:
    def __init__(self, max_size):
        self.max_size = max_size
        self.queue = [0] * max_size
        self.front = 0  # 指向队头元素，初始队头为0
        self.rear = 0  # 指向队尾元素的下一个位置，初始队尾为-1
    def enqueue(self, element):
        if (self.rear + 1) % self.max_size == self.front:
            print('队列满了')
            return False
        self.queue[self.rear] = element
        self.rear = (self.rear + 1) % self.max_size
        return True
    def dequeue(self):
        if self.rear == self.front:
            print('队列为空')
            return False
        element = self.queue[self.front]
        self.front = (self.front + 1) % self.max_size
        return element

二叉树

class Node(object):
    def __init__(self, element=-1, lchild=None, rchild=None):
        self.element = element
        self.lchild = lchild
        self.rchild = rchild
class Tree:
    def __init__(self):
        self.root = None
        self.queue = []
    def build_tree(self, element):
        new_node = Node(element)
        self.queue.append(new_node)
        if self.root is None:
            self.root = new_node  # 树为空，新结点就是树根
        else:
            if self.queue[0].lchild is None:  # 先判断队首结点左边是否为空
                self.queue[0].lchild = new_node
            elif self.queue[0].rchild is None:  # 再判断队首结点右边是否为空
                self.queue[0].rchild = new_node
                self.queue.pop(0)  # 放到右边，两边都放满了，就弹出队首结点
    def pre_order(self, node):
        if node:
            print(node.element, end='')
            self.pre_order(node.lchild)
            self.pre_order(node.rchild)
    def in_order(self, node):
        if node:
            self.in_order(node.lchild)
            print(node.element, end='')
            self.in_order(node.rchild)
    def post_order(self, node):
        if node:
            self.post_order(node.lchild)
            self.post_order(node.rchild)
            print(node.element, end='')
if __name__ == '__main__':
    tree = Tree()
    for i in 'abcdefghij':
        tree.build_tree(i)
    tree.pre_order(tree.root)
    print()
    tree.in_order(tree.root)
    print()
    tree.last_order(tree.root)
    print()

红黑树

基本概念

红黑树是一种自平衡二叉查找树，典型的用途是实现关联数组，在操作系统内核、C++的STL、Java的数据结构中都大量用到红黑树，红黑树的增删查找的复杂度均为logn
红黑树相对于AVL树的时间复杂度是一样的，但是优势是当插入或者删除节点时，红黑树实际的调整次数更少，旋转次数更少，因为红黑树牺牲了部分平衡性以换取插入删除操作时少量的旋转操作，因此红黑树插入删除的效率高于AVL树，大量中间件产品中使用了红黑树
红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色，除了二叉查找树必须满足的一般要求以外，还增加了如下的额外要求
- 性质1：节点是红色或黑色，根是黑色
- 性质2：每个红色节点必须有两个黑色的子节点，可以认为空节点也是黑色节点，所以根到每个叶子节点的路径上都不能有两个连续的红色节点
- 性质3：从任意节点到其每个叶子节点的所有简单路径都包含相同数目的黑色节点
  - 只要从根节点到任意叶子节点的简单路径上的黑色节点数目相等，那么从任意节点到叶子节点的简单路径上的黑色节点数目也是相等的
- 说明：这些约束确保了红黑树的关键特性：从根节点到叶子节点的最长路径不多于最短路径的两倍长。因为根据性质3，从根节点到叶子节点的所有路径上的黑色节点数目相同，根据性质2，最长的路径是黑色节点和红色节点交替，所以得证
说明：在红黑树上进行插入操作和删除操作会导致不再匹配红黑树的性质，恢复红黑树的性质需要少量的颜色变更和不超过三次的树旋转（对于插入操作是两次）

红黑树的插入
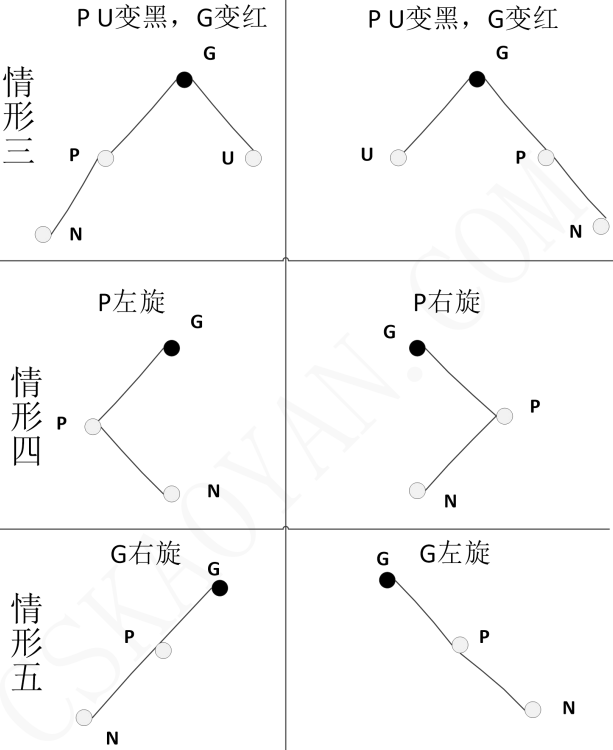
说明：新增节点标为N，颜色为红色；N的父节点标为P，N的祖父节点标为G，N的叔父节点标为U
对于红黑树的插入，可分为以下五种情形
- 情形1：新增节点N位于树根，没有父节点，或者是经过调整后，红黑树的根节点变为红色，此时就将该节点直接标记为黑色
- 情形2：新增节点N的父节点P是黑色，此时无须调整直接插入即可。因为性质2未受影响，新增节点为红色，性质3也未受影响
- 情形3：新增节点N的父节点P和叔父节点U都是红色，此时就将它们俩重绘为黑色，并将祖父节点G重绘为红色。但是，可能会产生以下两种情况
  - 红色的祖父节点G是根节点，此时变为情形1，直接将祖父节点标记为黑色
  - 红色的祖父节点G的父节点也是红色的，此时需要根据G的父亲、爷爷、叔叔的颜色和位置判断是情形3，还是下面的情形4，或者是情形5，符合哪种情形，就按对应情形进行调整即可

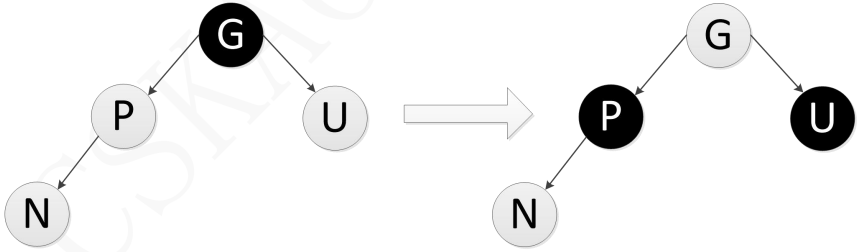
情形4：新增节点N的父节点P是红色而叔父节点U是黑色或者不存在，并且新增节点N是其父节点P的右子节点而父节点P又是其父节点G的左子节点，此时需要对父节点P进行一次左旋转从而调换新增节点N和父节点P的角色，因为节点N和节点P的颜色未改变都是红色，因此仍然不满足性质2，所以需要接着按情形5进行处理以满足性质2

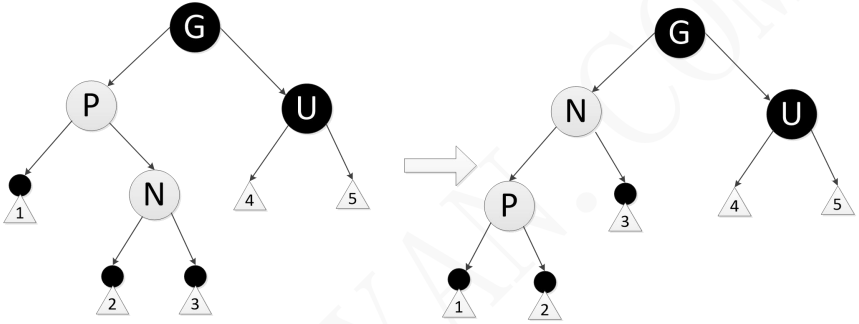
情形5：新增节点N的父节点P是红色而叔父节点U是黑色或者不存在，并且新增节点N是其父节点P的左子节点而父节点P又是其父节点G的左子节点，此时需要对祖父节点G进行一次右旋转。在旋转产生的树中，以前的父节点P现在是新增节点N和以前的祖父节点G的父节点，因为以前的父节点P是红色，所以以前的祖父节点是黑色，所以再交换以前的父节点P和祖父节点G的颜色，使结果的树满足性质3，性质2亦满足

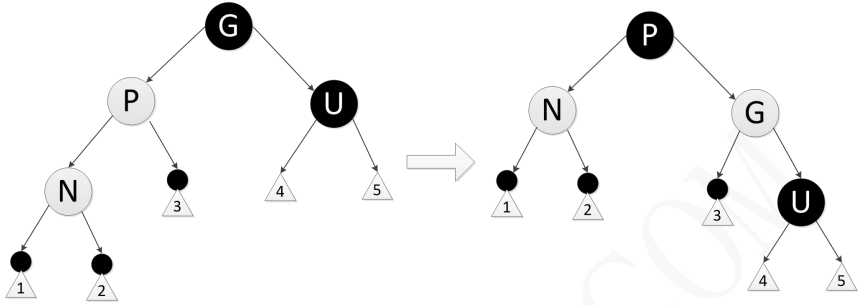
总结

红黑树的删除

待续

算法

排序算法

冒泡排序

方法：假设有n个元素，通过一趟比较，把最大的元素放在最后面，然后将剩余的n - 1个元素再进行一趟比较，再把最大的元素放在最后面，这样进行n - 1趟即可实现数组有序。每一趟比较的策略是相邻两个元素进行比较，如果前一个元素比后一个元素更大，则两两交换，这样交换到最末尾的元素即是这一趟中最大的元素。

def bubule_sort(arr):
    for i in range(len(arr) - 1, 0, -1):  # 每一趟最末尾元素的位置
        for j in range(i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
        print(arr)

选择排序

方法：冒泡排序是把相邻的两个元素进行比较与替换，会造成交换的频率过高。而选择排序是每一趟选出最小元素所在的当前位置，然后将该位置的元素与尚未固定位置的最前面元素进行交换，如此重复n - 1趟，最终数组有序。当然也可以每一趟选出最大元素所在的当前位置，然后将该位置的元素与尚未固定位置的最后面元素进行交换。

#  每一趟选出最小的元素放在最前面
def select_sort(arr):
    for i in range(len(arr) - 1):
        min_pos = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_pos]:
                min_pos = j
        arr[i], arr[min_pos] = arr[min_pos], arr[i]
        print(arr)

插入排序

方法：假设有n个元素，从第2个元素开始进行n - 1趟插入，每一趟从当前元素的上一个位置向前查找到合适位置存放当前元素。向前查找的方法是：如果该位置的元素比当前元素更大，就将其后移一个位置，并继续往前查找；如果该位置的元素小于或等于当前元素，则退出循环，并将当前元素插入到该位置的下一个位置。

def insert_sort(arr):
    for i in range(1, len(arr)):
        insert_value = arr[i]  # 当前元素
        j = i - 1  # 从当前元素的上一个位置开始向前查找合适位置
        while j >= 0:
            if arr[j] > insert_value:
                arr[j + 1] = arr[j]
                j -= 1
            else:
                break
        arr[j + 1] = insert_value
        print(arr)

希尔排序

方法：希尔排序是插入排序的改进版本，又称缩小增量排序，是将间距为step的元素划为一组进行组内插入排序，之后step逐渐缩小直至step为1，完成该趟插入排序后所有的元素即有序。step缩小的策略是：假设有n个元素，第一趟排序的step是n的一半，之后每一趟的step是上一趟step的一半，直至step为1。

def shell_sort(arr):
    step = len(arr) // 2  # 初始步长
    while step > 0:
        for i in range(step, len(arr)):  # 进行一趟希尔排序
            insert_value = arr[i]
            j = i - step
            while j >= 0:
                if arr[j] > insert_value:
                    arr[j + step] = arr[j]
                    j -= step
                else:
                    break
            arr[j + step] = insert_value
        step //= 2
        print(arr)

快速排序

方法：任意选取一个元素作为pivot，然后将比pivot小的元素放在pivot左边，比pivot大的元素放在pivot右边，这样pivot的最终位置确定，然后利用分治的思想将两边的数组继续划分、不断递归，直到最终划分出来的数组只有一个元素，这样整个数组就有序了。

def partition(arr, left, right):
    pivot = arr[left]  # 选取最左边的元素作为pivot
    while left < right:
        while left < right and arr[right] >= pivot:  # 直到arr[right] < pivot，放在pivot左边
            right -= 1
        arr[left] = arr[right]
        while left < right and arr[left] <= pivot:  # 直到arr[left] > pivot，放在pivot右边
            left += 1
        arr[right] = arr[left]
    arr[left] = pivot  # left和right都是pivot的最终位置
    return left
def quick_sort(arr, left, right):
    if left < right:
        pivot_pos = partition(arr, left, right)
        quick_sort(arr, left, pivot_pos - 1)
        quick_sort(arr, pivot_pos + 1, right)

归并排序

方法：多是二路归并排序，核心思想是合并两个有序数组。假设有n个元素，则可将其视为n个有序的子表，每个子表的长度为1，然后两两归并，得到n / 2个长度为2或1的有序表。继续两两归并，直到合并成一个长度为n的有序表为止。

dup_arr = []

def merge(arr, left, mid, right):
    for k in range(left, right + 1):  # 进行数组复制
        dup_arr[k] = arr[k]
    i = left
    j = mid + 1
    k = i
    while i <= mid and j <= right:
        if dup_arr[i] <= dup_arr[j]:  # 选取左边数组的元素
            arr[k] = dup_arr[i]
            i += 1
        else:
            arr[k] = dup_arr[j]  # 选取右边数组的元素
            j += 1
        k += 1
    while i <= mid:  # 左边数组还剩元素，右边数组没剩
        arr[k] = dup_arr[i]
        k += 1
        i += 1
    while j <= right:
        arr[k] = dup_arr[j]  # 右边数组还剩元素，左边数组没剩
        k += 1
        j += 1


def real_merge_sort(arr, left, right):
    if left < right:
        mid = (left + right) // 2
        real_merge_sort(arr, left, mid)
        real_merge_sort(arr, mid + 1, right)
        merge(arr, left, mid, right)


def merge_sort(arr):
    global dup_arr
    dup_arr = [0 for i in range(len(arr))]
    real_merge_sort(arr, 0, len(arr) - 1)

堆排序

堆：n个元素序列L[1…n]称为堆，当且仅当该序列满足：
- 大根堆(大顶堆)：L(i) >= L(2 i) 且 L(i) >= L(2 i + 1)
- 小根堆(小顶堆)：L(i) <= L(2 i) 且 L(i) <= L(2 i + 1)
堆排序需要解决两个问题
- 将无序序列构造成初始堆
- 输出堆顶元素后，将剩余元素调整成新堆
构造初始堆的方法：依次对各节点L(n / 2) ~ L(1)为根的子树进行向下调整，每次调整是直到以该结点为根的子树构成堆为止
调整成新堆的方法：输出堆顶元素后，将堆的最后一个元素与堆顶元素进行交换，然后对堆顶元素进行向下调整 ```python
增序排序，建大根堆，每次把堆顶元素交换到最后的位置
def adjust_max_heap(arr, start_pos, end_pos): dad = start_pos son = 2 * dad + 1 while son <= end_pos:
```
  if son + 1 <= end_pos and arr[son] < arr[son + 1]:
      son += 1
  if arr[son] > arr[dad]:
      arr[son], arr[dad] = arr[dad], arr[son]
      dad = son
      son = 2 * dad + 1
  else:
      break
```

def heap_sort(arr): length = len(arr) for i in range(length // 2 - 1, -1, -1): # 建堆 adjust_max_heap(arr, i, length - 1) arr[0], arr[length - 1] = arr[length - 1], arr[0] for i in range(length - 2, 0, -1): # 调整成新堆 adjust_max_heap(arr, 0, i) arr[0], arr[i] = arr[i], arr[0]

<a name="bs2O2"></a>
#### 计数排序
方法：计数排序是采用空间换时间的方式提高效率，遍历整个数组，统计其中每个元素出现的次数到一个新的数组中，接着依次填入原数组。比如0出现了122次，那么原数组的从下标0到下标121的位置全部填写为0，然后1出现了308次，那么原数组的从下标122到下标429的位置全部填写为1，这样不断进行，最终使原数组有序。
<a name="i3iiJ"></a>
### sorted应用场景
<a name="Zhql3"></a>
#### 简要介绍

- sort函数和sorted函数的区别
   - sort函数仅可以对列表进行排序；而sorted函数可以对任意迭代器进行排序
   - sort函数会影响列表本身，没有返回值；而sorted函数不会改变原有的迭代器，而是返回一个新的排好序的迭代器
- 语法格式
   - sort函数：`list.sort(cmp=None, key=None, reverse=False)`
   - sorted函数：`sorted(iterable, cmp=None, key=None, reverse=False)`
   - 参数说明
      - cmp：可选参数，如果指定了该参数会使用该参数所指定的函数进行排序。该函数具有两个参数，参数的值都是从可迭代对象中取出，此函数**必须遵守**的规则是：大于返回1，小于返回-1，等于返回0
         - 注意：Python3去除了cmp可选参数，如果需要自定义排序规则，需要使用内置的函数将cmp指定的函数转化为key的值
      - key：可选参数，指定用来进行比较的元素，也可以指定函数
      - reverse：排序规则，reverse=True表示降序，reverse=False表示升序（默认）
   - 说明：无论是sort函数还是sorted函数，传入参数key比传入参数cmp的效率更高。因为cmp传入的函数在整个排序过程中会被调用多次，而key针对每个元素仅做一次处理
- 说明：sorted排序是稳定的，即有相同key值的多个记录进行排序之后，原始的前后关系保持不变
<a name="xtUEY"></a>
#### 基本排序
```python
print(sorted([1, 3, 2, 4, 5, 3, 2]))  # [1, 2, 2, 3, 3, 4, 5]
print(sorted({1: 'D', 2: 'B', 4: 'B', 3: 'E', 5: 'A'}))  # [1, 2, 3, 4, 5]
print(sorted("This is a test string from Andrew".split()))  
# ['Andrew', 'This', 'a', 'from', 'is', 'string', 'test']

指定key参数

# 例一：排序列表内是元组
student_tuples = [
    ('Bob', 'B', 12),
    ('Alan', 'B', 10),
    ('John', 'A', 15),
]

def get_name(student):
    return student[0]

print(sorted(student_tuples, key=get_name))
# [('Alan', 'B', 10), ('Bob', 'B', 12), ('John', 'A', 15)]
print(sorted(student_tuples, key=lambda s: s[1]))
# [('John', 'A', 15), ('Bob', 'B', 12), ('Alan', 'B', 10)]


# 例二：排序列表内是自定义对象
class Student:
    def __init__(self, name, grade, age):
        self.name = name
        self.grade = grade
        self.age = age

    def __repr__(self):
        # str返回的必须是字符串类型，repr和str功能一样，只是可以返回不是字符串的类型
        return repr([self.name, self.grade, self.age])

print(Student('john', 'A', 15))  # ['john', 'A', 15]

student_lists = [
    Student('Bob', 'B', 12),
    Student('Alan', 'B', 10),
    Student('John', 'A', 15),
]
print(sorted(student_lists, key=lambda s: s.name))
# [['Alan', 'B', 10], ['Bob', 'B', 12], ['John', 'A', 15]]


# 例三：一种特殊用法
print(sorted("This is a test string from Andrew".split(), key=str.lower))
['a', 'Andrew', 'from', 'is', 'string', 'test', 'This']


# 例四：对多字段排序
list1 = [[1, 3], [4, 1], [4, 2], [3, 0], [5, 2], [3, 3]]
print(sorted(list1, key=lambda s: (s[0], s[1])))
# [[1, 3], [3, 0], [3, 3], [4, 1], [4, 2], [5, 2]]
print(sorted(list1, key=lambda s: (s[0], -s[1])))
# [[1, 3], [3, 3], [3, 0], [4, 2], [4, 1], [5, 2]]

混合字典的排序

# 列表中混合字典
game_result = [
    {"name": "Bob", "wins": 10, "losses": 3, "rating": 75.00},
    {"name": "David", "wins": 3, "losses": 5, "rating": 57.00},
    {"name": "Carol", "wins": 4, "losses": 5, "rating": 57.00},
    {"name": "Patty", "wins": 9, "losses": 3, "rating": 71.48}]

print(sorted(game_result, key=lambda s: (s["rating"], s["name"])))


# 字典中混合列表
dict1 = {'Li': ['M', 7],
         'Zhang': ['E', 2],
         'Wang': ['P', 3],
         'Du': ['C', 2],
         'Ma': ['C', 9],
         'Zhe': ['H', 7]}

print(sorted(dict1.items(), key=lambda v: v[1][1]))
'''
[('Zhang', ['E', 2]), ('Du', ['C', 2]), ('Wang', ['P', 3]), 
('Li', ['M', 7]), ('Zhe', ['H', 7]), ('Ma', ['C', 9])]
'''

print(dict(sorted(dict1.items(), key=lambda v: v[1][1])))
'''
{'Zhang': ['E', 2], 'Du': ['C', 2], 'Wang': ['P', 3], 
'Li': ['M', 7], 'Zhe': ['H', 7], 'Ma': ['C', 9]}
'''

使用库函数

student_tuples = [
    ('Bob', 'B', 12),
    ('Alan', 'B', 10),
    ('John', 'A', 15),
]

student_lists = [
    Student('Bob', 'B', 12),  # Student类如上
    Student('Alan', 'B', 10),
    Student('John', 'A', 15),
]

from operator import itemgetter, attrgetter

print(sorted(student_tuples, key=itemgetter(1, 2)))
# [('John', 'A', 15), ('Alan', 'B', 10), ('Bob', 'B', 12)]
print(sorted(student_lists, key=attrgetter('grade', 'age'), reverse=True))
# [['Bob', 'B', 12], ['Alan', 'B', 10], ['John', 'A', 15]]

自定义排序规则

由于python3中的sorted函数去除了cmp参数，无法自定义排序规则，因此需要使用内置的函数将cmp函数转化为key的值
说明
- 使用functools.cmp_to_key()将cmp函数转化为key
- cmp函数的返回值必须是[1, -1, 0]
例题：给定一个正整数数组，求把数组里面的所有数拼接起来的数字中的最大值 ```python from functools import cmp_to_key

def compare(str1, str2): if str1 + str2 < str2 + str1: return 1 elif str1 + str2 > str2 + str1: return -1 else: return 0

def solution(arr): str_list = [str(i) for i in arr] sorted_str_list = sorted(str_list, key=cmp_to_key(compare)) return ‘’.join(sorted_str_list)

if name == ‘main‘: list1 = [3, 32, 321, 3] print(solution(list1)) # 3332321

<a name="L4Qqp"></a>
### 二分查找
注意：查找数组要保证有序
```python
def binary_search(arr, target):
    right = len(arr) - 1
    left = 0
    while left <= right:  # 注意：这里一定要取等号
        mid = (left + right)
        if arr[mid] > target:
            right = mid - 1
        elif arr[mid] < target:
            left = mid + 1
        else:
            return mid
    return -1

哈希查找

哈希又叫散列，哈希表是根据键直接访问内存存储位置的数据结构，哈希查找通过关于键值的映射函数，将所需查询的数据映射到表中的一个位置来访问记录，从而加快了查找速度。

def elf_hash(hash_str):
    h = 0
    g = 0
    for i in hash_str:
        h = (h << 4) + ord(i)
        g = h & 0xf0000000
        if g:
            h ^= g >> 24
        h &= ~g
    return h % MAXKEY

str_list = ["xiongda", "lele", "hanmeimei", "wangdao", "fenghua"]
hash_table = [None] * MAXKEY
for i in str_list:
    hash_table[elf_hash(i)] = i

位图去重

用某一位来标记对应数是否出现过，如果该位为0，就表示对应数没出现过；如果该位为1，就表示对应数出现过

def bitmap(arr):
    int_bitmap = 0
    result = []
    for i in arr:
        if not int_bitmap & 1 << i:
            result.append(i)
            int_bitmap |= 1 << i  # 这个数出现了，就把对应位置标记为1
    return result