1.数组

1.栈

1.有效的括号-20

指定一个由{}、[]、()三种组成的括号字符串，来校验是否是有效匹配的字符串。

  1. /**
  2.     思路：
  3.         1、初始校验、判断是否为空、是否为奇数（这两种情况直接返回结束）
  4.         2、转换为字节数组、将对立的另一半压入栈中；
  5.         3、遍历压入另一半元素时，如果元素不相等、或者栈为空则认为不匹配
  6. */
  7. public class Solution{
  8.     public boolean solution(String str){
  9.         // 初始校验
  10.         if(str.isEmpty()){
  11.             return false;
  12.         }
  14.         // 转换为字符数组、循环压入另一半入栈
  15.         Stack<Character> stack = new Stack<Character>();
  16.         for(char s : str.toCharArray()){
  17.             if(s == '('){
  18.                 stack.push(')');
  19.             }else if(s == '['){
  20.                 stack.push(']');
  21.             }else if(s == '{'){
  22.                 stack.push('}');
  23.             }else if(stack.isEmpty() || s != stack.pop()){
  24.                 // 为空，则表示为奇数个、不相等则表示不匹配
  25.                 return false;
  26.             }
  27.             return stack.isEmpty();
  28.         }
  29.     }
  30. }

2.链表

1.环形链表

给定一个链表、其中pos指示的是表尾部指向形成环状结点的位置，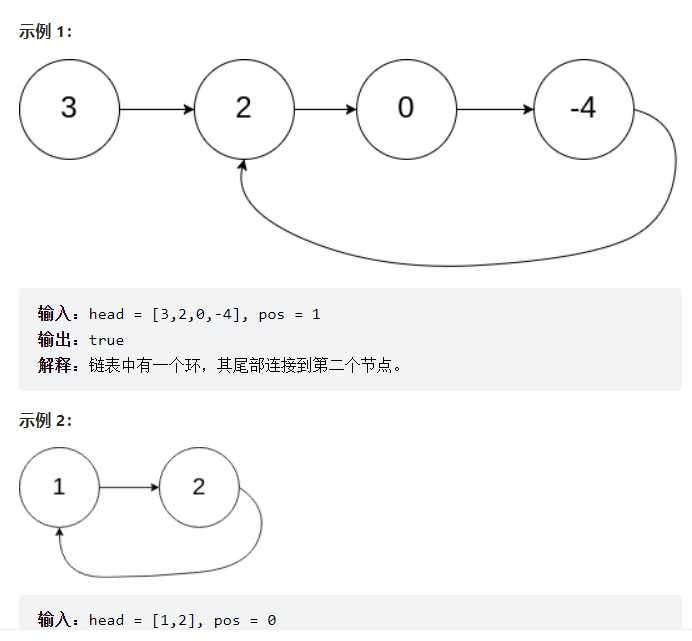
image.png

  1. /**
  2.     思路：
  3.         定义双指针、初始均为指向头结点
  4.         1、preNode指针每次移动两个元素
  5.         2、currNode指针每次移动一个元素
  6.         3、当两个指针相等时，则会追上，表示存在环形链表
  7. */
  8. public class Solution{
  9.     public boolean solution(ListNode head){
  10.         ListNode preNode, currNode = head;
  12.         while(preNode != null && preNode.next != null){
  13.             preNode = preNode.next.next;
  14.             currNote = currNode.next;
  15.             if(currNode == preNode) return true;
  16.         }
  18.         return false;
  19.     }
  20. }

2.反转链表

给定一个链表，返回反转后的链表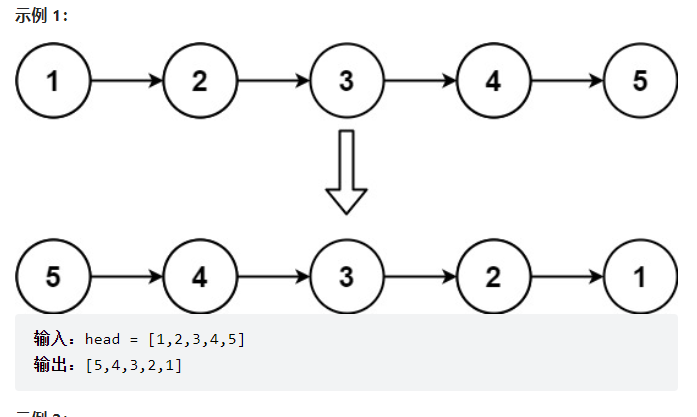
image.png

  1. public class Solution{
  2.     public ListNode reverserNode(ListNode head){
  3.         // 定义当前指针指向头结点
  4.         ListNode curr = head;
  5.         // 定义前指针、临时指针
  6.         ListNode pre, temp = null;
  7.         while(curr != null){
  8.             // 将临时指针指向第一个结点的下一个结点
  9.             temp = curr.next;
  10.             // 将当前结点的next指向pre
  11.             curr.next = pre;
  12.             // 分别移动pre、curr
  13.             pre = curr;
  14.             curr = temp;
  15.         }
  16.         return pre;
  17.     }
  18. }

2.Map容器

1.两数相加

给定一个不重复元素的数组、指定一个目标值、求出数组中 num1 + num2 = target元素的下标数组

  1. /**
  2.     思路：
  3.         1、利用Map键值对的特性、存储元素值key、对应的索引下标i
  4.         2、循环遍历数组，target - nums[0]后的值加入Map中；
  5.         3、遍历第二个元素，当target -nums[1]后的值等于第一次加入Map中元素的值，则返回数组
  6.         4、如果仍然不相等，则再次加入当前值。
  7. */
  8. public class Solution{
  9.     public int[] twoSum(int[] nums, int target){
  10.         // Map存储元素
  11.         HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
  12.         for(int i = 0; i < nums.lenght; i++){
  13.             if(map.containsKey(target - nums[i])){
  14.                 // target - 当前值后的元素存在之前加入的map容器中
  15.                 return new int[]{map.get(target - nums[i]), i};
  16.             }
  17.             // 不存在，则加入当前元素
  18.             map.put(nums[i], i);
  19.         }
  20.         // 未找到则返回空
  21.         return null;
  22.     }
  23. }

2.只出现一次的数字

给定一个整数数组、只包含一个出现一次的数字、其余都是两次、找出出现一次的数字

  1. /**
  2.     思路：使用hash表
  3.         存在，则value+1，不存在，则value=1
  4. */
  5. public class Solution{
  6.     public int singletonValue(int[] nums){
  7.         Map<Integer, Integer> map = new HashMap<>();
  9.         // 遍历元素放入hash表中
  10.         for(Integer i : nums){
  11.             Integer count = map.get(i);
  12.             count = count == null ? 1 : ++count;
  13.             map.put(i. count);
  14.         }
  16.         // 找出value为1的值
  17.         for(Integer i : map.keySet()){
  18.             if(map.get(i) == 1){
  19.                 return i;
  20.             }
  21.         }
  23.         return -1;
  24.     }
  25. }

3.滑动窗口-不重复的最长字符串长度

image.png

  1. /**
  2.     思路：
  3.         1、使用Map容器记录遍历后的元素、key=元素值-value=索引值
  4.         2、当出现重复元素时、则改变起始不重复元素的索引指针
  5.         3、通过right - left + 1计算最大长度
  6. */
  7. public class Solution{
  8.     public int maxLength(String s){
  9.         // 获取长度
  10.         int length = s.length();
  12.         if(length == 0){
  13.             return 0;
  14.         }
  15.         // Hash结构，存储元素
  16.         HashMap<Character, Integer> map = new HashMap<>();
  18.         // 循环遍历元素
  19.         int max = 0;
  20.         int left = 0;
  21.         for(int i = 0; i < length; i++){
  22.             if(map.containsKey(s.charAt(i))){
  23.                 // 包含重复元素。则改变起始位置
  24.                 left = Math.max(left, map.get(s.charAt(i)) + 1);
  25.             }
  26.             // 不重复则加入元素
  27.             map.put(s.charAt(i), i);
  28.             // 计算最大长度
  29.             max = Math.max(max, i - left + 1);
  30.         }
  31.         return max;
  32.     }
  33. }

3.递归

1.合并两个有序链表-21

指定两个递增的有序链表、将其从小到大进行合并，返回合并后的递增有序链表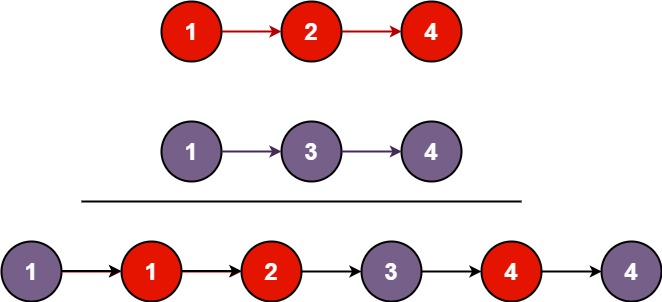
数据结构与算法 - 图4

  1. /**
  2.     思路：
  3.         1、递归思路求解
  4.         2、第一次比较、list1中的1与list2中的2比较、
  5.                 如果list1中的1结点 < 小于list2中的1结点，则比较list1中的2结点与list2中所有结
  6.                 点。大于，则相反思想
  7.         3、当list1、list2中有一个为空则进行返回
  8. */
  10. /**
  11.  * Definition for singly-linked list.
  12.  * public class ListNode {
  13.  *     int val;
  14.  *     ListNode next;
  15.  *     ListNode() {}
  16.  *     ListNode(int val) { this.val = val; }
  17.  *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
  18.  * }
  19.  */
  20. public class Solution{
  21.     public ListNode mergeListNode(ListNode list1, ListNode list2){
  22.         if(list1 == null){
  23.             return list2;
  24.         }
  25.         if(list2 == null){
  26.             return list1;
  27.         }
  29.         // 递归调用合并
  30.         if(list1.val < list2.val){
  31.             // 递归比较list1的下一个结点与list2中的所有结点
  32.             list1.next = mergeListNode(list1.next, list2);
  33.             return list1;
  34.         }else{
  35.             // 反过来进行递归
  36.             list2.next = mergeListNode(list2.next, list1);
  37.             return list2;
  38.         }
  39.     }
  40. }

4.动态规划

1.最大子数组和

给定一个数组、求出最大值连续子数组，返回最大值
image.png

  1. /**
  2.     思路：
  3.         关键词：连续、最大和、具有最大和的连续子数组
  4.         动态规划：大问题化为若干子问题，求最优解
  5.     1、如何划分子问题
  6.         第一种：我们无法确定最大和连续子数组中到底包含哪一个，但是可以知道经过每一个元素的最大和，然后在所有的最大和数组中找出最大值即可（最优解）
  7.             1.子问题1：经过-2的连续子数组最大和？
  8.             2.子问题2：经过1的连续子数组最大和？
  9.               ......
  10.             9.子问题9：经过4的连续子数组最大和？
  11.         第二种：上述分析中，每个子问题中又包含不确定性，无法确定子问题中到底有多少中情况。因此、我们还要进行其他方式划分
  12.             1.子问题1：以-2结尾的连续子数组最大和？
  13.             2.子问题2：以1结尾的连续子数组最大和？
  14.                 ......
  15.             9.子问题9：以4结尾的连续子数组最大和？
  16.      2、如何确定状态转换
  17.          上述问题中，可能存在两种类型、全部大于0，与不全部大于0。这两种状态中，以nums[i]结尾的元素一定会被包含到，则只需要考虑剩余nums[i - 1]的状态。
  18.          1、如果全部或部分 > 0（且dp[i - 1] > 0），则dp[i] = dp[i - 1] + nums[s];
  19.          2、如果剩余部分 <= 0（且dp[i - 1] <= 0），则dp[i] = nums[i]
  20.          故状态转义方程如下：
  21.                          dp[i - 1] + nums[i],        dp[i - 1] > 0
  22.              dp[i] = {
  23.                          nums[i],                    dp[i - 1] <= 0
  24. */
  25. public class Solution{
  26.     public int maxSubArray(int[] nums){
  27.         // 定义状态数组
  28.         int len = nums.length;
  29.         int[] dp = new int[len];
  31.         // 初始化初值
  32.         dp[0] = nums[0];
  34.         // 根据状态转移方程计算子问题
  35.         for(int i = 1; i < len; i++){
  36.             if(dp[i - 1] > 0){
  37.                 // dp[i - 1] > 0，直接相加
  38.                 dp[i] = dp[i - 1] + nums[i];
  39.             }else{
  40.                 // dp[i - 1] <= 0
  41.                 dp[i] = nums[i];
  42.             }
  43.         }
  45.         // 从dp数组中寻找最大值
  46.         int result = dp[0];
  47.         for(int i = 1; i < len; i++){
  48.             result = Math.max(result, dp[i]);
  49.         }
  50.         return result;
  51.     }
  52. }

2.爬楼梯

假设存在n阶楼梯、每次只能爬1或2个台阶。求出有多少中走法；

  1. /**
  2.     思路：
  3.         关键词：共n阶、每次只能爬1或2阶。求走法？
  4.         动态规划，划分子问题、求子问题中的最优解
  5.     1、划分子问题
  6.         1.总共n阶楼梯
  7.         2.第n阶只有一种走法、则第n-1阶有多少种走法、第n-2阶有多少种走法
  8.     2、定义状态方程
  9.         0    1    2    3    5        走法
  10.         0    1    2    3    4        阶数
  11.         规律：从2开始，每一阶走法都是n-1 + n-2阶之和
  13.         dp[n] = dp[n - 1] + dp[n - 2]
  14. */
  15. class Solution {
  16.     public int climbStairs(int n) {
  17.         if(n <= 2){
  18.             return n;
  19.         }
  20.         // 定义状态数组
  21.         int[] dp = new int[n + 1];
  23.         // 初始化初值
  24.         dp[0] = 0;
  25.         dp[1] = 1;
  26.         dp[2] = 2;
  28.         // 循环处理3阶以上问题
  29.         for(int i = 3; i <= n; i++){
  30.             dp[i] = dp[i - 1] + dp[i - 2];
  31.         }
  32.         return dp[n];
  33.     }
  34. }

3.买卖股票最佳时机

给定一个股票数组、只能单次的买卖、当前买入、在未来的某一天卖出股票、求最大利润。
注意：不能在买入前进行卖出、不能在同一天进行买卖
image.png

  1. /**
  2.     思路：动态规划
  3.         1、状态划分：
  4.             dp[i][0]：表示在[0 - i]区间范围内，第i天结束之后不持有股票
  5.                       此时利润为0
  6.             dp[i][1]：表示在[0 - i]区间范围内，第i天结束之后持有股票
  7.                       此时利润为第i天的负数 -precies[i]
  8.         2、状态转义方程
  9.              第一天：
  10.                  dp[0][0]：不持股、则最大利润为0
  11.                  dp[0][1]：持股、则最大利润为这一天的负数-prices[i]
  12.              第二天：
  13.                  dp[1][0]：未持股、或者持股卖出（两者中间取最大值）
  14.                              则最大利润为dp[i - 1][0], dp[i - 1][i] + prices[i];
  15.                  dp[1][1]：持股则和之前的进行比较、取一个较大值
  16.                              则最大利润为dp[i - 1][1], -prices[i]
  17. */
  18. public class Solution{
  19.     public int maxPrice(int[] prices){
  20.         // 排除基本情况
  21.         int len = prices.length;
  22.         if(len < 2){
  23.             return 0;
  24.         }
  26.         // 定义状态方程
  27.         int[][] dp = new dp[lne][2];
  29.         // 初始化第一天的值
  30.         dp[0][0] = 0;
  31.         dp[0][1] = -prices[0];
  33.         // 从第二天开始进行遍历
  34.         for(int i = 1; i < len; i++){
  35.             // 不持股、或者持股卖出
  36.             dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
  37.             dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
  38.         }
  40.         // 返回最后一次最大值即可
  41.         return dp[len - 1][0];
  42.     }
  43. }

4.最长回文子串

给定一个字符串、找出最长的回文字符串
image.png

  1. /**
  2.     思路：动态规划求解最优解（最大值）
  3.         1、定义状态方程组
  4.             初始化一个二维数组、用来记录动态规划中的变化值
  5.         2、初始化化方程组
  6.             对角线元素中的自身都是回文字符串、可以初始化为true
  7.         3、状态转义方程
  8.             1、从第一个字符开始、逐渐扩宽字符区间、然后在从每个字符区间进行缩小
  9.             2、外层循环控制扩宽区间、内层循环控制缩减每个区间
  10.                         false,                chars[i] != chars[j]
  11.             dp[i][j] = 
  12.                         j-i < 3||dp[i+1][j-1]
  13. */
  14. public class Solution{
  15.     public String maxString(String s){
  16.         // 获取字符串长度
  17.         int len = s.length();
  19.         if(len == 1){
  20.             return s;
  21.         }
  23.         // 定义状态方程
  24.         boolean[][] dp = new boolean[len][len];
  25.         // 获取字符数组
  26.         char[] chars = s.toCharArray();
  28.         // 初始化初始值
  29.         for(int i = 0; i < len; i++){
  30.             dp[i][i] = true;
  31.         }
  33.         // 定义最大长度、开始位置
  34.         int maxLen = 1;
  35.         int begin = 0;
  36.         // 循环开始遍历元素
  37.         for(int j = 1; j < len; j++){
  38.             for(int i = 0; i < j; i++){
  39.                 // 判断当前区间中的两端是否相同
  40.                 if(chars[i] != chars[j]){
  41.                     dp[i][j] = false;
  42.                 }else{
  43.                     // 相同，则判断剩余个数是否小于3
  44.                     if(j - i < 3){
  45.                         dp[i][j] = true;
  46.                     }else{
  47.                         dp[i][j] = dp[i + 1][j - 1];
  48.                     }
  49.                 }
  50.             }
  52.             // 改变长度、开始位置
  53.             if(dp[i][j] && j - i + 1 > maxLen){
  54.                 maxLen = j - i + 1;
  55.                 begin = i;
  56.             }
  57.         }
  59.         // 返回最大回文子串
  60.         return s.substring(begin, begin + maxLen);
  61.     }
  62. }