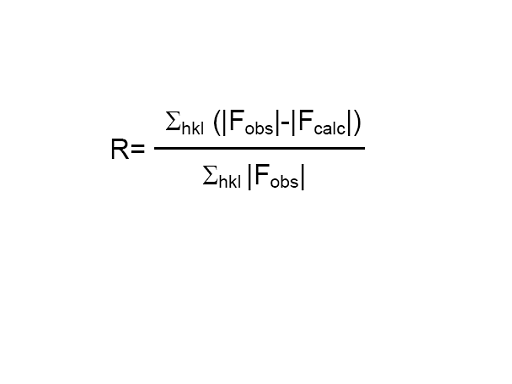PDB知识

R factor

评估pdb结构的准确性的，越小越好，但越小也不代表越正确 参考

藉由电子密度图的三维构形，可将每一个胺基酸依蛋白质序列建立蛋白质的起始模型。蛋白质的起始模型，常由于相角的解不够完美，使计算出来的电子密度图产生误差，误导模型的走向，因此需要做进一步的改善，称为修正(refinement)。修正的目的在于进行立体化学(stereochemistry)(如胜 键键长、键角、胺基酸构形)优化的同时，减少计算与实验绕射点强度的差异，用来评估的数值则是「剩余值(R-factor)」：
其中Fobs 及Fcalc 分别表示观察值与计算值的绕射光振幅。尽可能将剩余值降到最低，直到进一步的修正无法减少其值为止，即达最终的蛋白质结构模型。大部分修正后可接受的剩余值约0.2 (20%)。但低的剩余值，并不代表其结构就是正确的。

RMSD

昨天，和朋友一起讨论同源建模的问题。他告诉我说，建模的结果于模板之间的RMSD是0.347….当时就觉得有点奇怪，他是怎么计算这个数值的。所以这里一起讨论下RMSD

先看看RMSD的计算公式（转自http://en.wikipedia.org/wiki/Root_mean_square_deviation_(bioinformatics)）
RMSD(Root Mean Squared Deviation)

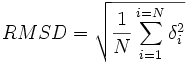
where δ is the distance between N pairs of equivalent atoms (usually Cα and sometimes C,N,O,Cβ). Normally a rigid superposition which minimizes the RMSD is performed, and this minimum is returned. Given two sets of n points and , the RMSD is defined as follows:

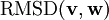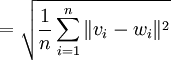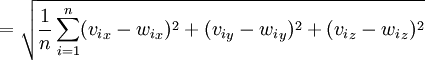An RMSD value is expressed in length units. The most commonly used unit in structural biology is the Ångström (Å) which is equal to 10–10m.

—-> 用来表是蛋白质结构之间差异的参数是两个结构之间原子位置的 RMSD。

—-> 计算RMSD时，可以针对目标蛋白质(如: 所有的原子、骨干部份或只考虑 alpha 碳原子等等)。不同的标准，计算RMSD的数值会有所差异。

—-> RMSD 距离函数，以一个结构中的原子与另外一个结构中对应原子为计算标的，因此，如果两个分子在座标系统中以不同的位置开始计算，那么不管其结构是否相似，这两者之间的 RMSD 必定相当大。也因为这样，我们为了要计算有意义的 RMSD ，两者的结构要尽可能的重叠。
对于docking而言，如果有reference ligand，一般不需要额外的重叠，否则会有伪造数据之嫌。

—-> 可以通过计算 RMSD 来当作评估蛋白质结构的可信度: 在模拟过程中，分子会不断的发生变化，而对于我们而言，必须等到分子结构在稳定的状态下(fluctuation较小时)再进一步进行分析，这样才比较有意义。

对于序列和长度不同的蛋白结构，比较RMSD似乎意义不大。
对于存在序列和长度差异的蛋白，首先我们不知道软件本身在计算RMSD的时候究竟采用了何种计算方法：所有原子？骨架部分？还是CA？这样就很难给我们一个明确的概念。
另外，对于长短不一的蛋白，软件首先会对序列进行比较，本身比对的方法不同，显然会给后面的结果带来影响。
另外，对于长短不一的蛋白，软件究竟取多少残基作为计算RMSD的对象，我们也无从知道。

所以，对于不是同一个蛋白的RMSD的计算，其中的不确定性比较多，计算出来的结果只能作为参考，给我们一个大概的概念。