如何绘制一个美观且便于理解的有向无环图？本文以d3-dag实现为例，浅析Sugiyama层次布局算法

前言

如何绘制一个美观且便于理解的有向无环图（DAG）？
对于有一定依赖关系的DAG而言，以下几个要点被广泛用于布局中。

  • 布局均衡，节点均匀分布
  • 边以直线为主
  • 减少长边
  • 减少边交叉

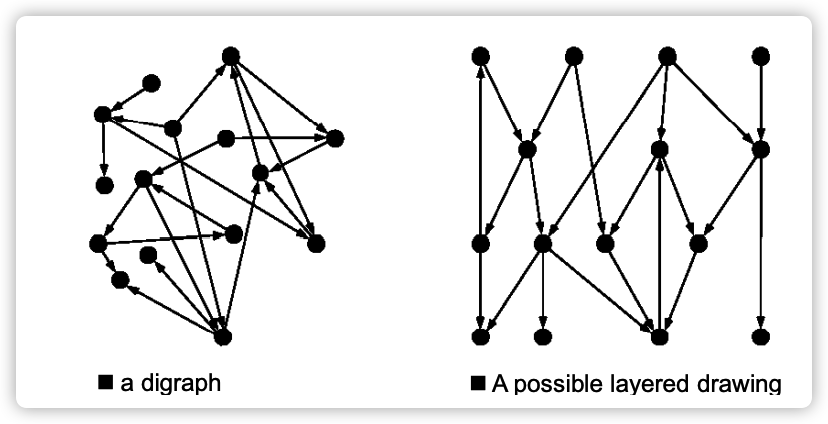
image.png

Sugiyama布局

基于以上的目标， Kozo Sugiyama 在1981年提出有层级结构关系的图布局算法，因此又被称为Sugiyama方法。

该布局方法主要分为以下三个步骤，每个步骤都可以有多种不同实现方式：

1. 节点分层 - Layering

根据边的方向将每个节点划分到不同层（rank），通过增加伪节点（dummy node）使得每条边仅连接相邻两层，每多一个伪节点意味着多一个可能导致边弯曲的点。

例如节点A在第1层，节点B在第3层同时有边 A->B，那么在第2层额外添加节点C，并修改边为 A->C->B

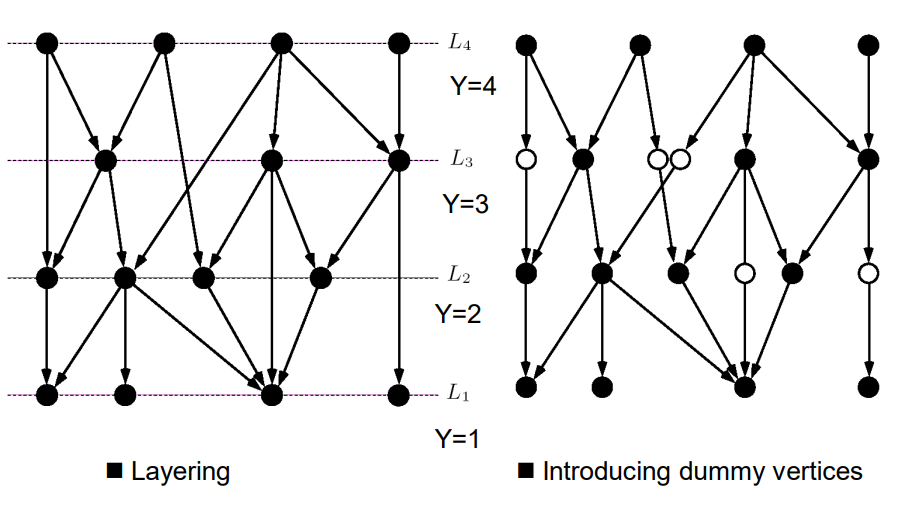
image.png

2. 减少边交叉 - Decorssing

这个步骤又叫做节点重排序，因为唯一影响边交叉的就是节点的次序，所以该步骤通过重新计算节点在当前层级的次序来减少边的交叉，通常是最耗时的一步。
image.png

3. 计算坐标 - Coordinate assignment

基于上面计算得到的层级和次序来计算真实节点的横坐标和纵坐标，尽量减少去除伪节点后边弯曲的程度，同时布局尽可能平衡。
一般而言，节点的纵坐标可以直接基于层级和层高，因此该步骤的实现侧重于计算横坐标。

d3-dag中的实现

d3-dag是一个用于DAG操作和布局的d3插件库，内置了Sugiyama布局的一些简单实现。d3-dag将Sugiyama布局的三个步骤拆分为三个算子，分别是LayeringOperator，DecrossOperator和CoordOperator。

0. 数据结构

DagLink - 边

DAG中的边

  1. interface DagLink<NodeDatum = unknown, LinkDatum = unknown> {
  2.   readonly source: DagNode<NodeDatum, LinkDatum>;
  3.   readonly target: DagNode<NodeDatum, LinkDatum>;
  4.   readonly data: LinkDatum;
  5.   readonly points: { readonly x: number; readonly y: number }[];
  6. }

DagNode - 节点

DAG中的节点

  1. interface DagNode<NodeDatum = unknown, LinkDatum = unknown>
  2.   extends Dag<NodeDatum, LinkDatum> {
  3.   readonly data: NodeDatum;
  4.   value?: number;
  5.   x?: number;
  6.   y?: number;
  7.   children(): DagNode<NodeDatum, LinkDatum>[];
  8.   childLinks(): DagLink<NodeDatum, LinkDatum>[];
  9. }

Dag - 图

其中count() height() depth() 都是给每个节点初始化层级value。

  • count：每个节点下面的叶子数，叶子节点为1。
  • height：每个节点离叶子的最长距离，叶子节点为0。
  • depth：每个节点离根节点的最长距离，根节点为0。
  1. export type IterStyle = "depth" | "breadth" | "before" | "after";
  3. interface Dag<NodeDatum = unknown, LinkDatum = unknown>
  4.   extends Iterable<DagNode<NodeDatum, LinkDatum>> {
  5.   roots(): DagNode<NodeDatum, LinkDatum>[];
  6.   /** 后代节点 */
  7.   descendants(style?: IterStyle): DagNode<NodeDatum, LinkDatum>[];
  8.     /** 所有边 */
  9.   links(): DagLink<NodeDatum, LinkDatum>[];
  10.   size(): number;
  11.   /** 计算节点和 */
  12.   sum(
  13.     callback: (node: DagNode<NodeDatum, LinkDatum>, index: number) => number
  14.   ): this;
  15.   count(): this;
  16.   height(): this;
  17.   depth(): this;
  18.   /** 从根节点拆分DAG为多个连通的DAG */
  19.   split(): Dag<NodeDatum, LinkDatum>[];
  20.   /** DAG是否连通 */
  21.   connected(): boolean;

以下实现都假设输入已经为有向无环图

1. 节点分层

  • 在d3-dag中，如果存在边 A -> B，则A的层级小于B的层级
  • value为节点的层级

a. Longest Path - 最小化高度

其中一个简单实现就是节点的层级等于它的深度（到达它的最长路径）。

  1.   function longestPathCall(dag: Dag): void {
  2.     if (options.topDown) {
  3.       // 自上而下，最长路径将从顶部开始，将节点尽可能靠近顶部
  4.       dag.depth(); // 为每个节点分配层级，等于其距离根节点的最长距离(深度)。
  5.     } else {
  6.       // 自下而上
  7.       dag.height(); // 为每个节点分配层级，等于其距离叶子点的最长距离(高度)。
  8.       // 根节点的最高高度
  9.       const maxHeight = Math.max(...map(dag.iroots(), (d) => d.value));
  10.       for (const node of dag) {
  11.         node.value = maxHeight - node.value;
  12.       }
  13.     }
  14.   }

最长路径算法实现起来比较简单，处理速度非常快。但可能分层的结果会非常宽，节点容易挤到某一边，造成大量留白，效果一般。
image.pngimage.png

b. Coffman Graham - 限制宽度

Coffman Graham 算法最早是用于解决多核CPU任务调度（任务和任务的依赖也可以视作DAG），后来也被用于DAG绘制中的节点分层。其核心在于以下两个限制：

  1. 每层数量/宽度不超过浅析有向无环图DAG的Sugiyama层次布局 - 图6。
  2. 当前层节点的所有依赖必须在当前层上面。

image.png
该算法保证生成的DAG高度h满足 浅析有向无环图DAG的Sugiyama层次布局 - 图8， 其中浅析有向无环图DAG的Sugiyama层次布局 - 图9为指定宽度浅析有向无环图DAG的Sugiyama层次布局 - 图10下分层的最小高度。

  1. function coffmanGrahamCall(dag: Dag): void {
  2.     const maxWidth = options.width || Math.floor(Math.sqrt(dag.size() + 0.5));
  4.     // 创建优先队列，下一个节点为最近完成父节点次序最小的（最大化父子节点分配的次序差）
  5.     function comp(left: DagNode, right: DagNode): boolean {
  6.       const leftBefore = data.get(left).before;
  7.       const rightBefore = data.get(right).before;
  8.       for (const [i, leftb] of leftBefore.entries()) {
  9.         const rightb = rightBefore[i];
  10.         // leftb: left的父节点中最近分配的次序
  11.         // rightb: right的父节点中最近分配的次序
  12.         if (rightb === undefined) {
  13.           return false;
  14.         } else if (leftb < rightb) {
  15.           return true;
  16.         } else if (rightb < leftb) {
  17.           return false;
  18.         }
  19.       }
  20.       return true;
  21.     }
  23.     const queue = new FastPriorityQueue(comp);
  25.     // 从根节点开始
  26.     for (const root of dag.iroots()) {
  27.       queue.add(root);
  28.     }
  29.     let i = 0; // 分配的顺序
  30.     let layer = 0; // 当前分配的层级，从0开始，层级高的在下面
  31.     let width = 0; // 当前层宽度
  32.     let node;
  33.     while ((node = queue.poll())) {
  34.       if (
  35.         width < maxWidth &&
  36.         data.get(node).parents.every((p) => p.value < layer)
  37.       ) {
  38.         // 当前层宽度 < 限宽 且 节点的所有父节点层级比当前层级低
  39.         // 添加节点到当前层
  40.         node.value = layer; 
  41.         width++;
  42.       } else {
  43.         // 否则添加到新的下一层
  44.         node.value = ++layer;
  45.         width = 1;
  46.       }
  47.       for (const child of node.ichildren()) {
  48.         // 对于节点的每个直接子节点（有边），记录已经分配层级的父节点序号
  49.         const { before, parents } = data.get(child);
  50.         before.push(i);
  51.         // 当所有父节点已经分配层级后加入优先队列（拓扑序）
  52.         if (before.length === parents.length) {
  53.           before.sort((a, b) => b - a); // 从大到小排序，最近分配的在前
  54.           queue.add(child);
  55.         }
  56.       }
  57.       i++;
  58.     }
  59.   }

image.png

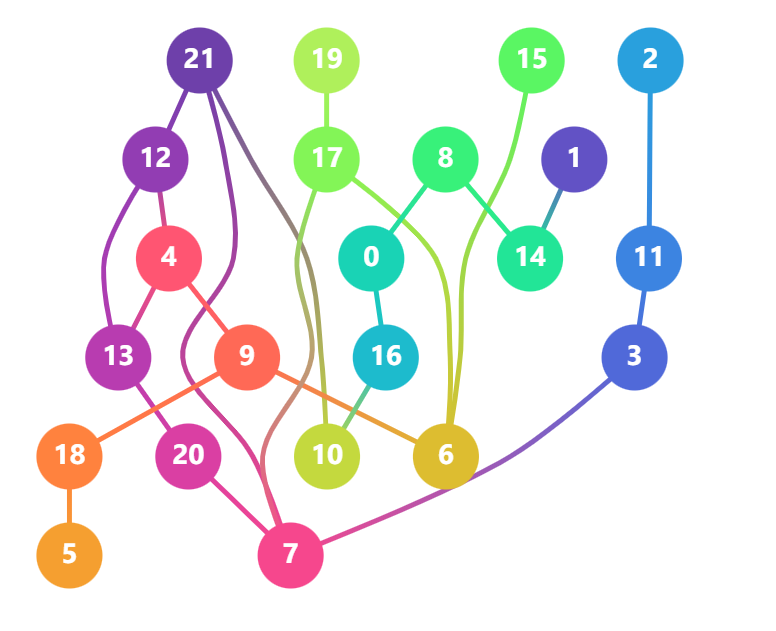
c. Simplex - 最小化边长

该方法通过最小化伪节点的数量来给节点分层，具体实现上和著名的网络单纯型法（network simplex algorithm）类似，因此又被称为Simplex Layering。

因为层级必须是整数，所以也是一个纯整数线性规划问题，最小化总边长浅析有向无环图DAG的Sugiyama层次布局 - 图12就相当于最小化伪节点的数量

image.png

在d3-dag中，作者引入了第三方库jsLPSolver来求解这个纯整数线性规划问题。

  1. import { Constraint, Solve, SolverDict, Variable } from "javascript-lp-solver";
  3. function simplexCall(dag: Dag<OpsNodeDatum<Ops>, OpsLinkDatum<Ops>>): void {
  4.     const variables: SolverDict<Variable> = {};
  5.     const ints: SolverDict<number> = {};
  6.     const constraints: SolverDict<Constraint> = {};
  8.       /** 获取节点ID */
  9.     function n(node: OpsDagNode<Ops>): string {
  10.         // ...
  11.     }
  13.     /** 获取节点的关联变量 */
  14.     function variable(node: OpsDagNode<Ops>): Variable {
  15.         // ...
  16.     }
  18.     /** 强制first节点在second节点之前
  19.      *
  20.      * @param prefix 确定描述约束的唯一前缀
  21.      * @param strict 严格在或可能相等之前
  22.      */
  23.     function before(
  24.       prefix: string,
  25.       first: OpsDagNode<Ops>,
  26.       second: OpsDagNode<Ops>,
  27.       strict: boolean = true
  28.     ): void {
  29.       const fvar = variable(first);
  30.       const svar = variable(second);
  31.       const cons = `${prefix}: ${n(first)} -> ${n(second)}`;
  33.       constraints[cons] = { min: +strict };
  34.       fvar[cons] = -1;
  35.       svar[cons] = 1;
  36.     }
  38.     // 初始化节点变量为子节点数量，且为整数变量
  39.     for (const node of dag) {
  40.       const nid = n(node);
  41.       ints[nid] = 1;
  42.       variables[nid] = {
  43.         opt: node.children.length
  44.       };
  45.     }
  47.     /** 可以插入自定义的排序或分组，这里省略相关逻辑 */
  49.     // 添加边限制
  50.     for (const link of dag.ilinks()) {
  51.       before("link", link.source, link.target);
  52.       ++variable(link.source).opt;
  53.       --variable(link.target).opt;
  54.     }
  56.     // 解线性规划
  57.     const { feasible, ...assignment } = Solve.call(
  58.       {},
  59.       {
  60.         optimize: "opt",
  61.         opType: "max",
  62.         constraint,
  63.         variables,
  64.         ints
  65.       }
  66.     );
  68.     // lp solver 赋值
  69.     for (const node of dag) {
  70.       node.value = assignment[n(node)] || 0;
  71.     }
  72.   }

image.png

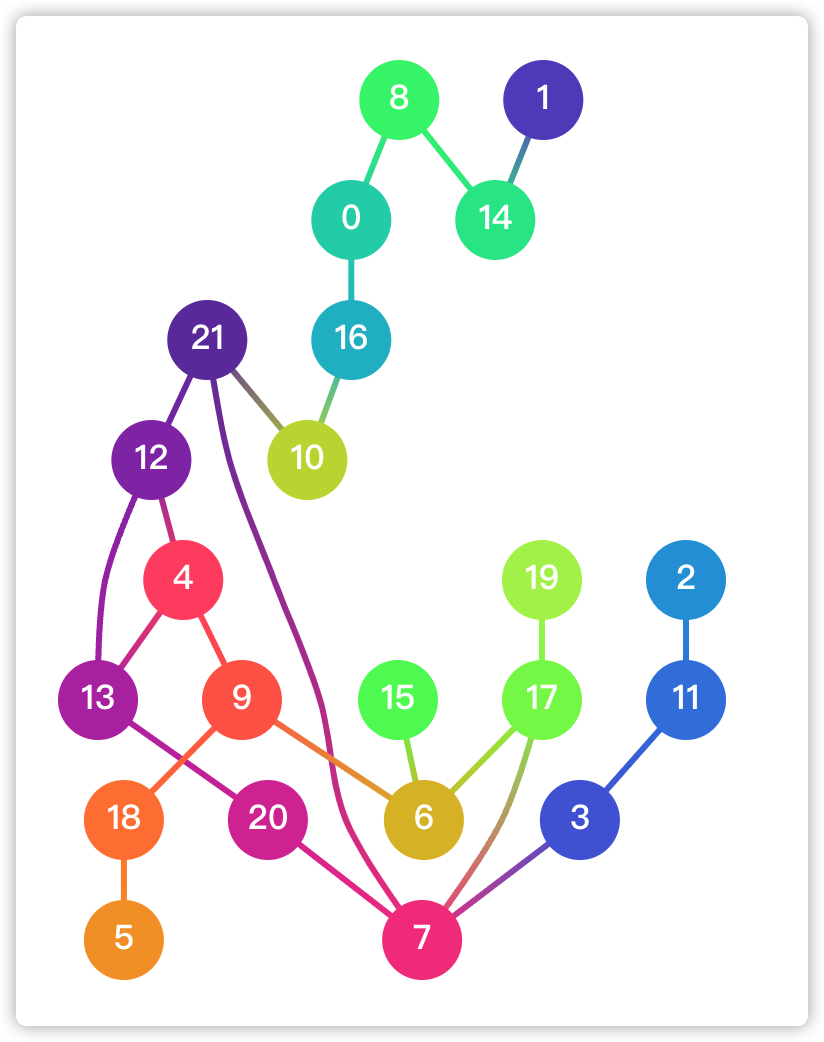
2. 减少边交叉

a. Two Layer - 两两比较

每两层进行排序来最小化交叉边，通常速度比较快，执行多次可以提升效果。

  • bigrams：以二元形式遍历，[1, 2, 3,4 ] => [1, 2], [2, 3], [3, 4]
  1. interface TwolayerOperator {(
  2.     topLayer: DagNode[],
  3.     bottomLayer: DagNode[],
  4.     topDown: boolean // 自顶向下，只重排序bottomLayer，topLayer不动，默认 true
  5. ): void
  7. options = {}
  8. function twoLayerCall(layers: OpSugiNode<O>[][]): void {
  9.     const reversed = layers.slice().reverse();
  11.     let changed = true;
  12.     for (let i = 0; i < options.passes && changed; ++i) {
  13.       changed = false;
  15.       // top down，每两层对下层排序
  16.       for (const [upper, bottom] of bigrams(layers)) {
  17.         const init = new Map(bottom.map((node, i) => [node, i] as const));
  18.         options.order(upper, bottom, true);
  19.         if (bottom.some((node, i) => init.get(node)) !== i) {
  20.           changed = true;
  21.         }
  22.       }
  24.       // bottom up，每两层对上层排序
  25.       for (const [lower, topl] of bigrams(reversed)) {
  26.         const init = new Map(topl.map((node, i) => [node, i] as const));
  27.         options.order(topl, lower, false);
  28.         if (topl.some((node, i) => init.get(node)) !== i) {
  29.           changed = true;
  30.         }
  31.       }
  32.     }
  33.   }

一个常用的order 启发式算子为aggregate，根据目标节点的父节点或子节点次序的值（例如平均数和中位数）来排序。在d3-dag中默认使用中位数排序。

  1. class Median implements Aggregator {
  2.   private vals: number[] = [];
  4.   add(val: number): void {
  5.     this.vals.push(val);
  6.   }
  8.   val(): number | undefined {
  9.     return median(this.vals);
  10.   }
  11. }
  13. const medianFactory = (): Aggregator => new Median();
  15. // 以下默认factory为medianFactory
  16. function aggCall(
  17.     topLayer: DagNode[],
  18.     bottomLayer: DagNode[],
  19.     topDown: boolean
  20.   ): void {
  21.     if (topDown) {
  22.       const incr = new Map(
  23.         bottomLayer.map((node) => [node, factory()] as const)
  24.       );
  25.       for (const [i, node] of topLayer.entries()) {
  26.         for (const child of node.ichildren()) {
  27.           // 每个下层节点汇总它所有父节点的当前次序
  28.           incr.get(child).add(i);
  29.         }
  30.       }
  31.       // 计算中位数作为当前层的最终次序
  32.       const aggs = new Map(
  33.         [...incr.entries()].map(([node, agg]) => [node, agg.val()] as const)
  34.       );
  35.       // 根据位置更新节点的次序
  36.       order(bottomLayer, aggs);
  37.     } else {
  38.       const inds = new Map(bottomLayer.map((node, i) => [node, i] as const));
  39.       const aggs = new Map(
  40.         topLayer.map((node) => {
  41.           // 每个上层节点汇总它所有子节点的当前次序
  42.           const agg = aggregate(
  43.             factory,
  44.             map(node.ichildren(), (child) => inds.get(child))
  45.           );
  46.           return [node, agg] as const;
  47.         })
  48.       );
  49.       order(topLayer, aggs);
  50. }
  1. 计算坐标

    a. Center

根据节点大小留出间距后让每层节点居中对齐排列，耗时非常短。

  1. function centerCall<N, L>(
  2.     layers: DagNode<N, L>[][],
  3.     nodeSize: CoordNodeSizeAccessor<N, L>
  4.   ): number {
  5.     // 计算每层的总宽度
  6.     const widths = layers.map((layer) => {
  7.       let width = 0;
  8.       for (const node of layer) {
  9.         const nodeWidth = nodeSize(node);
  10.         node.x = width + nodeWidth / 2;
  11.         width += nodeWidth;
  12.       }
  13.       return width;
  14.     });
  15.     const maxWidth = Math.max(...widths);
  16.     if (maxWidth <= 0) {
  17.       throw new Error("must assign nonzero width to at least one node");
  18.     }
  19.     for (const [i, layer] of layers.entries()) {
  20.       const width = widths[i];
  21.       const offset = (maxWidth - width) / 2;
  22.       // 每个节点加上相对最宽层的偏移量
  23.       for (const node of layer) {
  24.         node.x = node.x + offset;
  25.       }
  26.     }
  28.     return maxWidth;
  29.   }

DAG绘制

因为d3-dag仅提供了DAG数据结构和布局的能力，没有限制绘制的方法，以下是用d3.js绘制SVG的简单例子：

  1. import * as d3 from "d3";
  2. import * as d3dag from "d3-dag";
  4. const dag = d3dag.dagStratify()(data);
  5. const layout = d3dag
  6.     .sugiyama()
  7.     .layering(d3dag.layeringCoffmanGraham())
  8.     .decross(d3dag.decrossTwoLayer())
  9.     .coord(d3dag.coordCenter())
  10.     .nodeSize((node) => [node ? 60 : 10, 60]); // 节点和伪节点的间距
  12. const { width, height } = layout;
  14. // 容器
  15. const svg = d3.select("svg").attr("width", width).attr("height", height);
  17. // 节点
  18. const nodes = svg
  19.     .append("g")
  20.     .selectAll("g")
  21.     .data(dag.descendants())
  22.     .enter()
  23.     .append("g")
  24.     .attr("transform", ({ x, y }) => `translate(${x}, ${y})`);
  26. // 形状
  27. nodes.append("circle").attr("r", 20);
  29. // 文本
  30. nodes.append("text").text(({ data }) => data.id)
  31.     .attr("text-anchor", "middle")
  32.     .attr("alignment-baseline", "middle")
  33.     .attr("fill", "white");
  35. // 边
  36. const drawLine = d3.line().curve(d3.curveBasis).x((d) => d.x).y((d) => d.y);
  38. svg.append("g").selectAll("path").data(dag.links())
  39.     .enter().append("path")
  40.     .attr("d", ({ points }) => drawLine(points))
  41.     .attr("fill", "none")
  42.     .attr("stroke", "grey")
  43.     .attr("stroke-width", 3)

总结

Sugiyama层次布局方法提供了基础的布局思路和框架。经过多年的发展，针对不同的需求，各个环节都有很多算法可以灵活应用。限于篇幅，本文没有介绍其他算法的实现，有兴趣的可以查看参考资料中AntV G6的文章。

参考资料