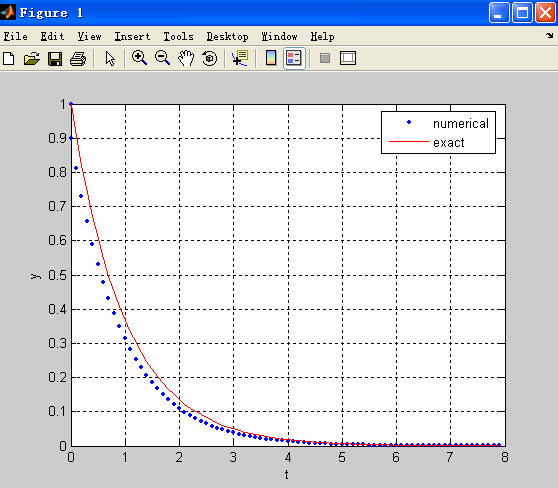
Exponential damping
function decaydt=0.1;lambda=1.0;n=80;t(1)=0;y(1)=1.0;for i=1:nt(i+1)=(i-1)*dt;f(i)=-lambda*y(i);y(i+1)=y(i)+dt*f(i);endfigure(1);plot(t,y,'b.',t,y(1)*exp(-lambda.*t),'r-');legend('numerical','exact');xlabel('t');ylabel('y');grid on;end%save as decay.m OR simply execute the function
Euler’s method 欧拉法
f(x,y)=y’(x,y)
公式:
fn-1=(xn-1,yn-1)
yn = yn-1 + hfn-1
Differential
y’=y-2x; initial condition y(0)=1
function [x p y]=euler(f,x0,y0,xn,n)
h=(xn-x0)/n;
x=x0:h:xn;
y(1)=y0;
p(1)=y0;
for i=1:n
p(i+1)=y(i)+h*f(x(i),y(i));
y(i+1)=y(i)+h/2*(f(x(i),y(i))+f(x(i+1),p(i+1)));
end
%save as euler.m
function calc
format long;
clear all;
x0=0;
xn=1;
y0=1;
n=10;
[x p y]=euler(@f01,x0,y0,xn,n);
z=sqrt(1+2*x);
figure(1);
plot(x,p,'r.',x,y,'b',x,z,'k--');
grid on;
end
%save as calc.m
function f=f01(x,y)
f=y-2*x/y;
x0=0;
xn=1;
y01=1;
end
%save as f.m
Execute
calc
gives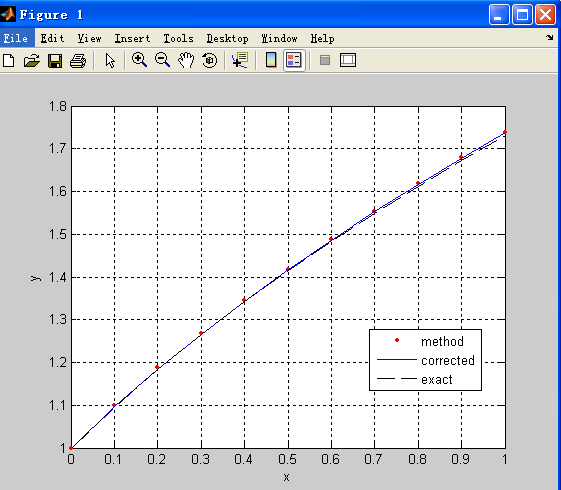
用WolframAlpha计算,精确解为2 - e^x + 2 x
Differential #2
y’=y+x+1 with initial condition y(0)=1
Simply change z to -2+3*exp(x)-x and and f to y+x+1
function calc
format long;
clear all;
x0=0;
xn=0.5;
y0=1;
n=10;
[x p y]=euler(@f01,x0,y0,xn,n);
z=-2+3*exp(x)-x;
figure(1);
plot(x,p,'r.',x,y,'b',x,z,'k--');
legend('method','corrected','exact');
xlabel('x');
ylabel('y');
grid on;
end
%save as calc.m
function f=f01(x,y)
f=y+x+1;
end
gives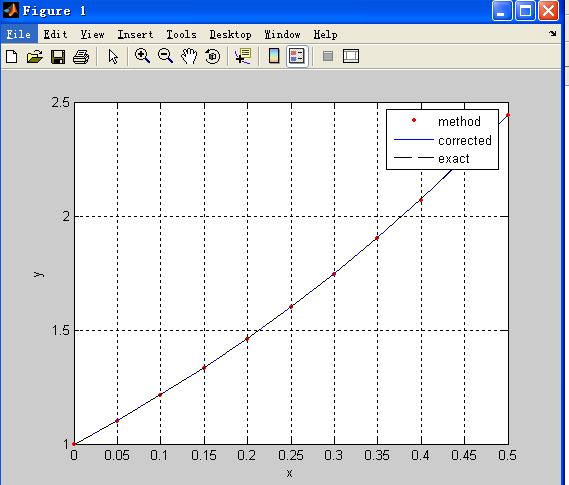
基本符合wolframAlpha解
Differential #3
y’=reciprocal(1+x^2)-2y^2 y(0)=0.
0<=x<=2.
Simply changes z to x./(1+x.^2) and f to 1/(1+x^2)-2*y^2 where dot. after x indicates element-wise operations( for x is a bunch of values which we call a matrix )
function f=f01(x,y)
f=1/(1+x^2)-2*y^2;
end
%save as f.m
function calc
format long;
clear all;
x0=0;
xn=2;
y0=0;
n=40;
[x p y]=euler(@f01,x0,y0,xn,n);
figure(1);
z=x./(1+x.^2);
plot(x,p,'r.',x,y,'b',x,z,'k--');
legend('method','corrected','exact');
xlabel('x');
ylabel('y');
grid on;
end
Change n from 10 to 20 and 40, (h from 0.2 to 0.1 and 0.05) gives respectively: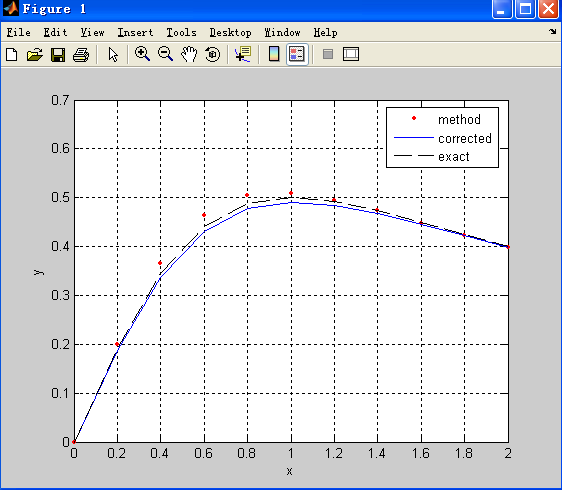

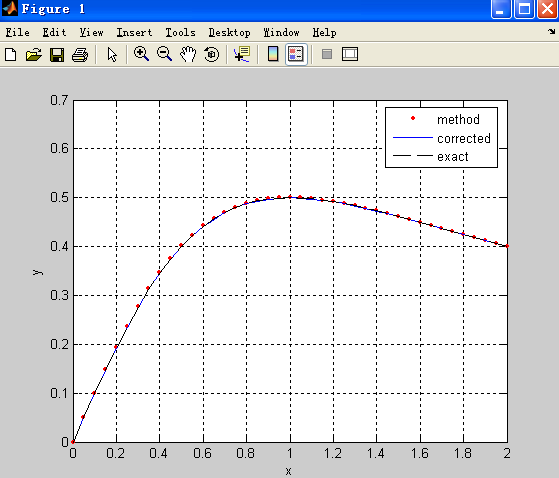
WolframAlpha
Different methods
Explicit and Implicit Euler’s method
function [x p y]=implicit(f,x0,y0,xn,n)
h=(xn-x0)/n;
x=x0:h:xn;
y(1)=y0;
p(1)=y0;
for i=1:n
p(i+1)=y(i)+h*f(x(i),y(i));
y(i+1)=y(i)+h*f(x(i+1),p(i+1));
end
%implicit.m
function calc1
format long;
clear all;
x0=0;
xn=1;
y0=1;
n=10;
[x p y]=implicit(@f01,x0,y0,xn,n);
z=exp(x);
figure(1);
plot(x,p,'r.',x,y,'b',x,z,'k--');
legend('---','implicit method','exact');
xlabel('x');
ylabel('y');
grid on;
end
function f=f01(x,y)
f=y;
end
execute calc1 gives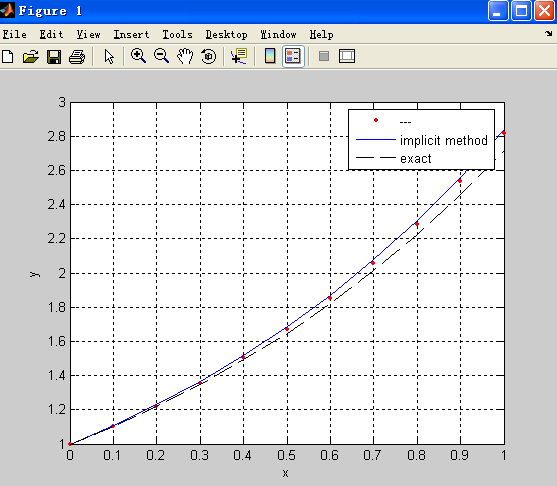
which is pretty close.
Trapzodial’s method
function [x p y]=trap(f,x0,y0,xn,n)
h=(xn-x0)/n;
x=x0:h:xn;
y(1)=y0;
p(1)=y0;
for i=1:n
p(i+1)=y(i)+h*f(x(i),y(i));
y(i+1)=y(i)+0.5*h*(f(x(i),y(i))+f(x(i+1),p(i+1)));
end
%save as trap.m
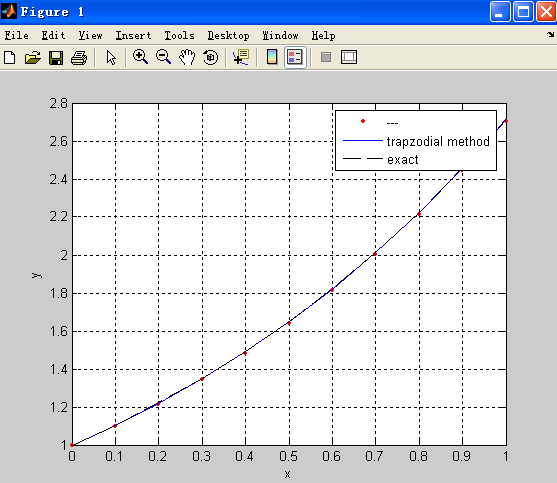
Double increments’ method
function [x p y]=double(f,x0,y0,xn,n)
h=(xn-x0)/n;
x=x0:h:xn;
y(1)=y0;
p(1)=y0;
for i=1:n
y(2)=y(1)+h*f(x0,y(1));
p(i+1)=y(i)+h*f(x(i),y(i));
y(i+1)=y(i)+h*f(x(i),y(i));
end
%double.m
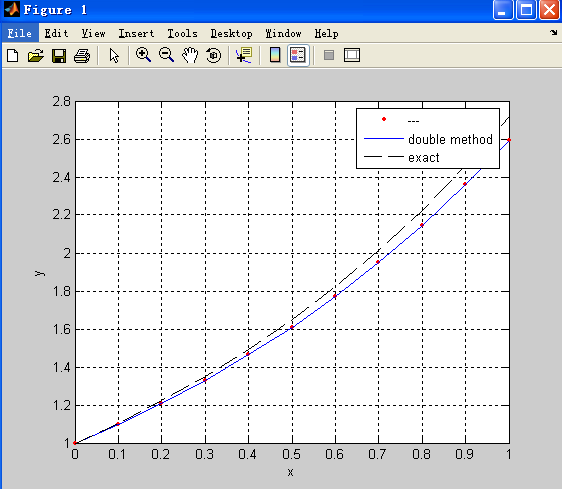
Differential #4
For y’=x-y+1 and y(0)=1
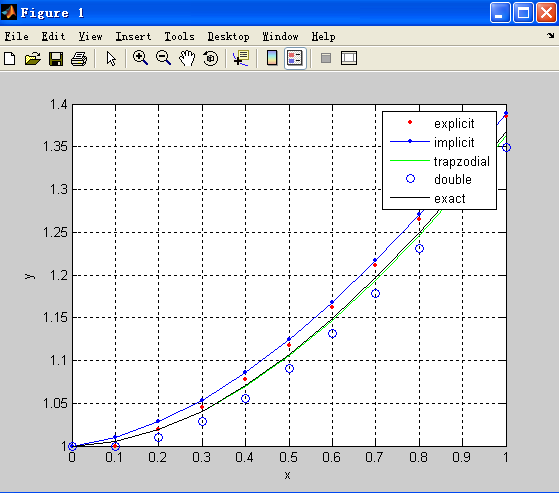
Combining all the different ways:
function f=f01(x,y)
f=x-y+1;
end
%save as f.m
function [x p y t d]=general(f,x0,y0,xn,n)
h=(xn-x0)/n;
x=x0:h:xn;
t(1)=y0;
d(1)=y0;
y(1)=y0;
p(1)=y0;
for i=1:n
p(i+1)=y(i)+h*f(x(i),y(i)); %Explicit
y(i+1)=y(i)+h*f(x(i+1),p(i+1)); %Implicit
t(i+1)=t(i)+0.5*h*(f(x(i),t(i))+f(x(i+1),p(i+1))); %trapzodial
d(2)=d(1)+h*f(x0,d(1));
d(i+1)=d(i)+h*f(x(i),d(i)); %double inc
end
%save as general.m
function calc
format long;
clear all;
x0=0;
xn=1;
y0=1;
n=10;
[x p y t d]=general(@f01,x0,y0,xn,n);
z=x+exp(-x);
figure(1);
plot(x,p,'r.',x,y,'b.-',x,t,'g-',x,d,'o',x,z,'black');
legend('explicit','implicit','trapzodial','double','exact');
xlabel('x');
ylabel('y');
grid on;
end
%save as calc.m
RK-4#1
Solve y’=xsqrt(y) in [2,3] numerically using Runge-Kutta methods
function y=rk4(f,a,b,ya,n)
h=(b-a)/n;
x=a:h:b;
y(1)=ya;
for i=1:n
k1=h*feval(f,x(i),y(i));
k2=h*feval(f,x(i)+h/2,y(i)+k1/2);
k3=h*feval(f,x(i)+h/2,y(i)+k2/2);
k4=h*feval(f,x(i)+h,y(i)+k3);
y(i+1)=y(i)+(k1+2*k2+2*k3+k4)/6;
end
%save as rk4.m
function f=f01(x,y)
f=x*sqrt(y);
end
%save as f01.m
function calc1
clc;clf;clear all;
n=11;
a=2;
b=3;
ya=4;
y(1)=4;
h=(b-a)/n;
x=a:h:b;
y=rk4(@f01,2,3,4,11);
xe=linspace(a,b,100);
ye=(1+0.25*xe.*xe).^2;
figure(1);
plot(xe,ye,'-',x,y,'o');
legend('Exact','Numerical');
grid on;
end
gives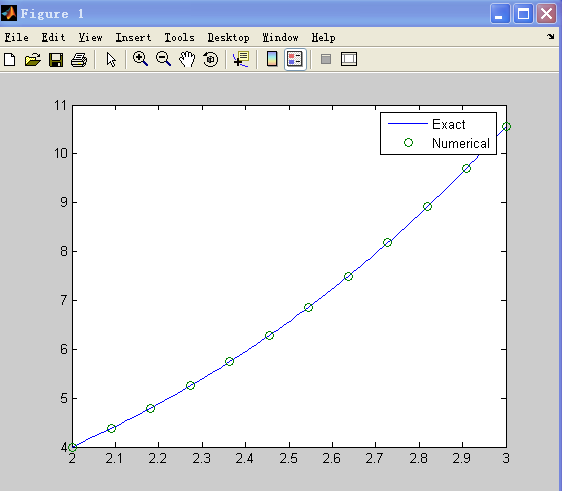
WolframAlpha 求解… 怎么有两个答案啊!!
RK-4#2
Similarly, for y’=y^2; y(0)=1
function f=f01(x,y)
f=y*y+0*x;
end
function calc1
clc;clf;clear all;
n=6;a=0;b=0.5;
ya=1;y(1)=1;
h=(b-a)/n;
x=a:h:b;
y=rk4(@f01,a,b,1,n);
xe=linspace(a,b,100);
ye=1./(1-xe);
figure(1);
plot(xe,ye,'-',x,y,'o');
legend('Exact','Numerical');
grid on;
end
gives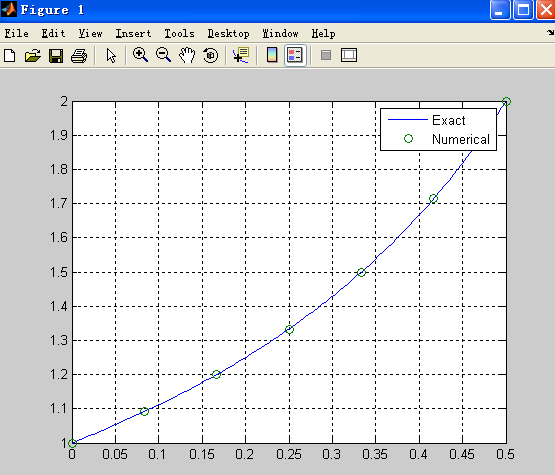
WolframAlpha 求解,答案为 1/(1-x)、
RK-4#3
function [to,yo]=rk4s(fun,tspan,y0,n)
t0=tspan(1);
tf=tspan(2);
h=(tf-t0)/n;
t=t0;
y=y0(:);
to=t;
yo=y.';
while (t<tf)
if t+h>tf,
h=tf-t;
end
s1=feval(fun,t,y);
s1=s1(:);
s2=feval(fun,t+h/2,y+h*s1/2);
s2=s2(:);
s3=feval(fun,t+h/2,y+h*s2/2);
s3=s3(:);
s4=feval(fun,t+h,y+h*s3);
s4=s4(:);
t=t+h;
y=y+h*(s1+2*s2+2*s3+s4)/6;
to=[to;t];
yo=[yo;y.'];
end
(:) transpose a vector to column vector
function f=f02(x,y)
f=[y(2);2*y(2)-2*y(1)+exp(2*x)*sin(x)];
end
function calc2
[x,y]=rk4s(@f02,[0,1],[-0.4;-0.6],40);
figure(1);
plot(x,y(:,1))
grid on;
end
第一个向量为区间,第二个是y’ y’’在前面左边区间处的初始值
Somehow gives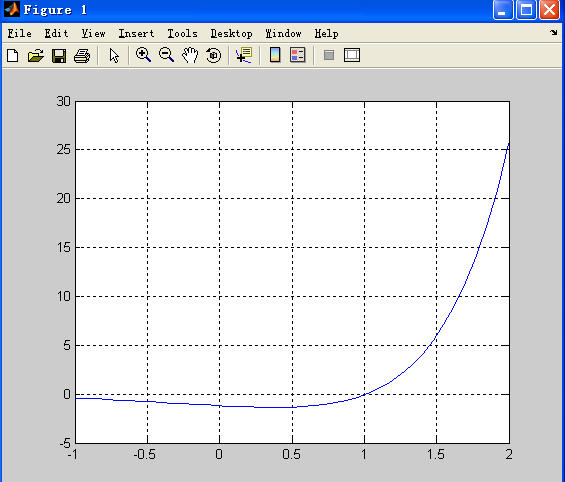
WolframAlpha 给出类似结果
RK-4#4
function f=f02(x,y)
f=[y(2);-y(1)+0*y(2)];
end
function calc2
[x,y]=rk4s(@f02,[pi,6],[0;3],40);
figure(1);
plot(x,y(:,1))
grid on;
end
gives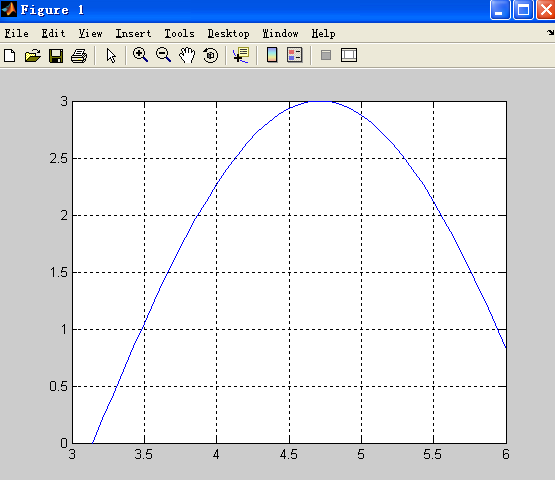
与答案 -3sin(x) 接近
function y=bvpt(u,v,w,f,x,y1,yn,n)\
h=(x(n)-x(1))/(n-1);
a(1:n)=u(1:n)-0.5*h*v(1:n);
b(1:n)=h*h*w(1:n)-2*u(1:n);
c(1:n)=u(1:n)+0.5*h*v(1:n);
d(1:n)=h*h*f(1:n);
a(1)=0;
b(1)=1;
c(1)=0;
d(1)=y1;
a(n)=0;
b(n)=1;
c(n)=0;
d(n)=yn;
y=tri(a,b,c,d);
end
function calc1
[x y]=ode23(@f21,[0,1],[-0.4;-0.6])
figure(1);
plot(x,y(:,1),'r',x,y(:,2));
xlabel('x');
ylabel('y');
legend('y','dy');
grid on;
end
function calc2
clear all;
clc;
format long;
x1=2;
xn=3;
n=100;
y1=0;
yn=0;
h=(xn-x1)/(n-1);
x=x1:h:xn;
u(1:n)=-1;
v(1:n)=0;
w(1:n)=2./x(:)./x(:);
f(1:n)=1./x(:);
y=bvpt(u,v,w,f,x,y1,yn,n);
figure(1);
plot(x,y);
grid on;
end
function dy=f21(x,y)
dy=[y(2);2*y(2)-2*y(1)+exp(2*x)*sin(x)];
end