Matlab differential and integral

点数值微分

function df=mulpt(func,x0,h,type)
y0 =subs(sym(func),findsym(sym(func)),x0);
y1 =subs(sym(func),findsym(sym(func)),x0+h);
y2= subs(sym(func),findsym(sym(func)),x0+2*h);
y_1= subs(sym(func),findsym(sym(func)),x0-h);
y_2= subs(sym(func),findsym(sym(func)),x0-2*h);
switch type
    case 1,
        df =(y1-y0)/h;
    case 2,
        df=(y0-y_1)/h;
    case 3,
        df=(y1-y_1)/(2*h);
    case 4,
        df=(-3*y0+4*y1-y2)/(2*h);
    case 5,
        df=(3*y0-4*y_1+y_2)/(2*h);
end
%save as mulpt.m

execute with

clear all;
format long;
f=inline('sqrt(x)');
x0=4;
mulpt(f,x0,1e-3,3)

gives

ans =

   0.25000000195319

此程序旨在计算x0处的导数。用WolframAlpha计算，发现结果十分接近。

段数值微分

execute with

clear all;
format long;
x=0:pi/16:pi;
y=sin(x);
yp=cos(x);
df1=mulpt('sin(x)',x,pi/64,1);
df3=mulpt('sin(x)',x,pi/64,3);
figure(1);
plot(x,df1,'r-',x,df3,'g.-',x,y,'b--',x,yp,'o');
grid on;
xlabel('x');
ylabel('y');

gives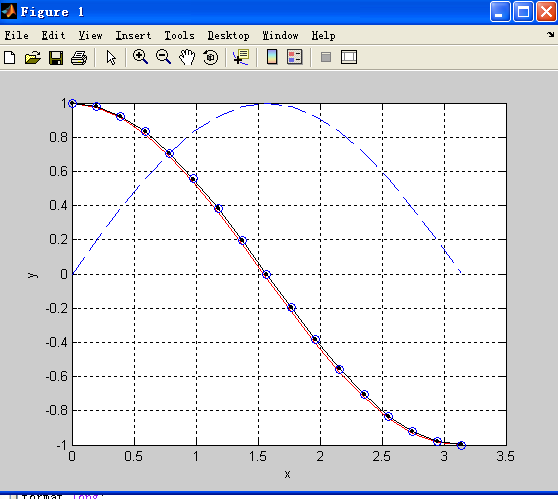

图中：红线，黑线-黑点分别为前差，中心差计算得到的图像。上分蓝色虚线为函数，分离的蓝色小圈为导数。

Trapezoid/Simpson Rule approx. integral

Trapezoial method
参见计算物理学 p.80 TrapInt1.m

function t=trapint(f,a,b,nsub)
n=nsub+1;
h=(b-a)/nsub;
x=a:h:b;
y=f(x);
t=h*(0.5*y(1)+sum(y(2:n-1))+0.5*y(n));
end

%save as trapint.m

Execute with

clear all;
format long;
f=inline('cos(x)');
trapint(f,0,pi/2,100)

gives

ans =

   0.99997943823961

Simpson’s Rule 参见计算物理学 p.81 SimpInt1.m

function s=simpint(f,a,b,ndsub)
n=ndsub+1;
h=(b-a)/(n-1);
x=a:h:b;
y=f(x);
s=(h/3)*(y(1)+4*sum(y(2:2:n-1))+2*sum(y(3:2:n-2))+y(n));
end

execute with

clear all;
format long;
f=inline('cos(x)');
simpint(f,0,pi/2,100)

gives

ans =

   1.00000000033824

合并起来，两段分别相加：
Execute with

clear all;
format long;
f=inline('cos(x)');
t=trapint(f,0,pi/4,100);
s=simpint(f,pi/4,pi/2,100);
t+s

e^(-x2) 积分

Define integrand

function y=integrand(x)
y=exp(-x*x);
end

Trapzoid’s method:
Execute with

a=-1e4;b=1e4;n=1e6;h=(b-a)/n;
int=integrand(a);
for i=2:n
    int=int+2*integrand(a+(i-1)*h);
end
int=h/2*(int+integrand(b));
format long
int

gives
int =

1.77245385090551
%all digits perfectly matched

Simpson’s method:
Execute with

a=-1e4;b=1e4;n=1e6;h=(b-a)/(2*n);
int=integrand(a);
for i=1:n
    int=int+4*integrand(a+(2*i-1)*h);
end
for j=1:n-1
    int=int+2*integrand(a+1*j*h);
end
int=h/3*(int+integrand(b));
format long
int

gives
int =

           1.76912051757233<br />_%only one digit matched_

和WolframAlpha计算结果(1.7724538509055160272981674833)对比，发现前者效果更好。