Matlab Eq solving

Bisection method (old-fashioned)

function r=bisect(f,a,b,eps)
n=1+round((log(b-a)-log(eps))/log(2))
fa=feval(f,a);
fb=feval(f,b);
for i=1:n
    c=(b+a)/2;
    fc=feval(f,c);
    if fc*fa<0
        b=c;
        fb=fc;
    else
        a=c;
        fa=fc;
    end
end
r=c;
%SAVE AS bisect.m

注意，这里feval(Fcuntion EVALuate) 用法为 feval(function, argument1, argument2…)，相当于将argument1，argument2……作为变量输入到function中并计算。
比如feval(f,2);
其中f=x^2;
则
feval(f,2) ==> 4。
注意，这里inline为创建行内(inline)函数。
注意，这里初始区间需要人为给定，下面将会给a，b初始区间的范围
When executing with

%IMPUT AS COMMANDS


>> format long
>> f=inline('exp(x)*log(x)-x*x');
>> eps=1e-5;
>> a=1;
>> b=2;
>> bisect(f,a,b,eps)

Result：

bisect(f,a,b,eps)

n =

    18


ans =

   1.69459915161133

Secant method （old-fashioned)

function r=secant(f,x0,x1,eps,nmax)
dx=x1-x0;
n=0;
while((abs(dx)>=eps) & (n<nmax))
    x2=x1-f(x1)*(x1-x0)/(f(x1)-f(x0));
    if(f(x0)*f(x2)>0)
        dx=x2-x0;
        x0=x2;
    else
        dx=x2-x1;
        x1=x2;
    end
    n=n+1;
end
r=x2

%SAVE AS secant.m

when executing with

format long;
>> x0=1.0;
>> x1=2.0;
>> eps=0.000001;
>> nmax=100;
>> secant(f,x0,x1,eps,nmax)

gives

secant(f,x0,x1,eps,nmax)

r =

   1.69460080240014


ans =

   1.69460080240014

Newton’s matrix method

function [x n]=newton(x0)
x1=x0-f(x0)/df(x0);
n=1;
while (norm(x1-x0)>=1e-6) & (n<=1000)
    x0=x1;
    x1=x0-f(x0)/df(x0);
    n=n+1;
end
x=x1
n
end

%SAVE AS newton.m

function y=f(x)
y(1)=x(1)-0.7*sin(x(1))-0.2*cos(x(2));
y(2)=x(2)-0.7*cos(x(1))+0.2*sin(x(2));
end

%save as f.m

function y=df(x)
y=[1-0.7*cos(x(1)) 0.2*sin(x(2));
  0.7*sin(x(1)) 1+0.2*cos(x(2))];
end

%save as df.m

注意这里牛顿法，参照计算物理学（刘金远）公式 2.2.11，所要求解的答案中，A*d=B；其中A为导数矩阵，分别为对x，y的偏导数矩阵（人工求解, df.m 2 by 2 matrix），而B为函数（人工输入 f.m 1 by 2 vector），d为所求答案矩阵，做除法即可。
Executing with

x0=[0.5 0.5]
newton([0.5 0.5])

gives

x =

   0.52652301348344   0.50791962157383


n =

    12


ans =

   0.52652301348344   0.50791962157383

Gradient desent

function [x n f]=dsense(x0)
eps=1.0e-6;
x=x0;
[f f2 g g2]=myfun(x);
lambda=f2/g2;
x=x-lambda*g;
n=0;
while (norm(x-x0)>=eps)
    x0=x;
    n=n+1;
    [f f2 g g2]=myfun(x);
    lambda =f2/g2;
    x=x-lambda*g;
    if(n>100000)
        disp('WRONG');
        return;
    end
end
end

%save as dsense.m

%FUNCTION DEFINE
function [f f2 g g2]=myfun(x)
f(1)=x(1)-5*x(2)*x(2)+7*x(3)*x(3)+12;
f(2)=3*x(1)*x(2)+x(1)*x(3)-11*x(1);
f(3)=2*x(2)*x(3)+40*x(1);
f=[f(1) f(2) f(3)];
f2=f(1)*f(1)+f(2)*f(2)+f(3)*f(3);

g(1)=2*f(1)+2*f(2)*(3*x(2)+x(3)-11)+2*40*f(3);
g(2)=2*f(1)*(-10*x(2))+2*f(2)*(3*x(1))+2*f(3)*(2*x(3));
g(3)=2*f(1)*(14*x(3))+2*f(2)*(x(1))+2*f(3)*(2*x(2));
g=[g(1) g(2) g(3)];
g2=g(1)*g(1)+g(2)*g(2)+g(3)*g(3);
end\

%save as myfun.m

参见计算物理学（刘金远）公式(2.2.20)，给定初始值(x,y,z);
executing with

x0=[-1.5 6.5 -5.0]
dsense(x)

gives

ans =

   1.00001447533909   5.00003436406575  -4.00003033024421

注意，如果结果出现wrong，很可能为函数给定部分myfun.m 哪一步出错了。
用wolframalpha.com求解，发现所得答案正式4组实数解中的一组
另外，由于这种局域数值计算法极度依赖于初始条件，不同的初始条件会给出来不同的解，在选定初始条件的时候，有时候需要大片撒网观察其输出情况；用人话说:

假如函数是蛋托形状的：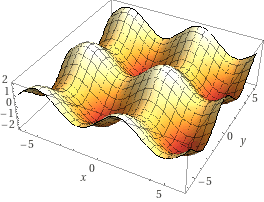

在上面放一个小球，小球最终会滑到临近的坑里，由于这个蛋托有很多坑（一个坑就是一个解），所以小球滚到哪个坑里（输出哪个数值解）与初始放小球的位置（初始条件选取）有关。

General Iteration Method (error occurred)

function [x, y]=iteration(x0,y0)
x=x0;
y=y0;
n=1;
while n<3
    x1=(1/2)*(x*x-y+0.5);
    y1=(1/8)*(x*x+4*y*y+8*y-4);
    n=n+1;
    x=x1
    y=y1
end
end

%save as iteration.m

An error occurred as iteration tiem n increases (x and y diverges quickly)