DBSCAN：Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法。

DBSCAN 是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间是紧密相连的，也就是说，在该类别任意样本周围不远处一定有同类别的样本存在。
通过将紧密相连的样本划为一类，这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别，则我们就得到了最终的所有聚类类别结果。

前置概念

假设样本集为聚类算法 - DBSCAN - 图1 ，定义下面几个概念：

-邻域：对于，其-邻域包含样本集中与的距离不大于的样本（包括自己），即，这个子样本集的个数记为
核心点（core point）：对于任，如果其-邻域至少包含个样本，即，则是一个核心点。
边界点（border point）：对于任，若其不是一个核心点，但位于一个或多个核心点的-邻域内，则是一个边界点。

离群点（outlier）：对于任聚类算法 - DBSCAN - 图19 ，若其既不是核心点也不是边界点，则它是一个离群点。

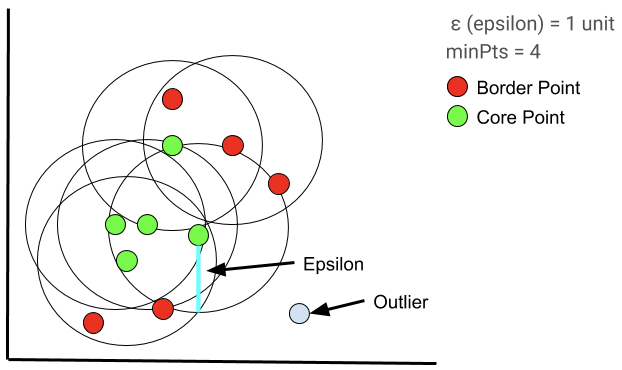
 ![image.png](https://cdn.nlark.com/yuque/0/2021/png/2070905/1616759231465-408c1619-7d0b-4a80-bf28-a89b7ef39c0e.png#height=278&id=C11EB&margin=%5Bobject%20Object%5D&name=image.png&originHeight=370&originWidth=622&originalType=binary&ratio=1&size=36064&status=done&style=none&width=467)

密度直达（directly density-reachable）：若位于的-邻域中，且是一个核心点，则称由密度直达。注意：除非也是核心点，否则此时不能说由密度直达，密度直达不具有对称性。
密度可达（density-reachable）：对于和，若存在样本序列，其中，，且由密度直达，则称由密度可达。此时序列中的传递样本均为核心点，因为只有核心点才能使其他样本密度直达。注意：密度可达也不满足对称性，这个可以由密度直达的不对称性得出。
密度相连（density-connected）：对于和，若存在使得和均由密度可达，则称和密度相连。注意：密度相连是满足对称性的。

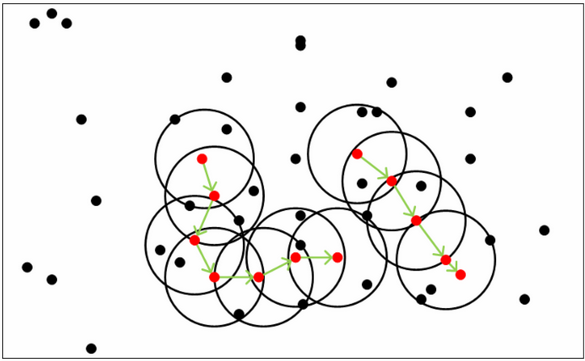
以下图为例，图中聚类算法 - DBSCAN - 图47 。红色的点都是核心点，因为其聚类算法 - DBSCAN - 图48 -邻域至少有 5 个样本，黑色的样本是非核心点。所有核心点密度直达的样本在以红色核心点为中心的超球体内，如果不在超球体内，则不能密度直达。图中用绿色箭头连起来的核心点组成了密度可达的样本序列，在这些密度可达的样本序列的聚类算法 - DBSCAN - 图49 -邻域内所有的样本相互都是密度相连的。

算法原理

DBSCAN 的原理描述起来很简单：任选一个没有类别的核心点作为种子，找到该核心点能够密度可达的样本集合，即为一个聚类簇。接着继续选择另一个没有类别的核心点去寻找密度可达的样本集合，这样就得到另一个聚类簇。一直运行到所有核心点都有类别为止。

算法的输入：

样本集

:::info 距离的度量一般使用欧式距离。 :::

:::warning 某些非核心点可能同时位于两个（或多个）核心点的聚类算法 - DBSCAN - 图54 -邻域内，但这两个核心点并不密度直达（也就是说不属于同一个聚类簇），那么如何界定该非核心点属于哪个聚类簇呢？
一般来说，此时 DBSCAN 采用先来后到的方法，该非核心点会被分配给先进行聚类的那个簇。
因此，DBSCAN 并不是完全稳定的算法。 :::

代码实现

导包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles, make_moons

生成测试数据：

X1, y1 = make_circles(n_samples=500, factor=0.4, noise=0.1)
X2, y2 = make_moons(n_samples=300, noise=0.1)
X2 = X2 + np.array([2.2, 1])
X = np.vstack((X1, X2))

画图观察数据：

plt.scatter(X[:, 0], X[:, 1])
plt.show()

实现 DBSCAN：

### 输入参数
eps = 0.15
min_pts = 5
### 辅助变量、结果变量
cluster_no = np.full(X.shape[0], -1)    # X 中每个样本所属的簇的编号。先全部初始化为 -1，-1 代表不属于任何簇
clusters_count = 0                        # 簇的个数
core_points_and_neighbors = {}            # 所有核心点及其邻域内的点（索引）。key 为核心点（索引），value 是一个列表，包含该核心点的邻域内的所有点（索引）
all_core_points = []                    # 所有核心点（索引）
not_visited_core_points = []            # 所有未访问过的核心点（索引）
visited_points = []                        # 已访问过的点（索引）
### 找出所有核心点及其邻域内的点
for i, o in enumerate(X):
    distance_square = np.sum((o - X) ** 2, axis=1)            # 算出点 o 与所有点的距离的平方
    neighbors = np.where(distance_square <= eps ** 2)[0]    # 点 o 的邻域内的所有点（索引），注意：这其中包括点 o 自己
    if len(neighbors) >= min_pts:
        core_points_and_neighbors[i] = neighbors
all_core_points = list(core_points_and_neighbors.keys())    # 所有核心点（索引）
not_visited_core_points = all_core_points.copy()            # 所有未访问过的核心点（索引）
### 每轮循环随机找一个未访问过的核心点，以该点为中心进行广度优先搜索，
### 找出该点能密度可达的所有点，这些点就组成了一个簇。
### 当所有核心点都被访问过一次后，跳出循环。
while len(not_visited_core_points) > 0:
    ### 创建一个队列，用于广度优先搜索。随机选取一个未访问过的核心点放入队列中
    core_point = np.random.choice(not_visited_core_points)    # 随机选取一个核心点（索引）
    queue = [core_point]                                    # 初始化队列
    not_visited_core_points.remove(core_point)
    ### 利用队列进行广度优先搜索。
    ### 每轮循环从队首取出一个点，如果该点是核心点，将其邻域内的所有未访问过的点加入队尾，
    ### 直到队列为空，搜索结束，这些搜索到的所有点组成一个簇。
    while len(queue) > 0:
        point = queue.pop(0)                # 取出队首的点（索引）
        ### 不管是不是核心点，执行下面两行代码
        cluster_no[point] = clusters_count    # 设置簇号
        visited_points.append(point)        # 添加到已访问列表
        ### 如果该点是核心点
        if point in all_core_points:
            if point in not_visited_core_points:
                not_visited_core_points.remove(point)    # 从“未访问过的核心点”列表中删除
            queue.extend([neighbor for neighbor in core_points_and_neighbors[point] if neighbor not in visited_points and neighbor not in queue])   # 将该点的邻域内所有未访问过的点加入队列，队列中已有的不重复加入
    clusters_count += 1     # 簇的个数加一

可视化展示聚类结果：

for i in range(-1, clusters_count):
    points = X[cluster_no == i]
    plt.scatter(points[:, 0], points[:, 1])
plt.show()

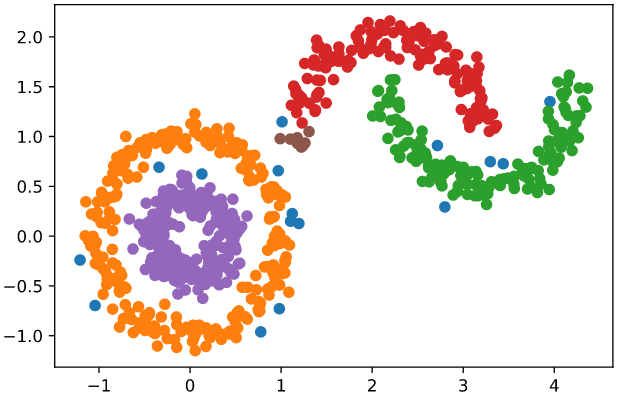:::info 图中蓝色的点是离群点，不属于任何簇。 :::

超参数的选择

TODO

如何评价结果好坏

TODO

算法优缺点

优点：

可以对任意形状的稠密数据集进行聚类，相对的，K-Means 之类的聚类算法一般只适用于凸数据集。
可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
聚类结果基本稳定，相对的，K-Means 之类的聚类算法初始值对聚类结果有很大影响。

缺点：

有 2 个超参数，因此调参比 K-Means 更复杂，因为要对 2 个超参数联合调参。
如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用 DBSCAN 聚类一般不适合。
样本集较大时，花费时间较长。

Cards

聚类算法 - DBSCAN