图形学 - 模型绘制 - 《Blog》

开篇
基础图元
平面图形-2D
立体模型-3D
- 立方体
- 球体
复杂多面体
- 一支保龄球
- 一张人脸
总结

开篇

本篇博文持续在webgl中绘制各种图形。在阅读本文时，你需要对基本的webgl有认识，并且熟悉中学书序的基本数学公式。不过这些公式都非常简单，只要你学过，使用起来就没有问题。我们的世界的物体都是有形状的，有些是圆的，有些是方的，还有些则是一些不规则的形状。计算机的时间就需要用特定的绘制方法模拟生产现实世界的各种图形。在计算机中，基本的绘制只能绘制三种几何体，点，线和面，其他所有的一切形状都是由这三种基本的图像通过在空间排列的方式组合而成的。我们如果要画任意一个物体，总共就两个步骤，第一画出基本的图像，第二确定他们再立体空间中的位置，剩下的就交给GPU给我们进行装配和光栅化。其中起一点很简单，一下我的主要是将第二点。如何通过集合数据计算，安排这些基础形状的位置。当然，以上只是我对画图的总结，这其中设计的webgl一些底层的东西需要你自己去学习。所以在读这篇文章的时候，你需要一些webgl和javascript的基础。这篇博文作为持续更新的作品，主要是用来告诉我们自己在使用各种框架画出缤纷世界时，不应该忘记这些构建这个时间的基石。本篇博文的所有示例均在这个网站展示，所有源码也会该网站上贴出。

基础图元

点

在webgl中点是构成任何元素的图形的基本要素，通常画一个点比较简单，我们只需要初始化着色器，建立上下文即可。点的绘制使用drawArrays方法，传入webgl.POINTS常量。画一个点是webgl入门的基本操作之一。

const vertex = new Float32Array([0.0, 0.0, 0.0]);
...
webgl.drawArrays(webgl.POINTS, 0, 1);

线

线是由无数个点构成的，在webgl中画线也非常简单，只需要制定一个起始点和一个结束点即可。下面我们就来画两条直线。

// 初始化两条点 A1 A2
const vertex = new Float32Array([0.5, 0.0, 0.0, -0.5, 0.0, 0.0, 0.0, 0.5, 0.0]);
const color = new Float32Array([1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0]);
...
webgl.drawArrays(webgl.LINES, 0, 4);

三角形

三角形是基础图元的最后一种图形，也是绘制所有复杂图形的基础。计算机的所有图形都是有三角形绘制的，这是因为在一个空间中，三个点只能确定一个面，而面是构成体的基本要素。三角形的绘制也非常简单，定义三个顶点。

const vertex = new Float32Array([
 0.5, 0.0, 0.0,
 -0.5, 0.0, 0.0,
 0.0, 0.5, 0.0
]);
...
webgl.drawArrays(webgl.TRIANGLES, 0, 3);

平面图形-2D

结束完基本图形的绘制，现在开始画质由基础图元拼接组成的平面。需要说明的是复杂的图形的绘制方式有许许多多种，我们只展示其中一种即可。你也可以按照不同的方法去绘制图形。一般来说你绘制的图形最好是越少占用存储空间越好。通过设置drawArrays的绘制方式我们可以决定如何去绘制我们的图形。下面的这些方式的截图：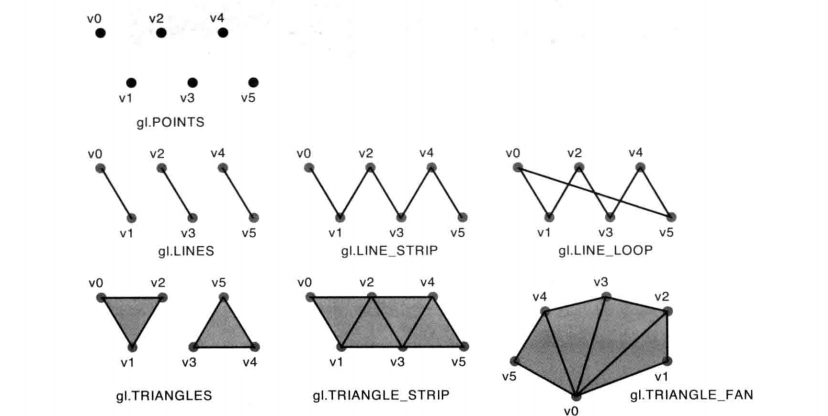

矩形

矩形绘制很简单，原理是：任何的矩形都是由两个三角形拼接而成。我们只需要按照顺序，画出两个三角形即可。这里我们使用的是wegbl.TRIANGLE_STRIP方式绘制。它的绘制步骤是0,1,2画出第一个三角形，然后是1,2,3绘制出第二个三角形。

const vertex = new Float32Array([ 
        0.0, 0.3, 0.0, // 1
        0.0, 0.0, 0.0, // 2
        0.3, 0.3, 0.0, // 3
        0.3, -0.3, 0.0 // 4
    ]);
...
 webgl.drawArrays(webgl.TRIANGLE_STRIP, 0, 4);

五角星

五角星的思路和扇形的思路是一致的，不过，我们仔细观察五角星就会发现，一个五角星其实是有10个顶点的。我们以五角星的中心为原点，链接每个顶点，就会画出五条短线和长线。最远的点就是五角星的五个角，最短的点就是离中心最近的那五个顶点。利用简单的数学公式，就可以求出每个顶点的位置。

//一共十个点
    const counts = 10,
        // 最远的点和最短的点到中心的距离
        radius = 0.45,
        min_radis = 0.25,
        //将夹角转换成弧度
        radiation = (Math.PI / 180) * (360 / 10),
        //中心位置
        center = [0.0, 0.0];
    let vertexs: number[] = center;
    let color: number[] = [1.0, 1.0, 0.0];
    for (let index = 0; index <= counts; index++) {
        // 顶点的位置
        let x = Math.sin(radiation * index) * radius;
        let y = Math.cos(radiation * index) * radius;
        // 内圈顶点的位置
        if (index % 2 === 0) {
            x = Math.sin(radiation * index) * min_radis;
            y = Math.cos(radiation * index) * min_radis;
        }
        vertexs.push(x);
        vertexs.push(y);
        color.push(...[1.0, 1.0, 0.0]);
    }
...
 webgl.drawArrays(webgl.TRIANGLE_FAN, 0, count);

窗格

描述三维物体时需要有地面参照，一个格子地板通常是很好的选择。假设我们需要画一个10 10 的地板，由100个格子组成，每个格子就是1 1 的宽和高。我们实际上是要画 10 10 2 个三角形。三角剖分如下图所示：

我们采用triangle-strip的方式，画质三角形，代码如下所示：

function createVertex (square:number) {
    square =  square * 10;
    let vertex:number[] = [];
    let pointer: number[] = [];
    let linePointer: number[] = [];
      // 画出每个格子在x和z轴上的点
    for (let indexX = 0; indexX < square; indexX++) {// x 
        for (let indexZ = 0; indexZ < square; indexZ++) {// z 
            vertex.push(indexX * 0.1,  0, -indexZ * 0.1);
        }
        linePointer.push(indexX * square, (indexX + 1) * square - 1);
    }
        // 画出通过TRIANGLE_STRIP 的方式指定索引
    for (let indexX = 0; indexX < Math.pow(square, 2) - square; indexX++) {// z 
        pointer.push(indexX, indexX + square);
    }
   // 三角形描边
    linePointer = linePointer.concat(pointer);
    return {
        vertexArray: new Float32Array(vertex),
        pointerArray: new Uint16Array(pointer),
        pointerLineArray: new Uint16Array(linePointer),
        count: pointer.length,
        lineCount: linePointer.length
    };
}
....
webgl.drawElements(webgl.TRIANGLE_STRIP, count, webgl.UNSIGNED_SHORT, 0);
webgl.drawElements(webgl.LINES, lineCount, webgl.UNSIGNED_SHORT, 0);

画出最终图形后，我们需要把地板进行平移，以保证我们的地板是在画布中居中显示的。

圆形

圆形的画法有很多种，我们用最简单的，即五角星的翻版，把五角星的短边都拉长到长边的长度，就可以画出一个圆了。此外我们将resolution设置为60，这样就能画出更多的三角形，而三角形的个数越多，标识这个圆越接近一个完美的圆形。（事实上是我们不可能画出完美的圆形，只要接近它就可以了。）

const radius: number = 0.5, resolution: number = 60;
const count = resolution + 2;
//将夹角转换成弧度
    const radiation = (Math.PI / 180) * (360 / resolution),
        //中心位置
        center = [0.0, 0.0];
    let vertexs: number[] = center;
    let color: number[] = [0.0, 0.0, 1.0];
    for (let index = 0; index <= resolution; index++) {
        let x = Math.sin(radiation * index) * radius;
        let y = Math.cos(radiation * index) * radius;
        vertexs.push(x);
        vertexs.push(y);
        color.push(0.0, 0.0, 1.0);
    }
...
webgl.drawArrays(webgl.TRIANGLE_FAN, 0, count);

立体模型-3D

在绘制完各种二维图形之后，我们开始来绘制三维图形，这也是webgl的主要作用——构建三维的世界。构建三维立体模型与构建二维图形本质上并没有什么差别，只是我们在绘制三维图形时多了一个深度z，这个值标识了对象在深度上的信息。然后剩下的也和二维图形一样进行三角形的拼接组装。只不过在三维图形里面，拼接三维图形需要使用更多的技巧以及一点点的额外的工作计算。此外，在绘制三维图形时，我们开始使用drawElements替代drawArrays，前者需要传入顶点索引缓存，当然你也可以继续使用drawArrays，究竟使用哪种方式我个人认为需要根据以下条件决定。

内存使用大小，使用drawElements会带来额外的索引字节存储空间，但是使用drawArrays则需要更多的顶点字节存储空间。所以你需要综合考量。
方法的灵活性。就我而言使用drawElements更能帮助我任性定位顶点索引，不会因为某些混乱的判断而画错图形。简单来说drawElements在绘制三维图形时根据有灵活性。
自己的习惯。在充分考虑前面两个因素后，你最后只需要决定你喜欢的方式来绘制即可，根据自己的习惯也能介绍你的开发时间。
立方体
立方体是我们画出的第一个三维图形。立方体的绘制方式也有多种，我们根据评估来用最省内存大额方式来画出一个立方体。首先立方体有2 * 4 个顶点，其次我们按照顺序，在每个顶点链接成不同的三角形，最后画出立方体的每一个面。 ```typescript // v6——- v5 // /| /| // v1———v0| // | | | | // | |v7—-|-|v4 // |/ |/ // v2———v3

const vertex = new Float32Array([ -0.5, -0.5, 0.5, -0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, -0.5, 0.5,

    -0.5, -0.5, -0.5,
    -0.5, 0.5, -0.5,
    0.5, 0.5, -0.5,
    0.5, -0.5, -0.5,

]);

const pointer = new Uint16Array([ 0, 1, 2, 2, 0, 3, // FRONT, 0, 4, 1, 1, 4, 5, // LEFT 2, 3, 7, 2, 7, 6, // RIGHT 4, 5, 6, 4, 6, 7, // BACK 4, 0, 7, 0, 7, 3, // BOTTOM 1, 5, 6, 1, 6, 2 // TOP ]); … webgl.drawElements(webgl.TRIANGLES, count, webgl.UNSIGNED_SHORT, 0);

> 在绘制体的时候我强烈建议你在白纸上先画出坐标和草稿图，立方体是最基础的三维模型，它的顶点非常少，并不会耽误你太多的时间。这样做对培养你的三维知觉能力有帮助。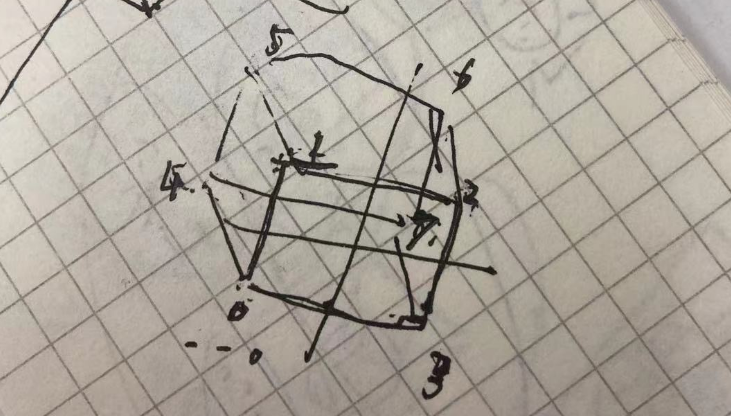
![cube.png](https://cdn.nlark.com/yuque/0/2021/png/2828117/1620905352813-a05ec5a0-672a-4aac-8831-52efce860a62.png#clientId=ue4077aba-225f-4&from=ui&id=u87dde407&margin=%5Bobject%20Object%5D&name=cube.png&originHeight=416&originWidth=731&originalType=binary&ratio=1&size=368706&status=done&style=none&taskId=u4c028df0-2890-447e-a955-2b122bf8305)<br />请诸位原谅我这双狗爪子o(╥﹏╥)o
<a name="z09Tz"></a>
#### 
<a name="CyPMo"></a>
#### 圆锥体
圆锥体实际上有两个面，一个是斜边面，一个是底边面，我们按照同一种绘制方式，求出顶点以及底部圆形的点的位置，就可以绘制出一个圆锥体。
<a name="U5Hqu"></a>
#### 圆柱体
圆柱体的绘制方式类似。不同的是顶部的顶点变成了顶部的一个圆形，相当于我们需要绘制两个圆形，并且将他们连接起来形成侧边。我们首先要画出来的是上下两个圆，圆形绘制的方法以及在前面讲过了圆柱体：
```typescript
const HEIGHT = height,
        TOP = [0, HEIGHT, 0],
        RESOLUTION = 50,
        BOTTOM = [0, -1, 0],
        theta = ((360 / RESOLUTION) * Math.PI) / 180;
    let vertexs: number[] = [];
// 分别计算出上下表面圆边上的点
    for (let index = 0; index < RESOLUTION; index++) {
        // top circle
        const x = Math.cos(theta * index) * radiusB;
        const z = Math.sin(theta * index) * radiusB;
        // bottom circle
        const x1 = Math.cos(theta * index) * radiusT;
        const z1 = Math.sin(theta * index) * radiusT;
        // 上面的圆点每一隔得y轴高度都是统一的，同理，下表面的的圆的y轴也是固定的。
        vertexs.push(x, HEIGHT, z, x1, -1, z1);
    }
    // 其他点1~resolution 底部中心点的位置 resolution + 1; 顶点位置 resolution，
    vertexs.push(...BOTTOM, ...TOP);

现在我们已经把顶点求出来，他们的顺序是这样的一种关系[（顶圆顶点）,（底圆顶点），（顶圆顶点），（底圆顶点），…（底部中心顶点），（顶部中心顶点）]，每一组的顶圆顶点和底圆顶点都在X和Z轴是一致的。现在我们在绘制立方体三维图形的时候使用drawElements方法来给三角形排列。

let pointer: number[] = [];
//斜边
for (let index = 0; index < RESOLUTION * 2; index++) {
  pointer.push(index); // 顶部点的位；
  /* 通过 % 实现当Y Z大于resultion的时候取绝对值，实现点位的循环。
        如：x =40 时 x 为 0  或者x = 41时，x 为 1；
        因为矩形的最后一个三角面点需要和第一个点和第二个点进行合并。
        */
  pointer.push((index + 1) % (RESOLUTION * 2), (index + 2) % (RESOLUTION * 2));
}
//底边
for (let index = 0; index < RESOLUTION; index++) {
  const step = (2 * index + 1) % (2 * RESOLUTION);
  const step2 = (2 * (index + 1) + 1) % (2 * RESOLUTION);
  // 永远是底部中心点开始的
  pointer.push(step);
  pointer.push(RESOLUTION + 1); // 顶部中心点的在vertexs中的位置 即 1 + RESOLUTION
  pointer.push(step2);
}
//顶边
for (let index = 0; index < RESOLUTION; index++) {
  const step = (2 * index + 2) % (2 * RESOLUTION);
  const step2 = (2 * (index + 2)) % (2 * RESOLUTION);
  // 永远是底部中心点开始的
  pointer.push(step);
  pointer.push(RESOLUTION); // 底部中心点的在vertexs中的位置 即 RESOLUTION
  pointer.push(step2);
}
...
webgl.drawElements(webgl.TRIANGLES, pointer.length, webgl.UNSIGNED_SHORT, 0);

我们绘制的方式是，在斜边上绘制三角形，然后绘制上表面和下表面两个圆形（已经讲过，不再重复），斜边的绘制思路未：组成斜边三角形的点分别为（上边圆顶点v1）, 对应的（下边圆顶点v2），最后是（上边圆的接下一个点v3）。请看下图的示意：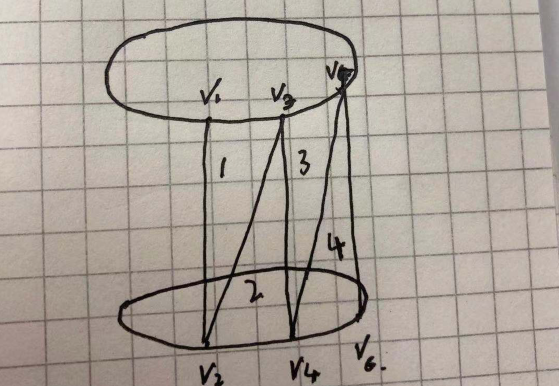

最后我们需要把最后的点和第一个点衔接上，所以使用了取余数%的方式，来判断是否已经经过了一个轮回。这样我们就实现了一个矩形的绘制了。

球体

球体的面积需要我们理解一些数学公式和一定的集合空间观察才能较好的画出来，当然这些公式都是初中书序的知识，非常简单，如果你会正弦、余弦这些概念，那么知道如何画一个球形了。为了搞明白我们来看球体的示意图：

我们需要计算的就是A的距离，因为半径和分割角度都是我们自己定义的，那么只需要通过公式，我们就可以把A点的x，y，z的左边计算出来。（上图的Y 在实际中应该是Z，Z轴则是Y轴）

const RADIUS = radius, RESOLUTION = resolution;
const theta = (180 / RESOLUTION) * (Math.PI / 180);
const beta = (360 / RESOLUTION) * (Math.PI / 180);
//计算出圆体以及表面线条的各个点的位置
let vertexs:number[] = [];
for (let index = 0; index <= RESOLUTION; index++) {
         // 同等高度的Y值 O1-O2
        const y = Math.cos(theta * index) * RADIUS;
        // 底边作为斜边的长度 O2-A
        const d = Math.sin(theta * index) * RADIUS;
        for (let index1 = 0; index1 <= RESOLUTION; index1++) {
            // 斜边的余弦即是x轴的距离 O1-c
            const x = Math.cos(beta * index1) * d;
            // 斜边的正弦即是Z轴的距离 B-C
            const z = Math.sin(beta * index1) * d;
            vertexs.push(x, y, z);
        }
     }

计算出顶点之后，我们再来计算三角形平面的索引。球体可以看成是被很多三角形围成的一个立方体，每个三角形对应的点的计算类似于圆柱体斜边的计算，区别就是圆柱形只需要计算一条区间的三角形数量，而球体需要计算多条区间（多条纬度）的三角形数量：

    /* 计算出顶点的位置为 [0, 1,..... 一个循环之后, RESOLUTION, RESOLUTION + 1]
     我们需要连接的是 0, 1, RESOLUTION 顶点的位置拼凑成一个三角形
    */
    for(var index = 0; index < Math.pow(RESOLUTION, 2); index ++)
    {
            pointer.push(index); // 本行第一个
            pointer.push(index + RESOLUTION + 1); // 下一行第一个
            pointer.push(index + 1); // 本行第二个
            pointer.push(index + 1); // 本行第二个
            pointer.push(index + RESOLUTION + 1); // 下一行第一个
            pointer.push(index + RESOLUTION + 2); // 下一行第二个
            //到此，一个四边形被拼凑成功
    }
 webgl.drawElements(webgl.TRIANGLES, pointer.length, webgl.UNSIGNED_SHORT, 0);

复杂多面体

我们已经绘制完了基本的三维图形，接下来我们要来开始进阶了，开始绘制较为复杂的三维模型。复杂的图形的其中一个难点就是不规则。也就是无法利用简单的数学公式来进行计算顶点的位置了。我们需要更多的、更复杂的数学公式来帮助我们继续深入三维世界。

模型绘制

开篇

基础图元

点

线

三角形

平面图形-2D

矩形

五角星

窗格

圆形

立体模型-3D

立方体

球体

复杂多面体

一支保龄球

一张人脸

总结