代码实现

这个代码是根据书上的描述，自己的写的，先贴代码，然后根据题目的问题逐步分析和拓展该问题。

#include <bits/stdc++.h>
using namespace std;
int primeNumber(int arr[],int n){
    int B[n]={0};
    int point=0;
    for(int i=0;i<n;i+=2){
        if(i+1>n){//数组越界判断
            break;
        }
        if(i==n-1||arr[i]==arr[i+1]){//先判断 i是否等于 n-1，避免 arr[i+1]的访问错误
            B[point++]=arr[i];    
        }
    }
    if(point>=2)//如果有两个，继续递归
        return primeNumber(B,point);
    else if(point==1){//如果有一个，直接返回
        return B[0];
    }else{//如果没有主要元素，返回-1
        return -1;
    }
}
int main()
{
    //int arr[]={3,3,4,2,4,4,2,4,4};
    //int n=9;
    //int arr[]={3,3,4,2,4,4,2,4};
    //int n=8; 
    int arr[]={4,5,6,4};
    int n=4;
    cout<<primeNumber(arr,n)<<endl;
}

注：为了保证一致性，一定要保证arr和B数组的主要元素相同。

a 问

递归是根据生产的数组B的大小来判断是否终止的，具体可见代码。

b 问

当N是奇数时，
代码中的做法，是将最后一个元素单独放入B数组中。
原因如下：
考虑极端情况（特殊情况），在一个数组中，若主要元素是2，将该数组两两分隔（除最后一个元素），形成如下形式：
|2,x1|2,x2|2,x3|2,x4|2,x5|2 ,在生成B数组时候，如果不讲最后一个元素单独放入B数组，则B数组中就遗失了主要元素2。
当然如果2的“聚合度”更高，出现了|2,2|的情况，则不会遗失主要元素。

C 问

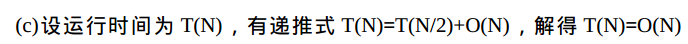
推导过程如下：
T(n) = T(n/2) + O(n)

D 问

B数组直接覆盖写入arr数组。

如何理解保存一个数组A的拷贝？存疑。

E 问

见代码实现。

拓展

其他还有许多的方法，有快有慢。

1. 排序

将数组排序，则arr[n/2]（向下取整）则为主要元素。
时间复杂度和空间复杂度等同于排序算法。

2. 设置 HashMap

统计每种数字出现的次数，找到大于 n/2的那个数并返回。
时间复杂度O（n），空间复杂度O（n）。
参考：找出数组中的主要元素(leetcode169)

3. Moore’s voting algorithm/Boyer-Moore Algorithm

多路投票算法。
分析：时间复杂度为 O（n），空间复杂度O（1），和最开始的代码实现一致，但是该方法无递归，效率更高。
分析参考：
具体参考:多数投票算法(Boyer-Moore Algorithm)详解
主要思想：找出数组中的主要元素(leetcode169)
考虑到存在主要元素的数组，当削减一个非主要元素和一个主要元素后，该数组的主要元素保持不变。
当非主要元素计数时，一定会被主要元素或其他元素削减为0.
当主要元素计数时，可能count会为0，但是主要元素保持不变，相当于削减了问题的规模。否则主要元素会在candidate的位置保持到最后。