一、平衡符号

1. 算法的描述如下：

对应一个字符串，顺序读取，如果是开放符号，则将其推入栈中。如果是封闭符号，且栈空时报错。否则，将栈元素弹出。如果弹出的符号不是对应的开放符号，则报错。在文件尾，如果栈非空则报错。

2. 分析

该算法是在线的（on-line），非常快。

3. 代码实现

可以使用 leetcode 20. 有效的括号 作为题目。

  1. class Solution {
  2. public:
  3.     bool isValid(string s) {
  4.         stack<char> st;
  5.         int length=s.size();
  6.         for(int i=0;i<length;i++){
  7.             if(s[i]=='('||s[i]=='['||s[i]=='{'){
  8.                 st.push(s[i]);
  9.             }
  10.             else if(s[i]==')'||s[i]==']'||s[i]=='}'){
  11.                 if(st.empty()){
  12.                     return false;
  13.                 }
  14.                 char ch=st.top();
  15.                 if(ch=='('&&s[i]==')'||(ch=='['&&s[i]==']')||ch=='{'&&s[i]=='}'){
  16.                     st.pop();
  17.                 }else{
  18.                     return false;
  19.                 }
  20.             }
  21.         }
  22.         return st.empty();
  23.     }
  24. };

LeetCode刷题—20.有效的括号（简单） # 这个博主的讲解非常详细，值得推荐的博客

二、中缀表达式和后缀表达式

1. 后缀表达式

我们平时使用的算式，比如1+23是中缀（infix）表达式，其求解涉及到符号优先级的处理。
我们可以将其写成后缀（postfix）表达式的形式，如此，就可以*避免符号优先级的处理，仅仅使用一个通用的方式去求解算式。

  • 比如：

1+23的后缀表达式形式：123+

  • 求解方法如下：

见到后缀表达式的一个数，就将其压入栈中，遇到符号就将其作用于栈弹出的两个数上，并将结果压入栈中。
题目可以见 ：150：逆波兰求值。
代码如下：

  1. class Solution {
  2. public:
  3.     int evalRPN(vector<string>& tokens) {
  4.         if(tokens.empty()){
  5.             return 0;
  6.         }
  7.         stack<int> st;
  8.         int size=tokens.size();
  9.         for(int i=0;i<size;i++){
  10.             if(tokens[i]=="+"){
  11.                 int t1=st.top();st.pop();
  12.                 int t2=st.top();st.pop();
  13.                 st.push(t1+t2);
  14.             }
  15.             else if(tokens[i]=="-"){
  16.                 int t1=st.top();st.pop();
  17.                 int t2=st.top();st.pop();
  18.                 st.push(t2-t1);
  19.             }
  20.             else if(tokens[i]=="*"){
  21.                 int t1=st.top();st.pop();
  22.                 int t2=st.top();st.pop();
  23.                 st.push(t1*t2);
  24.             }
  25.             else if(tokens[i]=="/"){
  26.                 int t1=st.top();st.pop();
  27.                 int t2=st.top();st.pop();
  28.                 st.push((int)t2/t1);
  29.             }else{
  30.                 int number=atoi(tokens[i].c_str());
  31.                 st.push(number);
  32.             }
  33.         }
  34.         return st.top();
  35.     }
  36. };

关于这一题我踩了一些坑。

string 转int

int number=atoi(tokens[i].c_str());
其中string方法 c_str 函数返回一个 c字符串指针，内容与string 相同。
atoi可以将c字符串转换为数字。（如果字符串不是数字，则返回0）

关于除法的取整

这里，中文题目描述的不是很清楚，英文版的题目是 truncate to zero，也就是取整要向数轴的0靠近，
这里采用的是 直接浮点数的强制转换即可达到目的。
C++的取整：向下取整，向上取整，四舍五入取整，直接去小数点取整 #更多的取整函数和方式

stack 的类型

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. int main()
  4. {
  5.     stack<char> s;
  6.     stack<int> st;
  7.     s.push(12); # 存储的是ascii 中的12号符号
  8.     # 注意：此时如果压入栈的是负数，则程序出错，打印不出来值。
  9.     st.push(12); #存储的是整数
  10.     cout<<s.top()<<" "<<st.top()<<endl;
  11. }

2. 中缀表达式转换成后缀表达式

中缀表达式可以包含括号。
弹出规则，在处理符号a时，依此弹出所有的比a优先级高或相等的符号，最后再将a压入栈中。
例子和步骤见下图：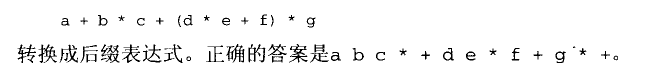
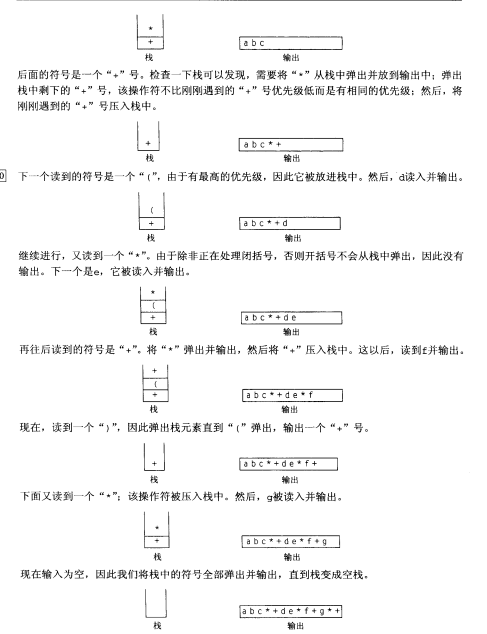
image.png
image.png
image.png
括号的情况比较特殊，现说明如下：
一句话，左括号在处理的时候入栈，在处理右括号的时候出栈。

  • 左括号

当左括号输入的时候，有最高的优先级，从而保证其不会删除其他运算符。
已经在栈中的时候，左括号被看成最低优先级，进而不会被其他运算符删除。【理解即可，不需要硬记】

  • 右括号

只有在处理右括号的时候，才能弹出左括号。此时左括号只被弹出并不输出，右括号也是如此。

反思

以上的操作默认情况下，都是从左向右结合的，也就是说ab-c-被理解为a-b-c。
有些情况下，符号可以从右向左结合，比如2^2^3=2^8=256,而不是4^3=64.【待做，习题】

3. 拓展

[LeetCode] Basic Calculator 基本计算器（未完成）
这题是有难度的，注意要更加灵活的运用模型【不需要使用后缀表达式的优点：统一优先级】。

三、函数调用-尾递归

尾递归为啥能优化？ # 讲的非常详细

  • 背景

在递归调用时，在跳转到子函数时，需要将主函数的一些变量和入口地址存储起来。
在函数返回时，则查看保存的变量和入口地址，将主函数复原。

  • 实现的方法

用栈来实现这个过程，但是随着递归层数的深入，栈空间可能溢出。
有可能是因为递归基的非正常工作，或者递归程序本身就需要这么多空间。
其中，有一种递归情况，叫做尾递归，可能出现第二种情况，且完全可以不用这么多空间（可以优化）。

1. 例子

  • 尾递归

    1. function fact(n, r) {
    2.   if (n <= 0) {
    3.       return 1 * r;
    4.   } else {
    5.       return fact(n - 1, r * n);
    6.   }
    7. }

    此时，父函数的所有变量对最终结果没什么贡献。所以并不需要栈来进行多层的记录。

  • 不是尾递归

    1. function fact(n) {
    2.   if (n <= 0) {
    3.       return 1;
    4.   } else {
    5.       return n * fact(n - 1);
    6.   }
    7. }

    而上图的情况就有必要记录父函数的变量了，这种情况不是尾递归。

    2. 编译器自动优化尾递归

    image.png
    image.png
    虽然尾递归的去除很简单，有些编译器可以自动的完成，但是还是需要在自己的代码中避免。

    3. 总结

    本质上，递归总是可以去除的，转换成迭代【没有试过】（编译器在转变成编译语言的时候完成的）（使用栈来完成）。
    但是递归转迭代牺牲了可读性，但是提高了速度。