堆、二叉堆

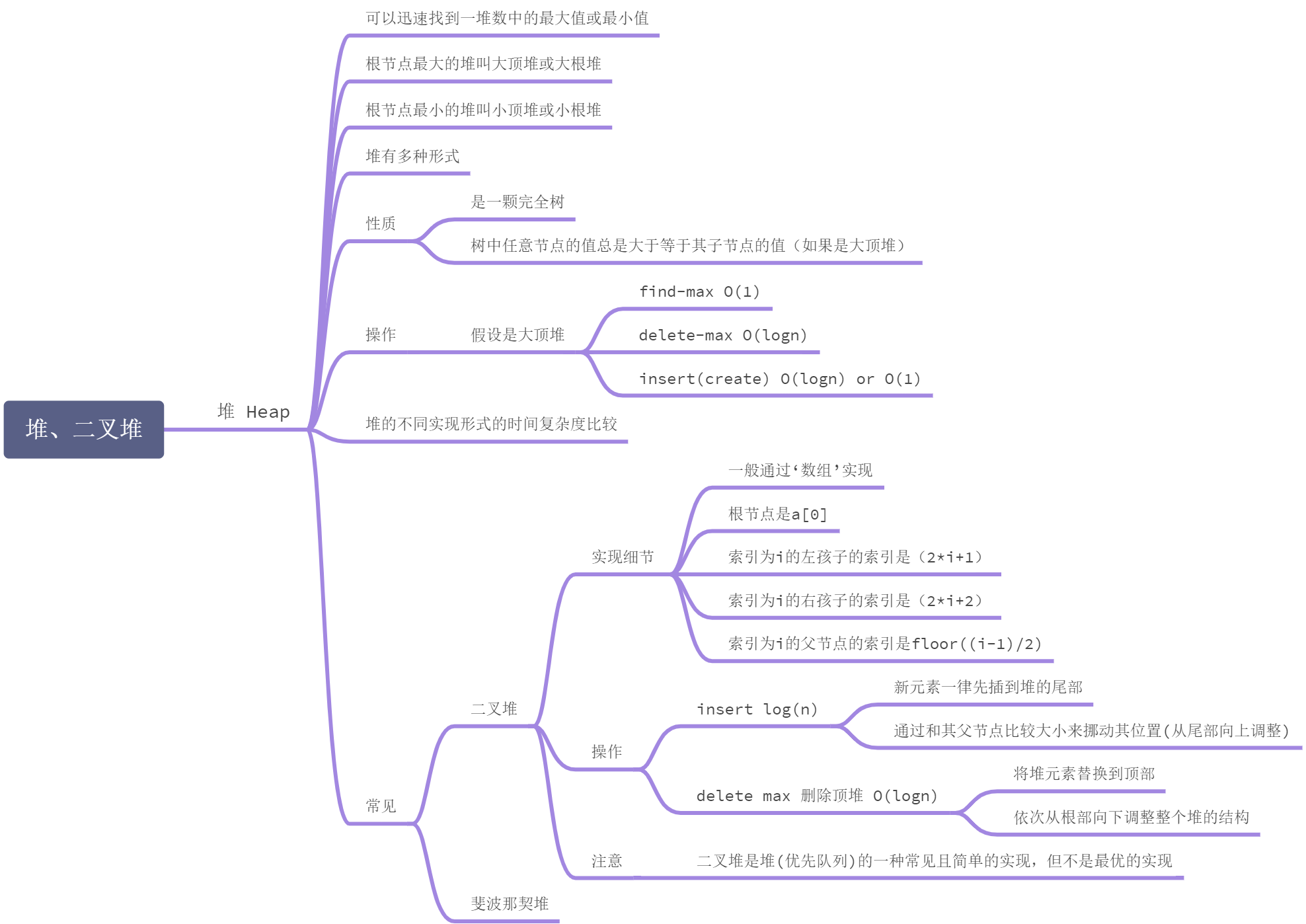
二叉堆

实现

二叉堆通过数组实现，假设第一个元素在数组中的索引为零的话：

1. 索引为 i 的左孩子的索引是 （2*i+1）
2. 索引为 i 的右孩子的索引是 （2*i+2）
3. 索引为 i 的父节点的索引是 floor((i-1)/2)

将从根节点开始依次从左到右放入每一个节点的值：
可以看到满足堆的性质，是一颗完全树（除叶子节点外其他节点都是满的），而且根节点一定大于儿子节点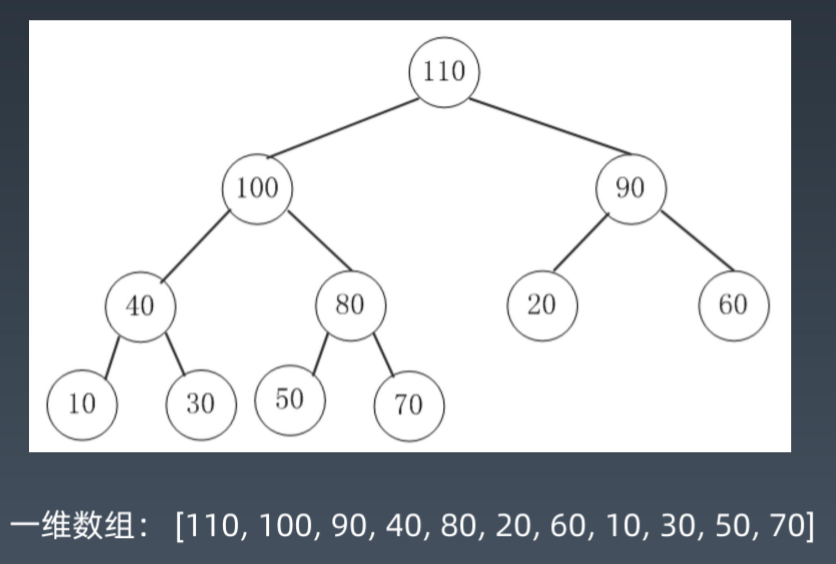

实现代码

// Java
import java.util.Arrays;
import java.util.NoSuchElementException;
public class BinaryHeap {
    //这个d表示二叉树，如果想要三叉树、多叉树可以改变d的值
    private static final int d = 2;
    private int[] heap;
    private int heapSize;
    /**
     * This will initialize our heap with default size.
     */
    public BinaryHeap(int capacity) {
        heapSize = 0;
        heap = new int[capacity + 1];
        Arrays.fill(heap, -1);
    }
    public boolean isEmpty() {
        return heapSize == 0;
    }
    public boolean isFull() {
        return heapSize == heap.length;
    }
    private int parent(int i) {
        return (i - 1) / d;
    }
    /**
    * 计算左右孩子的位置
    * i是父亲节点的位置
    * k=1就是左儿子，k=2就是右儿子
    */
    private int kthChild(int i, int k) {
        return d * i + k;
    }
    /**
     * Inserts new element in to heap
     * Complexity: O(log N)
     * As worst case scenario, we need to traverse till the root
     */
    public void insert(int x) {
        if (isFull()) {
            throw new NoSuchElementException("Heap is full, No space to insert new element");
        }
        heap[heapSize] = x;
        heapSize ++;
        heapifyUp(heapSize - 1);
    }
    /**
     * Deletes element at index x
     * Complexity: O(log N)
     */
    public int delete(int x) {
        if (isEmpty()) {
            throw new NoSuchElementException("Heap is empty, No element to delete");
        }
        int maxElement = heap[x];
        heap[x] = heap[heapSize - 1];
        heapSize--;
        heapifyDown(x);
        return maxElement;
    }
    /**
     * Maintains the heap property while inserting an element.
     */
    private void heapifyUp(int i) {
        int insertValue = heap[i];
        while (i > 0 && insertValue > heap[parent(i)]) {
            heap[i] = heap[parent(i)];
            i = parent(i);
        }
        heap[i] = insertValue;
    }
    /**
     * Maintains the heap property while deleting an element.
     */
    private void heapifyDown(int i) {
        int child;
        int temp = heap[i];
        while (kthChild(i, 1) < heapSize) {
            child = maxChild(i);
            if (temp >= heap[child]) {
                break;
            }
            heap[i] = heap[child];
            i = child;
        }
        heap[i] = temp;
    }
    private int maxChild(int i) {
        int leftChild = kthChild(i, 1);
        int rightChild = kthChild(i, 2);
        return heap[leftChild] > heap[rightChild] ? leftChild : rightChild;
    }
    /**
     * Prints all elements of the heap
     */
    public void printHeap() {
        System.out.print("nHeap = ");
        for (int i = 0; i < heapSize; i++)
            System.out.print(heap[i] + " ");
        System.out.println();
    }
    /**
     * This method returns the max element of the heap.
     * complexity: O(1)
     */
    public int findMax() {
        if (isEmpty())
            throw new NoSuchElementException("Heap is empty.");
        return heap[0];
    }
    public static void main(String[] args) {
        BinaryHeap maxHeap = new BinaryHeap(10);
        maxHeap.insert(10);
        maxHeap.insert(4);
        maxHeap.insert(9);
        maxHeap.insert(1);
        maxHeap.insert(7);
        maxHeap.insert(5);
        maxHeap.insert(3);
        maxHeap.printHeap();
        maxHeap.delete(5);
        maxHeap.printHeap();
        maxHeap.delete(2);
        maxHeap.printHeap();
    }
}

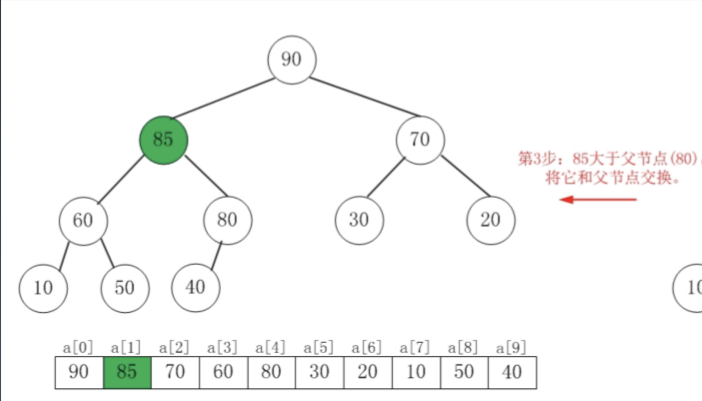
Insert 的实现细节

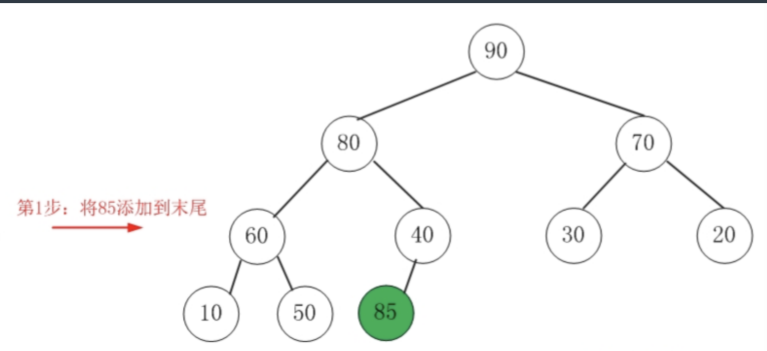
1. 新元素一律先插到堆的尾部
2. 依次向上调整整个堆的结构（一直到根即可）

如果要把85插到二叉堆中：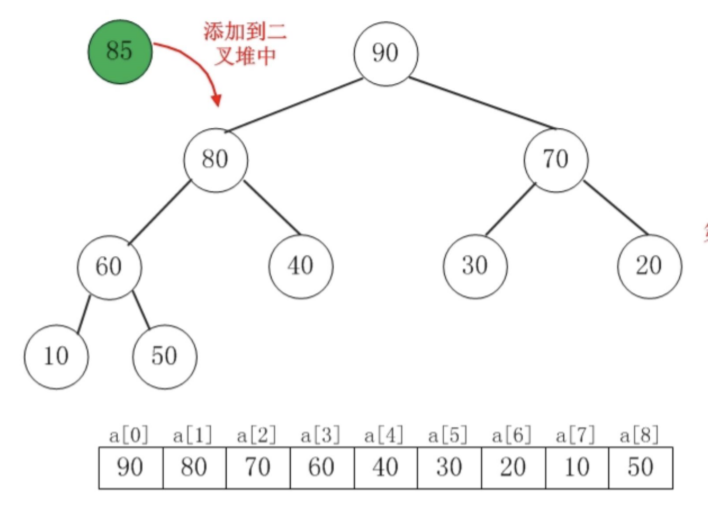

核心代码

public void insert(int x) {
        if (isFull()) {
            throw new NoSuchElementException("Heap is full, No space to insert new element");
        }
        heap[heapSize] = x;
        heapSize ++;
        heapifyUp(heapSize - 1);
    }
    /**
     * Maintains the heap property while inserting an element.
     */
    private void heapifyUp(int i) {
        int insertValue = heap[i];
        while (i > 0 && insertValue > heap[parent(i)]) {
            heap[i] = heap[parent(i)];
            i = parent(i);
        }
        heap[i] = insertValue;
    }

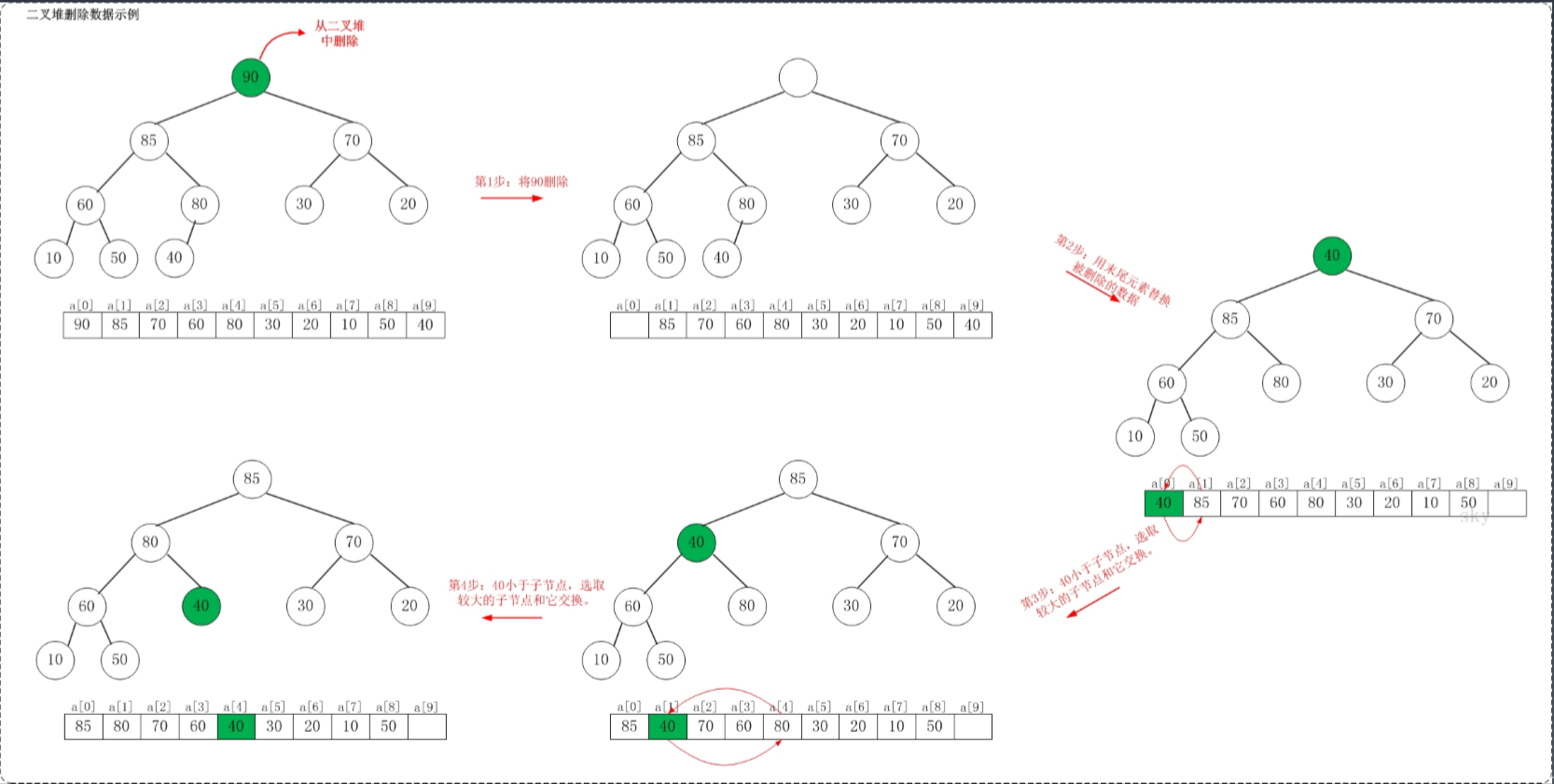
Delete Max 的实现细节

1. 将堆尾元素替换到顶部
2. 依次从根部向下调整整个堆的结构(一直到堆尾即可)

核心代码

    /**
     * Deletes element at index x
     * Complexity: O(log N)
     */
    public int delete(int x) {
        if (isEmpty()) {
            throw new NoSuchElementException("Heap is empty, No element to delete");
        }
        int maxElement = heap[x];
        heap[x] = heap[heapSize - 1];
        heapSize--;
        heapifyDown(x);
        return maxElement;
    }
    /**
     * Maintains the heap property while deleting an element.
     */
    private void heapifyDown(int i) {
        int child;
        int temp = heap[i];
        while (kthChild(i, 1) < heapSize) {
            child = maxChild(i);
            if (temp >= heap[child]) {
                break;
            }
            heap[i] = heap[child];
            i = child;
        }
        heap[i] = temp;
    }