Dynamic Programming

关键点

  1. 动态规划 和 递归或者分治没有本质上的区别 （关键看有无最优的子结构）
  2. 共性 ：找到重复子问题

  3. 差异性：最优子结构、中途可以淘汰次优解

    DP的步骤

  4. 找重复性（分治）

  5. 定义状态数组

  6. DP方程

    DP例题解析

    Fibonacci数列

  7. 斐波那契数列如果用傻递归的话，因为有很多的重复计算，时间复杂度就是指数级的，如下

    1. int fib(int n) {
    2.  if (n <= 1) {
    3.     return n;
    4.  }
    5.  return fib(n - 1) + fib(n - 2);
    6. }

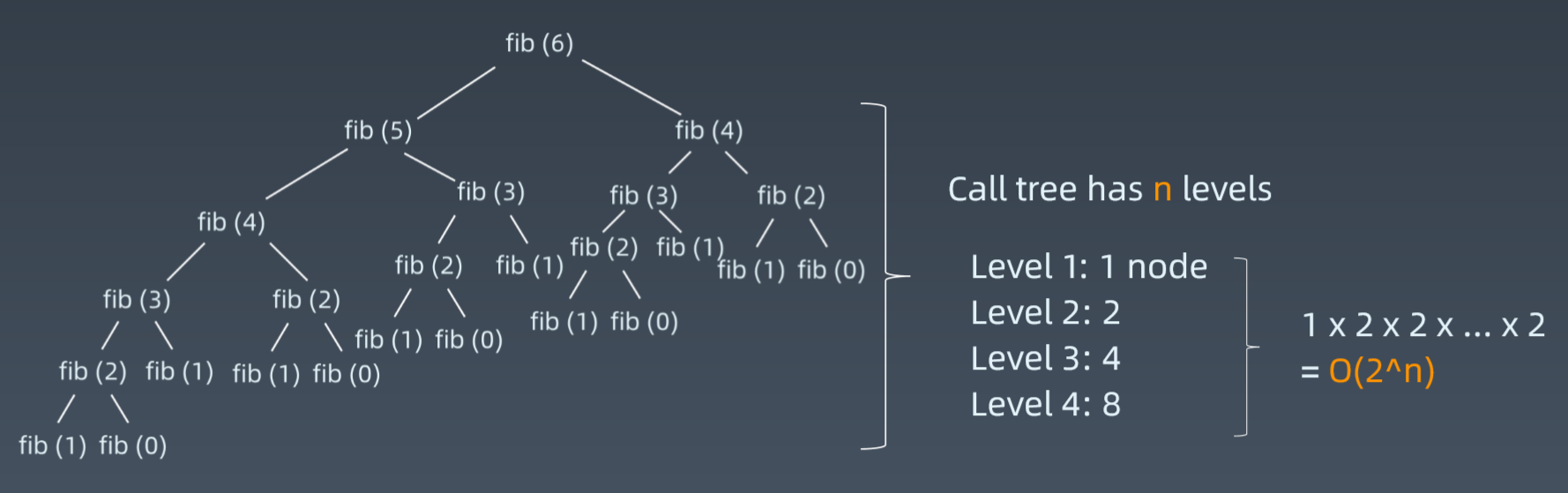
    image.png
    简化代码：简化速度以及简化表达。
    以下是简化表达，使用三元表达式

    1. int fib(int n) {
    3.  return n <= 1 ? n : fib(n - 1) + fib(n - 2);
    4. }

  8. 递归的时候加一个缓存（记忆化搜索），可以加一个数组来存放已经计算出来的值，下次使用的时候就不用重复计算了，直接在缓存中拿，这样时间复杂度就降到了O(n)

    1. int fib(int n , int[] memo) {
    2.  //递归终止条件
    3.  if (n <= 1) {
    4.     return n;
    5.  }
    6.  //因为Fibonacci数列都是正数，等于0说明这个值没有被计算过
    7.  if (memo[n] == 0){
    8.      memo[n] = fib(n - 1) + fib(n - 2);
    9.  }
    10.  return memo[n];
    11. }

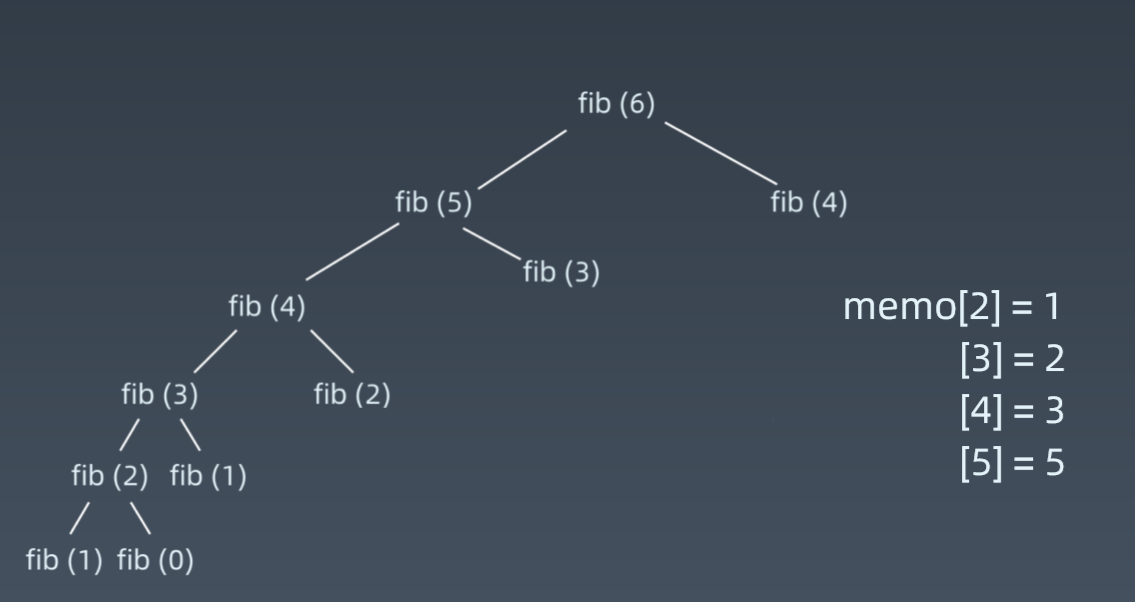
    image.png

  9. DP - 直接写一个循环，自底向上递推，不断累加。（递归的思维是自顶向下）

F[n] = F[n - 1] + F[n - 2] 

  1. int fib(int n , int[] a) {
  2.     a[0] = 0;
  3.     a[1] = 1;
  4.     for (int i = 2;i <= n;i++) {
  5.         a[i] = a[i - 1] + a[i - 2];
  6.     }
  8. }

路径计数

如下图，求从左上角到右下角有多少种不同的走法。绿人只能往下和右两个方向走，橙色部分是障碍物。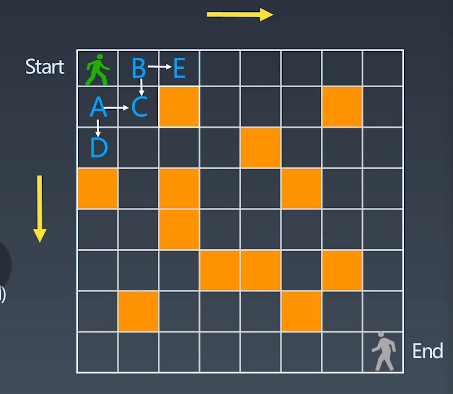
image.png

  1. 递归 - 注意要用计算机的思维，分治找重复的子问题。

解析：
如果想要从 start 走到 end ，绿人一步只能先走到 B 或者先走到 A ，那么就可以分解为子问题了。
子问题1：求从 B 走到 end 有多少种不同的走法；
子问题2：求从 A 走到 end 有多少种不同的走法；
那么子问题1 的解 + 子问题2 的解 就是从左上角到右下角不同的走法的解。
这就是分治的思想，如图：
image.png

  1. int countPaths(boolean[][] grid, int row, int col){
  2.         //如果遇到障碍物返回0
  3.         if (!validSquare(grid, row, col)) {
  4.             return 0
  5.         }
  7.         if (isAtEnd(grid, row, col)) {
  8.             return 1;
  9.         }
  10.         return countPaths(grid, row + 1, col) + countPaths(grid, row, col + 1);
  11.     }
  1. DP - 递推

递推就是自底向上的思想，如下图，到达终点只能从上面的格子和左边的格子走一步。每一个格子的走法都是其上面的格子的走法加上左格子的走法，遇到障碍物就是0.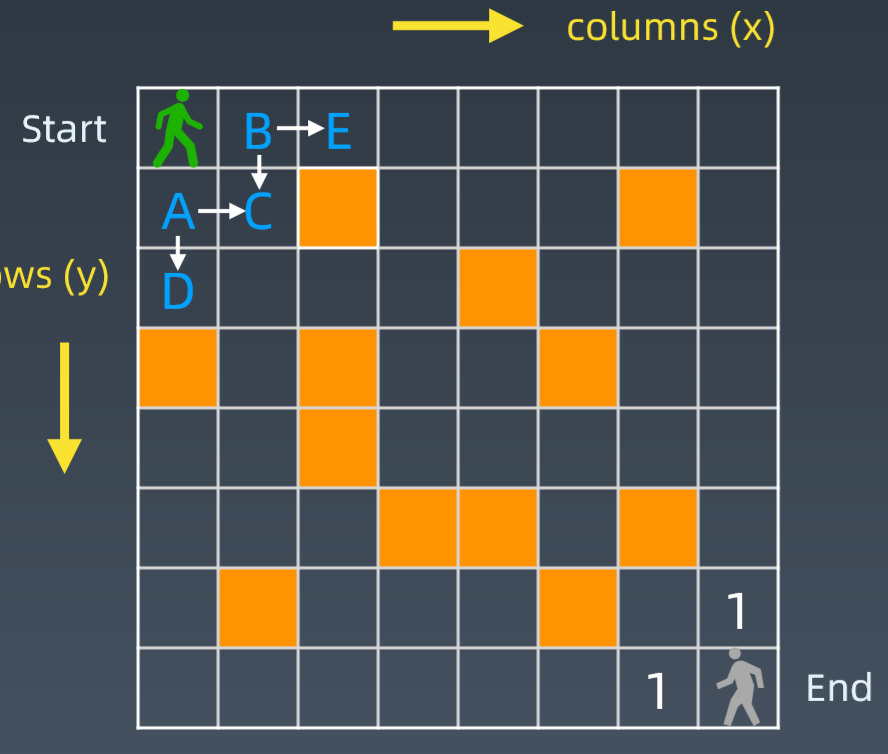
image.png
依次向上递推，我们可以得到一个递推公式，即 opt[i , j] = opt[i, j + 1] + opt[i+ 1, j] ， [i, j] 表示坐标位置。
完整逻辑：

  1. if opt[i, j] = "空地"
  2.     opt[i, j] = opt[i, j + 1]  + opt[i + 1, j];
  3. else
  4.     opt[i, j] = 0;

发现最终的方法总是是 10+17 = 27 。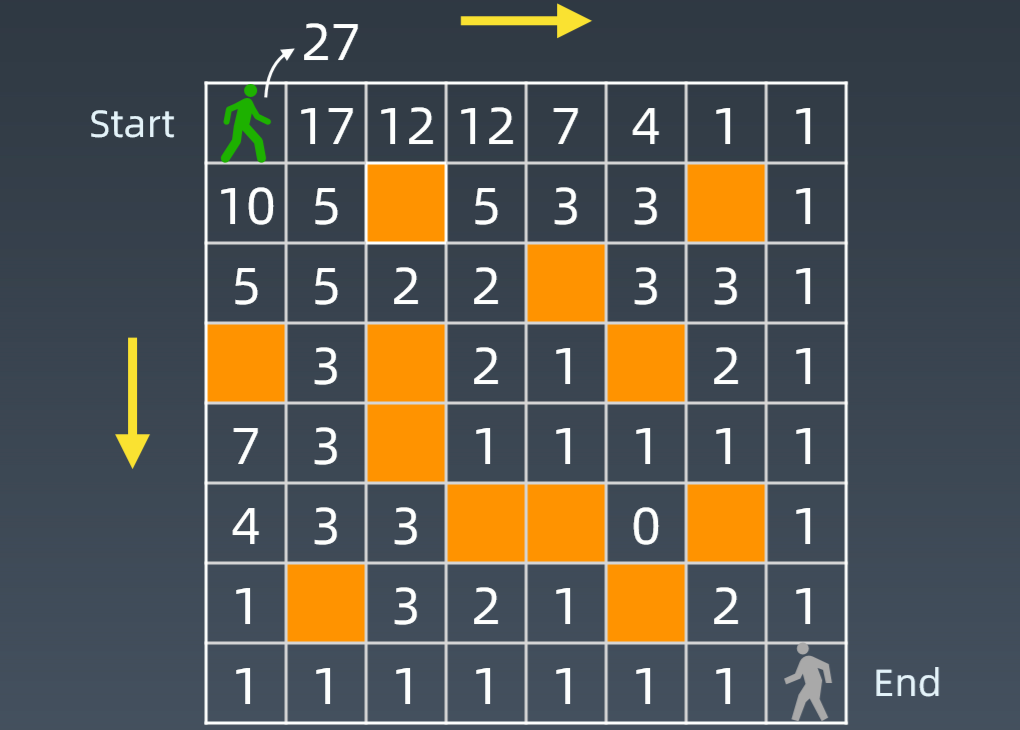
image.png
leetcode题解 不同路径Ⅱ

  1. /*DP
  2. 1. 先分析出DP方程
  3. 2. 确定边界，除障碍物外边界都为1
  4. 3. 使用DP方程不断累加，这里也要注意除去障碍物
  5. */
  6. class Solution {
  7.     public int uniquePathsWithObstacles(int[][] obstacleGrid) {
  8.         //如果入口就有障碍，方法就为0
  9.         if (obstacleGrid[0][0] == 1) {
  10.             return 0;
  11.         }
  12.         int m = obstacleGrid.length;
  13.         int n = obstacleGrid[0].length;
  14.         int[][] dp = new int[m][n];
  15.         for (int i = 0 ; i < m && obstacleGrid[i][0] == 0; i++) {
  16.             dp[i][0] = 1;
  17.         }
  18.         for (int i = 0 ; i < n && obstacleGrid[0][i] == 0; i++) {
  19.             dp[0][i] = 1;
  20.         }
  21.         for (int i = 1; i < m; i++) {
  22.             for (int j = 1;j < n;j++) {
  24.                 if(obstacleGrid[i][j] == 0) {
  25.                     dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
  26.                 }
  27.             }
  28.         }
  29.         return dp[m - 1][n - 1];
  30.     }
  31. }

总结

  1. 最优子结构 opt[n] = best_of(opt[n - 1], opt[n - 2], ...)
  2. 存储中间状态： opt[i]

  3. 递推公式（状态转移方程或DP方程）

    Fib : opt[i] = opt[n - 1] + opt[n - 2]
    二维路径： opt[i,j] = opt[i + 1, j] + opt[i, j + 1] （且判断 a[i,j] 是否空地）