定义

一种在每一步选择中都采取当前状态下最好或最优的选择，从而希望导致结果是全局最好或最优的算法。

区别

  1. 贪心：当前做局部最优判断，不能回退
  2. 回溯：可以回退

  3. 动态规划：会保存以前的最优结果并根据以前的结果对当前做出选择，可以回退

    解释

  4. 贪心法可以解决一些最优化问题，如：求图中的最小生成树、求哈夫曼编码 等，然而对于工程和生活中的问题，贪心法一般不能得到我们所要求的答案。

  5. 一旦一个问题可以通过贪心算法来解决，那贪心法一般是解决此问题的最优解。
  6. 由于其高效性 ，贪心法可以作为辅助算法
  7. 也可由用来解决一些结果要求不是很精准的问题

    例子

    零钱兑换
    此例子为了说明有些特定的情况才能使用贪心算法。
    1. 当硬币可选集合固定：Coins = [20, 10, 5, 1]
    2. 求最少可以几个硬币拼出总数。 比如 total = 36
    如果是像上面特定的问题，那用贪心算法求解是最优的，如下：
    由于20，10，5，1都是可以整除最大的数20的，所以只要按顺序减掉最大的数就可以得出结果。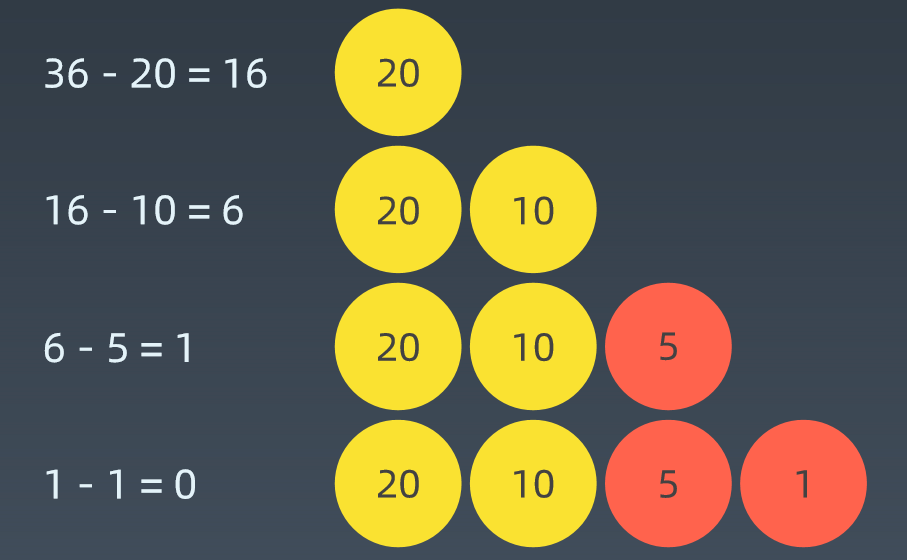
    image.png
    而如果是非整除关系的硬币呢 ``` 可选集合：Coins = [10, 9, 1]

求拼出总数为 18 最少需要几个硬币？ ``` 两个9就可以拼出18了，但是如果用贪心算法，如下：
要用好多硬币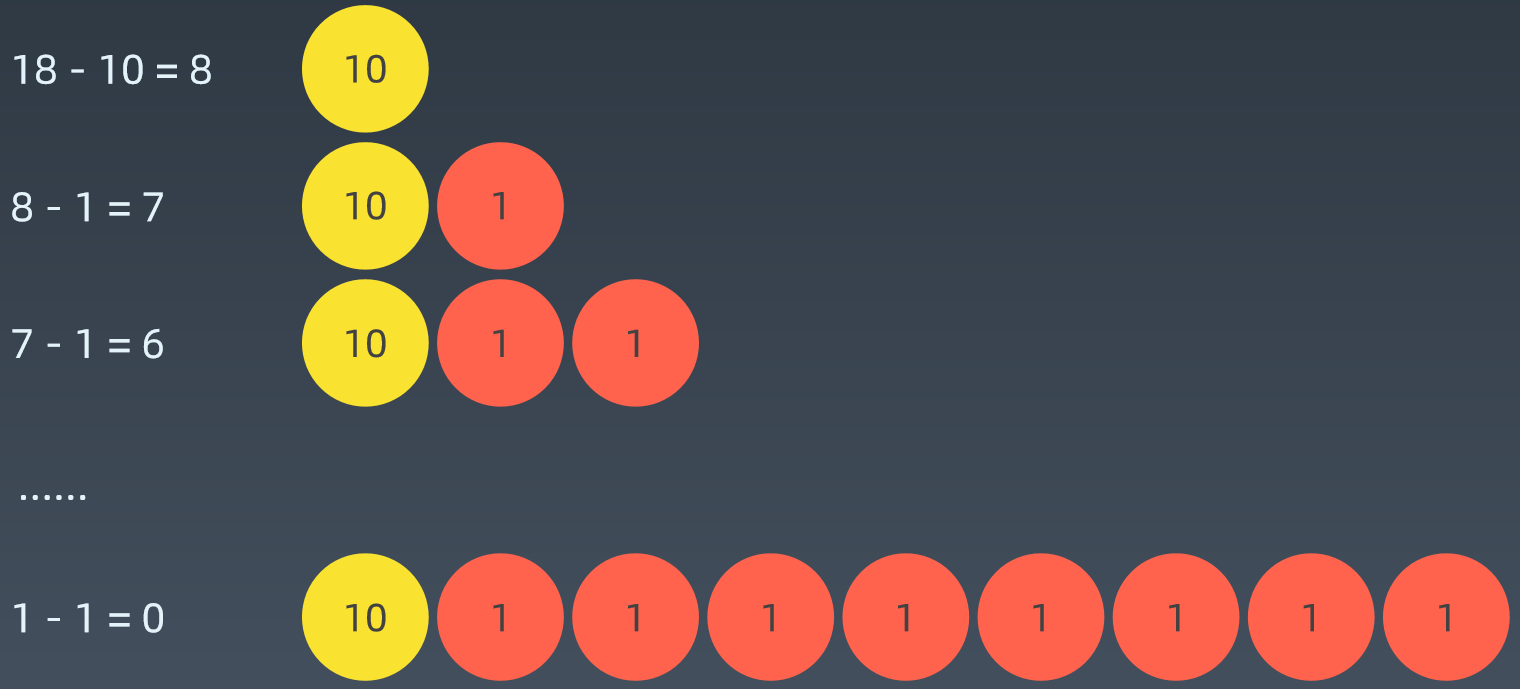
image.png

适用场景

问题能够分解为子问题，且子问题的最优解能够递推到最终问题的最优解。
这种子问题最优解称为最优子结构。