代码：https://github.com/spongezhang/Deep-Transfer-Network/tree/master/code

论文：域适应.pdf

Abstract

域适应旨在在一个数据集中训练分类器并将其应用于相关但不相同的数据集。 一个成功使用的域适应框架是学习一种变换来匹配特征的分布（边际分布）和给定特征的标签分布（条件分布）。 在本文中，我们提出了一种名为深度传输网络（DTN）的新域适应框架，其中高度灵活的深度神经网络用于实现这种分布匹配过程。 这是通过 DTN 中的两种类型的层来实现的：共享特征提取层学习共享特征子空间，其中源样本和目标样本的边缘分布被拉近，判别层通过分类器转换匹配条件分布。 我们还表明，DTN 的计算复杂度与训练样本的数量成线性关系，使其适用于大规模问题。

Introduction

传统的机器学习需要大量的训练样本才能训练出可靠的模型。 然而，在许多实际应用中，获得足够的标记训练数据是昂贵的，有时甚至是不可能的。 一个直接的解决方案是在标记数据集上训练模型，与目标任务相关但不完全相同，并将模型应用于正在考虑的数据。 不幸的是，由于不同的特征和标签分布[5]，模型的性能在域转移期间可能会急剧下降。 为了解决这个问题，旨在从一个数据集（源数据集）学习并将知识转移到相关但不相同的数据集（目标数据集）的领域适应成为一个活跃的研究课题[25]。 这种方法被广泛用于对象分类 [1]、对象检测 [6, 14] 单次学习 [9] 等。

大多数领域适应方法的关键是学习对特征的转换，以减少源数据集和目标数据集之间分布的差异。 现实世界的问题有不同的情况。 1）边际分布不同，而条件分布相似。 2）边际分布相似，而条件分布不同。 3）边际分布和条件分布都是不同的[30]。�

实例重加权 [3, 4] 和子空间学习 [12, 11, 19, 27, 24] 是域适应的两种典型学习策略 [22]。 前者通过重新加权源样本来减少分布差异，并在加权的源样本上训练分类器。 后者试图找到两个数据集的分布匹配的共享特征空间。 还有一些方法同时执行实例重新加权和子空间学习，并在许多基准数据集中实现了最先进的结果 [22�

分类器转导代表了领域适应的另一个独立研究方向 [20]。 它通过将分布适应与模型正则化结合起来直接设计一个自适应分类器[7,23,20]。 一个典型的策略是在优化过程中对条件分布使用一定的正则化。 例如，最小化分类器输出之间的度量可以减少源数据集和目标数据集 [20] 的条件分布的差异，因此可以训练自适应分类器。�

最近，它已经在许多具有挑战性的案例中得到证明，不同领域之间的边际分布和条件分布可能不同。 同时匹配它们可以显着提高最终分类器的性能[30,22,20]。 属于这一类的方法在基准数据集上取得了出色的表现。 然而，它们中的许多具有很高的计算复杂度（[22] 中的 O(n2 ) 和 [20] 中的 O(n3 )）。 它使大规模问题的计算成本高得令人望而却步。�

基于神经网络的深度学习方法在机器学习和模式识别方面取得了许多鼓舞人心的成果[17]。 最近，神经网络已成功用于解决域适应问题，例如情感分类 [10] 和行人检测 [29]。 然而，通过神经网络显式匹配数据集的分布来解决一般领域适应问题的工作很少。 这种显式匹配策略已被证明在最先进的方法中至关重要[30,22,20]。�

在这项工作中，我们提出了深度传输网络 (DTN)，其中使用深度神经网络来建模和匹配边际分布和条件分布。 深度神经网络和领域适应的结合为我们提供了三个独特的优势�

• 神经网络结构使我们的模型适合通过同时匹配边际分布和条件分布来实现域转移。 我们通过 DTN 中的两种不同类型的层来实现这一点：共享特征提取层，它学习一个子空间以匹配源和目标样本的边缘分布，以及通过分类器转换匹配条件分布的判别层（第 2 节） .�
• 与之前的工作相比，本文方法可以在O(n)时间内进行优化，其中n为训练数据点的数量。与其他方法([21,22]中的O(n2)和[20]中的O(n3))相比，该方法更适合处理大规模域适应问题(章节3和4)。�
• 通过结合这两个领域的最佳范例(识别方面的神经网络，以及域适应方面的边缘分布和条件分布匹配)，我们通过大量实验表明，所提出的方法在计算时间和准确性方面优于最先进的方法。为了在大规模设置中展示我们的方法，我们在两个数据集上进行了测试，这两个数据集的大小是广泛使用的Office-Caltech数据集的10倍。令人印象深刻的是，在USPS/MNIST数据集上，DTN实现了28.95%的精度提高(第4节)。�

Deep Transfer Network

Problem Formulation

设为d维列向量。和分别代表源域和目标域数据集。是x的对应标签。给定带标签的源数据集和无标签的目标数据集,其中和是数据点的数量，域适应的目标是要使用所有给定数据最小化目标数据集的预测误差 来学习统计模型，其中是模型第 i 个目标数据点的预测标签，�是相应的真标签，训练中是未知的。我们考虑源数据集和目标数据集的边缘分布和条件分布都不同的情况。�和是边缘分布，而和代表条件分布

Preliminary

在DTN中采用了分布匹配策略。为了匹配分布，需要定义两个分布之间差异的度量。 我们遵循[19]并采用经验最大平均差异（MMD）作为非参数度量。MMD 是两个分布之间差异的常用度量，因为它在计算和优化方面的效率[26。用和分别表示和的数据矩阵。用数据矩阵表示和。源数据集和目标数据集的边缘分布之间的MMD被定义为：

其中M是MMD矩阵，Mij 是M中的元素。 Mij 可以计算为：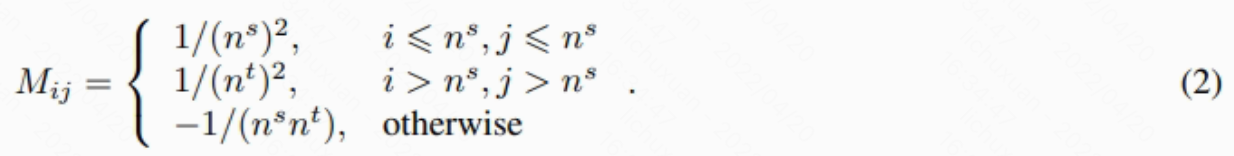

典型神经网络由两种层组成：

• 特征提取层，通过线性投影(或卷积)和非线性激活函数将输入数据投影到另一个空间。
• 判别层，在此进行最终的标签预测。�

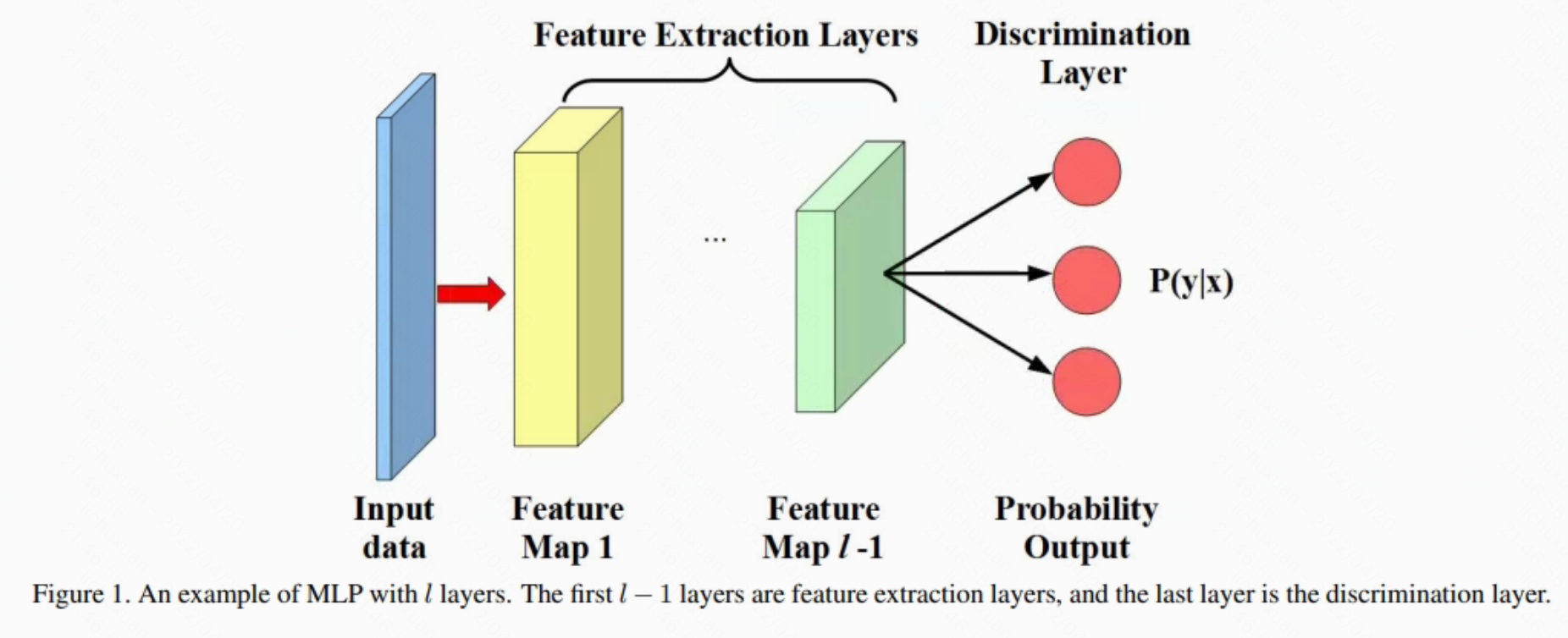
例如，在卷积神经网络 (CNN) 中，特征提取层由卷积层和全连接层组成，判别层由 softmax 回归层组成。 在具有 l 层的多层感知器 (MLP) 中（如图 1 所示），前 l-1 个全连接层是特征提取层，而最后一个 softmax 回归层是判别层。 下面，我们将基于 MLP 开发 DTN。 我们的方法可以很容易地扩展到其他类型的神经网络

�

Matching Marginal Distribution

MLP 定义了一系列函数。 我们首先考虑单层神经网络。 单层神经网络通过线性投影和非线性向量值激活函数 f(·) 将 x 映射到 k 维特征向量 h�。

其中W是 k*d 的投影矩阵。常用的 f(·) 包括 和 。
单层神经网络可以被连接形成深度神经网络，一层的输出可以成为另一层的输入。
对于一个有l层的MLP来说，前l-1层都是特征提取层。设是x在第l-1层的特征。用和表示源数据集和目标数据集的特征分布。我们所提方法的目标是让和接近。这是通过在训练特征映射函数时最小化MMD来实现的�。
用表示源数据集的特征矩阵，表示目标数据集。
是和的组合。和之间的距离由边缘 MMD 建模如下�：

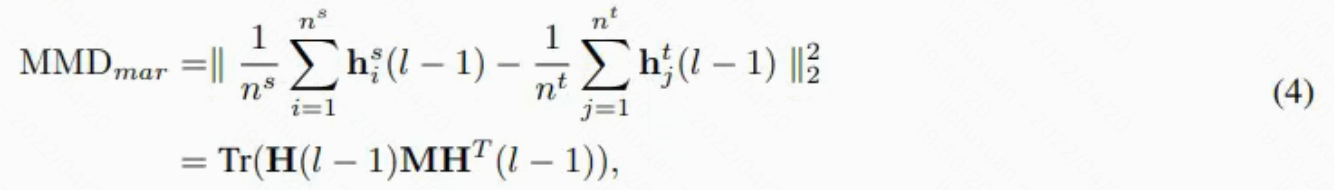
其中M是等式2中定义的MMD矩阵。

Matching Conditional Distributions

在本文中，我们将逻辑回归视为判别层的模型。 它将输入数据点投影到一组超平面，到这些平面的距离反映了后验概率。 假设数据集中共有 C 个类别。 对于任意类别 c，类别 c 的超平面表示为 wc。 给定特征 x 的 y=c 的后验概率可以建模为�：

源数据集和目标数据集的条件分布之间的距离由条件MMD测量，定义为：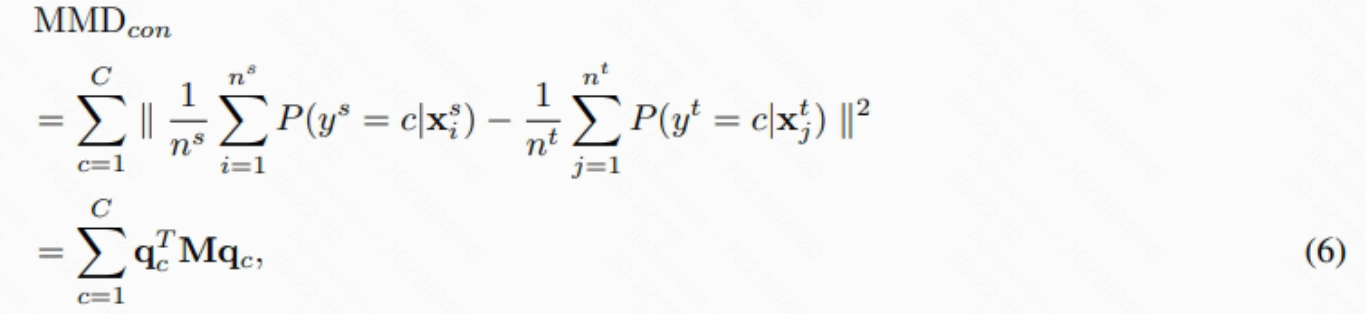

其中是所有数据点的第c类的后验分布输出向量，M是等式2中定义的MMD矩阵。条件MMD越小，源数据集和目标数据集的条件分布越接近。稍后，我们将展示如何最小化上面的内容。�
为了估计目标样本的条件分布，需要给出目标样本的标签。 然而，目标标签在无监督域适应中是未知的。 在这种情况下，可以使用一些基本分类器，例如 SVM、MLP，来获得目标样本的伪标签。 在这项工作中，非迁移神经网络被用作基分类器。 我们迭代更新目标样本的标签以确保良好的性能（过程如第 3 节所示）。 这在经验上提供了良好的性能。�

Final Objective Function

通过使用最后一个特征提取层的输出作为判别层的输入，我们得到了 DTN。 特征提取层找到一个共享子空间，其中源数据集和目标数据集的特征的边缘分布是匹配的。 然后在新的共享特征空间中训练一个自适应分类器以匹配条件分布。 这部分给出了 DTN 的最终目标。�
我们使用负对数似然，这是目标函数中常用的损失函数。 它被定义为�：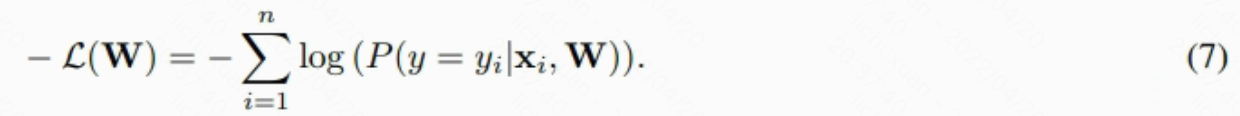

其中 W 是等式 3 中神经网络的投影矩阵。 将 Eq.4 和 Eq.6 整合到 Eq.7 中，我们可以得到 DTN 的最终目标函数�：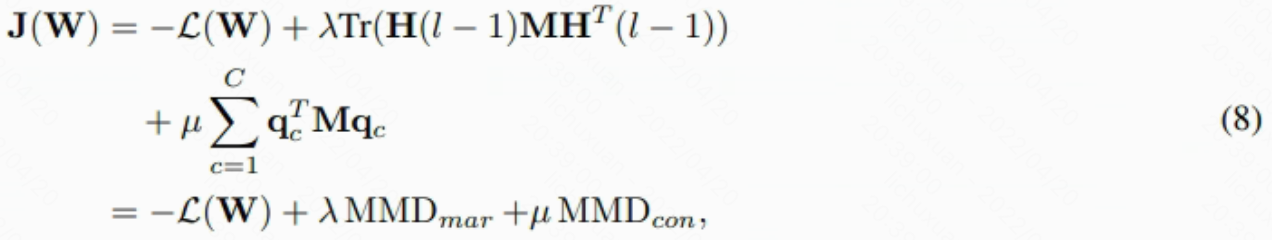

其中和是边缘和条件分布调节参数。通过最小化等式8可以计算W。最终的目标函数不依赖于损失函数的确切形式，并且网络的结构可以轻松地将公式扩展到其他类型的神经网络，例如 CNN 和深度信念网络 (DBN)，以及 MLP。�

Optimization of Deep Transfer Network

The Optimization Procedure

我们首先介绍一些符号。 对于任意训练样本 x，将该样本的最终分类器的后验（条件）概率输出表示为 p�。是C维向量，其中每个维度代表某个类别的后验概率。很容易证明：
=

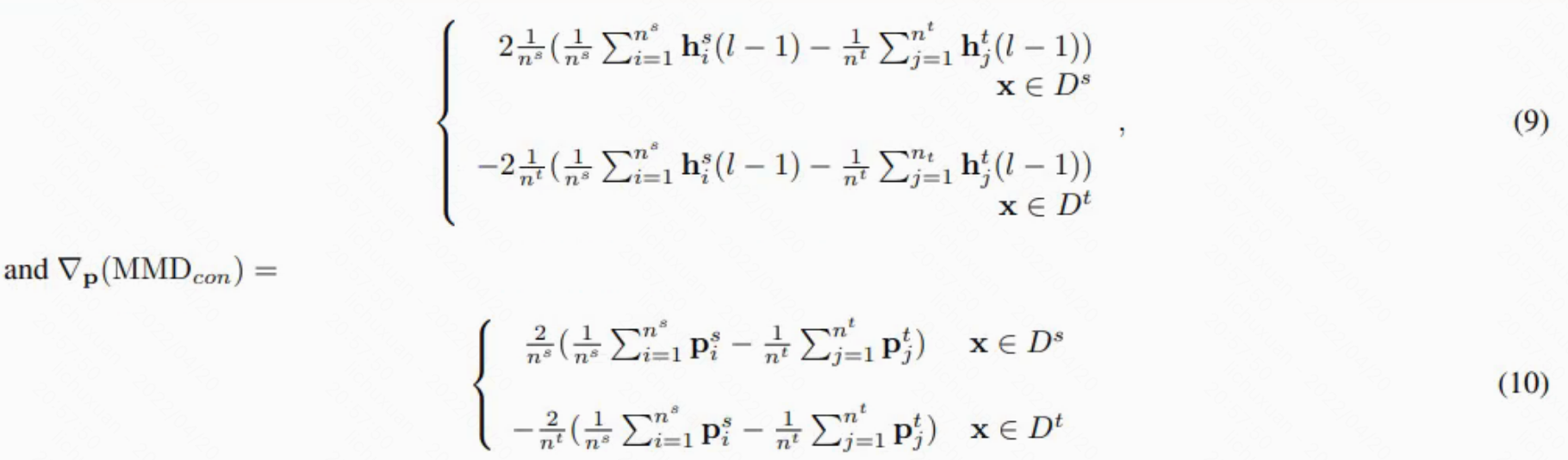
然后我们使用反向传播算法来优化神经网络。 将 W 中的一个元素表示为 Wij 。 Eq.8 的 Wij 的偏导数可以写为�：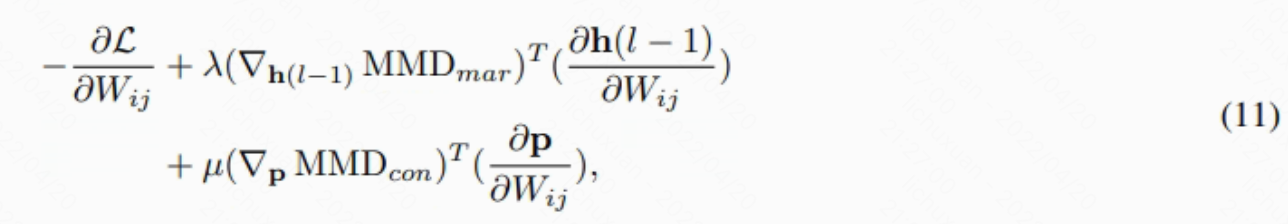

其中和是由h(h-1) 和 p中每个元素对Wij的偏导数组成的向量。如果给定网络的结构，它们可以很容易地计算出来。 我们可以用随机梯度下降优化网络的参数�。

要解决的一个问题是边缘MMD或条件MMD的计算需要考虑所有源和目标样本。这是非常低效的，尤其是当训练数据集很大时。 受小批量随机梯度下降思想的启发，我们将所有样本分成不同的批次。 让 N 是我们想要构建的批次数。 源数据集和目标数据集分为 N 部分。�一个训练批次由源样本和目标样本组成。容易看出：

其中是所有批次的集合，是第k个批次。和是中源数据集和目标数据集的数量。因此，如果所有的mini-batches匹配得非常好，则整个数据集都匹配。我们不再对整个数据集计算MMD，而是对每批数据进行计算。

图2. 构建批次数据的方法。 复制 Dt 中的样本（虚线矩形），以便两个数据集具有相同的大小。 然后通过从两个数据集中随机挑选样本来构建训练批次�

训练批次的构建如下。 首先，较小数据集的样本被随机挑选和复制，使得源数据集和目标数据集具有相同数量的样本。 假设单个批次的大小为 S。然后通过从源数据集中随机选取 S/2 个样本和从目标数据集中随机选取其他 S/2 个样本来填充批次，直到选择所有样本。 批量大小 S 应该足够大，以便每个小批量都可以反映整个数据集的方差。 第 4 节给出了对 S 的实证分析。图 2 说明了构建数据批次的过程。 最后，对小批量应用梯度下降来优化目标函数。�

如第 2 节所述，非迁移神经网络的输出被用作目标样本的伪标签。 毫不奇怪，提供的目标数据的标签越准确，最终分类器的性能就越好。 特别是，DTN 可以将其输出作为输入来改进自身。 我们发现在训练期间迭代更新目标样本的标签可以显着提高 DTN 的性能，尤其是在大规模数据集上。 我们在第 4 节分析 DTN 的收敛性。算法 1 总结了 DTN 的优化。�

Computational Complexity

设为更大数据集的大小，中的批处理数为N。对于每个 mini-batch，计算 Eq.9 和 10 的成本都是 O(S)，其中 S 是一个批次的大小。 在计算批次的梯度时，单个批次中的更多样本总是会导致更高的计算成本。 一批前向传播的计算复杂度也是 O(S)。 由于总共有 N 个批次且 S x N = 2n，因此 DTN 中反向传播在整个数据集上的总计算复杂度为 O(n)�
与其他高阶域自适应算法不同，例如转移联合匹配 (O(n2)) [22] 和基于正则化最小二乘法 (O(n3)) [20] 的自适应正则化，�DTN 的执行时间随着输入样本的数量线性增长。 因此，DTN 适合应用于大规模数据集。�