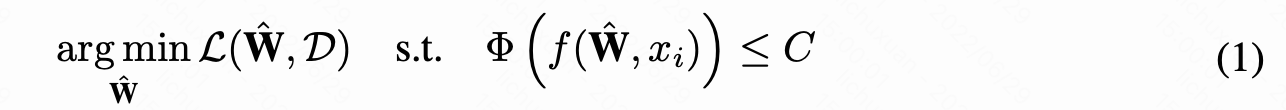一种将延迟作为约束条件的通道裁剪方法。
HALP_paperreading1_yzy.pdf

方法：

对于由对输入进行线性操作、非线性激活和池化组成的L层神经网络。假设在第 l 层有 Nl 个神经元（即输出通道），每个神经元由参数 组成。把整个网络中所有神经元放在一起，得到神经元参数集
。 其中是网络中神经元总数。
给定训练集，C 条件下的网络剪枝问题可转化为 （1） 的优化问题：

其中是裁剪后剩余神经元组成的集合。L是目标损失。f 是表示网络结构的函数。是条件 C（如latency、FLOPs、内存限制） 下的网络映射。
解决上述问题的关键是找到满足条件 C 并使性能下降最小的网络部分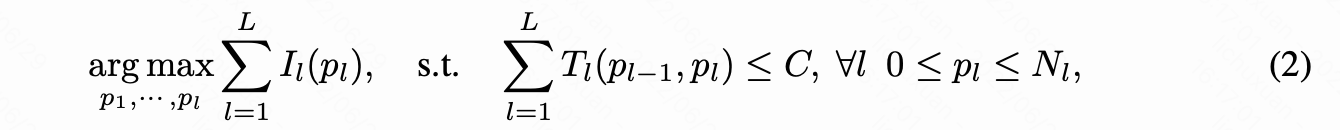

其中 pl 表示第 l 层剩余的神经元数， I**l(pl) 表示 pl** 个神经元对最终精度的最大重要性。
Tl(pl-1, pl) 检查有 pl-1 个输入通道和 pl 个输出通道的层 l 的延迟贡献。
p0 表示第一个卷积块的固定输入通道数

重要性分数

令等式（2）中：。首先用 loss 变化的泰勒展开近似神经元重要性。
Molchanov_Importance_Estimation_for_Neural_Network_Pruning_CVPR_2019_paper.pdf
https://openaccess.thecvf.com/content_CVPR_2019/papers/Molchanov_Importance_Estimation_for_Neural_Network_Pruning_CVPR_2019_paper.pdf

对 BN 层进行修剪，第 l 层的第 n 个神经元的重要性计算公式为：

其中，g 为 weight 的梯度， 和对应 BN 层的 weight 和 bias

为了最大化总重要性，最重要的神经元回保持更高的优先级。
为此，对第 l 层的神经元按照重要性分数从大到小排序，得到：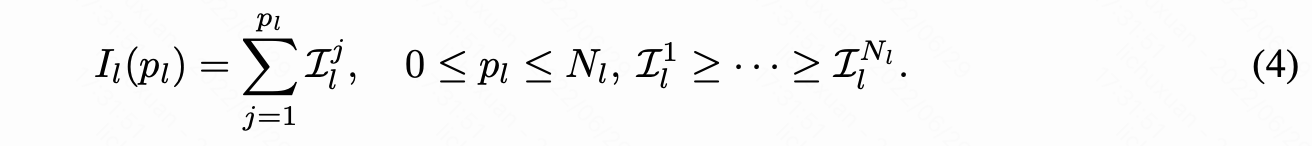

延迟贡献

通过预先测量延迟构建延迟的逐层查找表，从而得到等式（2）中的层延迟。
该层的延迟等于该层中每个神经元的延迟(）之和：

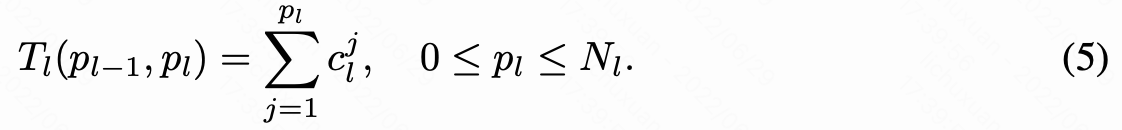
第 l 层中第 j 个神经元的延迟贡献也可以通过延迟查找表计算获得：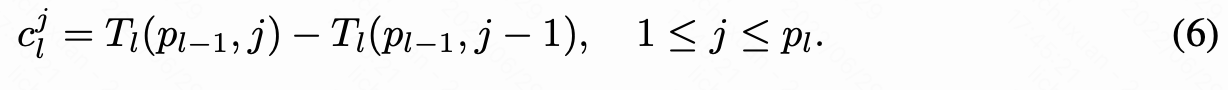

如果裁掉第 l 层中最不重要的神经元，则神经元个数将从 pl 降到 pl-1，那么将减少的延迟作为该神经元的延迟贡献分数。根据重要性顺序将可能减少的延迟分配给层中的神经元。那么该层中最重要的神经元总会有延迟贡献度。于是，找到要保留的神经元是一个组合问题，可以通过考虑延迟和最大化重要性得分来解决。

强背包问题

结合等式 4 的重要性得分和等式 5 的层延迟，等式 2 可以转换为：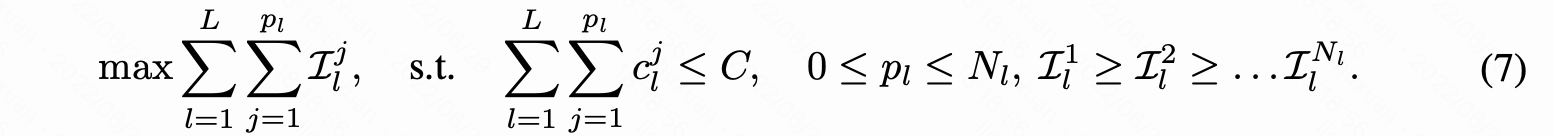

这将整个剪枝过程简化为具有 preceding constraints 的背包问题。该约束来自于这样一个试试：对于第 l 层中排行为 j 的神经元而言， 只有当 排行为 1 至 j-1 的所有神经元都保留在 l 层，剩余的 j+1 至 pl 个神经元都被移除时，排行为 j 的神经元的延迟贡献才成立。这个问题可以通过为每个神经元指定一个在包含之前需要选择的前面的神经元的列表来解决，即选择 j 之前需要先 选择 [1,2,3,…,j-1]

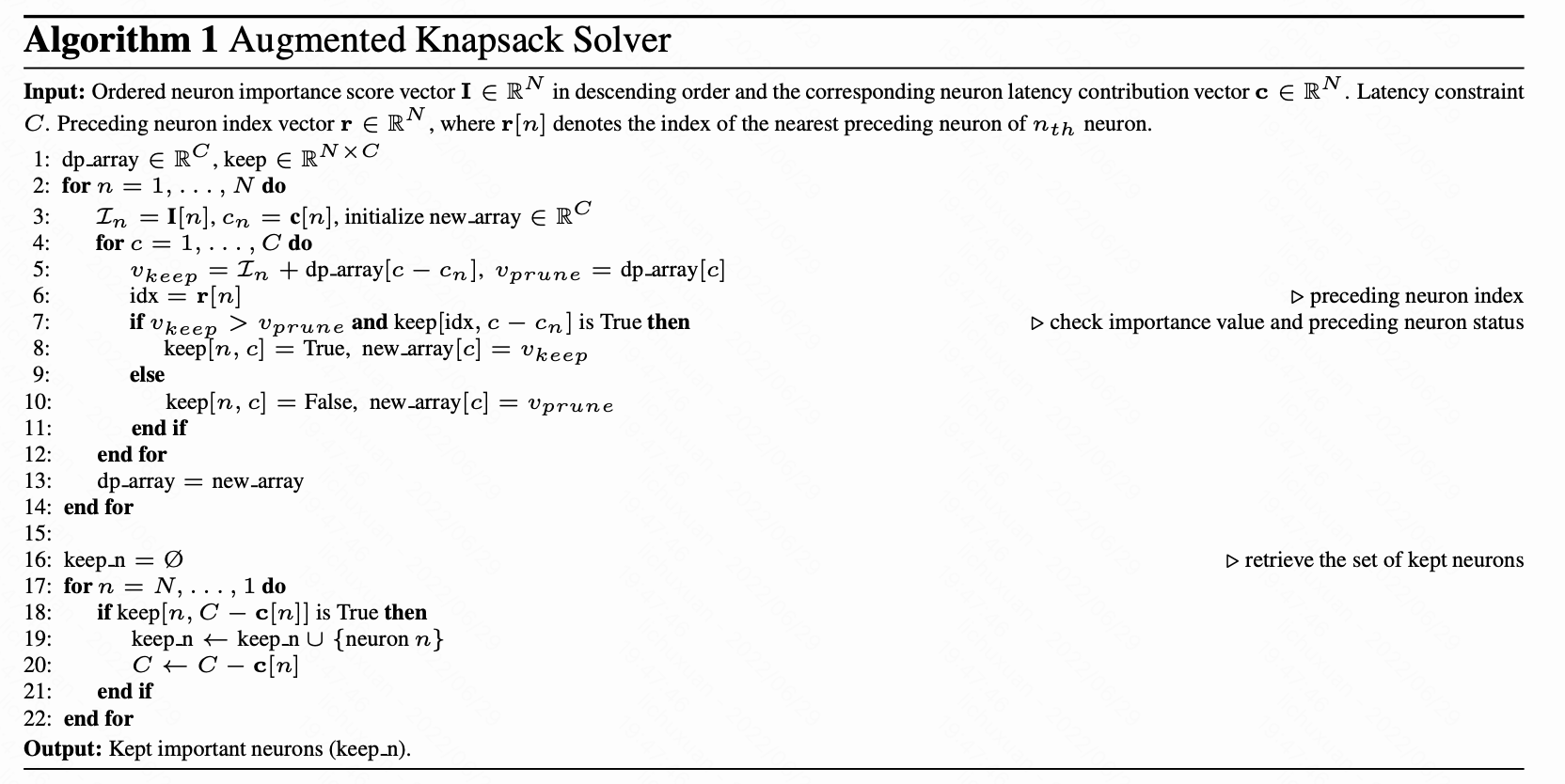
神经元分组

在修剪过程中，单独考虑每个神经元会导致繁重的计算。对神经元进行分组，可以联合考虑和删除其中的一些神经元，从而实现更快的修剪以及等式 7 背包问题求解。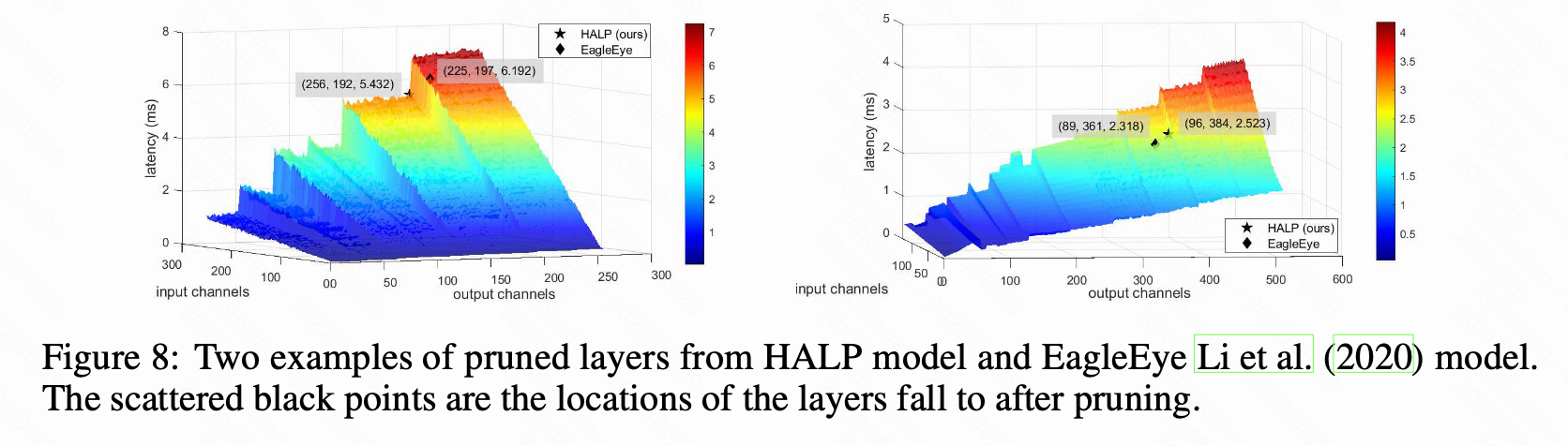

延迟与通道数的增长关系呈阶梯式变化，如图 8。本文将两个延迟 cliffs 之间的神经元数量差异称为延迟步长。 本方法中将层中的 s 个通道作为一个整体进行分组，其中 s 的值等于延迟步长。
神经元按重要性顺序分组。 然后汇总分组的重要性分数和延迟贡献。
在处理 ResNet 中的跳跃连接和 MobielNet 中的分组卷积时，本文不仅将同一层的神经元分在一个组内，还会将连接层中共享相同通道索引的神经元分在同一组。
注意不同层的延迟步长可能不同。
对于跨层分组会使用层中最大的组大小。 与启发式通用分组相比，延迟感知分组可以带来额外的性能优势

神经元分组的一个显着好处是简化了背包问题，该问题与考虑的候选者数量呈线性关系（参见算法 1 的第 2 行）。 例如，通过将ResNet50的神经元分组在一起，（分组）神经元的总数可以从 26,560 个大大减少到只有 215 个，这大大加快了求解器的速度。 随着网络规模的扩大，这种节省可能特别有益

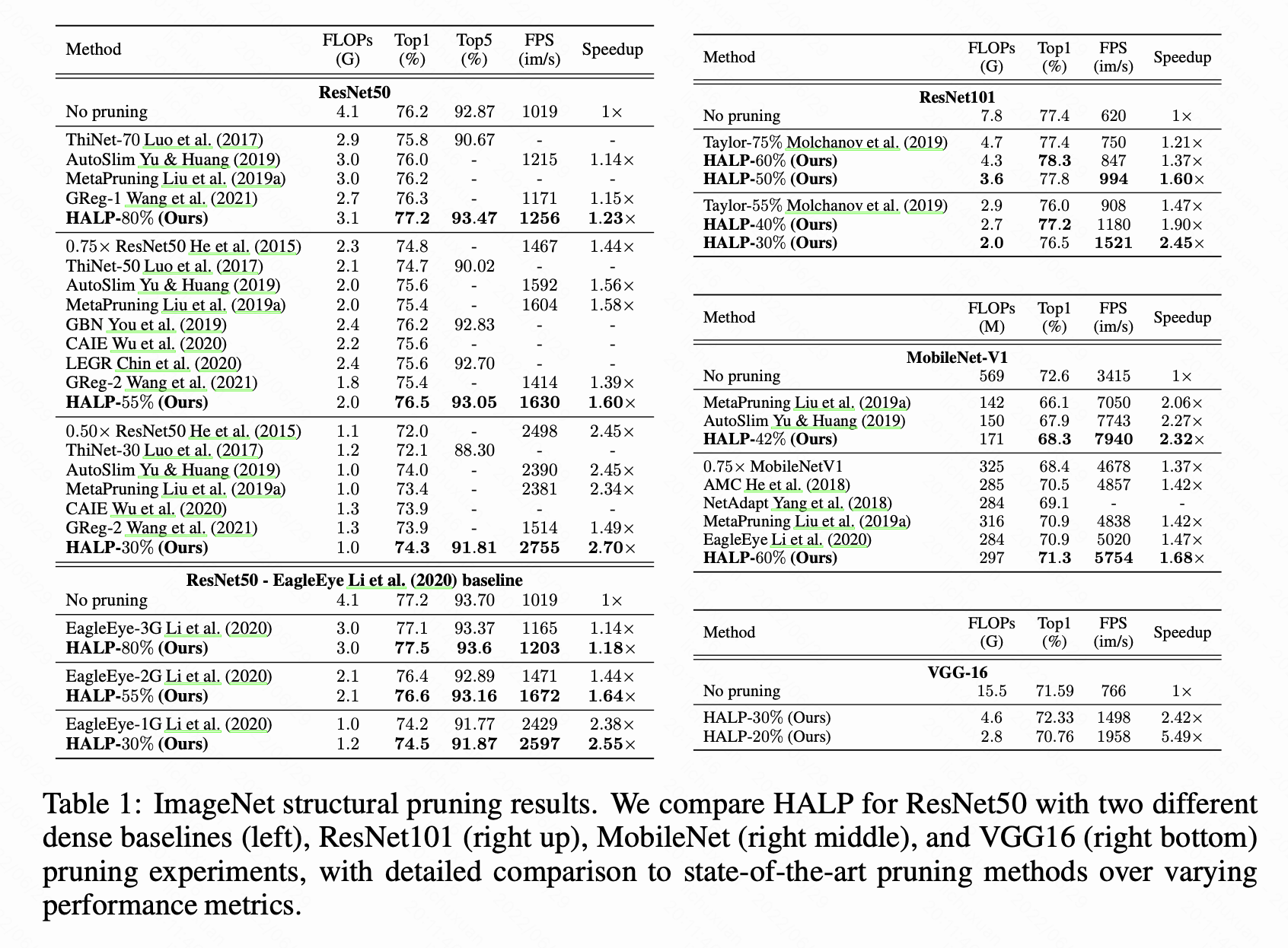
实验结果：

Abstract

HALP：将结构修剪作为全局资源分配优化问题，旨在最大限度降低精度，同时在预先定义的预算下约束延迟。过滤器重要性排序，HALP利用延迟查找表跟踪延迟下降势能和全局显著性得分衡量准确性下降。剪枝过程中，两种方法都能有效评估，从而使我们能够在给定目标约束的报酬最大化问题下对整体结构进行重新规划。这使得问题可以通过增强背包方法解决。

Introduction

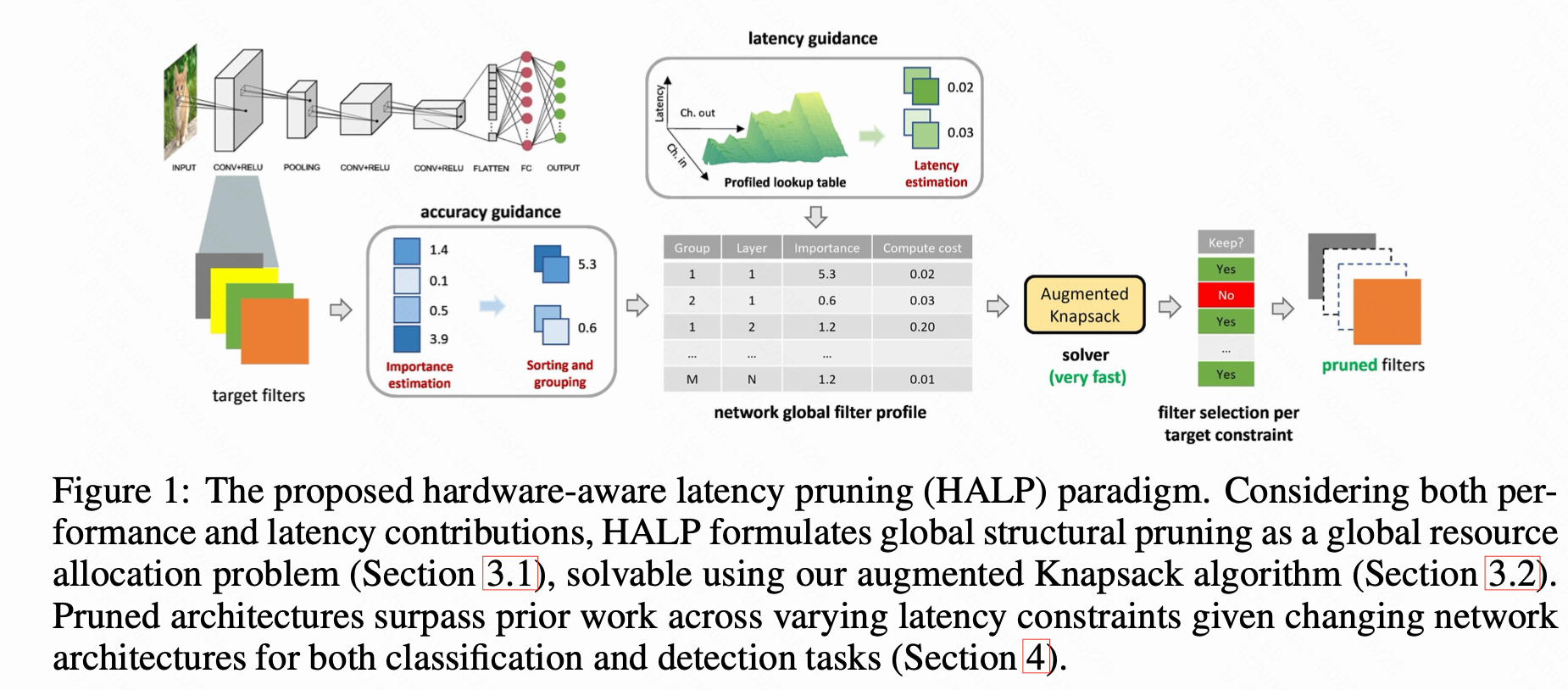
本文研究剪枝，尤其是去除过滤器/神经元的结构化剪枝，可以从off-the-shelf platforms（如GPU）中获益。
剪枝标准：FLOPs
在不同的修剪配置下获得精确的层查找表将有利于最大化性能，同时最小化延迟

修建深层神经网络中的不同层次将导致不同的精度延迟，通常从后一层移除通道对精确度影响较小，对延迟影响较小。

本文提出了硬件感知延迟修剪（HALP），它将修剪作为资源分配优化问题来最大化准确性，同时保持延迟预算。
对于每个修剪后的架构的延迟估计，通过为目标硬件上模型的每一层创建查找表来预先分析操作员级别的延迟值。然后我们为每个神经元组引入一个额外的分数，以反映和鼓励延迟减少。为此，我们首先根据它们的重要性估计对神经元进行排序，然后动态调整它们的延迟贡献。
随着神经元硬件感知延迟曲线的重新校准，在总延迟约束内最大化基于梯度的重要性估计，选择剩余神经元提高准确性。
整个神经元排序在背包范式下可解，为了使层中神经元选择顺序从最重要到最不重要，增强背包求解器，以便剩余神经元到计算延迟保持不变。

Related work

剪枝方法：根据修剪时间不同，目前方法大致可分为三类：1. 剪预训练好的模型， 2. 初始化时剪枝，3. 训练过程中剪枝。 尽管后两个领域取得了显著性进展，但修剪预训练模型仍然是最流行的范例，其结构稀疏性收到了GPU等现成推理平台的青睐
为了提高推理效率，以前的许多剪枝方法都对神经网络进行了修剪，目的是在保持可接受精度的同时，获得较高压缩率。有文章建议使用泰勒展开式测量神经元的重要性，并修剪排名最低的神经元，直至修剪出所需数量的神经元，然而，由于每个神经元/滤波器具有不同的计算能力，压缩比并不能直接转化为计算简化比。
最近有些方法主要关注FLOPs，在计算神经元重要性时考虑FLOPs，惩罚导致高计算的神经元
另一种方法是从一组候选网络中选择最佳修剪网络，然而由于候选网络数量巨大，选择会花费很多时间
此外，这些方法使用FLOPs作为延迟的代理，这通常不准确，因为具有相似FLOPs的网络可能有显著不同的延迟

延迟感知压缩：新兴今天压缩技术将注意力转移到直接删减延迟上，一种流行方法是神经结构搜索（NAS）：根据给定的延迟要求自适应调整网络架构。他们将平台约束纳入架构和参数空间的优化过程，共同优化模型尺寸和精度。尽管有着独特的见解，但与修剪方法相比，NAS方法总体上计算成本高。
面向延迟的修剪也得到越来越多关注。有方法提出一个操作约束下的网络压缩框架，利用贝叶斯优化迭代获得满足约束的压缩超参数。虽然这些方法推动了受延迟约束的剪枝方法的前沿，但在我们剪枝策略的增强下，硬件导致的延迟表面实际上提供了更大的潜力。