算法复杂度

时间复杂度

• O(1) 哈希桶/数组随机寻址（常数）
• O(n) 遍历 （线性）
• O(log(n)) 二分查找， 二叉树（对数）
• O(n*log(n)) 基于比较的排序算法的下界

• O(n^2) 冒泡排序 平方

  时间复杂度的计算是忽略常熟的

• 即 O(n) = O(2n)

  时间复杂度的计算中，高阶复杂度会吞并低阶

• O(n^2) + O(n) = O(n^2)

哈希表

为什么需要hash表

假如有一个学校的系统，有10万个同学，我想要找到其中一个同学，那么就需要遍历中10万个同学，一个个的找，非常花时间。
假如我们根据学生的学号，进行一定的计算，得出一个数组的下标，那么就可以瞬间定位这个元素在数组中的位置。

实现原理

哈希表的底层，就是数组。只不过存储数据的时候，下标是通过hash函数来计算出来的。

哈希函数

hash值产生原理

是根据关键字设计的，有很多种函数，主要的原理就是根据数组的大小求模（就是求余数）运算
(关键字) / (数组大小)
eg： 20048157 / 17 （结果在0-16之间）
数组的大小一般设计为质数，因为需要均匀的散步

hash冲突

算出来的下表，有重复的可能性，这叫做hash 冲突或者hash碰撞，解决办法如下

链表式解决(Separate Chaining)

在数据里面添加一个下一个数据的指针，记录着hash值相同的数据的内存地址
例子：
数据关键字：15 16 22 24
数组大小：7
哈希函数：下标=关键字 mod 数组大小
根据哈希函数计算出的下标：15 -> 1; 16 -> 2；22 -> 1; 24-> 3

那么 15 应该放到数组的索引1的位置，
16 放到索引2的位置
22 放到索引1的位置，但是因为已经放着15，所以在15里面加一个指针，指向22，形成一个链表
24 放到索引3的位置

开放地址法(Open Addressing)

不用next指针，把其他下标的位置都对外开放

• 线程探测法

如果遇到冲突，就往下一个地址寻找空位，新位置=原始位置+i（冲突的次数）

• 平方探测（二次方探测）

如果遇到冲突，就往下一个地址寻找空位，新位置=原始位置+i^2（冲突的次数的平方）

• 双哈希

要设置第二个hash的函数，例如： hash2(key) = R - (key mod R)
R要去比数组尺寸小的质数
比如：R=7: hash2(关键字) = 7 - （关键字 mod 7）
也就是说，二次hash的结果在1-7之前，不会等于0
如果遇到冲突 新位置 = 原始位置 + i.hash2(关键字)

例子：

数据关键字： 15 2 18 28
数组大小： 13
哈希函数：下标 = 关键字 mod 13
哈希函数2: 7 - (关键字 mod 7)
如果遇到冲突， 新位置 = 原始位置 + i.hash2(关键字)

栈（stack）

图文说明

栈是一种只能在一端进行插入和删除操作的特殊的数据结构，按照先进后出的原则，先进入的数据会被压入栈底，最后进入的数据会被放入栈顶。
入栈的时候数据0先进入，出栈的时候反而是数据3先出栈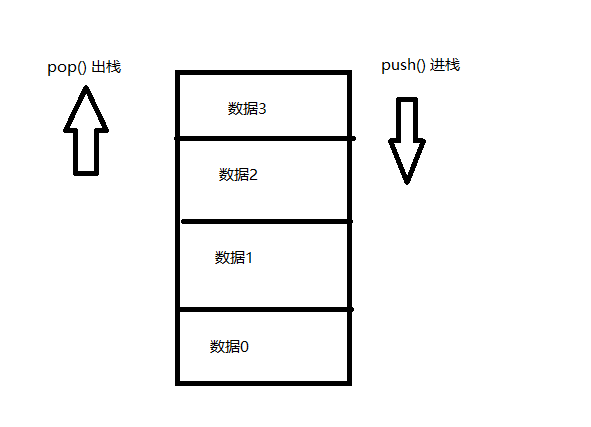

最简单普通的栈

实现代码

package com.data.structure.stackDemo;

public class MyStack {
    private int[] array;
    private int maxSize;
    private int top;

    public MyStack(int maxSize) {
        this.maxSize = maxSize;
        array = new int[maxSize];
        top = -1;
    }

    // push data
    public void push(int value) {
        if (top < maxSize - 1) {
            top += 1;
            array[top] = value;
        }
    }

    // pop data
    public int pop() {
        int result = array[top];
        top -= 1;
        return result;
    }

    // access peek data
    public int peek() {
        return array[top];
    }

    public boolean isEmpty() {
        return top == -1;
    }

    public boolean isFull() {
        return top < maxSize - 1;
    }
}

测试代码

package com.data.structure.stackDemo;

public class MyStackTest {

    public static void main(String[] args) {
        MyStack myStack = new MyStack(3);
        myStack.push(1);
        myStack.push(2);
        myStack.push(3);
        System.out.println(myStack.peek());
        while (!myStack.isEmpty()) {
            System.out.println(myStack.pop());
        }
    }
}

增强栈—追加自动扩容，数据类型

代码实现

package com.data.structure.enhanceStackDemo;

import java.util.Arrays;
import java.util.EmptyStackException;

public class EnhanceStack {

    // define object array for all types data
    private Object[] elementData;
    // stack top pointer
    private int top;
    // stack size
    private int size;

    public EnhanceStack() {
        this.elementData = new Object[10];
        this.top = -1;
        this.size = 10;
    }

    public EnhanceStack(int initialCapacity) {
        if (initialCapacity < 0) {
            throw new IllegalArgumentException("initial capacity can not be zero");
        }

        this.elementData = new Object[initialCapacity];
        this.top = -1;
        this.size = initialCapacity;
    }

    // push data
    public Object push(Object item) {
        // resize current stack
        resize(top + 1);
        elementData[++top] = item;
        return item;
    }

    // pop top element
    public Object pop() {
        Object obj = peek();
        remove(top);
        return obj;
    }

    // delete stack top element
    private void remove(int top) {
        elementData[top] = null;
        this.top--;
    }

    // isEmpty
    public boolean isEmpty() {
        return top == -1;
    }

    // get stack top element
    public Object peek() {
        if (top == -1) {
            throw new EmptyStackException();
        }
        return elementData[top];
    }


    // resize this stack if necessary
    private void resize(int minCapacity) {
        int oldCapacity = size;
        // resize stack if minCapacity is greater than oldCapacity
        if (minCapacity > oldCapacity) {
            // define newCapacity
            int newCapacity = 0;
            // resize capacity two times and check if surpass Integer Max value
            if ((oldCapacity << 1) - Integer.MAX_VALUE > 0) {
                newCapacity = Integer.MAX_VALUE;
            } else {
                newCapacity = (oldCapacity << 1);
            }

            this.size = newCapacity;
            Object[] newArray = new Object[size];
            elementData = Arrays.copyOf(elementData, size);
        }
    }


}

测试代码

package com.data.structure.enhanceStackDemo;

public class EnhanceStackTest {
    public static void main(String[] args) {
        EnhanceStack stack = new EnhanceStack(4);
        stack.push(1);
        //System.out.println(stack.peek());
        stack.push(2);
        stack.push(3);
        stack.push("abc");
        System.out.println(stack.peek());
        stack.pop();
        stack.pop();
        stack.pop();
        System.out.println(stack.peek());
    }
}

队列

图文说明

队列的特征是先进先出（First in First out）,只能在队列的头部进行删除操作，在尾部进行插入操作，以满足先进先出的特征。
需要注意的是，在一个队列中，队头和队尾的位置不一定总是对头在下，队尾在上。
追加万一些数据后，状态如下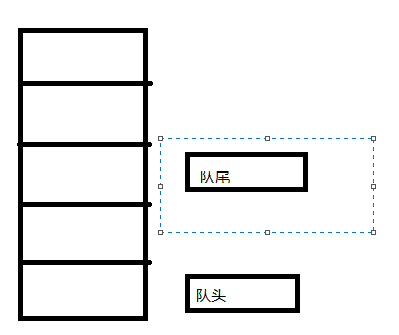

此时如果删除一个元素在追加三个元素，因为队列已满的原因，队尾的指针会指向队头的位置，而队头的指针，因为删除过一个元素的原因，会指向队列的倒数第二个位置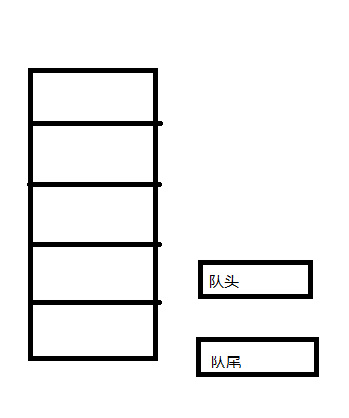

一个简单的队列

代码实现

package com.data.structure.queueDemo;

public class MyQueue {
    private Object[] queArray;
    // queue size
    private int maxSize;
    // front pointer
    private int front;
    // end pointer
    private int rear;
    // exist element in queue
    private int nItems;

    public MyQueue(int size) {
        maxSize = size;
        queArray = new Object[maxSize];
        front = 0;
        rear = -1;
        nItems = 0;
    }

    // insert new element
    public void insert(Object value) throws Exception {
        if (isFull()) {
            throw new Exception("queue is full");
        } else {
            // rear pointer aims to first one index if rear pointer reach queue's margin
            if (rear == maxSize - 1) {
                rear = 1;
            }
            queArray[++rear] = value;
            nItems++;
        }
    }

    public Object remove() {
        Object removeValue = null;
        if (!isEmpty()) {
            removeValue = queArray[front];
            queArray[front] = null;
            front++;

            // reset front pointer into first index if the last one element is removed in queue
            if (front == maxSize) {
                front = 0;
            }
            nItems--;
            return removeValue;
        }
        return removeValue;
    }

    // check front data
    public Object peekFront() {
        return queArray[front];
    }

    public boolean isEmpty() {
        return nItems == 0;
    }


    public boolean isFull() {
        return nItems == maxSize;
    }

    public int getSize() {
        return nItems;
    }
}

测试代码

package com.data.structure.queueDemo;

public class MyQueueTest {
    public static void main(String[] args) throws Exception {
        MyQueue queue = new MyQueue(3);
        queue.insert(1);
        queue.insert(2);
        queue.insert(3);

        System.out.println(queue.peekFront());
        queue.remove();
        System.out.println(queue.peekFront());

        queue.insert(4);
//        queue.insert(5);
    }
}

链表

链表（linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按照现行的顺序存储数据，而是再每一个节点里存储下一个节点的指针。
优点：可以充分利用计算机内存空间，实现灵活的内存动态管理
缺点：失去了随机读取的有限，同时由于链表增加了节点的指针域，空间的开销也会比数组大

单向链表

一个单链表的节点(Node)分为两个部分，第一个部分(data)保存或者显示关于节点的信息，另一个部分存储下一个节点的地址。最后一个节点存储地址的部分指向空值。
单向链表只可向一个方向遍历，一般查找一个节点的时候需要从第一个节点开始每次访问下一个节点，一直访问到需要的位置。而插入一个节点，对于单向链表，我们只提供在链表头插入，只需要将当前插入的节点设置为头节点，next指向原头节点即可。删除一个节点，我们将该节点的上一个节点的next指向该节点的下一个节点。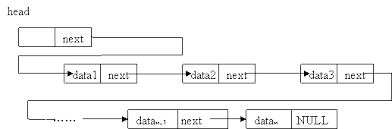

代码演示

// 单链表代码

package com.data.structure.linkedListDemo.singleLinkedList;

public class SingleLinkedList {
    private int size; // LinkedList size
    private Node head; // head node

    public SingleLinkedList() {
        this.size = 0;
        this.head = null;
    }

    // add node in list head
    public Object addHead(Object obj) {
        Node newHead = new Node(obj);
        if (size != 0) {
            newHead.setNext(head);
        }
        this.head = newHead;
        size++;
        return newHead;
    }

    // delete node in list head
    public Object deleteHead() {
        if (size != 0) {
            Node newHead = this.head.getNext(); // this newHead is actually the second one node in LinkedList, and it will be the first one after delete operation
            Object oldHeadData = this.head.getData(); // the old head data
            this.head.setNext(null);
            this.head = newHead;
            size--;
            return oldHeadData;
        } else {
            return null;
        }
    }

    // find specified node and return if exists, otherwise return null
    public Node find(Node node) {
        Node currentNode = this.head;
        int tempSize = this.size;

        while (tempSize > 0) {
            if (node == currentNode) {
                return currentNode;
            } else {
                currentNode = currentNode.getNext();
            }
            tempSize--;
        }
        return null;
    }

    // delete specified node
    public boolean delete(Node node) {
        if (size == 0) {
            return false;
        }

        // find parameter node's previous node
        Node current = head;
        Node previous = head;
        while (current.getData() != node.getData()) {
            if (current.getNext() == null) {
                return false;
            } else {
                previous = current;
                current = current.getNext();
            }

            if (current == head) {
                head = current.getNext();
            } else {
                previous.setNext(current.getNext());
                size--;
            }
        }
        return true;
    }
}

节点代码

package com.data.structure.linkedListDemo.singleLinkedList;

import java.util.Objects;

public class Node {
    private Object data;
    private Node next; // next node pointer

    public Node(Object data) {
        this.data = data;
    }

    public Object getData() {
        return data;
    }

    public void setData(Object data) {
        this.data = data;
    }

    public Node getNext() {
        return next;
    }

    public void setNext(Node next) {
        this.next = next;
    }

}

树

书的定义以及相关概念

为什么需要树

前面我们介绍数组的数据结构，我们知道对于有序数组，查找很快，并介绍可以通过二分法查找，但是想要在有序数组中插入一个数据项，就必须先找到插入数据项的位置，然后将所有插入位置后面的数据项全部向后移动一位，来给新数据腾出空间，平均来讲要移动N/2次，这是很费时的。同理，删除数据也是。

然后我们介绍了另外一种数据结构——链表，链表的插入和删除很快，我们只需要改变一些引用值就行了，但是查找数据却很慢了，因为不管我们查找什么数据，都需要从链表的第一个数据项开始，遍历到找到所需数据项为止，这个查找也是平均需要比较N/2次。

那么我们就希望一种数据结构能同时具备数组查找快的优点以及链表插入和删除快的优点，于是 树 诞生了。

图解术语

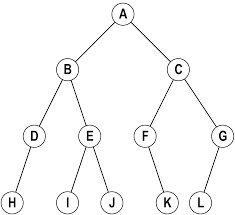
1. 路径：顺着节点的边从一个节点走到另一个节点，所经过的节点的顺序排列就称为“路径”。比如A到B之间的线段
2. 根：树顶端的节点称为根。一棵树只有一个根，如果要把一个节点和边的集合称为树，那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
3. 父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；B是D的父节点。
4. 子节点：与上面定义翻一下，D是B的子节点
5. 兄弟节点：具有相同父节点的节点互称为兄弟节点；比如上图的D和E就互称为兄弟节点。
6. 叶节点/叶子节点：没有子节点的节点称为叶节点，也叫叶子节点，比如上图的H、I，J，K，L都是叶子节点。
7. 子树：每个节点都可以作为子树的根，它和它所有的子节点、子节点的子节点等都包含在子树中。
8. 层次：从根开始定义，根为第一层，根的子节点为第二层，以此类推。
9. 深度：对于任意节点n,n的深度为从根到n的唯一路径长，根的深度为0； 比如B的深度就是1，H的深度就是3
10. 高度：对于任意节点n,n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；比如D的深度就是1，A的深度就是3

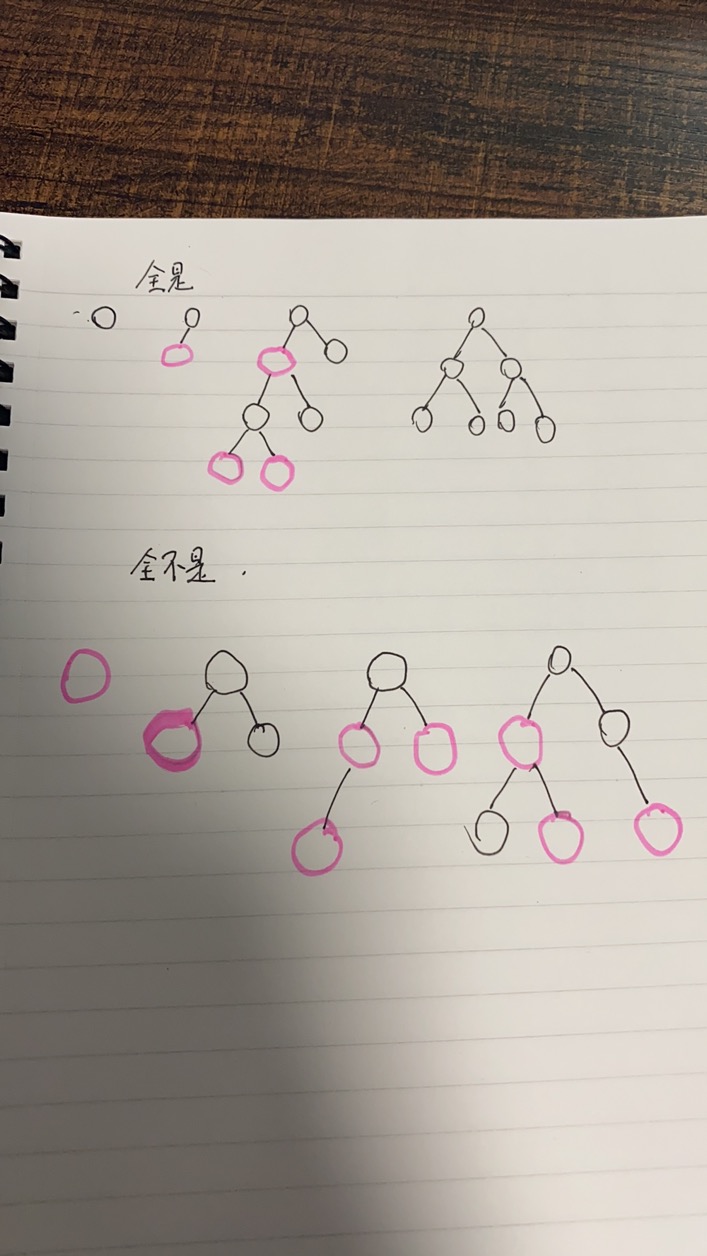
二叉树

定义

二叉树：树的每个节点最多只能有两个子节点，
如果我们给二叉树加一个额外的条件，就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。
二叉搜索树要求：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

遍历方式

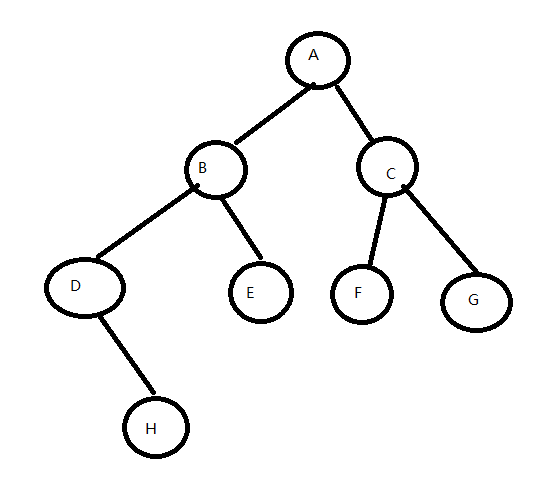
1. 前序遍历：根节点 -> 左子树 -> 右子树 （ABDHECFG）
2. 中序遍历：左子树 -> 根节点 -> 右子树 （DHBEAFCG）
3. 后序遍历：左子树 -> 右子树 -> 根节点 （HDEBFGCA）

   代码实现

   节点代码 ```java package com.data.structure.tree.binaryTree;

public class Node { private int data; private Node leftChild; private Node rightChild; boolean isDeleted;

public Node(int data) {
    this.data = data;
    this.isDeleted = false;
}

public void display() {
    System.out.println(data);
}

public int getData() {
    return data;
}

public void setData(int data) {
    this.data = data;
}

public Node getLeftChild() {
    return leftChild;
}

public void setLeftChild(Node leftChild) {
    this.leftChild = leftChild;
}

public Node getRightChild() {
    return rightChild;
}

public void setRightChild(Node rightChild) {
    this.rightChild = rightChild;
}

public boolean isDeleted() {
    return isDeleted;
}

public void setDeleted(boolean deleted) {
    isDeleted = deleted;
}

}

树的代码
```java
package com.data.structure.tree.binaryTree;

public class BinaryTree implements Tree{

    private Node root;

    @Override
    public Node find(int key) {
        Node current = root;
        while (current != null) {
            if (current.getData() > key) { // search leftChild tree when key is smaller than current node
                current = current.getLeftChild();
            } else if(current.getData() < key) {
                current = current.getRightChild();
            } else {
                if (!current.isDeleted) {
                    return current;
                }
            }
        }
        return null;
    }

    @Override
    public boolean insert(int key) {

        Node newNode = new Node(key);

        if (root == null) { // add newNode to root if this tree has no one node
            root = newNode;
            return true;
        } else {
            Node currentNode = root;
            Node parentNode;

            while (currentNode != null) {
                parentNode = currentNode;

                // search leftChild when key is larger than current
                if (currentNode.getData() > key) {

                    // if leftChild is null then set newNode into it
                    currentNode = currentNode.getLeftChild();   // this operation is for loop search
                    if (currentNode == null) {
                        parentNode.setLeftChild(newNode);
                        return true;
                    }
                } else if(currentNode.getData() < key) {
                    currentNode = currentNode.getRightChild();
                    if (currentNode == null) {
                        parentNode.setRightChild(newNode);
                        return true;
                    }
                }
            }
        }
        return false;
    }

    @Override
    public boolean delete(int key) {
        Node node = find(key);
        if (node != null) {
            node.setDeleted(true);
            return true;
        }
        return false;
    }

    @Override
    public Node findMax() {
        Node current = root;
        Node maxNode = current;
        while (current != null) {
            maxNode = current;
            current = current.getRightChild();
        }
        return maxNode;
    }

    @Override
    public Node findMin() {
        Node current = root;
        Node minNode = current;
        while (current != null) {
            minNode = current;
            current = current.getLeftChild();
        }
        return minNode;
    }

    @Override
    public void showTree(Node node) {
        if (!node.isDeleted) {
            System.out.println(node.getData());
        }
        if (node.getLeftChild() != null) {
            showTree(node.getLeftChild());
        }
        if (node.getRightChild() != null) {
            showTree(node.getRightChild());
        }
    }

    @Override
    public Node getRootNode() {
        return this.root;
    }
}

测试代码

package com.data.structure.tree.binaryTree;

public class BinaryTreeTest {
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.insert(5);
        binaryTree.insert(6);
        binaryTree.insert(3);
        binaryTree.insert(1);

        binaryTree.showTree(binaryTree.getRootNode());

//        int data = binaryTree.find(6).getData();
//        print(data);

        binaryTree.delete(1);
        binaryTree.showTree(binaryTree.getRootNode());
    }

    public static void print(int obj) {
        System.out.println(obj);
    }
}

B树

定义

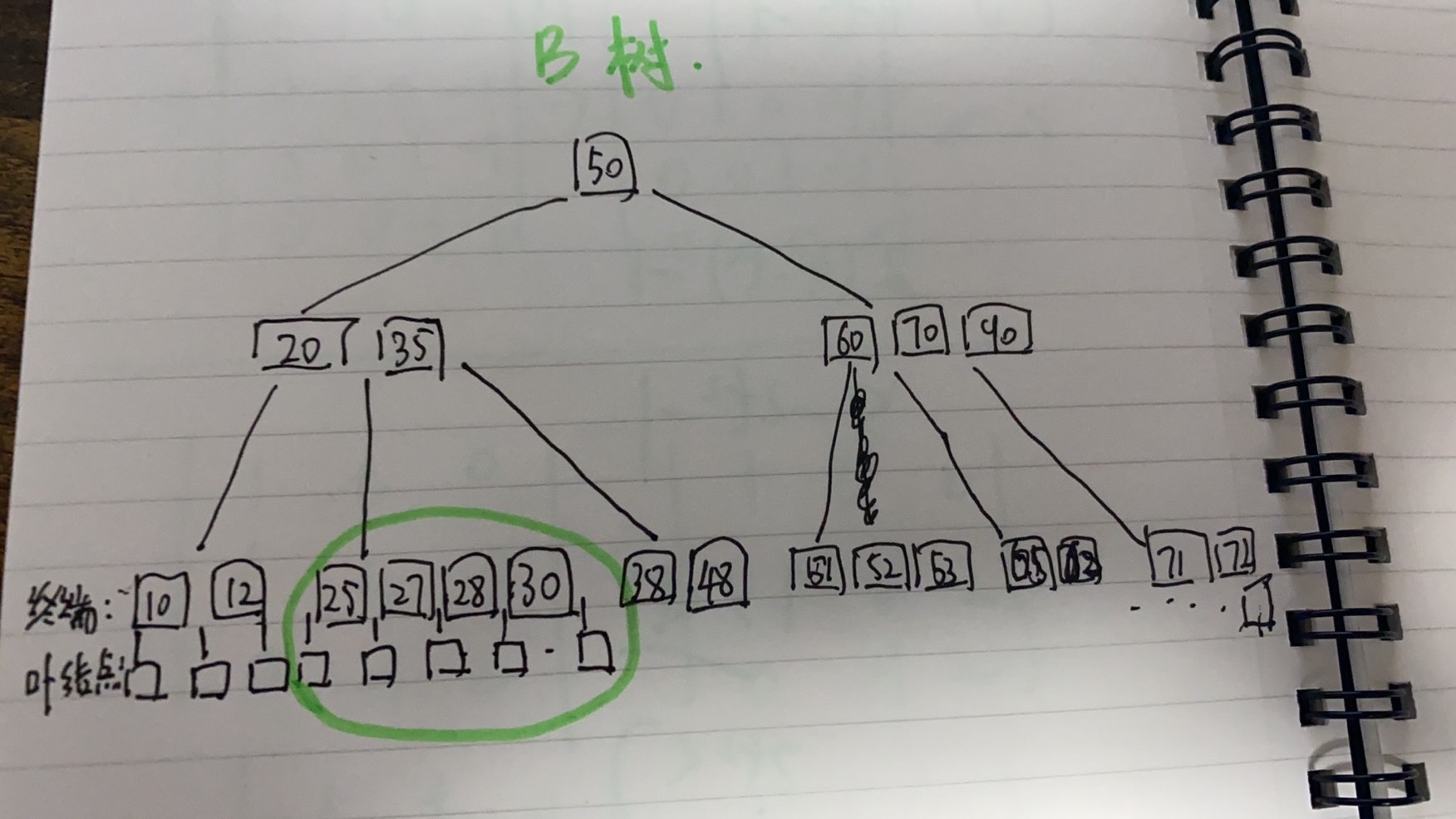
B树（B-树）是一种平衡的多路查找树，B树中的所有节点的子树个数的最大值称为B的阶（此树的节点 最多 有多少个孩子结点（子树））。如图所示，再20 35 这个节点上面，其子树或者说子节点，最多达到了5个，所以是5阶
B树有如下特征

1. 树中每个节点至多有m-1个关键字（就是节点上面的数字），即m棵子树（叶节点也算B树的节点，最然没有存储数据,计算阶的时候需要包含叶节点）
2. 除根节点外，所有非叶节点至少含有m/2 - 1 个关键字，即m/2棵子树（根节点的关键字可以小于m/2 - 1，除不尽的向上取整，可以没有子树，如果有子树，则至少有两棵）
3. 所有叶节点都再同一层上（各子树没有高度差，绝对平衡）。叶节点不带信息，实际上不存在，可以堪称查找失败的节点
4. 所有非叶节点的结构是：

n是该节点关键字的个数
Ki（i=1,2,3,4….）为节点的关键字，且从小打到排列
Pi（i=1,2,3,4….）为指向子树根节点的指针，要比K多一个

B树的插入

例子：B树的节点关键字的个数是m/2 - 1 <= n <= m-1, 5阶B树节点关键字的个数是2-4，根节点的关键字个数是1 - 4，
注意：查找失败的叶节点将被省略。插入的数据会被从小到大排列
分裂方法：从中间位置，讲源节点的关键字分为两个部分，左边的关键字再原节点中，右边的关键字放在新节点中，中间的节点就插入到原节点的父节点。
如果上述的操作导致父节点的关键字个数也超出了上线，则堆父节点进行分裂操作，直到这个过程传递到欧根节点，如果根节点也超过了上线，则创建新的根节点，树的高度将增加一层。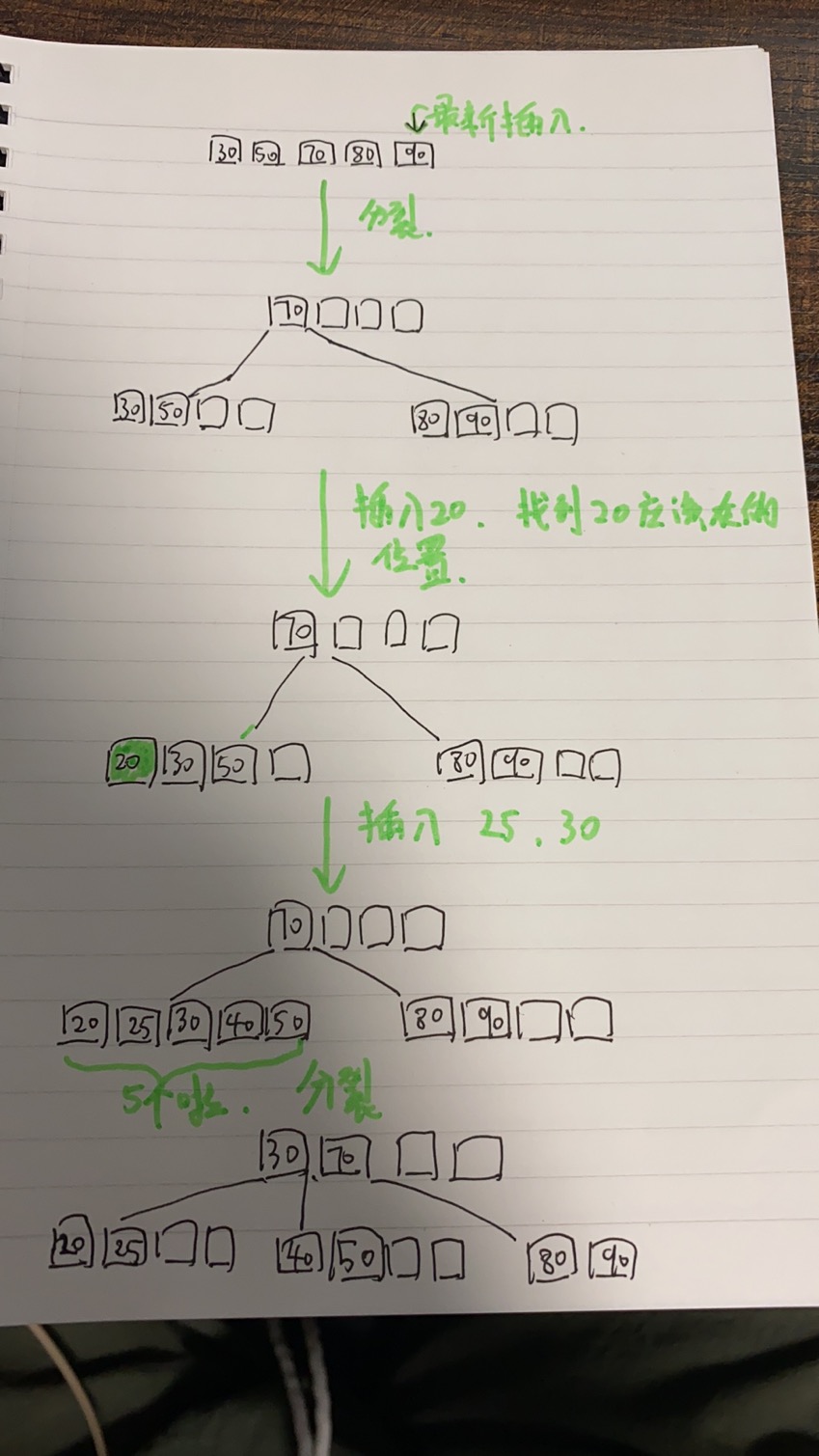

B树的删除

1. 如果待删除的关键字在终端节点中，并且该终端节点的关键字个数大于 m/2 -1 , 直接从该节点中删除该关键字
2. 如果待删除的关键字在终端节点中，并且该终端节点的关键字个数等于 m/2 -1，而与该节点相邻的兄弟（左或者右）节点中关键字的个数大于 m/2 -1 ，则从兄弟节点中借一个关键字

1. 如果待删除的关键字在终端节点中，并且该终端节点的关键字个数等于 m/2 -1，而与该节点相邻的兄弟（左活右）节点的关键字个数也等于 m/2 -1。把当前节点和相邻节点在加上父节点中的关键字合并。如果这次合并导致父节点的关键字个数小于 m/2 -1，则继续合并父节点，知道这个过程传递到根节点

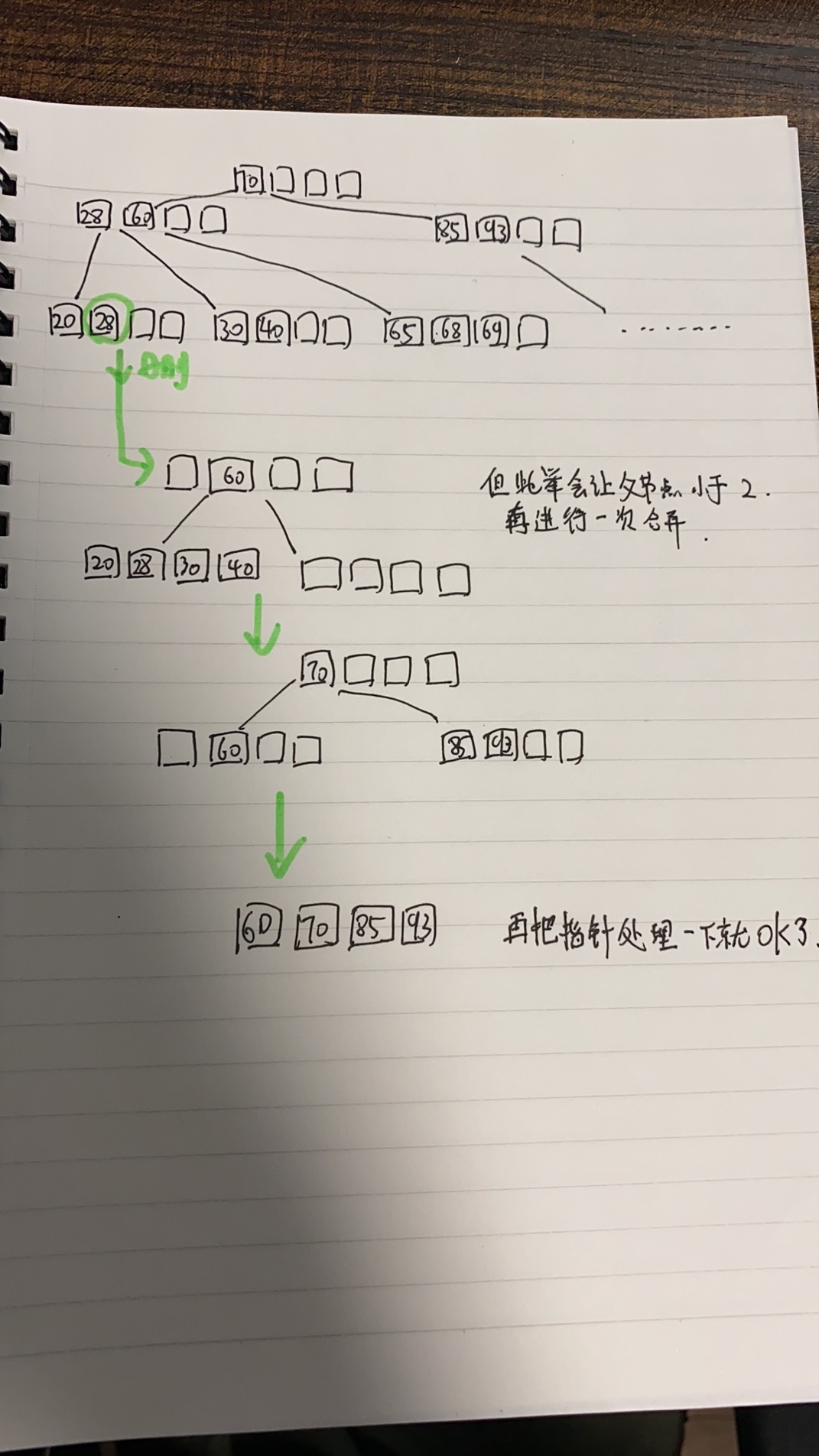
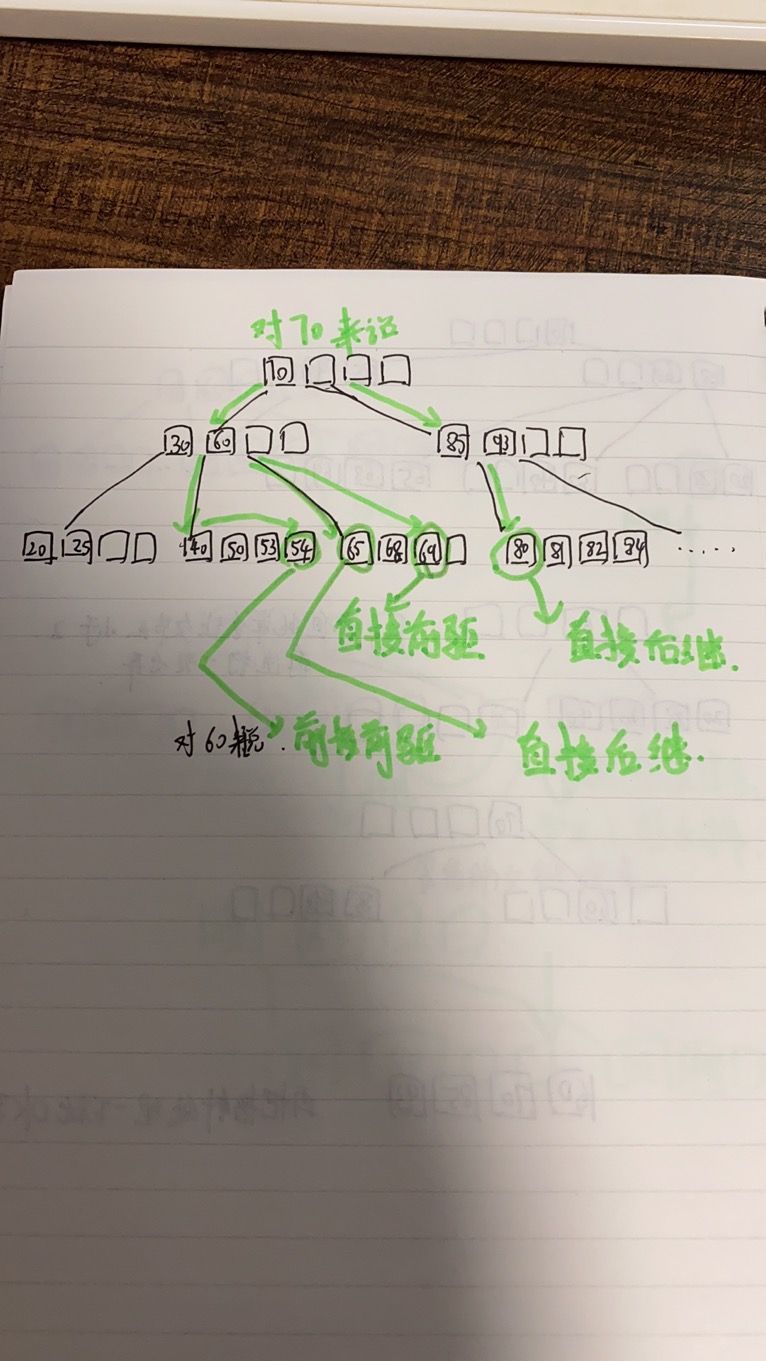
1. 如果待删除的关键字不在终端节点中，则用该关键字的直接前驱或直接后继来代替被删除的关键字

• 直接前驱：当前关键字左侧指针所指向的子树中最右下的关键字
• 直接后继：当前关键字右侧指针所指向的子树中最左下的关键字

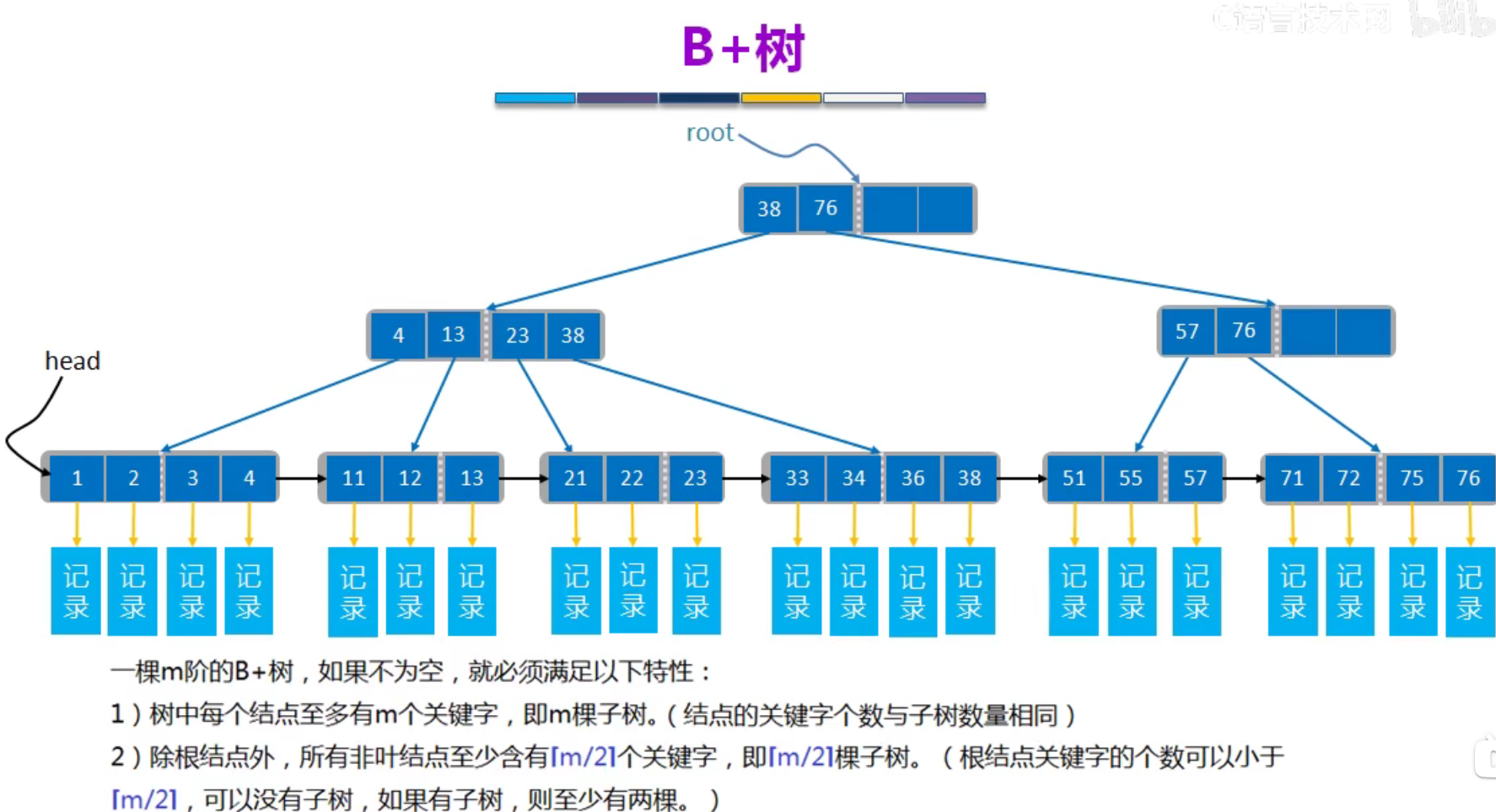
B+树

红黑树

红黑树与二叉搜索树(BST binary search tree)

红黑树首先是一棵BST，其增删查有如下特点
查找方法=BST查找
插入方法=BST查找+红黑树插入fixup
删除方法=BST删除+红黑树删除fixup

红黑树优势

查找，插入，删除的时间复杂度均为O(logn)
插入修正最多旋转两次，插入修正旋转的时间复杂度是O(1)
伤处修正最多旋转三次，删除袖章的旋转的时间复杂度是O(1)

红黑树的性质

1. 节点是红色或者黑色
2. 根节点是黑色的
3. 规定叶子节点NIL是黑色的
4. 每个红色节点的子节点都是黑色
5. 从任一节点到叶子节点的所有路径上都包含相同数目的黑色节点（黑高相同）

总结: 根为黑 红子为黑 黑高相同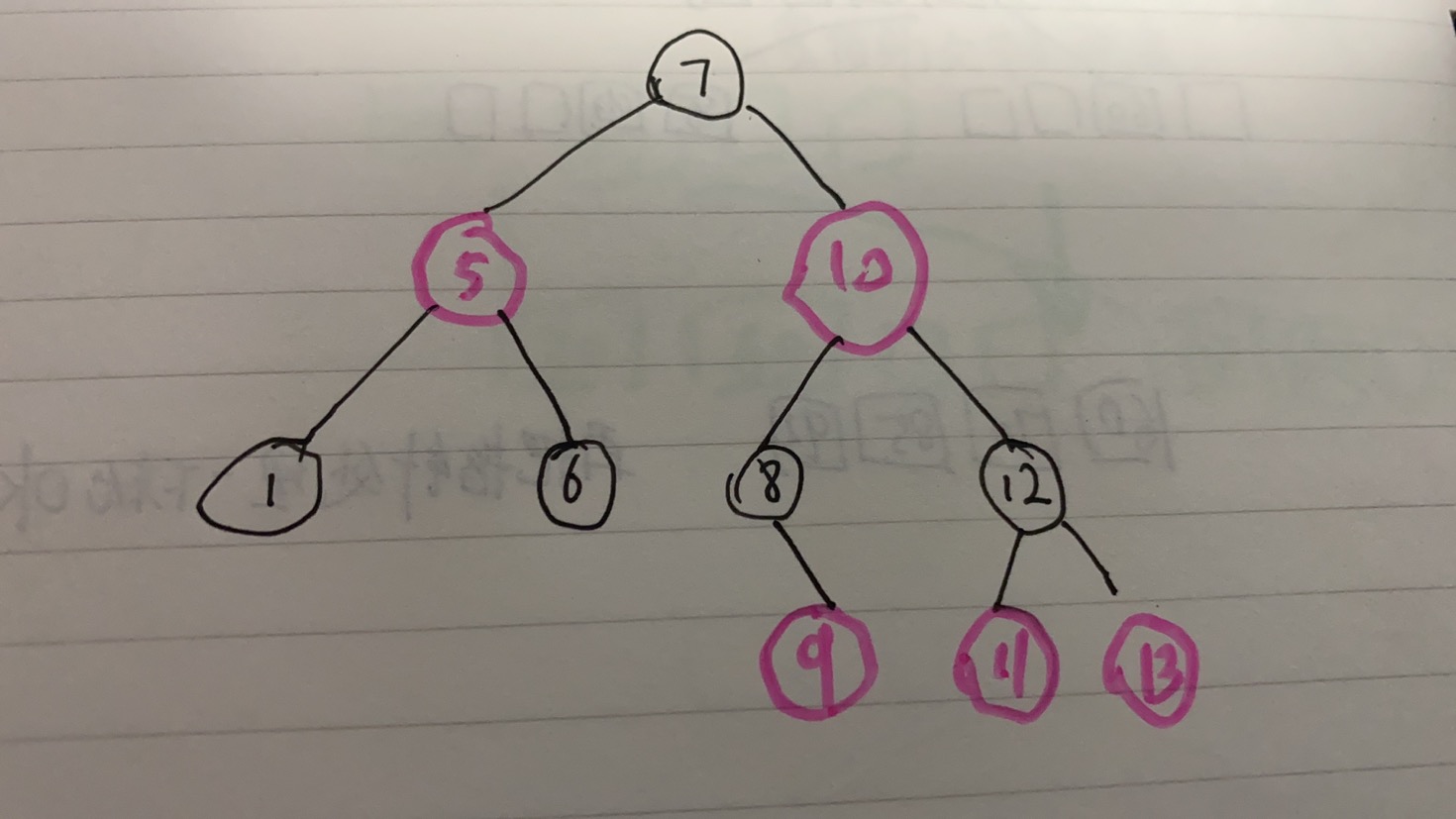

推论

1. 红黑树中可以没有红色节点
2. 节点不存在(Nil) or 存在且为黑 ===> 统一称这个位置为黑色
3. 树中一定有黑色存在，若root==NIL时，root此时也可以看作黑色
4. 红色节点没有红孩子，也没有红父亲
5. 任意一条路径上不可能有两个连续的红节点
6. 红色节点的父节点必然存在且为黑色
7. 黑色节点可以连续存在
8. 最长路径至多是最短路径的两倍

• 证明：
  • 假设红黑树中根节点黑高是h，最短路径是L1，最长路径为L2，若L1尽可能短，那么L1上全是黑色节点，则L1长度为h；L2尽可能厂，则L2上必然是黑红相间交替出现，这是为了保证根节点在任一路径黑高相同。则此时，L2想染正好是L1的两倍，即2h

    案例

    

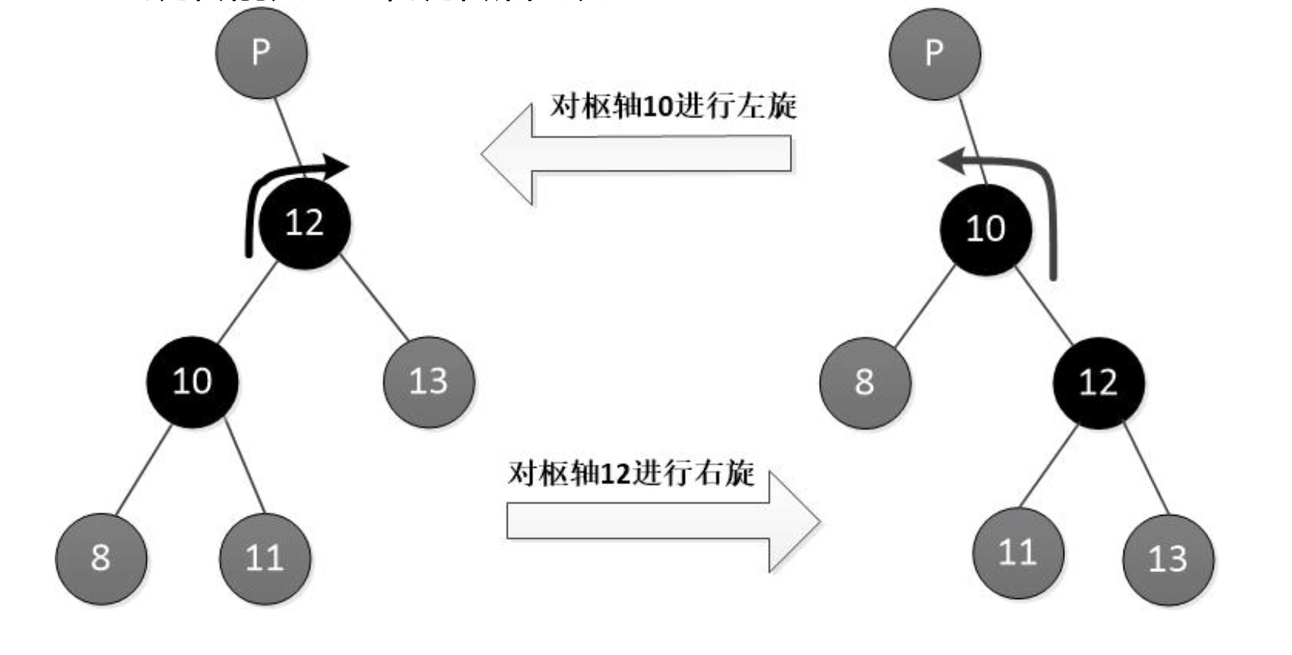
左旋右旋

• 作用

修复红黑树局部不平衡的核心操作

• 旋转性质
  • 从枢轴位置上看：
    • 左旋：左子树高度+1，右子树高度-1
    • 右旋：右子树高度+1，左子树高度-1
  • 旋转前后都是BST

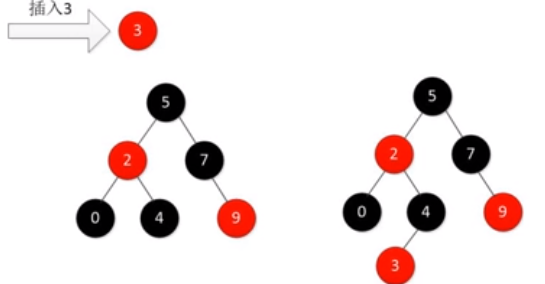
插入

原则：插入删除原则，能直接染色解决则染色解决；若不能直接染色解决，在考虑旋转，尽量把问题控制在局部进行。

1. 步骤1，类比二叉搜索树，插入新节点，且新节点的颜色我们规定为红色

1. 进行插入修正rb_insert_fixup

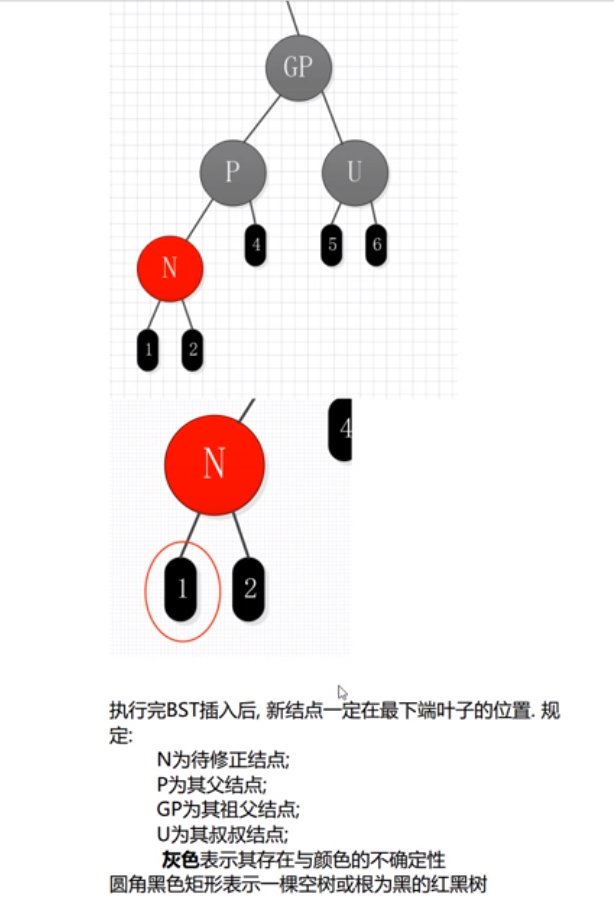
1. 插入分情况讨论

• 情形1：父节点为NULL，即N是根节点

直接将N染成黑色即可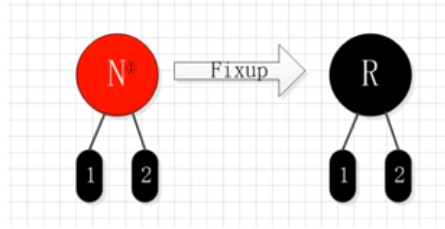

• 情形2：父节点P为黑色，那么说明都不需要做，直接返回

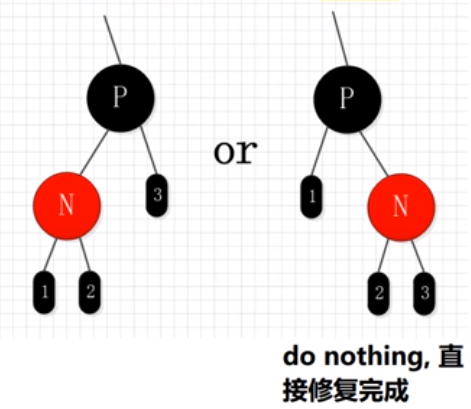
• 情形3：如果父节点P是红色，则祖父节点GP必然存在且为黑
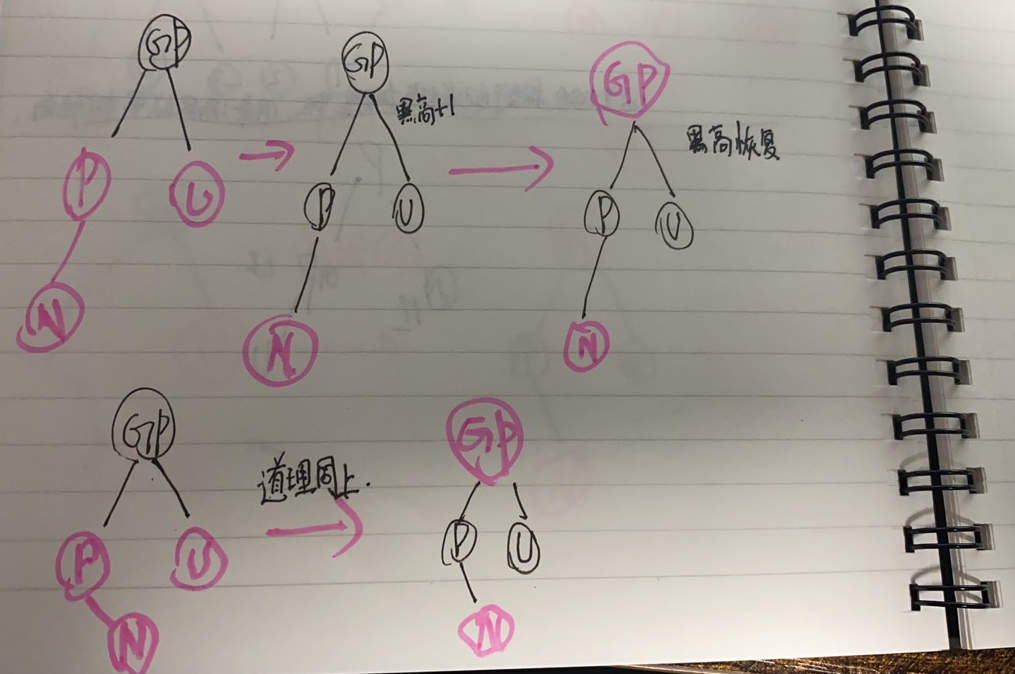
  • a.若父节点P是祖父节点GP的左孩子
    • 【1】. 若叔叔节点U存在且为红色，则将P和U同时染色（此时黑高会变化请注意），然后再将祖父节点染成红色，将黑高变回来

  - 【2】. 若叔叔节点U不存在 or 叔叔节点存在且为黑色；N为父节点P的**右孩子**

此时左旋父节点P，那么会满足【3】的情况，那么交给【3】来处理剩下的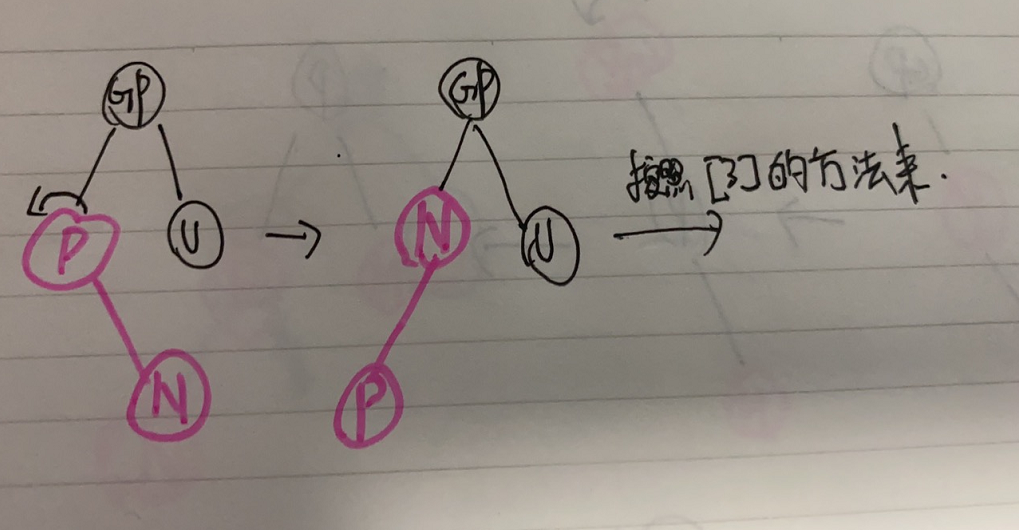

  - 【3】. 若叔叔节点U不存在 or 叔叔节点存在且为黑色；N为父节点P的**左孩子**

左侧多出来一个红色节点，想办法把其中一个挪到右侧，皆大欢喜。方法如下
父节点P变为黑色
祖父节点GP为红色
对祖父节点GP进行右旋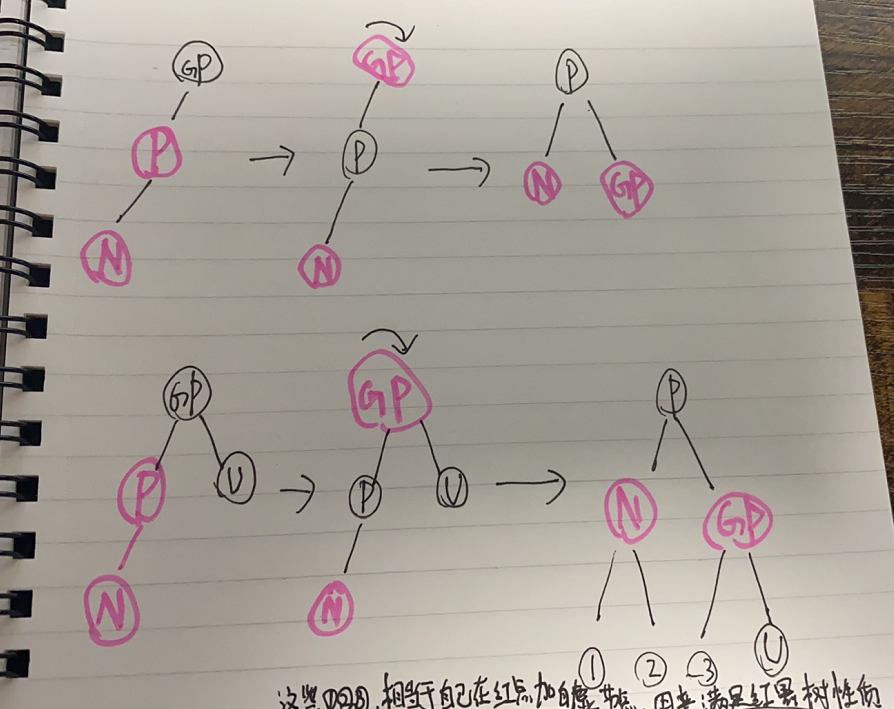

• !a. 和上面的a左右颠倒一下就是剩下的插入情况。

删除

参考文章