1. 简介

表现最稳定的排序算法之一，因为无论什么数据进去都是O(n2)的时间复杂度，所以用到它的时候，数据规模越小越好。
唯一的好处可能就是不占用额外的内存空间。
理论上讲，选择排序可能也是平时排序一般人想到的最多的排序方法。

2. 算法描述

1. 从待排序序列中，找到关键字最小的元素
2. 如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换
3. 从余下的 N - 1 个元素中，找出关键字最小的元素，重复(1)、(2)步，直到排序结束

n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。

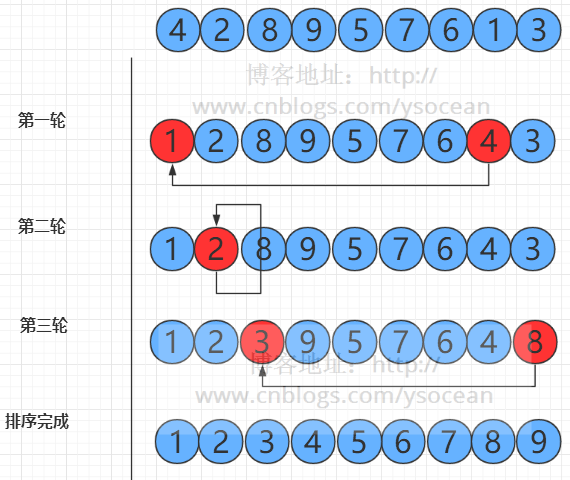
3. 算法描述

1. 初始状态：无序区为R[1..n]，有序区为空；
2. 第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。
3. 该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
4. n-1趟结束，数组有序化了。

package com.ys.sort;
public class ChoiceSort {
    public static int[] sort(int[] array){
        //总共要经过N-1轮比较
        for(int i = 0 ; i < array.length-1 ; i++){
            int min = i;
            //每轮需要比较的次数
            for(int j = i+1 ; j < array.length ; j++){
                if(array[j]<array[min]){
                    min = j;//记录目前能找到的最小值元素的下标
                }
            }
            //将找到的最小值和i位置所在的值进行交换
            if(i != min){
                int temp = array[i];
                array[i] = array[min];
                array[min] = temp;
            }
            //第 i轮排序的结果为
            System.out.print("第"+(i+1)+"轮排序后的结果为:");
            display(array);
        }
        return array;
    }
    //遍历显示数组
    public static void display(int[] array){
        for(int i = 0 ; i < array.length ; i++){
            System.out.print(array[i]+" ");
        }
        System.out.println();
    }
    public static void main(String[] args){
        int[] array = {4,2,8,9,5,7,6,1,3};
        //未排序数组顺序为
        System.out.println("未排序数组顺序为：");
        display(array);
        System.out.println("-----------------------");
        array = sort(array);
        System.out.println("-----------------------");
        System.out.println("经过选择排序后的数组顺序为：");
        display(array);
    }
}

4. 性能分析

选择排序和冒泡排序执行了相同次数的比较：N*（N-1）/2，但是至多只进行了N次交换。

当 N 值很大时，比较次数是主要的，所以和冒泡排序一样，用大O表示是O(N2) 时间级别。但是由于选择排序交换的次数少，所以选择排序无疑是比冒泡排序快的。当 N 值较小时，如果交换时间比选择时间大的多，那么选择排序是相当快的。

1. 最佳情况：T(n) = O(n2)
2. 最差情况：T(n) = O(n2)
3. 平均情况：T(n) = O(n2)