• 性质：

    1. 左子树<根节点
    2. 右子树>根节点

  • 用途：解决与排名有关的检索需求

结构操作

  • 插入
    • 例 ： 插入10

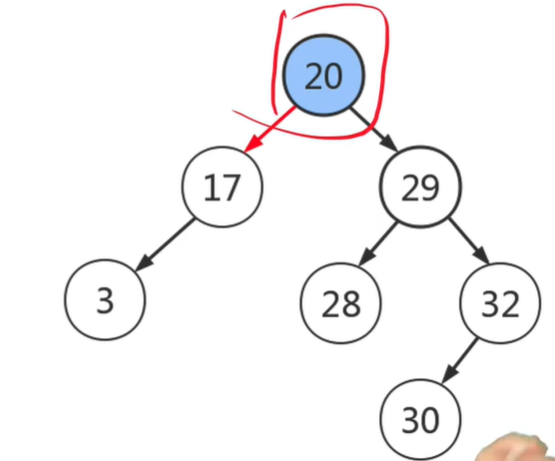
image.png
由性质，10插入到左子树，10 < 17, 10应该是17的左孩子，10 > 3, 10作为3的右孩子
image.png

  • 删除
    • 删除叶子节点 直接删除
    • 删除度为1的节点 删除后，其唯一孩子替换其原来的位置

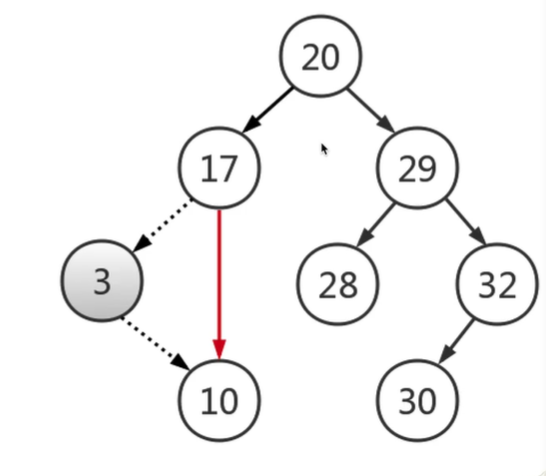
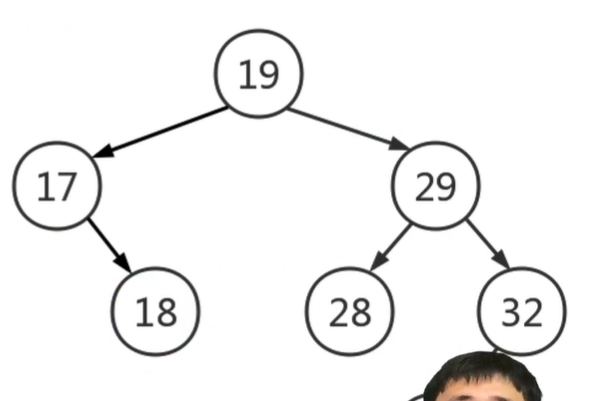
image.png

  • 删除度为2的节点

找到前驱或后继，替换后转换为度为1或叶子节点问题
image.png
image.png
image.png

image.png

  • 课后练习：Leetcode 110 Leetcode 669

小结

二叉排序树

性质

  1. 左子树 < 根节点
  2. 右子树 > 根节点
  3. 中序遍历的结果，是一个有序序列，所以称为二叉排序树

数据结构，就是定义一种性质，并维护这种性质的结构

插入操作

  1. 插入的新节点一定会作为叶子节点存在；

删除操作

  1. 删除度为0的节点，直接删除
  2. 删除度为1的节点，把其子树挂到其父节点上面
  3. 删除度为2的节点，可以转化为删除度为1或度为0的节点

对于度为2的节点：

  1. 前驱：左子树的最大值
  2. 后继：右子树的最小值

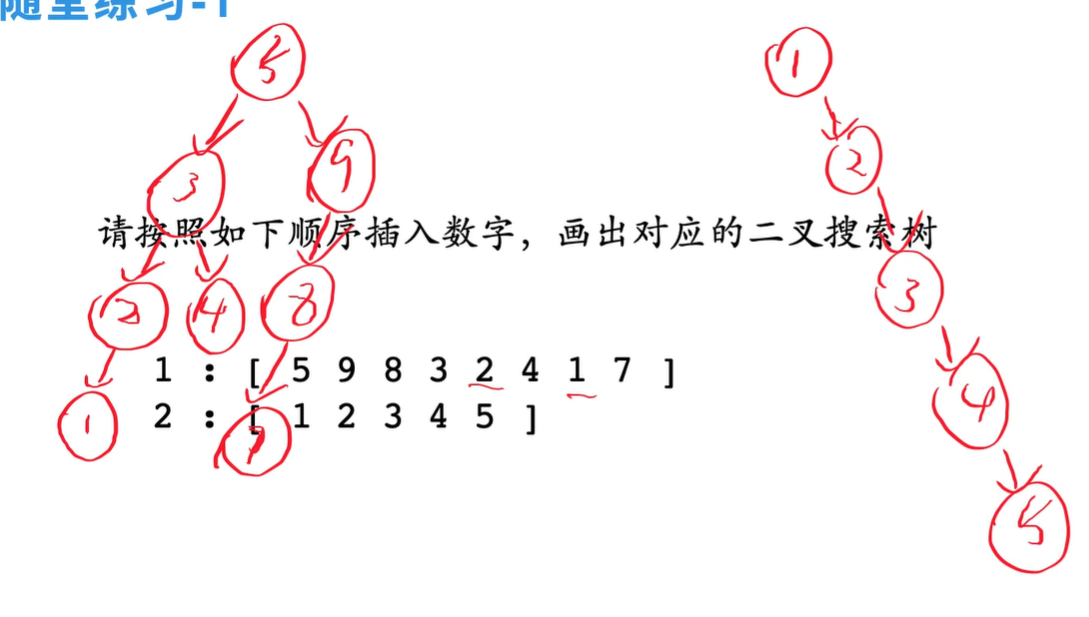
练习

  1. 插入顺序会影响树形结构；
  2. 不同的树形结构，查找效率不同；

平均查找效率：假设每个节点等概率被查找，节点查找次数的期望值，
总次数/总结点数；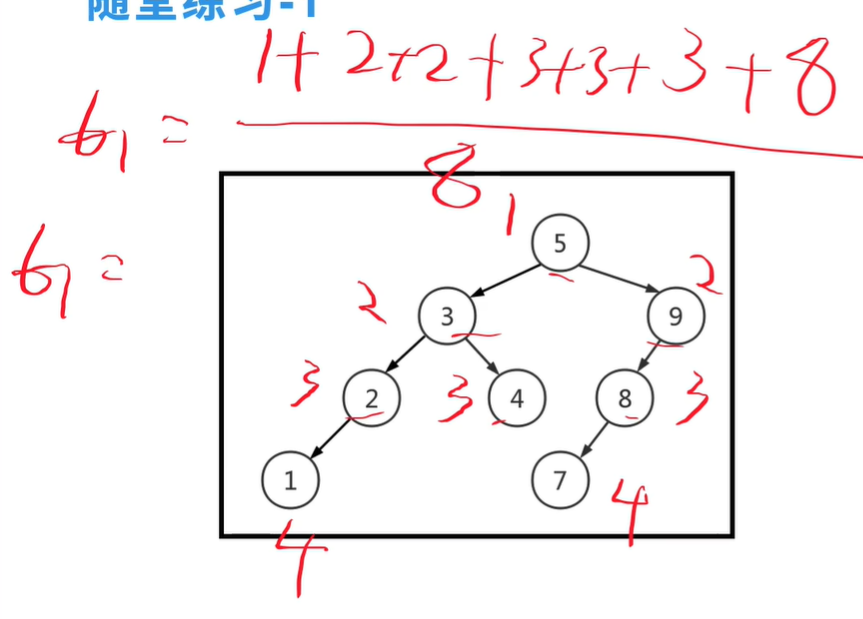
image.png

  1. //file name:
  3. #include <stdio.h>
  4. #include <stdlib.h>
  6. #define KEY(root) (root ? root->key : 0)
  8. typedef struct Node {
  9.     int key;
  10.     struct Node *lchild, *rchild;
  11. } Node;
  13. //新建节点
  14. Node *getNewNode(int val) {
  15.     Node *p = (Node *)malloc(sizeof(Node));
  16.     p->key = val;
  17.     p->lchild = p->rchild = NULL;
  18.     return p;
  19. }
  21. //查找某节点
  22. int search(Node *root, int val) {
  23.     if (root == NULL) return 0;
  24.     if (root->key == val) return 1;
  25.     if (val < root->key) return search(root->lchild, val);  //遍历左子树
  27.     return search(root->rchild, val); //左子树没有，则转向右子树 
  29. }
  31. Node *insert(Node *root, int val) {
  33.     if (root == NULL) return getNewNode(val);   //不存在就新建
  34.     if (root->key == val) return root;          //结点已存在
  36.     if (val < root->key) root->lchild = insert(root->lchild, val); //值小于根节点的值，插入左子树
  37.     else root->rchild = insert(root->rchild, val);                //值大于根结点的值，插入右子树
  38.     return root;
  39. }
  41. //找到结点的前驱
  42. Node *predecessor(Node *root) {
  43.     Node *temp = root->lchild;
  44.     while (temp->rchild) temp = temp->rchild;
  45.     return temp;
  46. }
  48. //删除值为val的结点
  49. Node *erase(Node *root, int val) {
  50.     if (root == NULL) return NULL; //根结点不存在
  51.     if (val < root->key) {        //根节点的值大于要删除的值，走向左子树
  52.         root->lchild = erase(root->lchild, val);
  53.     } else if (val > root->key) {  //根节点的值小于要删除的值，走向右子树
  54.         root->rchild = erase(root->rchild, val);
  55.     } else {                       //要删除的值是根结点的值，即删除度为1的结点，需要找前驱和后继
  56.         if (root->lchild == NULL && root->rchild == NULL) {  //如果无前驱和后继，直接删除
  57.             free(root);
  58.             return NULL;
  59.         } else if (root->lchild == NULL || root->rchild == NULL) {   //前驱和后继有一个不存在
  60.             Node *temp = root->lchild ? root->lchild : root->rchild; //
  61.             free(root);
  62.             return temp;
  63.         } else {
  64.             Node *temp = predecessor(root); //找到前驱
  65.             root->key = temp->key;          //将度为2的结点的值替换为其前驱的值
  66.             root->lchild = erase(root->lchild, temp->key); //删除前驱
  67.         }
  68.     }
  69.     return root;
  70. }
  72. //输出二叉排序树
  73. void output(Node *root) {
  74.     if (root == NULL) return ;
  75.     output(root->lchild);
  76.     printf("%d(%d, %d)\n", KEY(root), KEY(root->lchild), KEY(root->rchild));
  77.     output(root->rchild);
  78.     return ;
  79. }
  81. void post_output(Node *root) {
  82.     if (root == NULL) return ;
  83.     printf("%d(%d, %d)\n", KEY(root), KEY(root->lchild), KEY(root->rchild));
  84.     output(root->lchild);
  85.     output(root->rchild);
  86.     return ;
  87. }
  89. //清除结点
  90. void clear(Node *root) {
  91.     if (root == NULL) return ;
  92.     clear(root->lchild);
  93.     clear(root->rchild);
  94.     free(root);
  95.     return ;
  96. }
  98. int main() {
  99.     int op, val;
  100.     Node *root = NULL;
  101.     while (~scanf("%d%d", &op, &val)) {
  102.         switch(op) {
  103.             case 0: printf("search %d, result = %d\n", val, search(root, val)); break; 
  104.             case 1: root = insert(root, val); break;
  105.             case 2: root = erase(root, val); break;
  106.         }
  107.         if (op){
  108.             output(root);
  109.             printf("--------------------\n");
  110.         }
  111.     }
  112.     printf("-----------------");
  113.     post_output(root);
  114.     printf("===================");
  115.     clear(root);
  116.     return 0;
  117. }

扩展内容

  1. 二叉排序树的删除的优化
  • 删除度为0的结点的操作可以去掉，因为删除度为1的结点的操作也可以删除叶子结点； ```c

    include

    include

define KEY(root) (root ? root->key : 0)

typedef struct Node { int key; struct Node lchild, rchild; } Node;

//新建节点 Node getNewNode(int val) { Node p = (Node *)malloc(sizeof(Node)); p->key = val; p->lchild = p->rchild = NULL; return p; }

//查找某节点 int search(Node *root, int val) { if (root == NULL) return 0; if (root->key == val) return 1; if (val < root->key) return search(root->lchild, val); //遍历左子树

  1. return search(root->rchild, val); //左子树没有，则转向右子树

}

Node insert(Node root, int val) {

if (root == NULL) return getNewNode(val);   //不存在就新建
if (root->key == val) return root;          //结点已存在

if (val < root->key) root->lchild = insert(root->lchild, val); //值小于根节点的值，插入左子树
else root->rchild = insert(root->rchild, val);                //值大于根结点的值，插入右子树
return root;

}

//找到结点的前驱 Node predecessor(Node root) { Node *temp = root->lchild; while (temp->rchild) temp = temp->rchild; return temp; }

//删除值为val的结点 Node erase(Node root, int val) { if (root == NULL) return NULL; //根结点不存在 if (val < root->key) { //根节点的值大于要删除的值，走向左子树 root->lchild = erase(root->lchild, val); } else if (val > root->key) { //根节点的值小于要删除的值，走向右子树 root->rchild = erase(root->rchild, val); } else { //要删除的值是根结点的值，即删除度为1的结点，需要找前驱和后继 // if (root->lchild == NULL && root->rchild == NULL) { //如果无前驱和后继，直接删除 // free(root); // return NULL; // } if (root->lchild == NULL || root->rchild == NULL) { //前驱和后继有一个不存在 Node temp = root->lchild ? root->lchild : root->rchild; // free(root); return temp; } else { Node temp = predecessor(root); //找到前驱 root->key = temp->key; //将度为2的结点的值替换为其前驱的值 root->lchild = erase(root->lchild, temp->key); //删除前驱 } } return root; }

//输出二叉排序树 void output(Node *root) { if (root == NULL) return ; output(root->lchild); printf(“%d(%d, %d)\n”, KEY(root), KEY(root->lchild), KEY(root->rchild)); output(root->rchild); return ; }

void post_output(Node *root) { if (root == NULL) return ; printf(“%d(%d, %d)\n”, KEY(root), KEY(root->lchild), KEY(root->rchild)); output(root->lchild); output(root->rchild); return ; }

//清除结点 void clear(Node *root) { if (root == NULL) return ; clear(root->lchild); clear(root->rchild); free(root); return ; }

int main() { int op, val; Node *root = NULL; while (~scanf(“%d%d”, &op, &val)) { switch(op) { case 0: printf(“search %d, result = %d\n”, val, search(root, val)); break; case 1: root = insert(root, val); break; case 2: root = erase(root, val); break; } if (op){ output(root); printf(“——————————\n”); } } printf(“————————-“); post_output(root); printf(“===================”); clear(root); return 0; } ```

  1. 如何解决排名相关的检索需求
    1. 修改二叉排序树的结构定义，增加一个size字段，记录每棵树的节点数量；
    2. 二叉排序树 - 图9,左子树的结点数量等于k-1，则根节点就是排名第k位的元素；
    3. 二叉排序树 - 图10, 排名第k位的元素在左子树中去找
    4. 二叉排序树 - 图11
  2. 如何解决Top-K问题