B.线性表 - B.3链表 - 《编程基础》

include
include //用于申请动态空间
include

链式存储结构：结点在存储器中的位置是任意的，即逻辑上相邻的数据元素在物理上不一定相邻；
- 线性表的链式表示又称为非顺序映像或链式映像
线性表的链式表示和实现

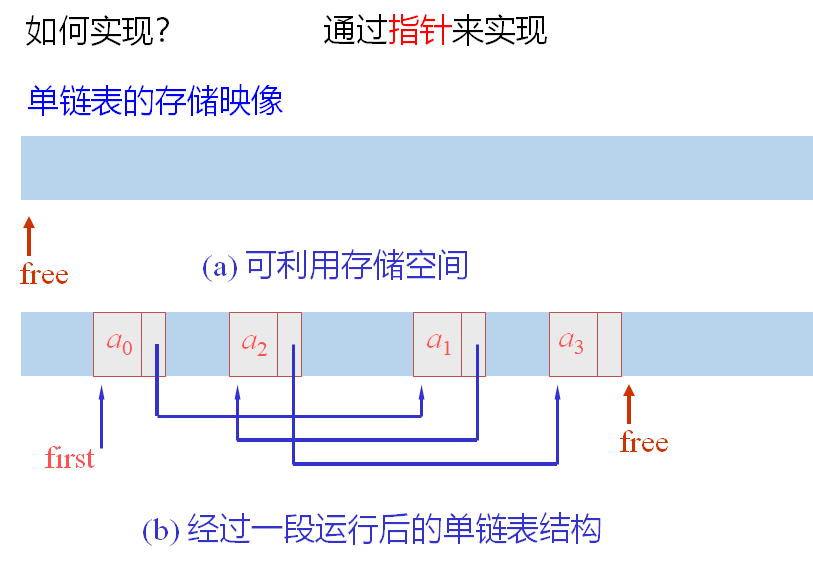
每个数据元素a除了要存储自身的信息外，还需存储一个指示其直接后继的信息，这两部分信息组成数据元素的存储映像，称为结点；
结点包含两个域：
- 存储数据元素信息的数据域；
- 存储后继存储位置的指针域；

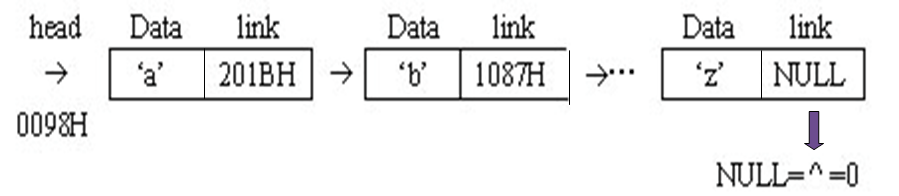
链表： n 个结点由指针链组成一个链表。它是线性表的链式存储映像，称为线性表的链式存储结构。

单链表、双链表、循环链表：
- 结点只有一个指针域的链表，称为单链表或线性链表
- 有两个指针域的链表，称为双链表
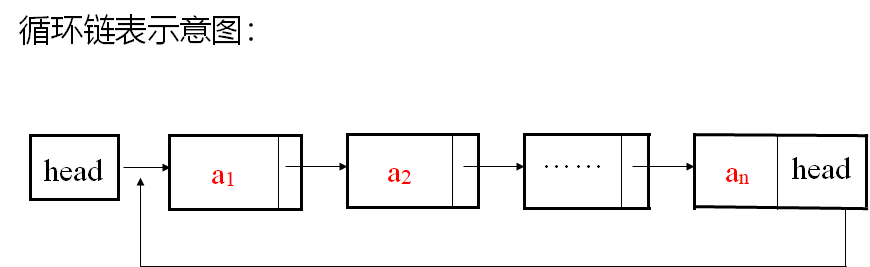
- 首尾相接的链表称为循环链表

链式存储的相关术语

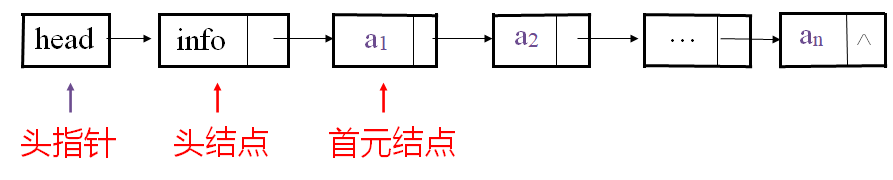
头指针是指向链表中第一个结点的指针
首元结点是指链表中存储第一个数据元素a1的结点
头结点是在链表的首元结点之前附设的一个结点；数据域内只放空表标志和表长等信息

链表的逻辑结构示意图的两种形式：

如何表示空表？

有头结点时，当头结点的指针域为空时表示空表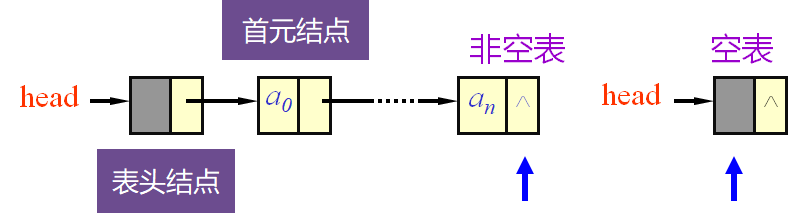

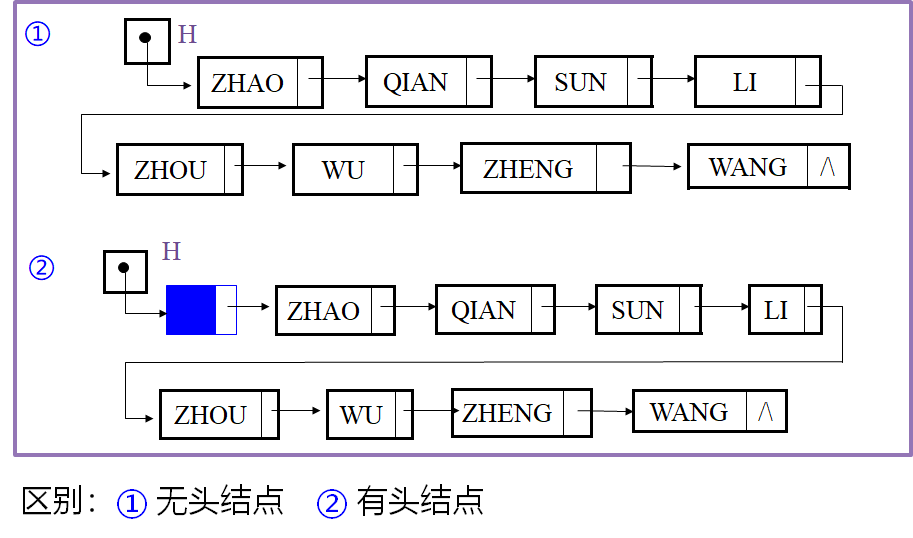
在链表中设置头结点的好处
- 便于首元结点的处理

首元结点的地址保存在头结点的指针域中,所以在链表的第一个位置上的操作和其它位置一致，无须进行特殊处理;

便于空表和非空表的统一处理

无论链表是否为空，头指针都是指向头结点的非空指针，因此空表和非空表的处理也就统一了。

头结点的数据域

头结点的数据域可以为空，也可存放线性表长度等附加信息，但此结点不能计入链表长度值。

链表的特点
- 结点在存储器中的位置是任意的，即逻辑上相邻的数据元素在物理上不一定相邻；
- 访问时只能通过头指针进入链表，并通过每个结点的指针域向后扫描其余结点，所以寻找第一个结点和最后一个结点所花费的时间不等
  - 这种存取元素的方法称为顺序存取法；

链表的优缺点
- 优点
  - 数据元素的个数可以自由扩充
  - 插入、删除等操作不必移动数据，只需修改链接指针，修改效率较高
- 缺点
  - l存储密度小
  - l存取效率不高，必须采用顺序存取，即存取数据元素时，只能按链表的顺序进行访问（顺藤摸瓜）

单链表
- 单链表的定义和实现

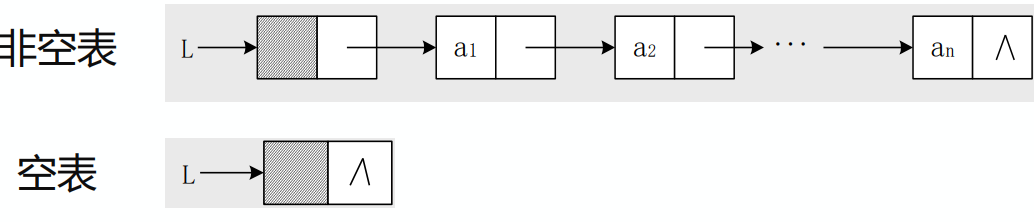
  - 单链表是由表头唯一确定，因此单链表可以用头指针的名字来命名；

单链表的实现

单链表的存储结构定义

typedef struct LNode {
ElemType data;  //数据域
struct LNode *next; //指针域
} LNode, *LinkList;

Linklist与LNode *是等价的，是同一个结构体指针类型的两个名称;
Linklist一般用于定义单链表，如Linklist L，表示指向单链表L的头指针；
用LNode 指向单链表中的某个结点，如LNode p，则p为指向某个结点的指针， *p代表该结点；

与数组名称类似，如果头指针名称为L，则称该链表为表 L；

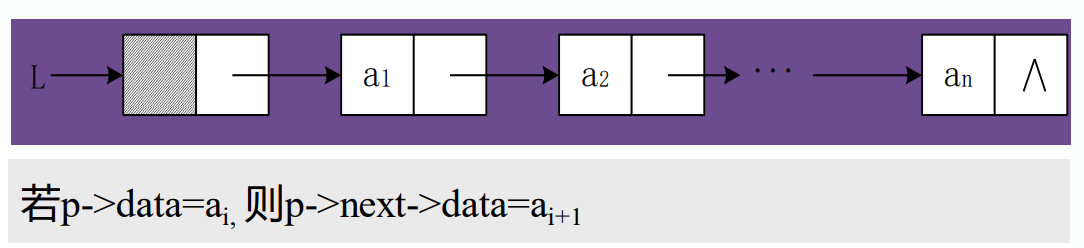
                                                    ![image.png](https://cdn.nlark.com/yuque/0/2021/png/2314091/1620202014088-446d5a24-87d1-4035-babe-d608a05af3b5.png#align=left&display=inline&height=124&margin=%5Bobject%20Object%5D&name=image.png&originHeight=248&originWidth=1084&size=27907&status=done&style=none&width=542)

  - 初始化

                Status InitList_L(LinkList &L) {
                    L = new LNode;
                    L->next = NULL;
                    return OK;
                }

  - 销毁

Status DestroyList_L(LinkList &L) {
    LinkList p;
    while (L) {
        p = L;
        L = L->next;
        delete p;
    }
    return OK;
}

  - 清空

Status ClearList(LinkList &L) {
    LinkList p, q;
    p = L->next;   //p指向第一个结点
    while (p) {  
        q = p->next; 
        delete p; 
        p = q;
    }
    L->next = NULL;
    return OK;
}

  - 求表长

int ListLength_L(LinkList L) {
    LinkList p;
    p = L->next;
    int i = 0;
    while (p) {
        i++;
        p = p->next;
    }
    return i;
}

  - 判断表是否为空

int ListEmpty(LinkList L) {
    if (L->next) return 0;
    else return 1;
}

  - 取值（根据位置i获取相应位置数据元素的内容）

算法步骤：

  1. 从第1个结点顺链扫描，用指针p指向当前扫描到的结点，p初值p=L->next；
  1. j做计数器，累计当前扫描过的结点数，j初值为1；
  1. 当p指向扫描到的下一结点时，计数器j加1；
  1. 当j=i时，p所指的结点就是要找的第i个结点；

Status GetElem_L(LinkList L, int i, ElemType &e) {
    p = L->next;
    int j = 1;
    while (p && j < i) {
        p = p->next;
        ++j;
    }
    if (!p || j > i) return ERROR;
    e = p->data;
    return OK;
}

  - 查找（根据指定数据获取数据所在的位置）

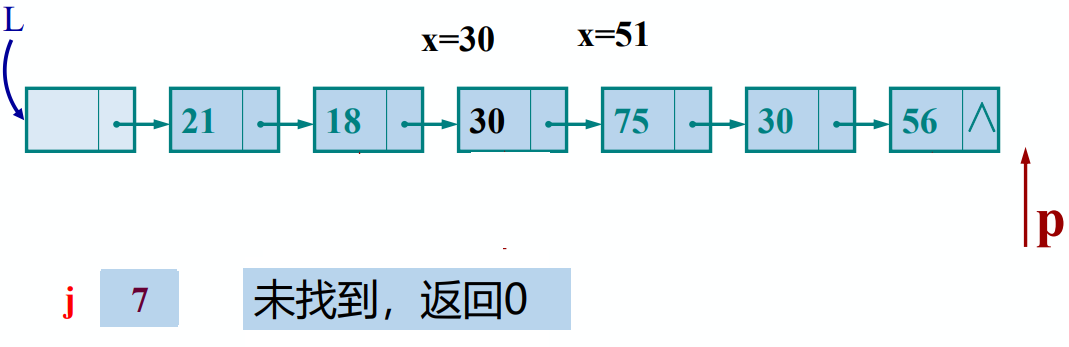
步骤：

  1. 从第一个结点起，依次和e相比较；
  1. 如果找到一个其值与e相等的数据元素，则返回其在链表中的“位置”或地址；
  1. 如果查遍整个链表都没有找到其值和e相等的元素，则返回0或“NULL”

//查找值为e的数据元素，搜索位置
LNode *LocateElem_L(LinkList &L, ElemType e) {
    LinkList p = L->next;
    while (p && p->data != e) p = p->next;
    return p;
}

int LocateElem_L(LinkList L, Elemtype e) {
    p = L->next;
    j = 1;
    while (p && p->data != e) {
        p = p->next;
        j++;
    }
    if (p) return j;
    else return 0;
}

  - 插入（插在第i个结点前）

将值为x的新结点插入到表的第i个结点的位置上，即插入到a与a之间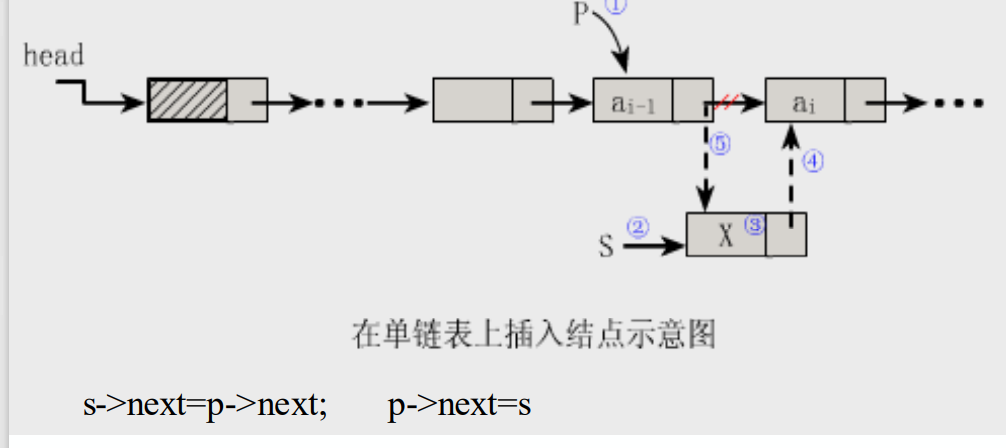

算法步骤：

  1. 找到a的存储位置p；
  1. 生成一个新结点*s；
  1. 将新结点*s的数据置为x；
  1. 新结点*s的指针域指向结点a；
  1. 令结点*p的指针域指向新结点*s

Status ListInsert_L(LinkList &L, int i, ElemType e) {
    p = L; j = 0;
    while (p && j < i - 1) {  //寻找第i-1个结点
        p = p->next;           
        ++j;
    }

    if (!p || j > i - 1) return ERROR;  // i大于表长+1或者小于1
    s = new LNode;                      //生成新结点s
    s->data = e;                        //将结点s的数据域置为e
    s->next = p->next;                    //将结点s插入L中
    p->next = s;
    return OK;
}

  - 删除（删除第i个结点）

步骤：

  1. 找到a存储位置p
  1. 保存要删除的结点的值
  1. 令p->next指向a的直接后继结点
  1. 释放结点a的空间

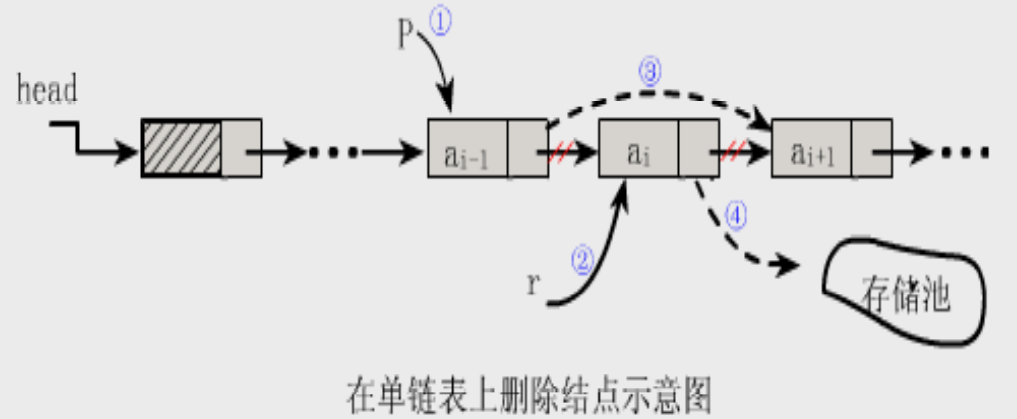
Status ListDelete_L(LinkList &L, int i, ElemType &e) {
    p = L; j = 0;
    while (p->next && j < i - 1) {  //寻找第i个结点，并令p指向其前驱
        p = p->next; ++j;
    }
    if (!(p->next) || j > i - 1) return ERROR; //删除位置不合理
        q = p->next;               //临时保存被删除结点的地址以备释放
        p->next = q->next;             //改变删除结点前驱结点的指针域
        e = q->data;                //保存删除结点的数据域
    delete q;                   //释放删除结点的空间
    return OK;
}

e—————

链表的运算时间效率分析
- 查找：因线性链表只能顺序存取，即在查找时要从头指针找起，查找的时间复杂度为O(n)；
- 插入和删除：因线性链表不需要移动元素，只要修改指针，一般情况下时间复杂度为O(1).但是，如果要在单链表中进行前插或删除操作，由于要从头查找前驱结点，所耗时间复杂度为O(n).

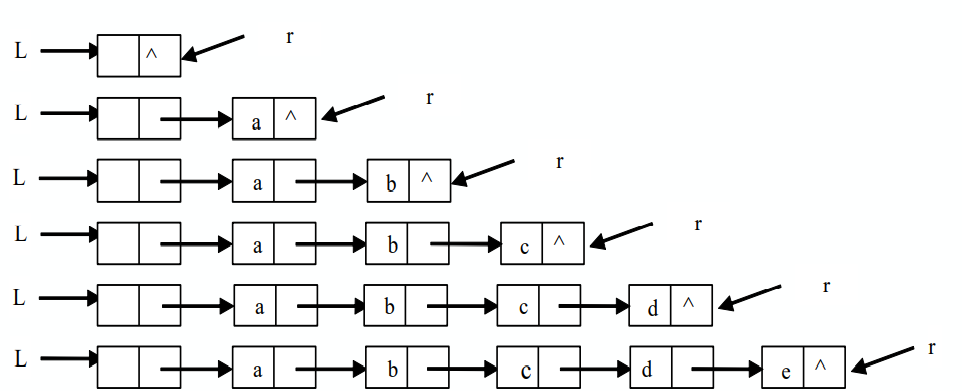
单链表的建立（前插法）
- 从一个空表开始，重复读入数据：
1. 生成新结点；
2. 将读入数据存放到新结点的数据域中；
3. 将该新结点插入到链表的前端；

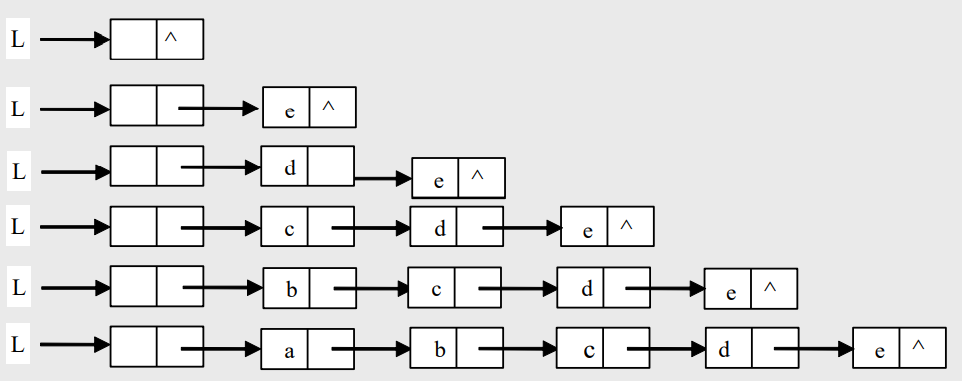
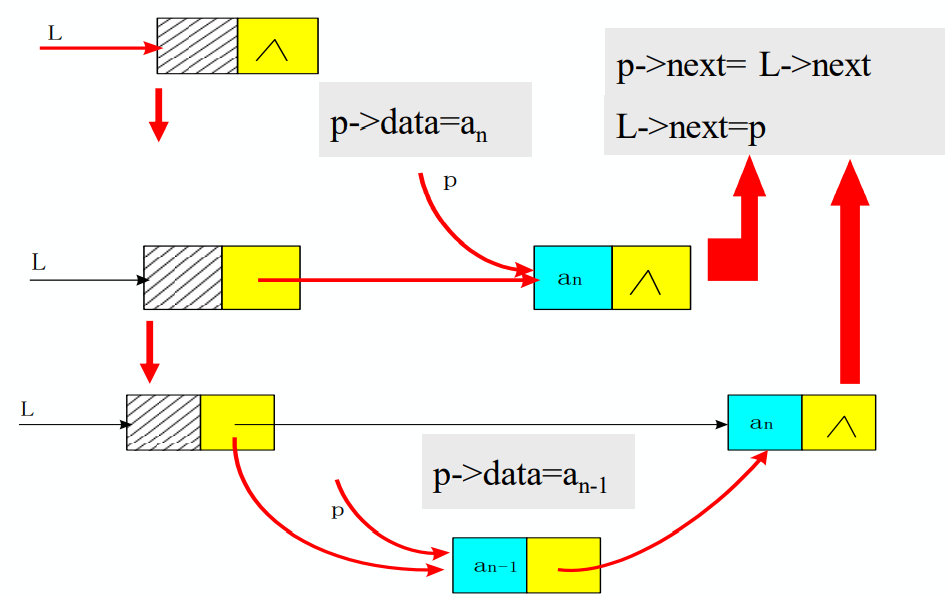
void CreateList_F(LinkList &L, int n) {
    L = new LNode;
    L->next = NULL; //先建立一个带头结点的单链表
    for (i = n; i > 0; --i) {
        p = new LNode; //生成新结点3
        cin >> p->data; //输入元素值
        p->next = L->next;
        L->next = p;   //插入到表头
    }
}

单链表的建立（尾插法）
- 从一个空表L开始，将新结点逐个插入到链表的尾部，尾指针r指向链表的尾结点；
- 初始时，r同L均指向头结点；每读入一个数据元素则申请一个新结点，将新结点插入到尾结点后，r指向新结点；

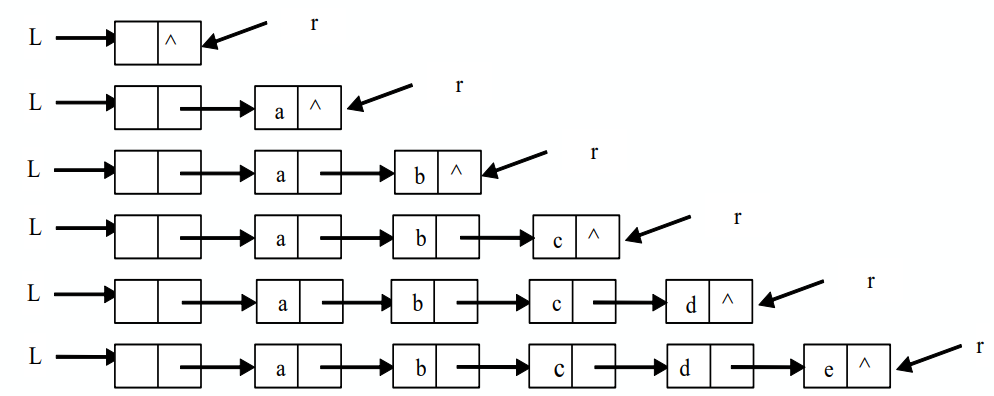
void CreateList_L(LinkList &L, int n) {
    L = new LNode;
    L->next = NULL;
    r = L;
    for (i = 0; i < n; ++i) {
        p = new LNode;   //生成新结点
        cin >> p->data;  //输入元素值
        p->next = NULL; r->next = p; //插入到表尾
        r = p; //r指向新的尾结点
    }
}

循环链表

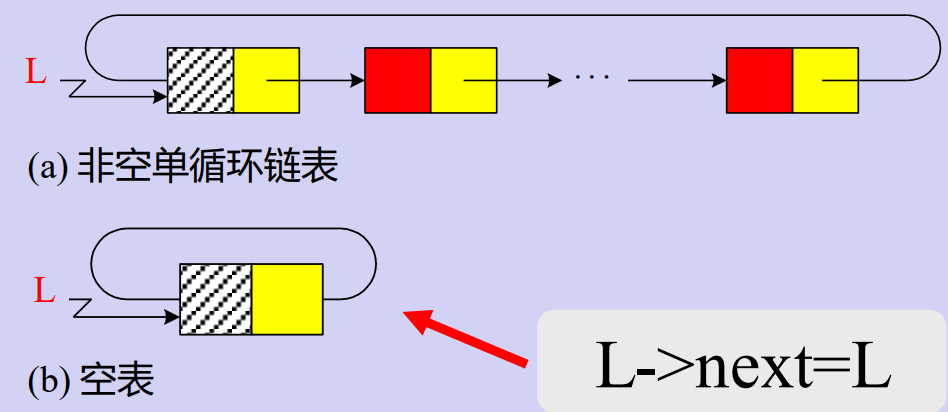
说明：
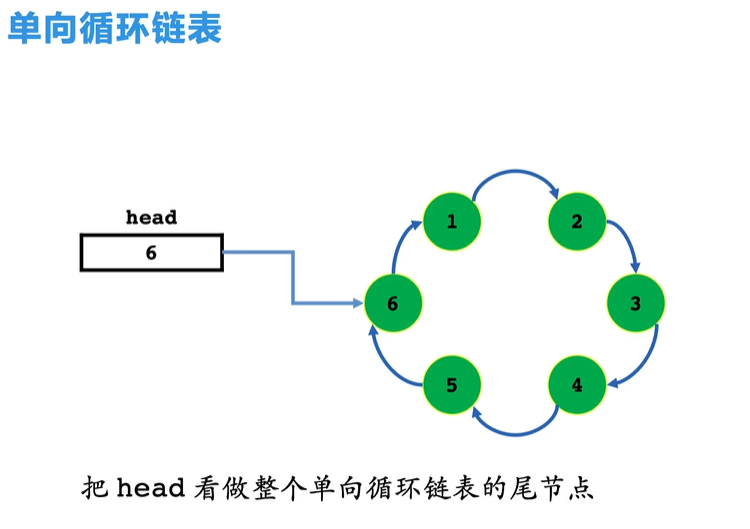
- 从循环链表中的任何一个结点的位置都可以找到其他所有结点，而单链表做不到；
- 循环链表无尾端，如何避免死循环？

循环条件：p != NULL 或 p->next != NULL //单链表
p != L 或 p->next != L //循环链表

  - 对循环链表，有时不给出头指针，而给出尾指针可以更方便的找到第一个和最后一个结点；

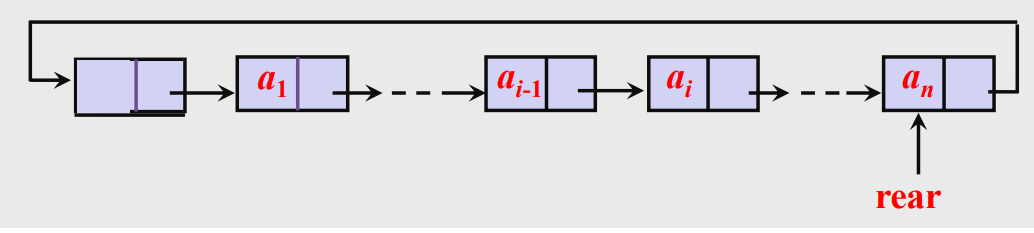                            ![image.png](https://cdn.nlark.com/yuque/0/2021/png/2314091/1620225781230-a456325c-24fa-4f36-91c9-a56a1c3dc016.png#align=left&display=inline&height=117&margin=%5Bobject%20Object%5D&name=image.png&originHeight=233&originWidth=1034&size=17014&status=done&style=none&width=517)<br />如何查找开始结点和终端结点？<br />终端结点：`rear`<br />开始结点：`rear->next->next`

循环链表的合并

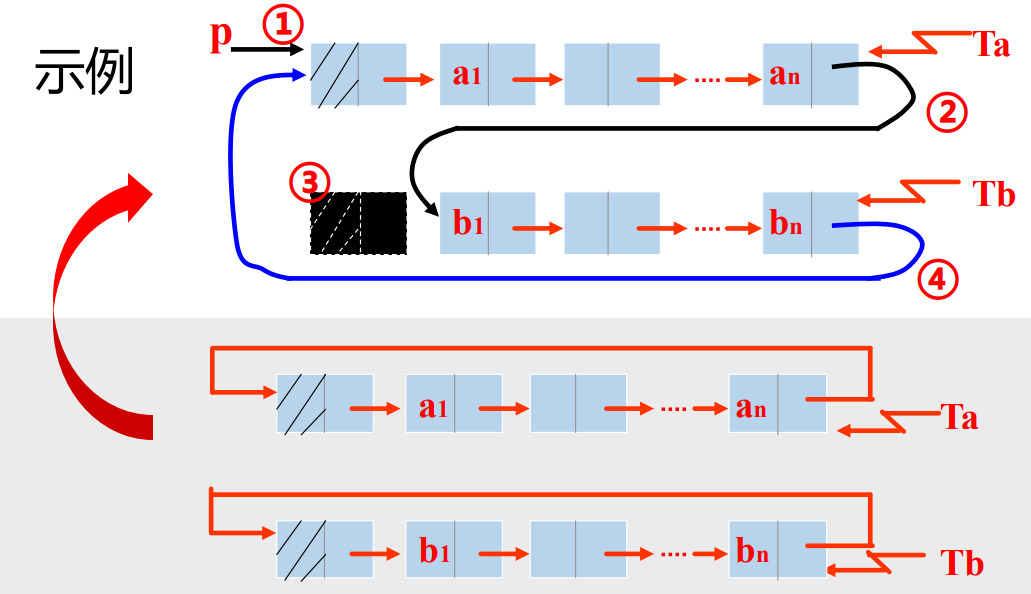
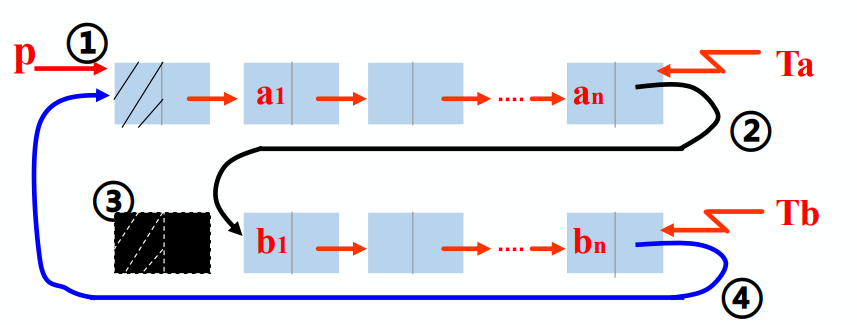
LinkList Connect(LinkList Ta, linkList Tb) {
    p = Ta->next;     //设定p指向Ta的头结点
    Ta->next = Tb->next->next; //Tb表头连结Ta表尾
    delete Tb->next;  //释放Tb表头结点，已经不需要了
    Tb->next = p;     //修改指针
    return Tb;          //新循环单链表的尾结点
}

例：约瑟夫问题

双向链表

typedef struct DuLNode {
    ElemType data;
    struct DuLNode *prior;
    struct DuLNode *next;
} DuLNode, *DuLinkList

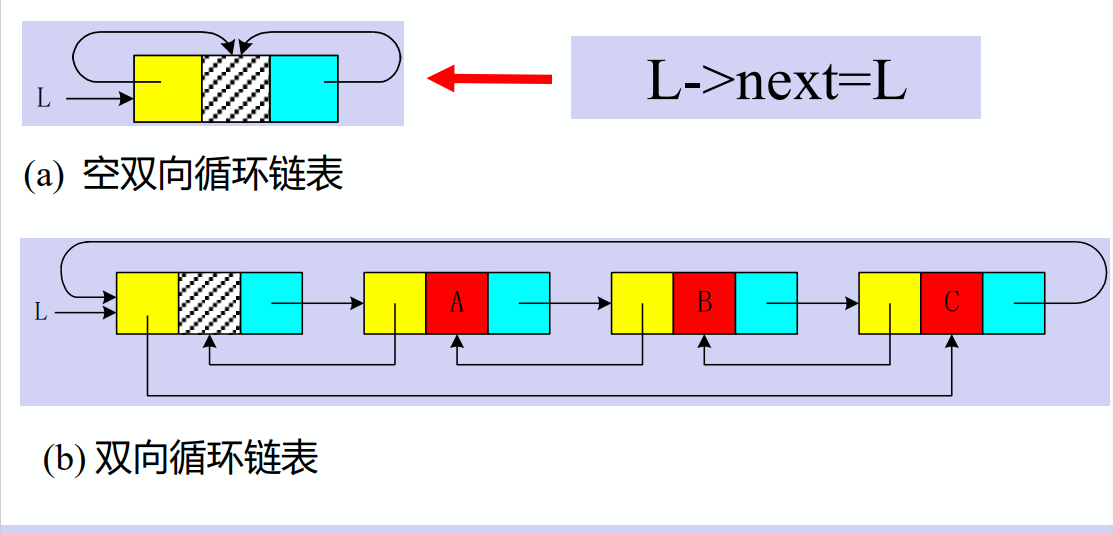
d->next->prior = d->prior->next = d

head称为头指针；

结构操作
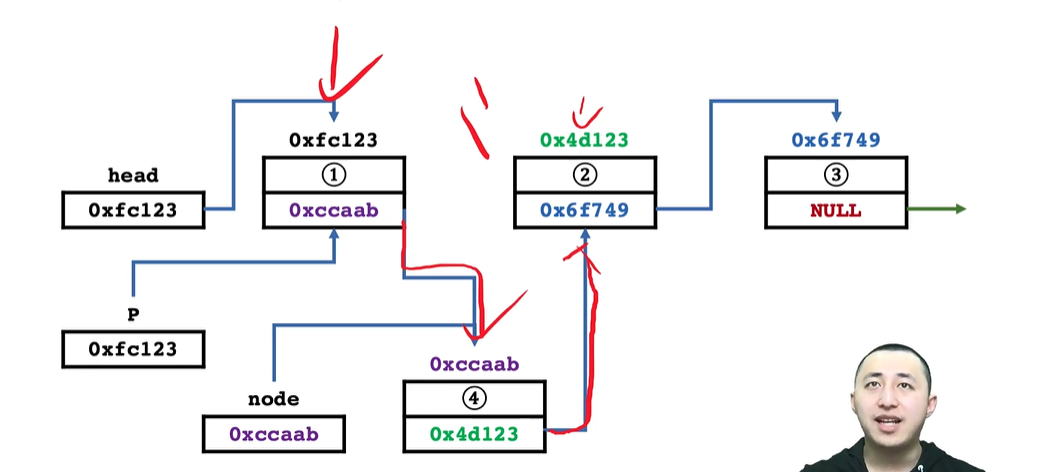
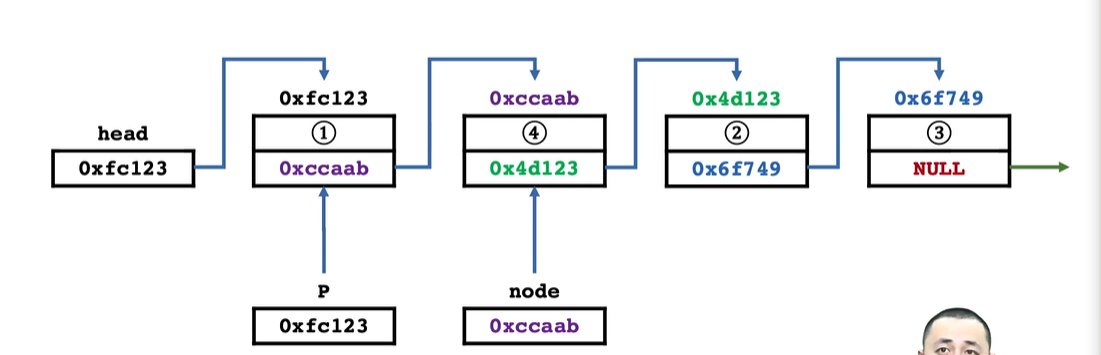
- 插入

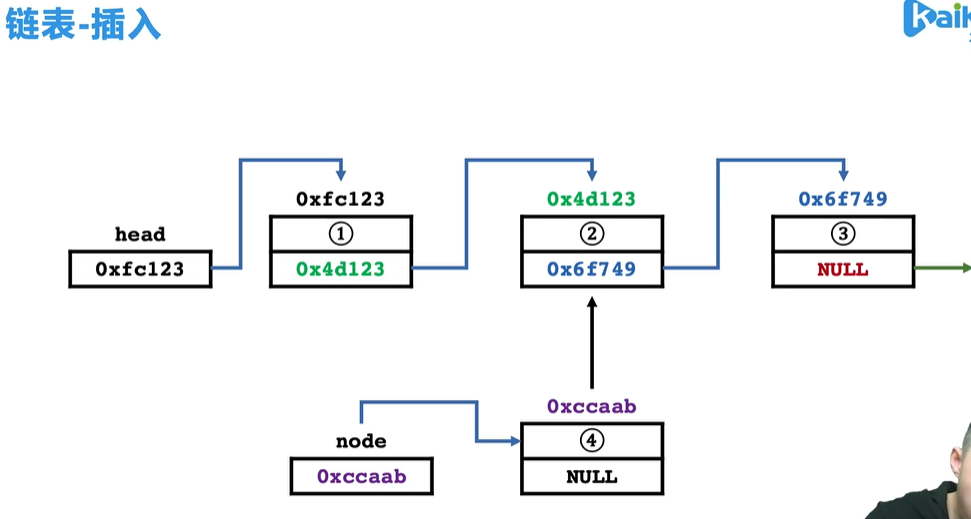
  - 先将待插入节点指向要插入的节点的位置，然后修改前一个元素指向的地址，并指向新插入的地址。

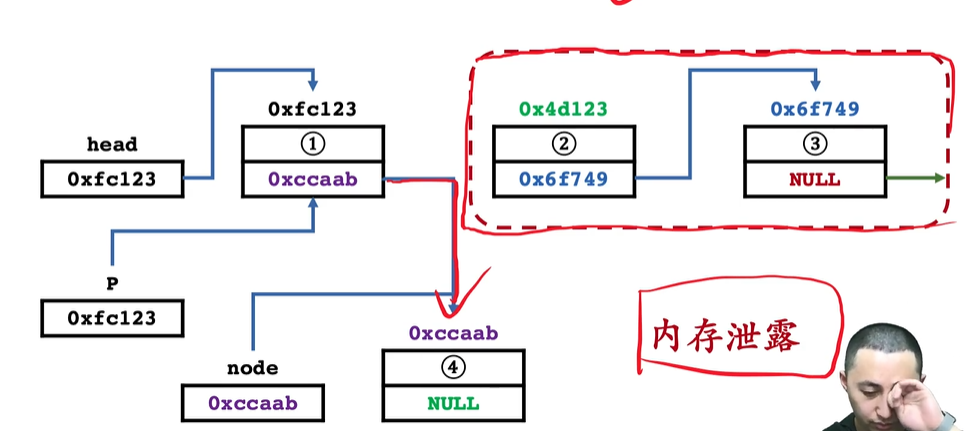
提前断开了要插入位置的元素与前面元素的联系，后面的空间都无法访问，导致内存泄漏。

删除

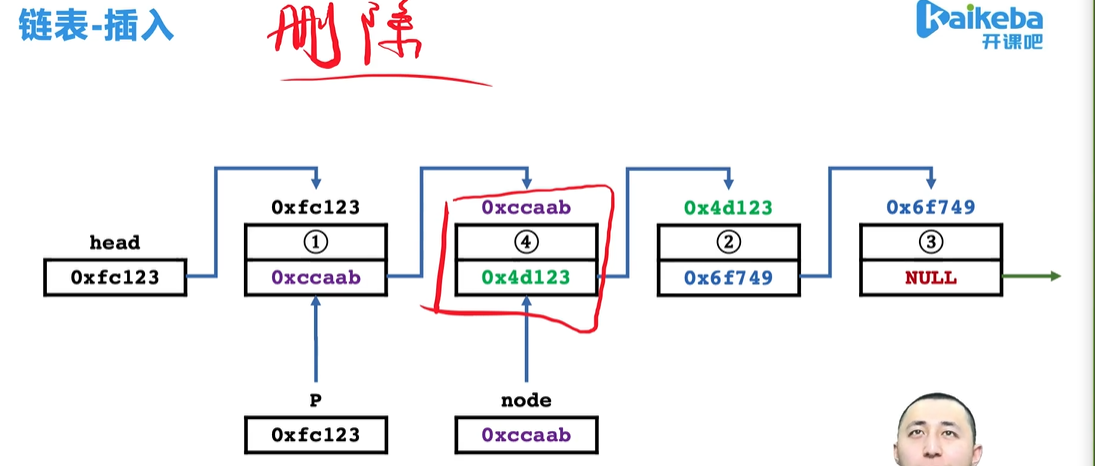
  - 先用一个变量p记录要删除元素的地址，再用一个变量q记录删除元素的前一个元素，把q指向的元素指向要删除元素的后继元素，再释放掉p指向元素所占的空间。

  - 单向循环链表

练习题

代码演示 ```c
include
include //用于申请动态空间
include

//链表的节点定义 typedef struct Node { int data; struct Node *next; } Node;

//链表定义 typedef struct List { //Node *head; //头指针:记录第一个节点的地址，指向头结点或首元结点 Node head;//虚拟头节点（亦简称头结点）作用：数据域不存发数据，仅记录首元结点的地址，能方便插入第一个元素 int length; //当前链表的节点个数 } List;

Node getNewNode(int); List init_List(); void clear_node(Node ); void clear(List ); int inset(List , int, int); int erase(List , int);

//链表节点的初始化 Node getNewNode(int val) { Node p = (Node *)malloc(sizeof(Node)); p->data = val; p->next = NULL; return p; }

//链表的初始化 List init_list() { List l = (List *)malloc(sizeof(List)); l->head.next = NULL; l->length = 0; return l; }

//链表的插入 int insert(List l, int ind, int val) { if (l == NULL) return 0; //若链表创建失败，无法插入 if (ind < 0 || ind > l->length) return 0; //若插入位置超过链表的范围，无法插入；链表的元素下标从0开始，下标是length的位置是链表的最后一位，常为空 Node p = &(l->head), *node = getNewNode(val); //取得虚拟头节点的地址，创建新的节点，传入要插入的数值 while (ind—) p = p->next;//定位到要插入位置的前一个位置 node->next = p->next;//把要插入位置的下一个位置的地址传给要插入的节点 p->next = node;//把插入的元素的地址传给插入位置的前一个元素 l->length += 1;//节点数增加 return 1; }

//链表的删除 int erase(List l, int ind) { if (l == NULL) return 0; if (ind < 0 || ind > l->length) return 0; Node p = &(l->head), *q; while (ind—) p = p->next; q = p->next; p->next = q->next; clear_node(q); l->length -= 1; return 1; }

//链表节点的销毁 void clear_node(Node *node) { if (node == NULL) return; free(node); return ; }

//链表的销毁 void clear(List l) { if (l == NULL) return ; Node p = l->head.next, *q; while (p != NULL) { q = p->next; clear_node(p); p = q; } free(l); return ; }

//链表的反转 void reverse(List l) { //头结点维持在原位置，其后的所有结点倒转 if (l == NULL) return; Node p = l->head.next, *q; //p指向首元结点， l->head.next = NULL;//使首元结点成为新的尾结点 while (p != NULL) { q = p->next; //q指向首元结点的下一位 p->next = l->head.next; //当前p指向的结点的指针域往回指，使自己成为新的首元结点；第一次循环时，p指向的是首元结点，此时，指针域指向NULL，首元结点成为新的尾结点 l->head.next = p; //头结点的指针域存储新的首元结点 p = q; //p指向下一个即将成为首元结点的结点 } return ; }

//链表输出 void output(List l) { if (l == NULL) return ; printf(“list(%d) : “, l->length); for (Node p = l->head.next; p != NULL; p = p->next) { printf(“%d->”, p->data); } printf(“NULL\n”); return ; }

int main() { srand(time(0));

#define MAX_OP 20
List *l = init_list();
for (int i = 0; i < MAX_OP; i++) {
    int op = rand() % 4;
    int val = rand() % 100;
    int ind = rand() % (l->length + 3) - 1;
    switch (op) {
        case 0:
        case 1: {
            printf("insert %d at %d to List = %d\n", val, ind, insert(l, ind, val));
        } break;
        case 2: {
            printf("reverse the List!\n");
            reverse(l);
        } break;
        case 3: {
            printf("erase a item at %d from List = %d\n", ind, erase(l, ind));
        } break;
    }
    output(l), printf("\n");
}   
#undef MAX_OP
clear(l);
return 0;

}



- 单向循环链表

```c
#include <stdio.h>
#include <stdlib.h>

//结点定义
typedef struct Node {
    struct Node *next;
    int data;
} Node;

//链表定义
typedef struct List {
    Node head;
    int length;
} List;

//结点初始化
Node *getnewNode(int val) {
    Node *node = (Node*)malloc(sizeof(Node));
    node->data = val;
    node->next = NULL;
    return node;
}

//链表初始化
List *init_List() {
    List *l = (List*)malloc(sizeof(List));
    l->head.next = &(l->head); //构成循环链表
    l->length = 0;
    return l;
}


//插入：插入位置是ind
int insert(List *l, int val, int ind) { //！！！ind是待插入元素在链表中的序号，序号从0开始！！！
    if (l ==NULL) return 0;
    if (ind < 0 || ind > l->length) return 0; 
    Node *p = &(l->head), *q;
    while (ind--) p = p->next; //递进ind次
    q = getnewNode(val);
    q->next = p->next;
    p->next = q;
    l->length += 1;    
    return 1;
}


void clear_node(Node *p) {
    if (p == NULL) return ;
    free(p);
    return ;
}



void clear(List *l) {
    if (l == NULL) return ;
    Node *p = l->head.next, *q;
    while (p != &(l->head)) { //循环链表的终止条件是碰到头结点
        q = p->next;
        clear_node(p);
        p = q;
    }
    free(l);
    return ;
}


void output(List *l) {
    if (l == NULL) return ;
    printf("list(%d) : ", l->length);
    for (Node *p = l->head.next; p != &(l->head); p = p->next) {
        printf("%d->", p->data);
    }
    printf("NULL\n");
    return ;
}

int main() {
    #define MAX_N 10005

    int N, M;
    List *l = init_List();
    scanf("%d %d", &N, &M);
    int a[MAX_N] = {0};
    int m = M % N;
    if (m == 1) { 
        for (int i = 0; i < N; i++) {
            printf("%d ", i + 1);
        }
    }
    for (int i = 0; i < N; i++) {
        insert(l, i + 1,i);
    }
    output(l);
    clear(l);
    return 0;
}

双向链表

前驱指针pre
后继指针next

线性结构：存在唯一的指向关系

链表不支持随机访问，要访问某个值需要从前往后遍历。
顺序表支持随机访问

作业：
OJ提高组#272

B.3链表

include

include //用于申请动态空间

include