最近在看论文的时候遇到了对极几何这个知识点，之前完全没有听到过，这里做一个补充学习。

什么是对极几何

如果仅看一个相机，我们并不能知道深度信息，可如果有两个相机的话（就像人有两只眼睛）我们就能得到深度的信息，用两个相机在不同的位置拍摄同一物体，如果两张照片中的景物有重叠的部分，我们有理由相信，这两张照片之间存在一定的对应关系，

所以要想获得二位图片的深度信息，需要通过两张及以上的图片进行多幅图片中对应点的匹配，然后通过一种方法进行计算深度得到，其中一种描述多视角图片深度关系的方法就是对极几何。

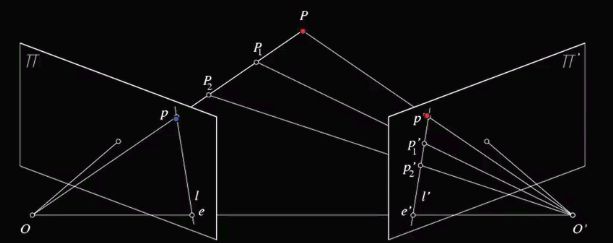
上图O和O’是两个相机中心，P点是物体所在，如果我们只看左边图像 上的点p，我们不能知道物体到底是在哪，点P1、P2或其他地方，可有了右边图像 上的p’我们就能得到物体点P

在上图，我们把两相机中心的连线OO’成为基线，把他们与观测物体的平面OO’P成为对极平面，对极平面与两相机图像的交线l和l’称为对极线，而OO’与两图像的交点e,e’就是对极点。

本质矩阵(Essential Matrix)

对于如图所示，P是物体在世界坐标中的位置，p(后文中直接称为P)和p’（后文中称为P’）分别是P在两个相机成像平面上的投影，O为相机1的光心，O’为相机2的光心，从p到p’为刚体运动，转换公式为：

P’实际上是OP’向量，而T是O’T向量，而这两个向量都位于OO’P这个对极平面上，因此两个向量的叉乘即为对极平面的法向量：

因为T*T=0，所以最后，再左乘P’,P’与法向量垂直，因此可得：

两向量的叉乘可以转换为一向量的反对称矩阵与另一向量的点乘，由此可得：

有些作者将
设本质矩阵为E，得：

即：

由上可知，约束两个成像点关系的，就只有T和R这个内参数

基本矩阵(Fundamental Matrix)

还记得我们将世界坐标系的观测点转换到2D图像点的方法吗，没错，就是用相机矩阵，而相机矩阵又分为内参和外参的，代数表示为
K和 分别表示内参矩阵和外参矩阵，P_im和P_w分别表示图像点和世界点，如果我们把经外参矩阵转换到相机坐标系的世界点称作P_c，那么上式可化为
现在我们考虑左右两视图，又由于K是可逆的，有
还记得上面的本质矩阵吗

将矩阵相乘

我们另 ,上式化简为

而F就是我们的基本矩阵
**
关于F与E的关系：

即

本质矩阵求解相机运动

在实际中我们可以通过特征点匹配（如ORBSLAM2使用ORB特征）计算出相机运动前后两幅视图中较多组匹配特征点坐标 与 ，另外相机内参矩阵 已知。

通过对极几何恢复相机运动的过程为：特征点匹配 → 计算本质矩阵 → 恢复相机运动。
以本质矩阵 的定义公式来看，两边乘以 ，得：

化简得

再回头来看公式 ：

其中 且 ，带表相机主点位置。这时明显可以看到findEssentialMat代码通过上述过程计算本质矩阵 。

• 奇异值分解 计算相机运动

对 进行初等行变换：

这里的 是一个正交矩阵（ ）。通过上述初等行变换可以得到：

那么通过公式 改写 为：

同理通过公式 改写 为：

观察公式 和 ，这就是典型的奇异值分解（SVD）：

其中 和 都是正交矩阵， 且 。同时可以得到结论：

一个矩阵是本质矩阵的充要条件是其奇异值中有两个相等且第三个是0。

那么看到这儿应该比较清晰了，通过两幅图对极几何计算相机运动的方法是：

1. 特征点匹配计算 和
2. 通过对极约束 计算本质矩阵
3. 用奇异值分解 计算 和 ，从而得到旋转矩阵 和平移向量

• 机运动 和 的四个解

已知 并进行奇异值分解(SVD)求得 和 之后，那么根据公式 和 可以得到旋转矩阵的两个解：

接着可以得到：

对于对极约束 ，两边乘以 等式依然成立；对本质矩阵的数值解来说， 和 只是相差一个负号；但是对于平移向量， 和 代表方向相反。

综合考虑，求解得到的 和 共有4种如下可能位置：

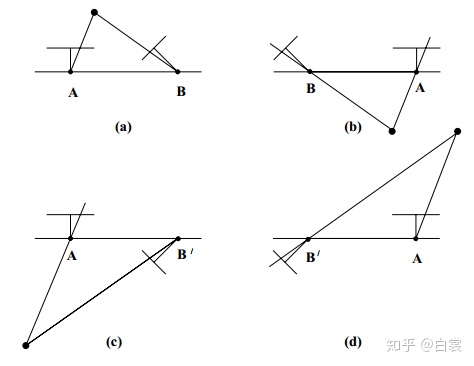
由于真实物理条件限定，两个相机和被拍摄点在同一侧，且被拍摄点在相机前方，所以只有上图中(a)是符合真实的解。

在OpenCV中cv::recoverPose函数帮我们做这一堆事情

输入本质矩阵、匹配特征点 _points1 + _points2、相机矩阵 _cameraMatrix，输出旋转矩阵 _R和平移向量 _t 。代码太长就不列出来了。

若干问题

• 对极几何不能求解纯旋转问题

当相机无平移且只有旋转时 为全 矩阵，等式两边都等于 显然会导致无法求解 。反过来当相机只有平移且无旋转时 ，并不影响 的求解，这时问题退化成双目测距。

• 对极几何“结构性”恢复运动

对于对极约束 ，在等式两边乘以任意不为 的常数 都成立：

换句话说，如果 是 的解，那么 也是 的解。
这就是说，即使求解出平移向量 ，我们也无法知道 的单位具体是米、厘米还是毫米。所以计出的 只是恢复移动的“结构性”，并不是真实值。

ref

https://zhuanlan.zhihu.com/p/141799551
https://www.cnblogs.com/gemstone/articles/2294551.html
https://zhuanlan.zhihu.com/p/33458436