为什么需要复杂度分析？

事后统计法:

  • 测试结果非常依赖测试环境
  • 测试结果受数据规模的影响很大

大 O 复杂度表示法

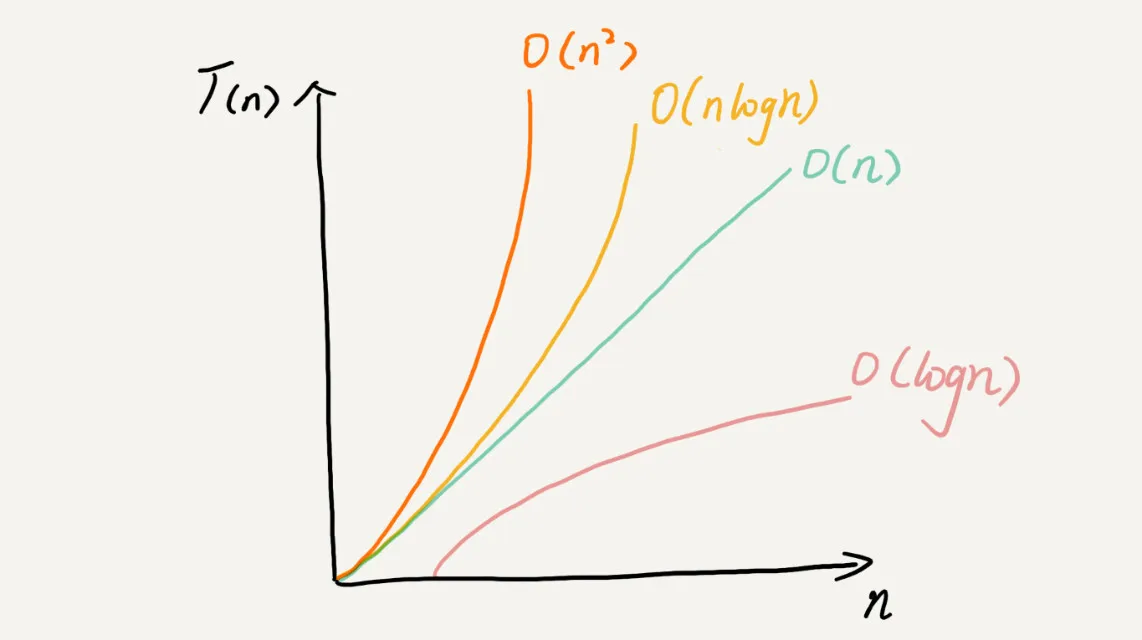
所有代码的执行时间 T(n) 与每行代码的执行次数 f(n) 成正比。

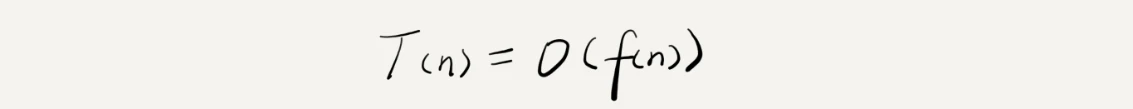
image.png

渐进时间复杂度（asymptotic time complexity），简称时间复杂度

时间复杂度分析

  • 只关注循环执行次数最多的一段代码
  1.  int cal(int n) {
  2.    int sum = 0;
  3.    int i = 1;
  4.    for (; i <= n; ++i) {
  5.      sum = sum + i;
  6.    }
  7.    return sum;
  8.  }
  • 加法法则：总复杂度等于量级最大的那段代码的复杂度
  1. int cal(int n) {
  2.    int sum_1 = 0;
  3.    int p = 1;
  4.    for (; p < 100; ++p) {
  5.      sum_1 = sum_1 + p;
  6.    }
  8.    int sum_2 = 0;
  9.    int q = 1;
  10.    for (; q < n; ++q) {
  11.      sum_2 = sum_2 + q;
  12.    }
  14.    int sum_3 = 0;
  15.    int i = 1;
  16.    int j = 1;
  17.    for (; i <= n; ++i) {
  18.      j = 1; 
  19.      for (; j <= n; ++j) {
  20.        sum_3 = sum_3 +  i * j;
  21.      }
  22.    }
  24.    return sum_1 + sum_2 + sum_3;
  25.  }
  • 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
  1. int cal(int n) {
  2.    int ret = 0; 
  3.    int i = 1;
  4.    for (; i < n; ++i) {
  5.      ret = ret + f(i);
  6.    } 
  7.  } 
  9.  int f(int n) {
  10.   int sum = 0;
  11.   int i = 1;
  12.   for (; i < n; ++i) {
  13.     sum = sum + i;
  14.   } 
  15.   return sum;
  16.  }

几种常见时间复杂度实例分析

image.png

O(1)

  1.  int i = 8;
  2.  int j = 6;
  3.  int sum = i + j;

O(logn)、O(nlogn)

  1.  i=1;
  2.  while (i <= n)  {
  3.    i = i * 2;
  4.  }

image.png

  1.  i=1;
  2.  while (i <= n)  {
  3.    i = i * 3;
  4.  }

O(m+n)、O(m*n)

  1. int cal(int m, int n) {
  2.   int sum_1 = 0;
  3.   int i = 1;
  4.   for (; i < m; ++i) {
  5.     sum_1 = sum_1 + i;
  6.   }
  8.   int sum_2 = 0;
  9.   int j = 1;
  10.   for (; j < n; ++j) {
  11.     sum_2 = sum_2 + j;
  12.   }
  14.   return sum_1 + sum_2;
  15. }

空间复杂度分析

渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系

  1. void print(int n) {
  2.   int i = 0;
  3.   int[] a = new int[n]; // O(n)
  4.   for (i; i <n; ++i) {
  5.     a[i] = i * i;
  6.   }
  8.   for (i = n-1; i >= 0; --i) {
  9.     print out a[i]
  10.   }
  11. }

内容小结

image.png