大 O 复杂度表示法

复杂度: T(n)=(2n+2)*unit_time 

  1. int cal(int n) {
  2.   int sum = 0;
  3.   int i = 1;
  4.   for (; i <= n; ++i) {
  5.     sum = sum + i;
  6.   }
  7.   return sum;
  8. }

复杂度: T(n)=(2n+2n+3)*unit_time 

  1. int cal(int n) {
  2.   int sum = 0;
  3.   int i = 1;
  4.   int j = 1;
  5.   for (; i <= n; ++i) {
  6.     j = 1;
  7.     for (; j <= n; ++j) {
  8.       sum = sum +  i * j;
  9.     }
  10.   }
  11. }

公式总结:

复杂度分析 - 图1

可以只记录最大的数量级: T(n)=O(n) , T(n)=O(n)

大 O 表示法不是真正的执行时间, 而是表示代码执行时间随数据规模增长的变化趋势, 所以也叫作渐进时间复杂度, 简称时间复杂度.

分析时间复杂度的方法

  • 只关注循环执行次数最多的一段代码
  • 加法法则: 总复杂度等于量级最大的那段代码的复杂度
  • 乘法法则: 嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

几种常见时间复杂度实例分析

非多项式量级 (NP, Non-Deterministic Polynomial, 非确定多项式) (递增):

  • 指数阶 O(2)
  • 阶乘阶 O(n!)

多项式时间复杂度 (递增):

  • 常量阶 O(1)
  • 对数阶 O(logn)
  • 线性阶 O(n)
  • 线性对数阶 O(nlogn)
  • 平方阶 O(n) 立方阶 O(n) k 次方阶 O(n)

O(1)

不是指只运行一行代码, 而是代码执行时间不随 n 的增大而增长.

  1. int i = 8;
  2. int j = 6;
  3. int sum = i + j;

O(logn) , O(nlogn)

这段代码的复杂度是第3行的执行次数, 而该行的执行次数为 x=logn , 所以复杂度为 O(logn) 

  1. i=1;
  2. while (i <= n)  {
  3.   i = i * 2;
  4. }

同理, 以下例子的复杂度为 O(logn) 

  1. i=1;
  2. while (i <= n)  {
  3.   i = i * 3;
  4. }

O(nlogn) 其实是 n 次 logn

O(m+n) , O(m*n)

不能简单的利用加法法则来忽略其中一个:

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

空间复杂度分析

渐进空间复杂度.

空间复杂度为 O(n) :

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

各复杂度图示

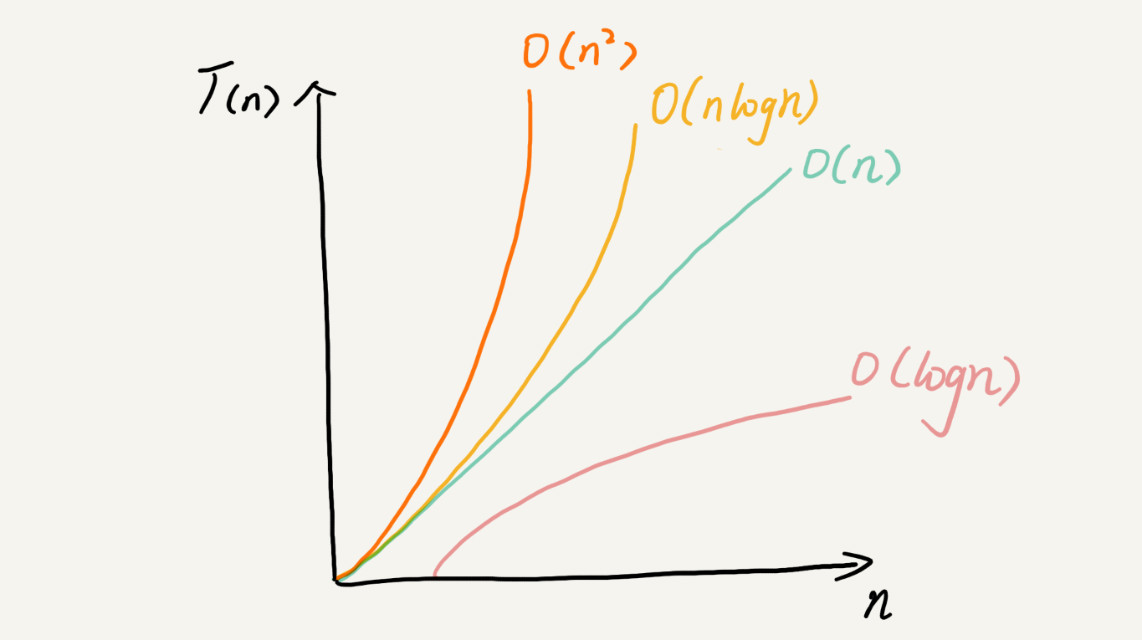
image.png

最好, 最坏情况时间复杂度

复杂度为 O(n) :

// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) pos = i; // 注意这里并没有直接返回
  }
  return pos;
}

优化后的时间复杂度没那么简单:

  • 最好
  • 最坏
// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
       pos = i;
       break; // 找到后就退出
    }
  }
  return pos;
}

平均情况时间复杂度

上面例子中, 有 n+1 种情况: 在数组中和不在数组中, 计算它的平均复杂度就是将每种情况相加, 再除以 n+1 :

复杂度分析 - 图3

这个式子可以看成复杂度为 O(n) . 但是这个推理过程没有考虑出现概率. 如果目标在或不在数组中的概率各为 1/2 , 在数组中的位置出现的概率为 1/2n , 那么平均出现的次数相当于计算加权平均值, 也叫作期望值:

复杂度分析 - 图4

复杂度仍为 O(n) .

均摊时间复杂度

使用摊还分析.

// array表示一个长度为n的数组
// 代码中的array.length就等于n
int[] array = new int[n];
int count = 0;

void insert(int val) {
   if (count == array.length) {
      int sum = 0;
      for (int i = 0; i < array.length; ++i) {
         sum = sum + array[i];
      }
      array[0] = sum;
      count = 1;
   }

    array[count] = val;
   ++count;
}
  • 最好时的复杂度为 O(1)
  • 最坏时的复杂度为 O(n)
  • 平均时间复杂度为 O(1)

上面例子中, 一共有 n+1 种情况: 数组不满和数组满, 它们的出现概率是相等的 1/(n+1) . 复杂度计算就是计算其加权平均值:

复杂度分析 - 图5

前面有 n 个 1*1/(n+1) , 后跟一个统计 sum 的 n 次遍历. 从规律的角度来看, 每有一次 O(n) 的插入 (求和), 后面都会跟着 O(1) 的插入操作, 然后均摊.