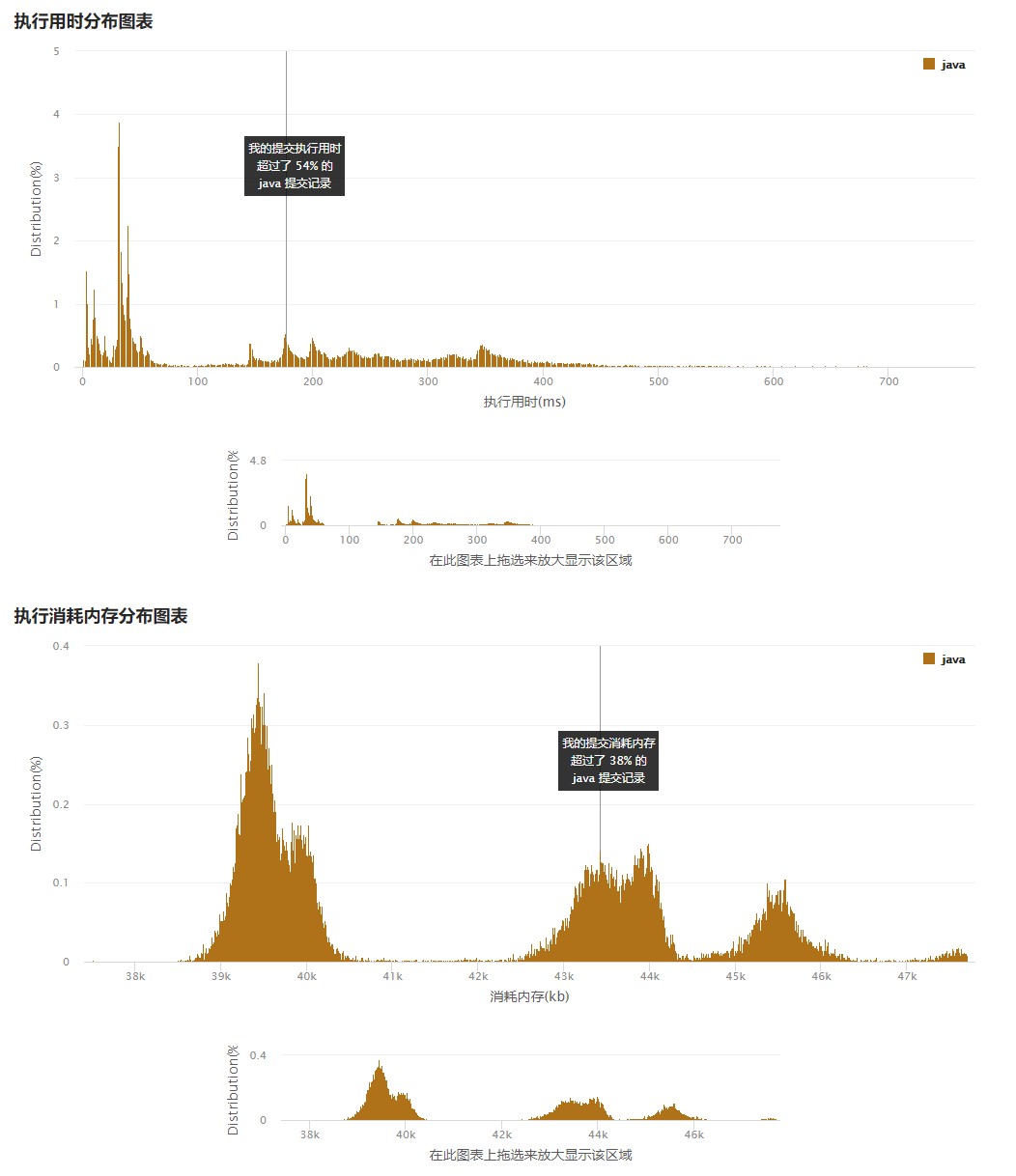
题目

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：
输入：s = “cbbd”
输出：“bb”

示例 3：
输入：s = “a”
输出：“a”

示例 4：
输入：s = “ac”
输出：“a”


提示：

  • 1 <= s.length <= 1000
  • s 仅由数字和英文字母（大写和/或小写）组成

解题思路

1、枚举所有的子串（暴力搜索）

枚举出所有的子串，然后判断是否为回文串。
时间复杂度：O(n³) ，这里 n 为字符串的长度；
空间复杂度：O(1)，只用到常数个临时变量。

2、枚举所有可能的回文子串的中心位置（暴力搜索/中心扩展）

枚举所有的「回文中心」并尝试「扩展」，直到无法扩展为止，此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值，即可得到最终的答案。

枚举时需要考虑回文字符串长度的奇偶性
image.png

时间复杂度：O(n²)，枚举中心位置的个数是 2(n-1)，每一次向两边扩散检测是否为回文；
空间复杂度：O(1)，只用到常数个临时变量。

3、动态规划

动态规划实际上是在填写一张二维表格。

回文串是天然具有状态转移性质的，一个回文去掉两头以后，剩下的部分仍然是回文。当然，这里说的回文长度严格大于 2 。

如果一个子串的两头不相等，那么可以直接下结论，该子串不是回文。例如：
image.png

如果一个子串首尾两个字符相等，要看去掉首尾两个字符的部分是不是回文。

状态：dp[ i ][ j ] 表示子串 s [ i..j ] 是否为回文子串（ s[ i ] 和 s[ j ] 都是可以取到的）。
得到状态转移方程：dp[ i ][ j ] = ( s[ i ]==s[ j ] ) and dp[ i+1 ][ j-1 ]

既然是下标访问，就要考虑到下标边界。
边界条件：j - 1 - ( i + 1 ) + 1 < 2 ，整理后得到 j - i < 3 等价于 j - i + 1 < 4 ，其语义是 s [ i..j ] 长度为 2 或 3 时，不用检查子串是否为回文，这个时候不需要状态转移。

如果 j - 1 到 i + 1 长度小于2，不构成区间的的话 dp[ i+1 ][ j-1 ] 没有意义

说到这里你应该也明白了，动态规划比枚举快就快在：借助状态转移方程，每一步的计算都尽可能的利用了上一步计算的结果，这是非常典型的空间换时间的算法思想。

下面我们考虑初始化条件，单个字符一定是回文串，因此对角线的值可以先赋值为 true 。
初始化：dp[ i ][ j ] = true

事实上，初始化的部分是可以省略的，因为我们真正执行一下代码就会发现，对角线上的数值是不会被其他状态值参考的。

下面我们考虑输出，我们在填表的时候只要得到一个状态值为 true 的时候，就记录此时回文子串的起始位置和长度，填表完成以后再截取。
输出：在得到一个状态的值为 true 的时候，记录起始位置和长度，填表完成以后再截取。

最后，回过头来看一下，因为有下标边界的限制，所以对于状态转移方程需要做进一步的修改
原始：dp[ i ][ j ] = ( s[ i ]==s[ j ] ) and dp[ i+1 ][ j-1 ]
改为：dp[ i ][ j ] = ( s[ i ]==s[ j ] ) and ( j - i < 3 or dp[ i+1 ][ j-1 ] )

其语义为：子串是否为回文取决于：在子串首尾两个字符相等的情况下，如果 j - 1 到 i + 1 长度大等于2，构成区间，再根据去掉首尾两个字符后的子串是否为回文串决定原始子串是否为回文。

再重申一遍，动态规划实际上是在填写一张二维表格。
由于 i 和 j 的关系是 i <= j ，所以我们只要填写表格的上半部分。
image.png

这个二维表格就记录了我们求解 s 的所有子串问题的所有状态，每一行表示 s 的左边界 ，每一列表示 s 的右边界。左边界和右边界的组合就确定了一个唯一的子串。

首先，单个字符一定是回文串，所以我们可以先对主角线位置的值都赋值为 true 。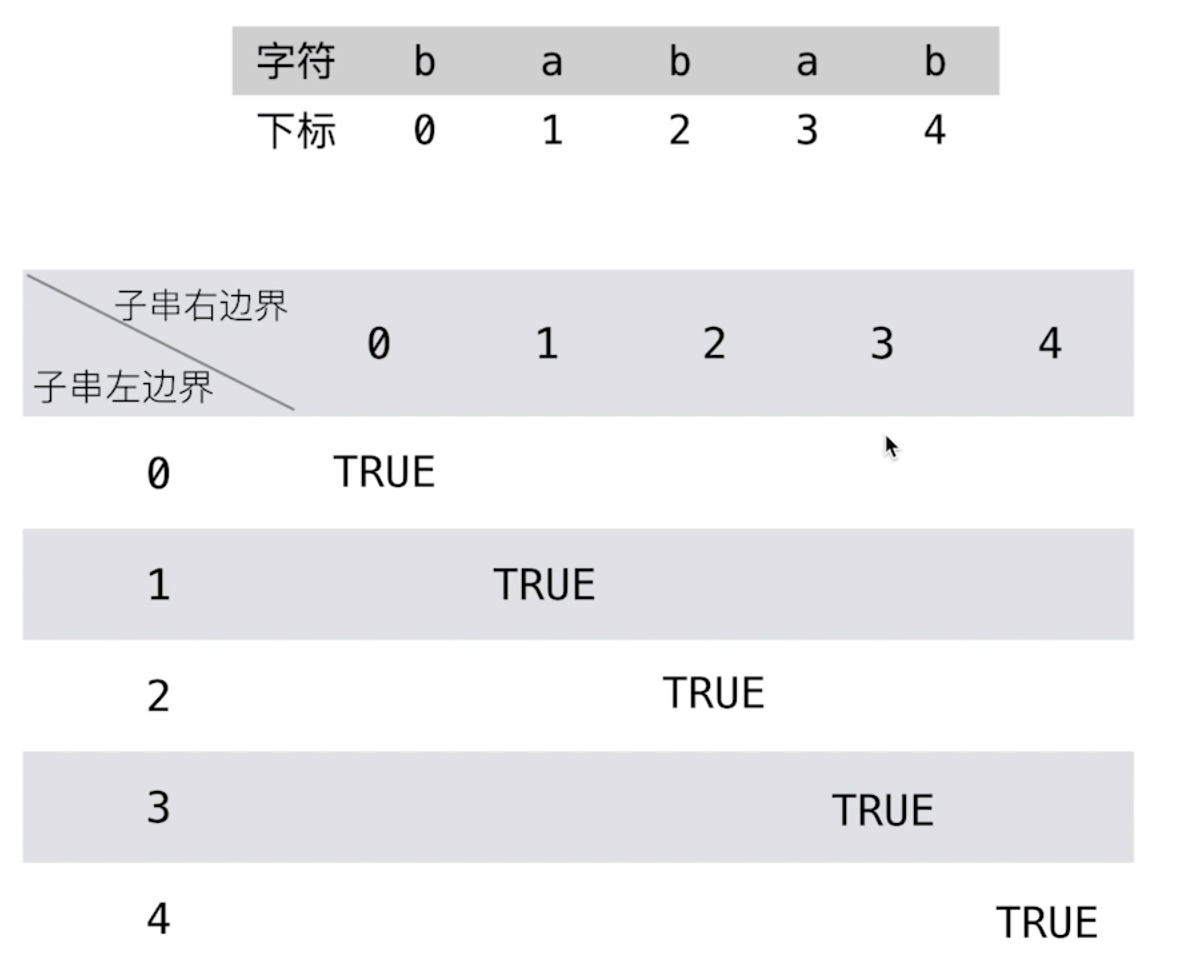
image.png

我们看一下上面得出的状态转移方程：
dp[ i ][ j ] = ( s[ i ]==s[ j ] ) and ( j - i < 3 or dp[ i+1 ][ j-1 ] )

由于 dp[ i ][ j ] 需要参考 dp[ i+1 ][ j-1] 的值，也就是它左下方的值。所以我们在填表的时候就不能一行一行从左向右填写了。
一种参考方案是：一列一列的填写。这样就能保证左下方的值先计算出来，状态转移才会是正确的。

1）先升序填列 2）再升序填行

填表顺序如下图红色数字所示：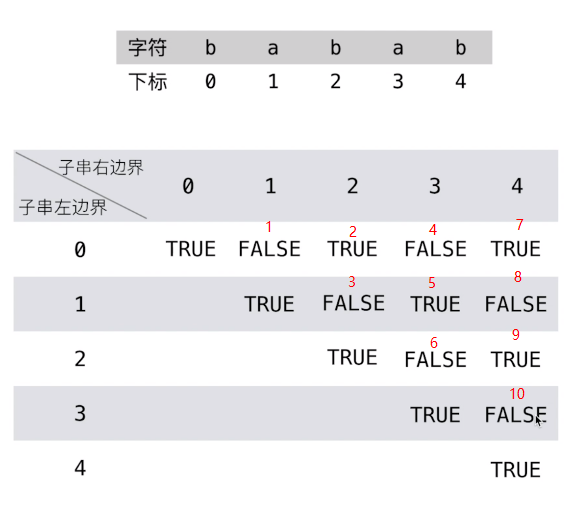
image.png
其中最具有代表性的是 dp[ 0 ][ 4 ] 的值的计算，下标 0 和 4 代表了整个字符串，头和尾相等（ 0=>b ，4=>b），就要参考中间部分是否是回文，也就是由 dp[ 1 ][ 3 ] 决定。

按照这样的规则，我们就可以填完整张表格。

4、Manacher 算法 / 马拉车算法（终极解法）

绝大多数面试和笔试不考查 Manacher 算法。

答案

1、枚举所有的子串

  1. /**
  2.  * 枚举所有子串
  3.  */
  4. class Solution {
  5.     public String longestPalindrome(String s) {
  6.         // 获取字符串长度
  7.         int len = s.length();
  8.         // 特殊情况判断
  9.         if (len < 2) {
  10.             return s;
  11.         }
  13.         //最长回文子串的起始下标与长度
  14.         int begin = 0;
  15.         int maxLen = 1;
  16.         // s.charAt(i) 每次都会检查数组下标越界，因此先转换成字符数组，这一步非必需
  17.         char[] charArray = s.toCharArray();
  19.         // 枚举所有长度严格大于 1 的子串 charArray[i..j]
  20.         for (int i = 0; i < len - 1; i++) {
  21.             for (int j = i + 1; j < len; j++) {
  22.                 // 查看当前遍历到的子串
  23. //                printCharArray(charArray, begin, j - i + 1);
  25.                 // 如果当前子串的长度超过了当前最大回文串的长度，则判断是否为回文串
  26.                 if (j - i + 1 > maxLen && isPalindromic(charArray, i, j)) {
  27.                     // 记录回文串的长度
  28.                     begin = i;
  29.                     maxLen = j - i + 1;
  30.                 }
  31.             }
  32.         }
  34.         return s.substring(begin, begin + maxLen);
  35.     }
  37.     // 验证子串 s[left...right] 是否为回文串
  38.     public boolean isPalindromic(char[] charArray, int left, int right) {
  39.         while (left < right) {
  40.             if (charArray[left] != charArray[right]) {
  41.                 return false;
  42.             }
  43.             left++;
  44.             right--;
  45.         }
  46.         return true;
  47.     }
  49.     // debug 输出指定长度的 char 数组内容
  50.     public void printCharArray(char[] charArray, int begin, int len) {
  51.         String s = "";
  52.         for (int n = begin; n < len; n++) {
  53.             s += charArray[n];
  54.         }
  55.         System.out.println(s);
  56.     }
  57. }

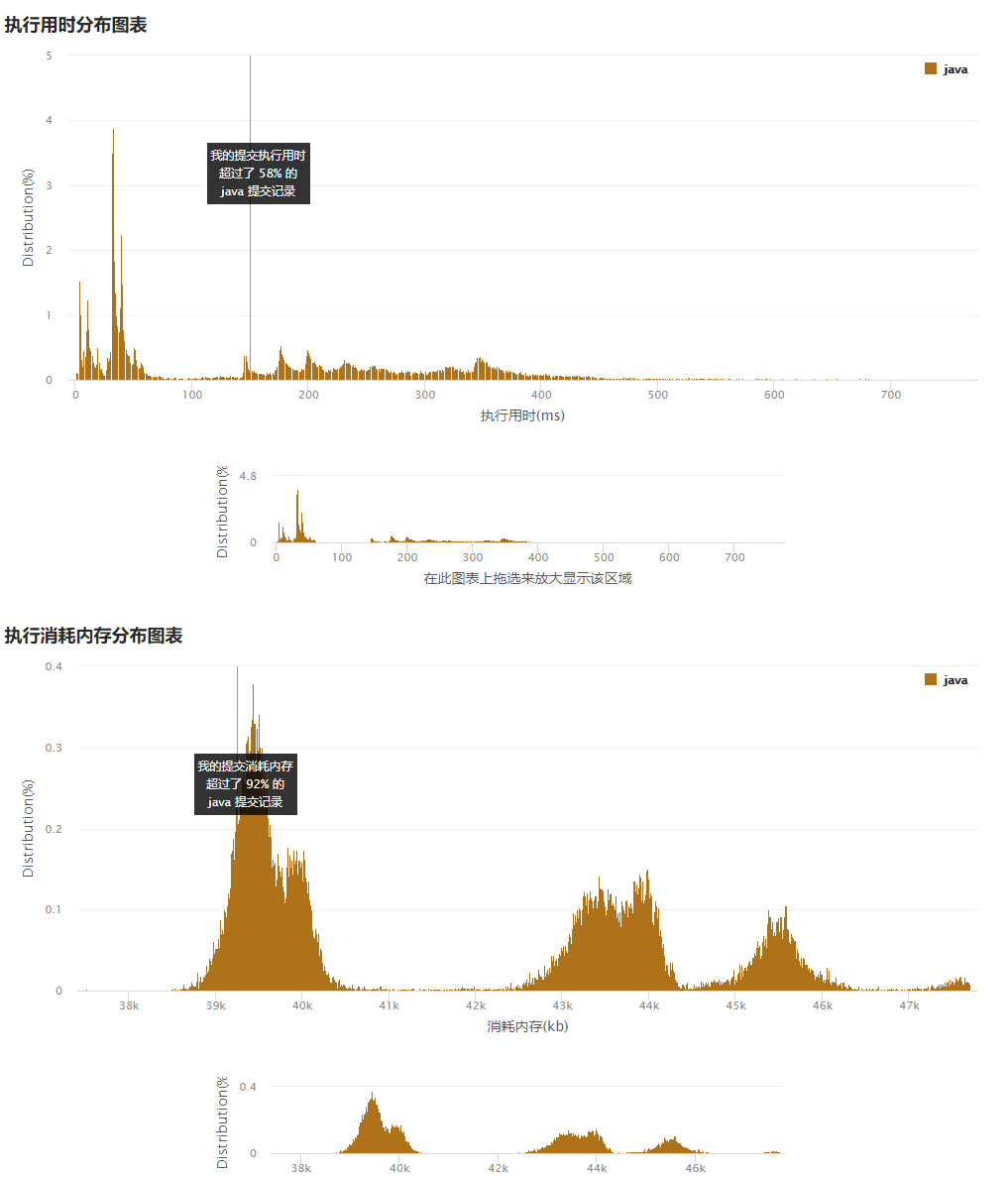
image.png

2、枚举所有可能的回文子串的中心位置

  1. /**
  2.  * 枚举所有回文中心
  3.  */
  4. class Solution {
  5.     public String longestPalindrome(String s) {
  6.         // 获取字符串长度
  7.         int len = s.length();
  8.         // 特殊情况判断
  9.         if (len < 2) {
  10.             return s;
  11.         }
  13.         //最长回文子串的起始下标与长度
  14.         int begin = 0;
  15.         int maxLen = 1;
  16.         // s.charAt(i) 每次都会检查数组下标越界，因此先转换成字符数组，这一步非必需
  17.         char[] charArray = s.toCharArray();
  20.         for (int i = 0; i < len - 1; i++) {
  21.             // 以单个字符为中心扩散
  22.             int oddLen = expandAroundCenter(charArray, i, i);
  23.             // 以两个字符为中心扩散
  24.             int evenLen = expandAroundCenter(charArray, i, i + 1);
  26.             int currentMaxLen = Math.max(oddLen, evenLen);
  27.             if (currentMaxLen > maxLen) {
  28.                 maxLen = currentMaxLen;
  29.                 begin = i - (maxLen - 1) / 2;
  30.             }
  31.         }
  33.         return s.substring(begin, begin + maxLen);
  34.     }
  36.     /**
  37.      * 中心扩展
  38.      *
  39.      * @param charArray 原始字符串的字符数组
  40.      * @param left      起始做边界（可以取到）
  41.      * @param right     起始右边界（可以取到）
  42.      * @return 回文串的长度
  43.      */
  44.     public int expandAroundCenter(char[] charArray, int left, int right) {
  45.         // 当 left = right 时，回文中心是单个字符，回文串的长度是奇数
  46.         // 当 right = left +1 时，此时回文中心是两个字符，回文串的长度是偶数
  47.         int len = charArray.length;
  49.         while (left >= 0 && right < len) {
  50.             if (charArray[left] == charArray[right]) {
  51.                 left--;
  52.                 right++;
  53.             } else {
  54.                 break;
  55.             }
  56.         }
  58.         // 跳出 while 循环时，恰好满足 s.charAt(left)!=s.charAt(right), left 到 right 中间的部分是回文子串，不包括 left 和 right 指向的字符。
  59.         // 回文串的长度是 right - left + 1 - 2 = j - i - 1
  60.         return right - left - 1;
  61.     }
  62. }

image.png

3、动态规划

  1. /**
  2.  * 动态规划
  3.  */
  4. class Solution {
  5.     public String longestPalindrome(String s) {
  6.         // 获取字符串长度
  7.         int len = s.length();
  8.         // 特殊情况判断
  9.         if (len < 2) {
  10.             return s;
  11.         }
  13.         //最长回文子串的起始下标与长度
  14.         int begin = 0;
  15.         int maxLen = 1;
  16.         // s.charAt(i) 每次都会检查数组下标越界，因此先转换成字符数组，这一步非必需
  17.         char[] charArray = s.toCharArray();
  19.         // 动态规划二维表
  20.         // dp[i][j] 表示 s[i..j] 是否是回文
  21.         boolean[][] dp = new boolean[len][len];
  22.         for (int i = 0; i < len; i++) {
  23.             // 主对角线上的值先赋值为 true
  24.             dp[i][i] = true;
  25.         }
  27.         // 左下角先填
  28.         for (int j = 1; j < len; j++) {
  29.             for (int i = 0; i < j; i++) {
  30.                 // 当前填写的表格坐标
  31. //                System.out.println("dp[" + i + "]" + "[" + j + "]");
  33.                 if (charArray[i] != charArray[j]) {
  34.                     // 首尾不相等，直接赋值为 false
  35.                     dp[i][j] = false;
  36.                 } else {
  37.                     // 如果 j - 1 - ( i + 1 ) +1 < 2 不构成区间
  38.                     if (j - i < 3) {
  39.                         dp[i][j] = true;
  40.                     } else {
  41.                         dp[i][j] = dp[i + 1][j - 1];
  42.                     }
  43.                 }
  45.                 // 只要 dp[i][j] == true 成立，就表示子串 s[i..j] 是回文，此时记录回文长度和起始位置
  46.                 if (dp[i][j] == true && j - i + 1 > maxLen) {
  47.                     maxLen = j - i + 1;
  48.                     begin = i;
  49.                 }
  50.             }
  51.         }
  53.         return s.substring(begin, begin + maxLen);
  54.     }
  56.     /**
  57.      * 中心扩展
  58.      *
  59.      * @param charArray 原始字符串的字符数组
  60.      * @param left      起始做边界（可以取到）
  61.      * @param right     起始右边界（可以取到）
  62.      * @return 回文串的长度
  63.      */
  64.     public int expandAroundCenter(char[] charArray, int left, int right) {
  65.         // 当 left = right 时，回文中心是单个字符，回文串的长度是奇数
  66.         // 当 right = left +1 时，此时回文中心是两个字符，回文串的长度是偶数
  67.         int len = charArray.length;
  69.         while (left >= 0 && right < len) {
  70.             if (charArray[left] == charArray[right]) {
  71.                 left--;
  72.                 right++;
  73.             } else {
  74.                 break;
  75.             }
  76.         }
  78.         // 跳出 while 循环时，恰好满足 s.charAt(left)!=s.charAt(right), left 到 right 中间的部分是回文子串，不包括 left 和 right 指向的字符。
  79.         // 回文串的长度是 right - left + 1 - 2 = j - i - 1
  80.         return right - left - 1;
  81.     }
  82. }

image.png